1.
Introduction
Catalan's conjecture, one of the famous classical problems in number theory, states that the equation
has no solutions in positive integers x and y, other than 32−23=1, where p and q are prime numbers. In 2004, Mihuailesc [1] proved Catalan's conjecture by using the theory of cyclotomic field. On the other hand, some scholars (see [2], and [3,4,5]) studied the solutions to the general equation
where a,b and c are fixed positive integers. In 1936, Pillai conjectured that the number of positive integer solutions (a,b,x,y), with x≥2,y≥2, to Eq (1.1) is finite. This conjecture which is still open for all c>1, amounts to saying that the distance between two consecutive terms in the sequence of all perfect powers tends to infinity. However, it is easy to see that Pillai's conjecture is closely related to the number of consecutive integers tuples of perfect powers. In fact, Catalan's conjecture is equivalent to the statement that no two consecutive integers are perfect powers, other than 23 and 32. We also easily know that there are no four consecutive integers with each of them being perfect powers, since any set of four consecutive integers must contain one integer of the form 4n+2 which can not be a perfect power. Are there three consecutive integers with each of them being perfect powers? In 1962, Chao Ko [6], by supplying a sufficient and necessary condition for the equation xp−yq=1 to be solvable with positive integers x and y, showed that no three consecutive integers are powers of other positive integers,
Let k be an integer with k≥2. In this paper, let us turn our attention to the number of k tuples of consecutive integers such that each of them is the sum of two perfect powers. For any positive integer n, we call the integer n a 22-STP (STP means Sum of Two Powers) number if it can be expressed in the form 2x+y2 with x and y being nonnegative integers. Furthermore, we call a k-tuple (a1,a2,⋯,ak) nice if a1,a2,⋯,ak are increasingly consecutive integers and each of them is a 22-STP number. Then an interesting question is raised naturally as follows.
Question 1.1. For each integer k≥2, how many nice k-tuples are there?
In this paper, we mainly study Question 1.1 by utilizing some elementary tools in number theory. In fact, we provide the following theorem, which gives the complete answer to Question 1.1.
Theorem 1.2. Let k be an integer with k≥2. Each of the following is true.
(a) If 2≤k≤4, then there exist infinitely many nice k-tuples.
(b) If k=5, then there are only six nice 5-tuples. Moreover, the only six nice 5-tuples can be listed as follows:
(c) If k=6, then there are only three nice 6-tuples. Moreover, the only three nice 6-tuples can be list as follows:
(d) If k≥7, then there is no nice k-tuple at all.
This paper is organized as follows. First in Section 2, we are mainly dedicated in presenting the proof of Theorem 1.2 by using the method of elementary number theory, especially the tool of modulo cover. In Section 3, we propose a general question for readers who are interested in this topic to do further.
2.
Proof of Theorem 1.2
In this section, we are concentration on the proof of Theorem 1.2.
Proof of Theorem 1.2. First of all, it is noticed that Parts (c) and (d) of Theorem 1.2 follows immediately from Part (b). So it is sufficient to show that Parts (a) and (b) are true.
For Part (a), we only need to prove that there exist infinitely nice 4-tuples, since from which one can easily deduce that Part (a) holds for any k∈{2,3}. One notes that the integers y2+20,y2+21,y2+22 are 22-STP numbers for every nonnegative integer y. So the proof of Part (a) will be done if we show that y2+3 is 22-STP finitely often. Now let us consider the diophantine equation y2+3=2x+y′2. We claim that this equation at least has one solution (y,y′)∈N2 for any x∈N≥2. In fact, since
then one can take y−y′=1 and y+y′=2x−3, that is, (y,y′)=(2x−1−1,2x−1−2)∈N2. Thus, this completes the proof of Part (a).
Now we turn our attention to Part (b). First, we make a key table as follows to show the results of 2x+y2(mod8).
One knows from the key table that there is no 22-STP number which is congruent to 7 modulo 8. It then follows that any nice 5-tuple must contain an integer with 3(mod8). Let this integer be denoted by A. Thus by the key table we know that A=y20+2 for some odd positive integer y0. So we can list all possible nice 5-tuples containing A=y20+2 as follows:
(ⅰ) (y20+1,y20+2,y20+3,y20+4,y20+5),
(ⅱ) or (y20,y20+1,y20+2,y20+3,y20+4),
(ⅲ) or (y20−1,y20,y20+1,y20+2,y20+3),
since y20+2≡3(mod8) and any number in all possible nice 5-tuples is not congruent to 7 modulo 8. Next, let's discuss the details case by case.
CASE 1. Suppose the nice 5-tuple is (y20+1,y20+2,y20+3,y20+4,y20+5). Note that y20+2≡3(mod8), then y20+5≡6(mod8). It follows from the key table that there exists a positive integer z with z≡2(mod4) such that y20+5=z2+2. So one has that (z+y0)(z−y0)=3, which implies that z+y0=3,z−y0=1, i.e., z=2,y0=1. It gives the unique nice 5-tuple (2,3,4,5,6) of this case since that 2=20+12,3=21+12,4=22+02,5=22+12,6=21+22.
CASE 2. Suppose the nice 5-tuple is (y20,y20+1,y20+2,y20+3,y20+4). First, since y20 is a 22-STP number, then there exist two nonnegative integers s and u such that y20=2s+u2, which one writes as
Now we solve Eq (2.1) by dividing s into two subcases.
SUBCASE 2.1. Let 0≤s≤4.
● If s=0, then y0=1 and u=0, which gives a nice 5-tuple (1,2,3,4,5) since 1=20+02.
● If s=1, then it is easy to see that Eq (2.1) has no no integer solution since y0+u and y0−u have the same parity.
● If s=2, then Eq (2.1) is equivalent to the equations y0+u=2 and y0−u=2 since y0+u and y0−u have the same parity, which gives y0=2, a contradiction with y0 being odd.
● If s=3, then Eq (2.1) implies that y0+u=4 and y0−u=2 since y0+u and y0−u have the same parity. So y0=3. It gives a nice 5-tuple (9,10,11,12,13) since 9=23+12,10=20+32,11=21+32,12=23+22,13=22+32.
●If s=4, then from Eq (2.1), we have that y0+u=4 and y0−u=4, or y0+u=8 and y0−u=2 since y0+u and y0−u have the same parity. So y0=4 or 5. Note that y0 was odd, then y0=5, which gives a possible nice 5-tuple (25,26,27,28,29). But it is easy to check that 28 is not a 22-STP integer. So the 5-tuple (25,26,27,28,29) is not nice.
SUBCASE 2.2. Suppose s≥5. First, one notes that gcd(y0+u,y0−u)∣2y0 and y0 is odd. Then, by (2.1) we have that y0−u=2,y0−u=2s−1, which implies that y0=2s−2+1. Let's now focus on the 22-STP number y20+3. One can write that
for some two nonnegative integers t and w. Now we discuss the details for t by splitting into following cases.
SUBCASE 2.2.1. Assume 0≤t≤2.
★ If t=0, we then easily find that Eq (2.2) has no integer solution.
★ If t=1, then Eq (2.2) can be reduced to that y0=1 and w=1, a contradiction, since y0 was odd.
★ If t=2, then Eq (2.2) is equivalent to that y0+w=1 and y0−w=1, i.e., y0=1,w=0. This gives the nice 5-tuple (1,2,3,4,5) which was obtained in Subcase 2.1.
SUBCASE 2.2.2. Assume t≥3. Note that y0=2s−2+1 with s≥5. By substituting y0=2s−2+1 into (2.2), we have that
It yields that w≡2(mod4) since s≥5 and t≥3. In (2.3), for simplicity, let s−3=c≥2,t−2=a≥1,b=w2, then (2.3) becomes that
It then follows that
which implies that b≤2c. So
Then 2a>2c, i.e., a>c. Thus we rewrite (2.4) as
However, one notes that gcd(2c+1−b,2c+1+b)∣2b and b is odd. Then we deduce that one of 2c+1−b and 2c+1+b has at most one factor of 2. By (2.5), we then know that 2c−1 divides one of 2c+1−b and 2c+1+b. Hence b≡±1(mod2c−1). This together with 1≤b≤2c gives that b∈{1,2c−1−1,2c−1+1,2c−1}.
★ If b=1, then Eq (2.4) is equivalent to the equation 2c+1=2a−c which has no integer solution since c≥2 and a>c.
★ If b=2c−1−1, then Eq (2.4) turns out to be 3×2c−2=2a−c−2. It then follows that a−c=3 and c−2=1, i.e., c=3 or s=6. So y0=2s−2+1=17. This gives us a new nice 5-tuple (289,290,291,292,293) since 289=26+152,290=20+172,291=21+172,292=28+62,293=23+172.
★ If b=2c−1+1, then Eq (2.4) is simplified to that 2c−1+2c−2=2a−c. Clearly, the later equation has no integer solution.
★ If b=2c−1, then Eq (2.4) is reduced to be 2c+1=2c(2a−c+1), a contradiction.
CASE 3. Suppose the nice 5-tuple is (y20−1,y20,y20+1,y20+2,y20+3). Then (y20,y20+1,y20+2,y20+3,y20+4) is also a nice 5-tuple since y20+4=y20+22. It then follows from Case 2 that y0∈{1,3,5,17}. But one checks that (y20−1,y20,y20+1,y20+2,y20+3) can not be a nice 5-tuple for each y0∈{1,5} since both 0 and 28 are not 22-STP integers. But y0=3 or 17 give the new nice 5-tuples (8,9,10,11,12) and (288,289,290,291,292), as 8=22+22 and 288=25+162.
Hence, the above cases give the all nice 5-tuples, which are (1,2,3,4,5),(2,3,4,5,6), (8,9,10,11,12),(9,10,11,12,13),(288,289,290,291,292),(289,290,291,292,293).
To here, the proof of Part (b) is complete.
Thus we finish the proof of Theorem 2.2.
3.
A general question
In this section, we will propose one general question. Let a,b be given integers with a,b≥2. Let n be a positive integer. We call the integer n an ab-STP number if it can be expressed in the form ax+yb with x and y being nonnegative integers. Furthermore, we call a k-tuple (a1,a2,⋯,ak) ab-nice if a1,a2,⋯,ak are increasingly consecutive integers and each of them is an ab-STP number. Now we propose the following general question which seems little hard, as follows.
Question 3.1. Let a and b be given integers with a,b≥2. For each integer k≥2, find all ab-nice k-tuples.
4.
Conclusions
The gap in integer sequences are wide problems in Number Theory. The gap of primes |pn−pn+1| is one of the most important topics in analytic Number Theory. In the field of Diophantine analysis, there are many open questions on the gap of the powers |xm−yn|. In this paper, we considered k-tuples of consecutive integers (a1,a2,⋯,ak) such that each of them is the sum of two perfect powers. We used some elementary methods in number theory to prove that there exists infinitely many 4-tuples with each elements of the form 2x+y2, no such 7-tuples exists, and such quintuples and sextuples were listed. At the end of this paper, a general question was also proposed for the interested readers there.
Acknowledgments
The authors would like to thank the referees for their helpful comments. This work was supported partially by China Scholarship Council Foundation # 201908510050 and the Research Initiation Fund for Young Teachers of China West Normal University # 412679.
Conflict of interest
The authors declare that there is no conflict of interest.









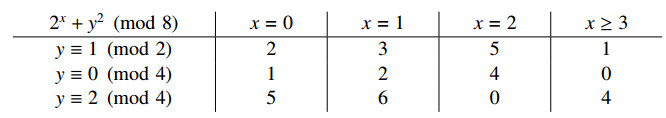






 DownLoad:
DownLoad: