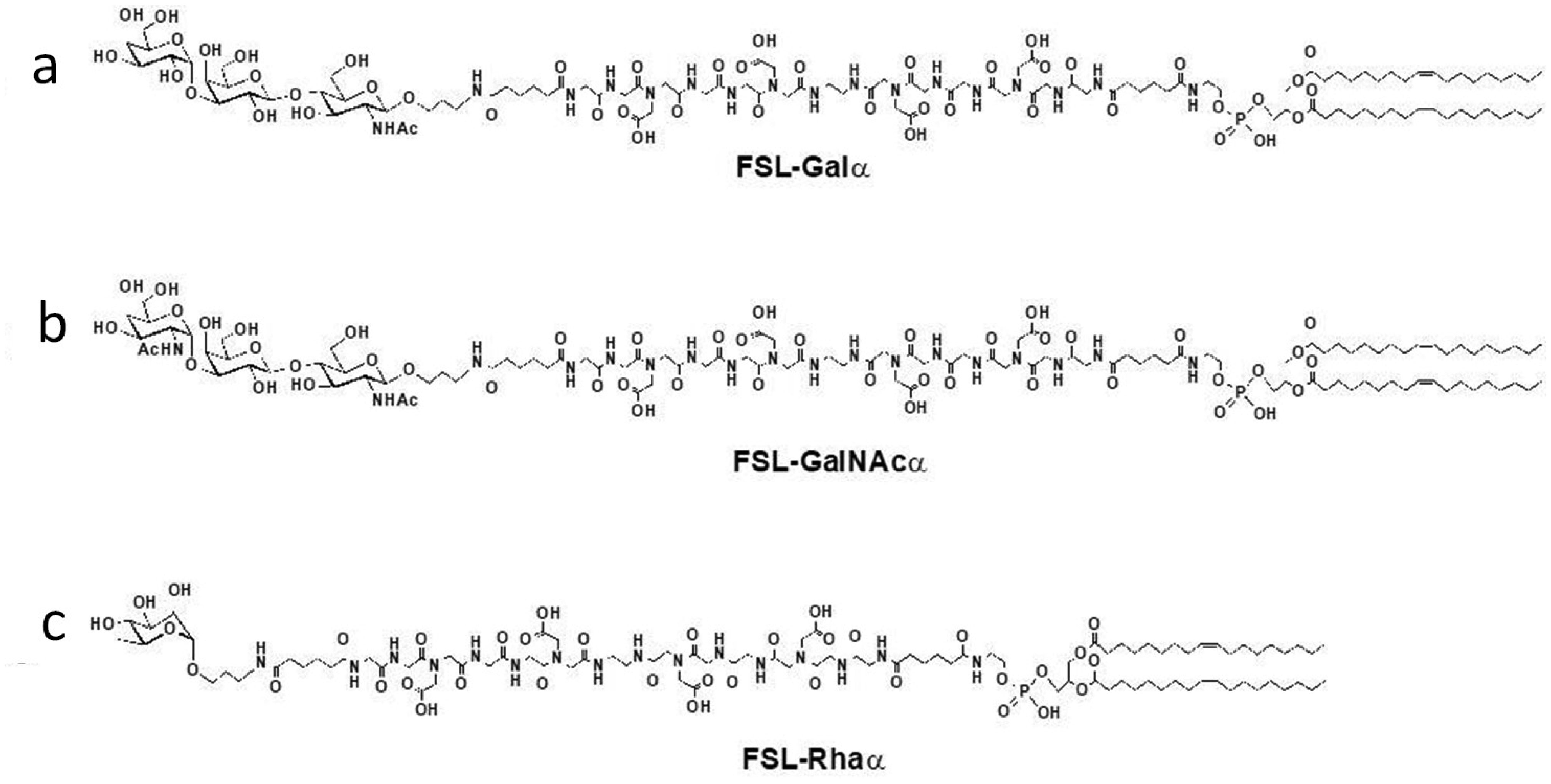
Antibodies against xeno-glycan antigens terminating with the saccharides Galα, GalNAcα and Rhaα are ubiquitous in human blood. Although originating as barriers to infection some of these naturally occurring complement-activating antibodies also contribute to disease processes, hinder xenotransplantation and have potential medical roles in immuno-oncotherapy. Because concentration of antibody is important in determining biological activity, there is a need to understand population variation in naturally occurring antibody levels, and to be able to rapidly and accurately determine levels in individuals. Xeno-glycan antigens in the form of function-spacer-lipid constructs were used to modify human red cells (kodecytes) to have on their surface micromolar equivalents of the xeno-glycan antigens Galα1-3Galβ1-4GlcNAc, GalNAcα1-3Galβ1-4GlcNAc and Rhaα. The methodology used was based on a previously validated kodecyte method used for quantifying IgM and IgG ABO human blood group antibodies in undiluted plasma. We tested plasma samples from 100 healthy individuals against these three different xeno-glycan kodecytes with each at three different loading concentrations of antigen to determine relative levels of these antibodies in human plasma. Sixty-one samples were also independently tested by enzyme immunoassay to correlate levels of anti-Galα. Results demonstrate independence between antibody specificities and substantial variation between individuals in levels of these antibodies, with >92% of the population having medium or high levels of at least one specificity. However, of particular importance was that 5–8% of the population had low levels of both IgM and IgG to at least one specificity and these individuals would probably have a poor immediate response when challenged by the corresponding antigen.
1.
Introduction
In recent years, more and more researchers are interested in the discontinuous differential operators for its wide application in physics and engineering (see [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]). Such problems are connected with discontinuous material properties, such as heat and mass transfer which can be found in [10], vibrating string problems when the string loaded additionally with point masses, the heat transfer problems of the laminated plate of membrane (that is, the plate which is formed by overlap of materials with different characteristics) and diffraction problems, etc. Lots of important results in this field have been obtained for the case when the eigenparameter appears not only in the differential equation but also in the boundary conditions. Particularly, more and more researchers have paid close attention to Sturm-Liouville problems with the boundary condition depending on eigenparameter and its inverse problem, asymptotic of eigenvalues and eigenfunctions, oscillation theory, etc. The various physics applications of this kind of problem are found in many literature, such as Hinton[17], Fulton[16], Binding [22]. While the general theory and methods of such second-order boundary value problems are highly developed (see[6,7,8,9,10,11,12,13,14,15,16,17], [21,22,23,24,25,26,27,28,29,30]), little is known about a general characteristic of the high-order problems, and the case of fourth-order is also very little[31,32].
Yang and Wang studied a class of fourth order differential operators with transmission conditions and containing eigenparameter in the boundary conditions at one endpoint (see[19]), and obtained Green function, asymptotic formulas of eigenvalues and the completeness of eigenfunctions. In [20], Erdoǧan Ṣen studied spectral properties of a fourth order differential operators with transmission conditions and containing eigenparameter in the boundary conditions at one endpoint, the completeness of eigenfunctions and the asymptotic formulas of eigenvalues and fundamental solutions are discussed.
In this paper, we shall consider the following fourth-order boundary value transmission problems
with eigenparameter dependent boundary conditions at endpoints
and transmission conditions at discontinuous point x=0
where p(x)=p41 for x∈[−1,0), p(x)=p42 for x∈(0,1]; ω(x)=ω41 for x∈[−1,0), ω(x)=ω42 for x∈(0,1], pi>0 and ωi>0 are given real numbers (i=1,2). The real-valued function q(x)∈L1[J,R], λ∈C is a complex eigenparameter, γi,γ′i,(i=1,2,3,4) are real numbers, Bu(x)=(u(x),u′(x),u″(x),u‴(x))T.
is a 4×4 real matrix,
We assume that ρ0=|δ1α2δ4β4| = |α3α4β1β2|>0, ρ1=|γ′1γ1γ′2γ2|>0,ρ2=|γ′3γ3γ′4γ4|>0, ρ3=|α1α2β3β4|=|δ2α4δ3β2|=0, ρ4=|δ1α1δ4β3| = |δ2α3δ3β1|>0.
In order to investigate the problems (1.1)–(1.6), we define the inner product in L2(J) as
where
It is easy to verify that H1=L2(J,⟨⋅,⋅⟩1) is a Hilbert space.
Here we consider a class of fourth order differential operators with discontinuous coefficient and containing eigenparameter in the boundary conditions at two endpoints. By using the classical analysis techniques and spectral theory of linear operator, a new linear operator A associated with the problem in an appropriate Hilbert space H is defined such that the eigenvalues of the problem coincide with those of A. The main results of the present paper are to discuss its eigenvalues, obtain asymptotic formulas for fundamental solutions and characteristic function, prove that the eigenfunctions of A are complete in H, and give its Green function, which promote and deepen the previous conclusions.
The rest of this paper is organized as follows: In Section 2, we define a new self-adjoint operator A such that the eigenvalues of such a problem coincide with those of A. In Section 3, we construct its fundamental solutions, discuss some properties of eigenvalues. In Section 4, we get the asymptotic formulas for the fundamental solutions and the characteristic function. The completeness of eigenfunctions are discussed in Section 5. In Section 6, we constructed its Green function.
2.
Operator formulation
In this section, we introduce a special inner product in the Hilbert space H=H1⨁C4, where H1=L2[−1,0)⨁L2(0,−1] (for any interval I⊂R, L2(I) denotes all the complex valued functions which satisfy ∫I|f(x)|2dx<∞), C4 denotes the Hilbert space of complex numbers, a symmetric operator A defined on the Hilbert space such that (1.1)–(1.6) can be considered as the eigenvalue problem of this operator. Namely, we define an inner product on H by
for F:=(f(x),h1,h2,h3,h4), G:=(g(x),k1,k2,k3,k4)∈H, where ⟨h,k⟩2=h¯k for h,k∈C.
For convenience, we shall use the following notations:
In the Hilbert space H, we consider the operator A with domain
and the rule
with
Now we rewrite the problems (1.1)–(1.6) in the operator form
Thus the problems (1.1)–(1.6) can be considered as the eigenvalue problem of the operator A.
Lemma 2.1. The eigenvalues and the eigenfunctions of the problems (1.1)–(1.6) are defined as the eigenvalues and the first component of corresponding eigenelements of the operator A respectively.
Lemma 2.2. The domain D(A) is dense in H.
Proof. Let F=(f(x),h1,h2,h3,h4)∈H, F⊥D(A) and C∞0 be a functional set such that
for φ1(x)∈C∞0[−1,0), φ2(x)∈C∞0(0,1]. Since C∞0⊕0⊕0⊕0⊕0⊂D(A) (0∈C), any U=(u(x),0,0,0,0)∈C∞0⊕0⊕0⊕0⊕0 is orthogonal to F, namely,
We can learn that f(x) is orthogonal to C∞0 in H1, this implies f(x)=0. So for all V=(v(x),M′1(v),0,0,0)∈D(A), ⟨F,V⟩=ρ0h1M′1(¯v)=0. Thus h1=0 since M′1(v) can be chosen as an arbitrary function. Similarly, we can prove h2=h3=h4=0. Hence F=(0,0,0,0,0,) is null element in the Hilbert space H. Thus, the orthogonal complement of D(A) consists of only the null element, and therefore is dense in the Hilbert space H.
Theorem 2.1. The operator A is self-adjoint in H.
Proof. Let F,G∈D(A). Integration by parts yields
where, as usual, W(f,g;x) denotes the Wronskians of f and g:
By the transmission condition (1.6), we get
Further, it is easy to verify that
Now, substituting (2.4)–(2.6) into (2.2) yields that
Hence A is symmetric.
It remains to show that if ⟨AF,W⟩=⟨F,U⟩ for all F=(f(x),M′1(f),M′1(f),N′1(f),N′2(f))∈D(A), then W∈D(A) and AW=U, where W=(w(x),h1,h2,h3,h4), U=(u(x),k1,k2,k3,k4), i.e.,
(i) w(i)1(x)∈ACloc((−1,0)), w(i)2(x)∈ACloc((0,1)) (i=0,1,2,3), lw∈H1;
(ii) h1=M′1(w)=w(−1), h2=M′2(w)=w′(−1), h3=N′1(w)=γ′1w(1)−γ′2w‴(1),
h4=N′2(w)=γ′3w′(1)−γ′4w″(1);
(iii) Bw(0+)=B⋅Bw(0−);
(iv) u(x)=lw;
(v) k1=M1(w)=w‴(−1), k2=−M2(w)=−w″(−1), k3=N1(w)=γ1w(1)−γ2w‴(1),
k4=−N′2(w)=−(γ3w′(1)−γ4w″(1)).
For an arbitrary point F∈C∞0⊕04∈D(A) such that
that is, ⟨lf,w⟩1=⟨f,u⟩1. According to classical Sturm-Liouville theory, (i) and (iv) hold. By (iv), equation ⟨AF,W⟩=⟨F,U⟩, ∀F∈D(A), becomes
However,
So
By Naimark Patching Lemma 2, there is an F∈D(A) such that
For such an F,
Then from (2.7) we have
On the one hand,
On the other hand,
So h3=N′1(w). Similarly, we can prove that h4=N′2(w), k3=N1(w), k4=−N2(w).
For an arbitrary F∈D(A) such that
For such an F,
Then from (2.7) we have
On the one hand,
On the other hand,
So h2=M′2(¯w). Similarly, we can proof h1=M′1(w), k1=M1(w), k2=−M2(w). So (ii) and (v) hold.
Next choose F∈D(A) such that
thus Mi(f)=M′i(f)=Ni(f)=N′i(f)=0 (i=1,2), W(f,¯g;−1)=W(f,¯g;1)=0. Then from (3.1) we have W(f,¯g;0+)=ρ0W(f,¯g;0−), that is
so
However, B is a 4×4 real matrix, then using the same method, we can prove
So (iii) holds.
From the above discussion, we get that A is a self-adjoint operator.
Corollary 2.1. All eigenvalues of the problems (1.1)–(1.6) are real.
Corollary 2.2. Let λ1 and λ2 be two different eigenvalues of the problems (1)–(6). Then the corresponding eigenfunctions f and g is orthogonal in the sense that
Since all eigenvalues are real, it is necessary to study the real-valued eigenfunctions only. Therefore, we can now assume that all eigenfunctions are real-valued.
3.
Fundamental solutions
Lemma 3.1. Let the real-valued function q(x) be continuous in [−1,1] and fi(λ) (i=1,2,3,4) be given entire functions. Then for ∀λ∈C, the Eq (1.1) has a unique solution u(x,λ), satisfying the initial conditions
Proof. In terms of existence and uniqueness in ordinary differential equation theory, we can conclude this conclusion.
Let ϕ11(x,λ) be the solution of Eq (1.1) on the interval [−1,0), satisfying the initial conditions
By virtue of Lemma 3.1, after defining this solution we can define the solution ϕ12(x,λ) of Eq (1.1) on the interval (0, 1] by the initial conditions
Again let ϕ21(x,λ) still be the solution of (1.1) on the interval [−1,0), satisfying the initial conditions
After defining this solution, we can also define the solution ϕ22(x,λ) of Eq (1.1) on the interval (0, 1] by the initial conditions
Analogously, we shall define the solutions χ12(x,λ) and χ11(x,λ) by the initial conditions
where
is a 4×4 real matrix.
In addition, we shall define the solution χ22(x,λ) and χ21(x,λ), satisfying the initial conditions
Let us consider the Wronskians
and
which are independent of x and are entire functions. Short calculation gives W2(λ)=ρ20W1(λ). Now we may introduce, in consideration, the characteristic function as W(λ)=W1(λ).
Theorem 3.1. The eigenvalues of the problems (1.1)–(1.6) consist of the zeros of the function W(λ).
Proof. Assume that W(λ)=0. Then the functions ϕ11(x,λ), ϕ21(x,λ) and χ11(x,λ), χ21(x,λ) are linearly dependent, i.e.,
for some k1≠0 or k2≠0 and k3≠0 or k4≠0. From this, it follows that k3χ11(x,λ)+k4χ21(x,λ) satisfies the boundary conditions (1.2) and (1.3). Therefore,
is an eigenfunction of the problems (1.1)–(1.6) corresponding to the eigenvalue λ.
Now we let u(x) be any eigenfunction corresponding to eigenvalue λ, but W(λ)≠0. Then the function u(x) may be represented in the form
where at least one of the constants ci (i=1,2,⋯,8) is not zero. Applying the transmission condition (1.6) and the boundary conditions (1.2)–(1.5) to this representation of u(x), we can get a homogenous system of linear equations of the variables ci (i=1,2,⋯,8) and taking into account the initial conditions, it follows that the determinant of this system is
Therefore, the system has only the trivial solution ci=0(i=1,2,⋯,8). Thus we get a contradiction, which completes the proof.
4.
Asymptotic formulae for the fundamental solutions
In this section, we start by proving several lemmas.
Lemma 4.1. Let λ=s4, s=σ+it. Then the following integral equations hold for k=0,1,2,3,
Proof. Regarding ϕ11(x,λ) as the solution of the following non-homogeneous Cauchy problem:
Using the method of constant variation, ϕ11(x,λ) satisfies
Then differentiating it with respect to x, we have (4.1). The proof for (4.2)–(4.4) are similar.
Lemma 4.2. Let λ=s4, s=σ+it. Then the following integral equations hold for k=0,1,2,3,
Each of these asymptotic equalities hold uniformly for x∈J, as |λ|→∞.
Proof. Let ϕ11(x,λ)=|s|e|s|ω1(x+1)p1F(x,λ). We can easily get that F(x,λ) is bounded. So ϕ11(x,λ)=O(|s|e|s|ω1(x+1)p1). Substituting it into (4.1) and differentiating it with respect to x for k=0,1,2,3, we obtain (4.5). Next according to transmission condition (1.6), we have
as |λ|→∞. Substituting these asymptotic expressions into (4.2) for k=0, we get
Multiplying through by |s|−4e|s|[ω1p1+ω2xp2], and denoting
Denoting M(λ):=maxx∈[−1,0)|F12(x,λ)|, from the last formula, short calculation yields M(λ)<M0 for some M0>0. It follows that M(λ)=O(1) as |λ|→∞, so
Substituting this back into the integral on (4.9) yields (4.6) for k=0. The other assertions can be proved similarly.
Theorem 4.1. Let λ=s4, s=σ+it. Then the characteristic function W(λ) has the following asymptotic representations:
Case 1. γ′2≠0, γ′4≠0,
Case 2. γ′2≠0, γ′4=0,
Case 3. γ′2=0, γ′4≠0,
Case 4. γ′2=0, γ′4=0,
Proof. The proof is obtained by substituting asymptotic equalities dkdxkϕ12(1,λ) and dkdxkϕ22(1,λ) into the representation
short calculation, we can get the above conclusions.
Corollary 4.1. The eigenvalues of the problems (1)–(6) are bounded below.
Proof. Putting s2=it (t>0) in the above formulae, it follows that W(−t2)→∞ as t→∞. Hence W(λ)≠0 for λ negative and sufficiently large in modulus.
5.
Completeness of eigenfunction
Theorem 5.1. The operator A has only point spectrum, i.e., σ(A)=σp(A).
Proof. It suffices to prove that if λ is not an eigenvalue of A, then λ∈ρ(A). Here we investigate the equation (A−λ)Y=F∈H, where λ∈R, F=(f(x),h1,h2,h3,h4). Consider the initial-value problem
and the system of equations
Let
be the solution of the equation ly−λω(x)y(x)=0 satisfying the transmission condition (1.6). Let
be a special solution of (5.1). Then (5.1) has general solution in the form
where d∈C.
Since γ is not an eigenvalue of (1.1)–(1.6), we have
or
or
or
The second, third, fourth, and fifth components of the equation (A−λ)Y=F involves the Eq (5.2), so substituting (5.3) into (5.2), and we get
In view of (5.4)–(5.7), we know that d is a unique solution. Thus if λ is not an eigenvalue of (1.1)–(1.6), d is uniquely solvable. Hence y is uniquely determined.
The above arguments show that (A−λI)−1 is defined on all of H. We get that (A−λI)−1 is bounded by Theorem 2.1 and the Closed Graph Theorem. Thus λ∈ρ(A). Hence σ(A)=σp(A).
Lemma 5.1. The eigenvalues of the boundary value problems (1.1)–(1.6) are bounded below, and form a finite or infinite sequence without finite accumulation point.
Proof. By the Corollary 4.1, we know that the eigenvalues of boundary value problems (1)–(6) are bounded below. By Theorem 3.1, we obtain that the zeros of the entire function W(λ) are the eigenvalues of A. And all the eigenvalues of A are real by the self-adjointness of A, that is to say, for any λ∈C with its imaginary part not vanishing, then W(λ)≠0. Therefore, by the distribution of zeros of entire functions, the conclusion holds.
Lemma 5.2. The operator A has compact resolvents, i.e., for each δ∈R/σp(A), (A−δI)−1 is compact on H.
Proof. Let {λ1,λ2,⋯} be the eigenvalues of (A−δI)−1, and let {P1,P2,⋯} be the finite rank orthogonal projection on the corresponding eigensubspace. Since {λ1,λ2,⋯} is a bounded sequence and Pn are mutual orthogonality, ∑∞n=1λnPn is strong convergence to (A−δI)−1, that is, ∑∞n=1λnPn=(A−δI)−1. In light of the number of |λn|>α for any α>0 is finite and Pn are finite rank, we have that (A−δI)−1 is compact.
By the above Lemmas and the spectral theorem for compact operator, we obtain the following theorem:
Theorem 5.2. The eigenfunctions of the problems (1.1)–(1.6), augmented to become eigenfunctions of A, are complete in H, i.e., if we let {Φn=(ϕn(x),M′1(ϕn),M′2(ϕn),N′1(ϕn),N′2(ϕn));n∈N} be a maximum set of orthonormal eigenfunctions of A, where {ϕn(x);n∈N} are eigenfunctions of the problems (1.1)–(1.6), then for all F∈H, F=∑∞n=1⟨F,Φn⟩Φn.
6.
Green function
In this section, we will find the Green function defined by (1.1)–(1.6). For convenience, we assume that p(x)≡1, ω(x)≡1. Let λ not be an eigenvalue of A, we consider the operator equation (λI−A)U=F, F=(f,h1,h2,h3,h4). This operator equation is equivalent to the inhomogeneous differential equation
for x∈J, subject to the inhomogeneous boundary conditions
and transmission condition (1.6).
By applying the standard method of variation of constants, we search the general solution of the non-homogeneous differential equation (6.1) in the form
By using the same techniques as in [2], the general solution of the non-homogeneous differential equation (6.1) are obtained as
where
,
c1,c2⋅⋅⋅c8 are arbitrary constants. Substituting Eqs (6.8) and (6.9) into transmission condition (1.6), we obtain
Meanwhile,
By the initial conditions, we get
So we can rewrite in the form
where
Substituting (6.10) into (6.9), we have
We can rewrite in the form
where
Obviously, the solution for Eq (31) can be represented in the form:
with
Denoting
Substituting into the above conditions, we have
As the determinant of this system is not zero, so the variables () can be unique solved. Therefore,
where
By the Cramer's Role, we can solve and . Substituting () into yields that
where
Denoting Green function , then can be represented
Remark 6.1. Through above discussion, the case of eigenparameter appeared in the boundary conditions of both endpoints is different from the usual case [3], also different from the case of eigenparameter appeared in the boundary conditions of one endpoint[19], is not only determined by , but also related with .
7.
Conclusions
In this paper, a class of fourth order differential operators with eigenparameter-dependent boundary conditions and transmission conditions is considered. Using operator theoretic formulation, we transferred the considered problem to an operator in a modified Hilbert space. We investigated some properties of this operator, such as self-adjointness, sufficient and necessary conditions of the eigenvalues, asymptotic formulas for the fundamental solutions and the characteristic functions, the completeness of eigenfunctions in and the Green function.
Acknowledgments
The work of the author is supported by Natural Science Foundation of Shandong Province (No. ZR2020QA009, ZR2019MA034), China Postdoctoral Science Foundation (Nos. 2019M662313, 2020M682139) and the Youth Creative Team Sci-Tech Program of Shandong Universities (No.2019KJI007).
Conflict of interest
All authors declare no conflicts of interest in this paper.









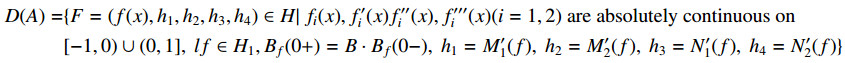
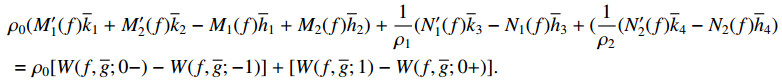
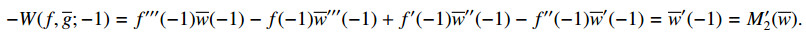
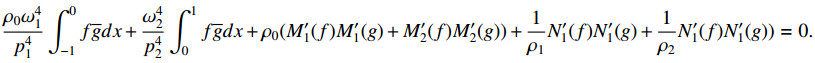
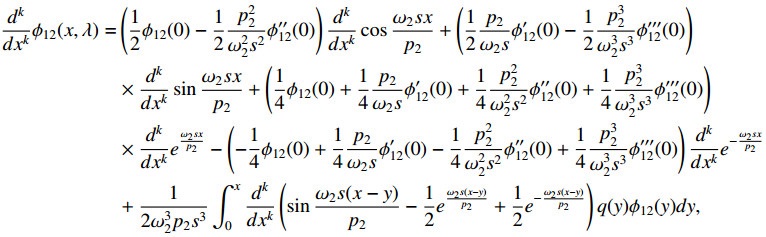
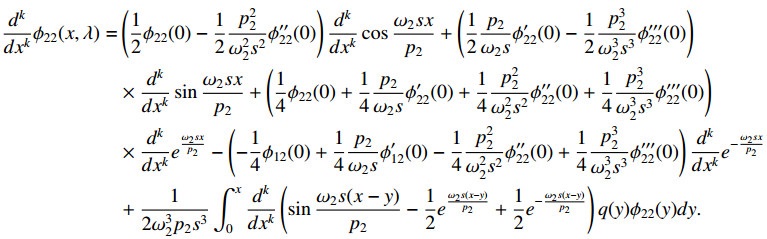
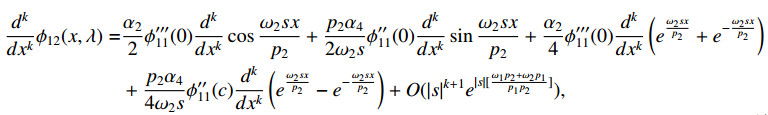
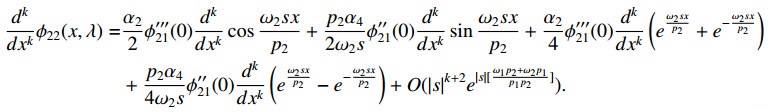
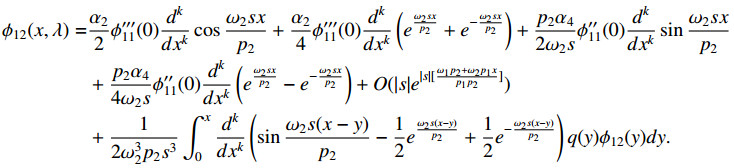
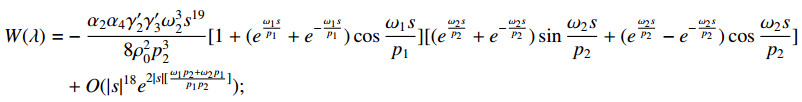
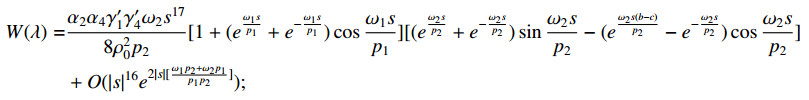
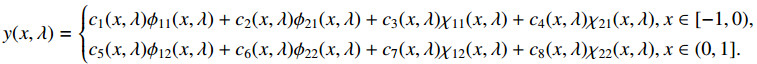
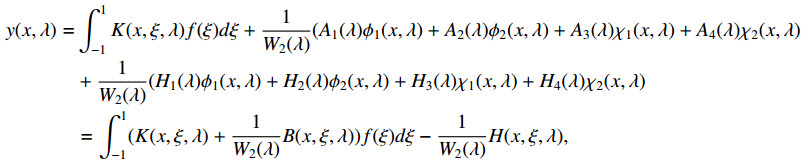





 DownLoad:
DownLoad: