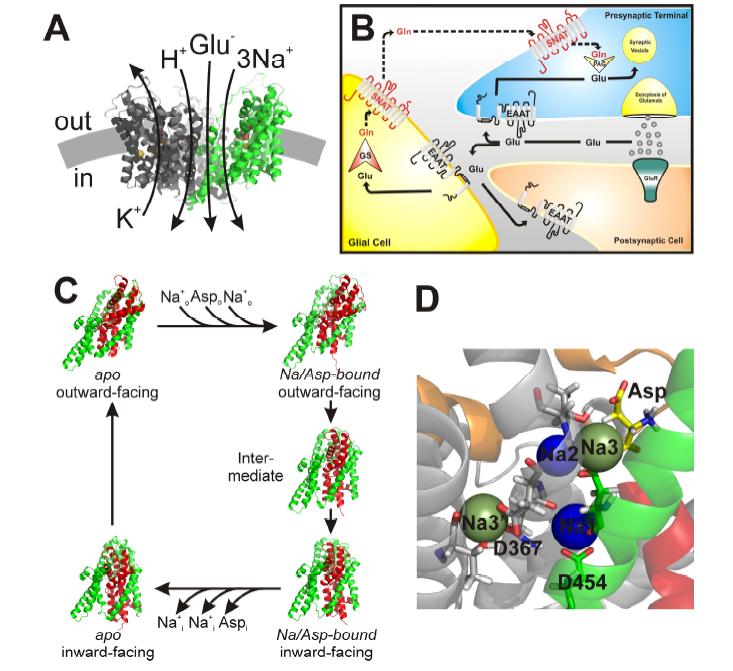
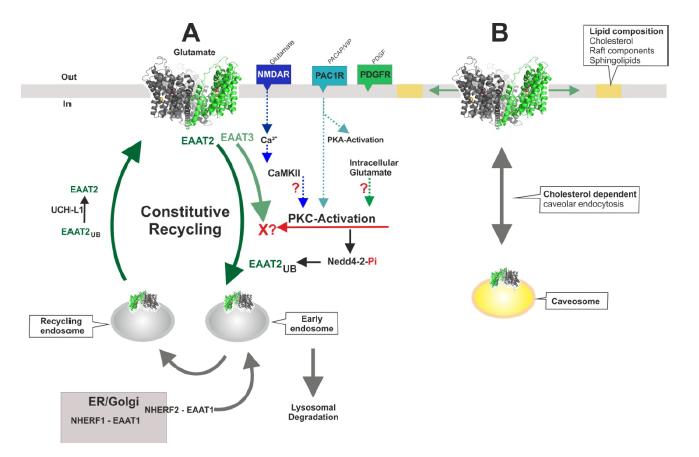
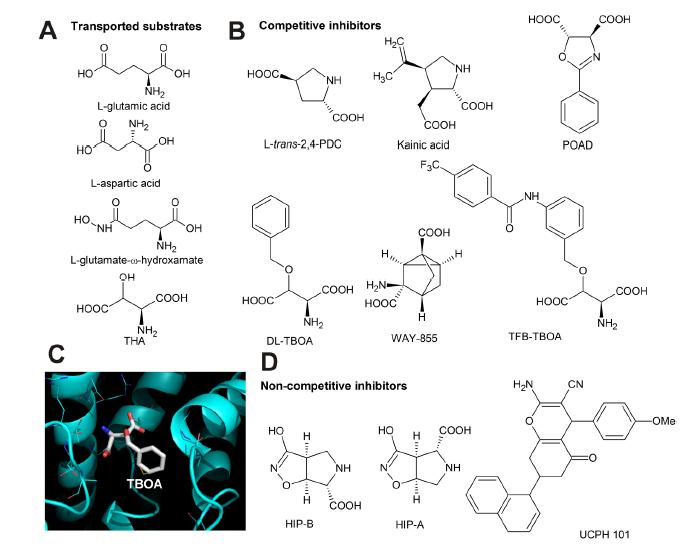
Glutamate transporters control the glutamate homeostasis in the central nervous system, and, thus, are not only crucial for physiological excitatory synaptic signaling, but also for the prevention of a large number of neurodegenerative diseases that are associated with excessive and prolonged presence of the neurotransmitter glutamate in the extracellular space. Until now, five subtypes of high-affinity glutamate transporters (excitatory amino acid transporters, EAATs 1–5) have been identified. These 5 high-affinity glutamate transporter subtypes belong to the solute carrier 1 (SLC1) family of transmembrane proteins: EAAT1/GLAST (SLC1A3), EAAT2/GLT1 (SLC1A2), EAAT3/EAAC1 (SLC1A1), EAAT4 (SLC1A6) and EAAT5 (SLC1A7). EAATs are secondary-active transporters, taking up glutamate into the cell against a substantial concentration gradient. The driving force for concentrative uptake is provided by the co-transport of Na+ ions and the counter-transport of one K+ in a step independent of the glutamate translocation step. Due to the electrogenicity of transport, the transmembrane potential can also act as driving force. Glutamate transporters are also able to run in reverse, resulting in glutamate release from cells. Due to these important physiological functions, glutamate transporter expression and, therefore, the transport rate, are tightly regulated. The EAAT protein family are structurally expected to be highly similar, however, these transporters show a functional diversity that ranges from high capacity glutamate uptake systems (EAATs 1–3) to receptor-like glutamate activated anion channels (EAATs 4–5). Here, we provide an update on most recent progress made on EAAT’s molecular transport mechanism, structure-function relationships, pharmacology, and will add recent insights into mechanism of rapid membrane trafficking of glutamate transporters.
1.
Introduction
In the last decades, combinatorial optimization problems have attract the interest of researchers due to the increase of dynamic environments applied on these problems, and researchers have developed mechanisms and methods to help optimization algorithms to adapt to changes that exist during the execution of these algorithms.
These problems can be represented by many production and services problems, including the reduction of the product's cost, improvement of logistic and company's profit. Furthermore, transport cost minimization is one of the cost reduction methods in which the mercancy is transported from an origin place to the one or several destinations with minimum cost [1].
Even defining Dynamic Combinatorial Optimization Problems (DCOP's or Dynamic COP's) is a challenging task due to applications in real problems such as transportation of products where there are a lot of not considered variables which cannot be identified until implementation on real cases. In general, researchers usually define optimization problems that change over time as Dynamic Problems, Time-Dependent Problems, or Dynamic Optimization Problems [2]. In existing metaheuristics studies, dynamic problems are defined as a sequence of static problems linked up by some dynamic rules or as a problem that have time dependent parameters in its mathematical model.
Usually, for static Combinatorial Optimization Problems (COP's), the goal of metaheuristics is to find the global optimum as fast and precise as possible, considering performance measures such as the convergence speed and the rate to get the optimum over multiple runs.
However, the goal of algorithms to solve DCOP's turns from to find the global optimum as fast as possible [3], to track the optimum as close as possible to real time on dynamic changes; in several cases, the algorithm needs to detect these changes, and then, it needs to track the local or global optimum. In addition, on environments where there exists a correlation between changes, the optimization algorithm needs to learn from its previous experience as a feedback to improve the search in the new solution space. Otherwise, the optimization process after each change will be explained like the process to solve different problems starting from the old population.
Heuristics and metaheuristics are methods that have been used to solve several problems in logistics as cost reduction in supply chain distribution [4,5] and facility location problems [6], even in manufacturing like optimization of manufacturing systems [7,8] and manufacturing models [9].
This research focuses on theoretical dynamic combinatorial problems to demonstrate the ability of a proposed mechanism to adapt in dynamic environments which could describe the behavior of a real problem. In this case, the mechanism was implemented in genetic algorithms to solve a travelling salesman problem which can be generalized in several problems, such as vehicle routing problem which is used in several areas of logistics and manufacturing. These mechanism is tested in other theoretical problems like One Max and 3-SAT problem to demonstrate the capability to solve binary problems, which are considered as simple problems but genetic algorithms search have a little complication to solve them due to the behavior and evolutive process of mutation and crossover operators.
2.
Dynamic optimization problems
Many dynamic optimization problems have been used in literature [10], many of them have features and can be classified into different groups based on some criteria:
● Time-Linkage: Whether the future behavior of the problem depends on the current solution found by an algorithm or not.
● Predictability: Whether the generated changes are predictable or not.
● Visibility: Whether the changes are visible to the optimization algorithm and whether the changes can be detected by using just a few detectors.
● Constrained problem: Whether the problem is constrained or not.
● Number of objectives: Whether the problem has single objective or multiple objectives.
● Types of changes: Detailed explanation of how changes occur in the search space.
● Cyclicity: Whether the changes are cyclic/recurrent in the search space or not.
● Periodicity: Whether the changes area periodical or not.
● Factors that change: Changes may involve parameters of objective functions, variables domain, variables number, constraints, among others.
2.1. Dynamic combinatorial optimization problems
The problems defined in this research are Travelling Salesman Problem (TSP) and One-Max problem, which have been considered in their static and dynamic form to extend the analysis of several assessments between a set of configurations for genetic algorithm and a self-adaptive mechanism proposed implemented in genetic algorithm to improve the search of solutions in dynamic environments. The algorithm will be explained in next section.
2.1.1. 3-SAT
This problem consists of a logical propositional formula in n variables and the requirement to find a value (true or false) for each variable that makes the formula true. This problem has N = 2n assignments. For k-SAT, the formula consists of a conjunction of clauses and each clause is a disjunction of k variables, any of which may be negated. For k≥3 these problems are NP-complete. An example of such a clause for k = 3, with the third variable negated, is V1 OR V2 OR (NOT V3), which is false for exactly one assignment for these variables: V1 = False, V2 = False, V3 = True.
3-SAT is one of Karp's 21 NP-complete problems [11], using Cook-Levin theorem to show that there is a polynomial time many-one reduction from the boolean satisfiability problem to each of 21 combinatorial and graph theoretical computational problems, thereby showing that they are all NP-complete. The instances that were used to test this problem were obtained from DIMACS-SATLIB Benchmark Problems.
2.1.2. Dynamic 3 SAT
To generate the dynamism in the 3-SAT problem, a strategy of insertion and elimination of conjunctions is used. At the beginning of the execution of the algorithm, only one strategy is selected to use it for the whole execution, the strategy can be generate a random conjunction with random variables or delete a random conjunction in the set of existing conjunctions. Since the original instance is the one of 3SATLib, when new conjunctions are inserted, it is not known in what will be the reaction of the new solutions. In the case of the elimination is an easier in this way because it does not increase the complexity of the problem, on the contrary, it reduces it.
2.1.3. One max problem
The One-Max Problem (or Bit Counting) is a simple problem consisting in maximizing the number of ones of a bit-string. Formally, this problem can be described as finding a string $\vec x = {x_1}, {x_2}, \ldots, {x_n} $ with ${x_i} \in 1 $, that maximizes the following equation:
Many authors, studying this problem, define this problem as a simple unimodal function and for a simple hill-climber using a traditional bit-flipping neighborhood search operator. However, a GA does not search over this simple 'Hamming' landscape. It is easy to analyze the landscape induced by a traditional NS operator, but the position is a little more complicated for the operators normally used by a GA, this is the reason of why this problem is important.
This is the simplest problem that can be selected, to convert this problem of a static environment to a dynamic environment is needed to change the search, it means, if the objective function is to find most of 1's in the solution, the change will be to find the most of 0s in the solution. This causes that the algorithms start to converge in determined generations, and when the change appears, all the solutions that have a good fitness, they are changing by the worst solution because they have the worst fitness in that moment.
2.1.4. Travelling salesman problem
TSP can be formulated as an integer linear program. Label the cities with the numbers $1, \ldots, n $ and define ${X_{i, j}} $, 1 if the path goes from city $i $ to city $ j$, and 0 otherwise. For $ {\rm{i}} = 1, \ldots, n$ let ${u_i} $ a dummy variable, and ${c_{i, j}} $ the distance from city $i $ to city $ j$. Then TSP can be written as:
2.1.5. Dynamic travelling salesman problem (DTSP)
DTSP have several real applications, especially in the optimization of dynamic networks, like planning and designing networks, load-balance routing, traffic management, among others.
An example of a DTSP is defined in [12] as a TSP with a dynamic cost matrix as:
where: $ {d_{i, j}}\left(t \right)$ is the distance cost from city $i $ to city $ j$, and $ n$ is the number of cities. DTSP can be defined as $f\left({x, t} \right) $, and the objective of DTSP is to find a minimum-cost route with all cities at time $t $. It can be described as follow:
where: $ x_{i} \in 1, 2, \ldots, n$ denotes the $ i$ -th city $i $ in the solution such that $x_{n}+1 = x 1 $ and, if $ i$ is different of $ j$, and $ {x_i}$ different of ${x_j} $.
This problem have been used in manufacturing problems such as distribution and routing problems [13,14,15] and in some cases to optimize facilities [16] and machines location [17].
3.
Solution algorithms
3.1. Genetic algorithm
Genetic Algorithms (GA's) have been developed in the 1970s by J. Holland to understand the adaptive processes of natural systems [18]. Then, they have been applied to optimization and machine learning in the 1980s [19,20].
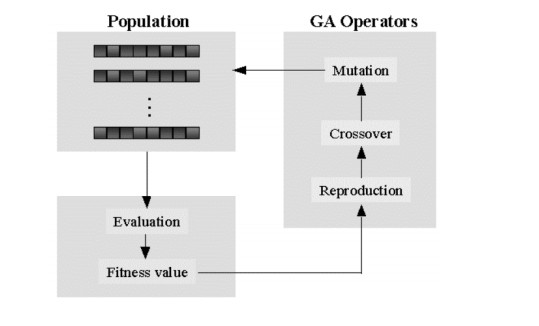
Genetic algorithms are defined in four steps: the first one is focused in the creation of a random population of candidate solutions according with the objective function. The second step is focused on each individual is evaluated in objective function. The third one, parents will be selected of the population, then is applied the crossover operator to these parents to build new solutions called children, then, the mutation operator is applied to these children. In the last step, children population will be the population for the new generation of parents, and this process will be repeated until a stop criterion defined [19]. This process is in Figure 1.
3.2. Adaptive and self-adaptive methods
It is well known that the values of parameter settings for metaheuristics has a great impact on their performance and this has attracted considerable interest in various mechanisms that in some way attempt to automatically adjust the algorithms parameters for a given problem. Adaptive and self-adaptive methods are developed to solve problems that have dynamic features.
In [20], there is a classification according to levels of adaptation or the mechanics on these methods. In mechanics classification exist: static, deterministic, adaptive and self-adaptive. In static methods the users need to define the parameters values manually; in deterministic, a heuristic function is defined to select the values; in adaptive, a heuristic function takes advantage of some feedback while the algorithm is running; and in self-adaptive, the parameters are encoded as part of individuals allowing the algorithm to operate directly on the parameters.
In self-adapt levels exists four classes: environment, population, individual and component. On environment level, the changes will be on fitness function; on population level, the changes will be on individuals set; on individual level, changes are directly related with each individual; and in component level, changes are made on each component of each individual, for example genes in genetic algorithm.
3.3. Self-adaptation methods on genetic algorithms
Adaptation and self-adaptation methods have been explored on genetic algorithm components, but these mechanisms do not have relevant improvements on all of them. The most considerable improvement is in mutation and crossover operations, where new genetic operators are generated to preserve the population distribution and a degree of diversity in future off-springs. Ingo Rechenberg proposed the first deterministic adaptation rule for mutation parameter, called the "1/5 rule", that indicates in each generation must exist 1/5 of total genes mutated. A proposal of a crossover operator is named Simulated Binary Reproduction (SBX), it is presented by Deb and Beyer in [22] where SBX creates children solutions in proportion to the difference in parent solution, their purpose is to obtain results as evolutionary strategies but as genetic algorithms. Another research [22] uses a genetic operator known as Multiple Crosses Per Couple (MCPC) in which the quantity of crossovers allowed per individual is encoded in the chromosome. Similar results are obtained via the design of self-adaptive crossover operator, specifying rules such as preservation of the statistical moments in distribution of the population and the diversity degree in future on-springs in [23], in this case, Uniformly Unimodal Distribution Crossover (UNDX) is defined.
Others researches [24] have developed the idea of Immigrants Schemes in genetic algorithms to solve dynamic routing problems, these schemes are based in random immigrants approach, which is a natural and simple way to maintain the diversity level of population through replacing some individuals of the current population with random individuals, called random immigrants, every generation. Usually there are two strategies to select individuals in the population that should be replaced: replacing random or the worst individuals. Authors [24] have used Memory Schemes at the same time, in this case, memory store useful information from the current environment, either implicitly through redundant representations or explicitly by storing best solutions of current population in an extra memory. The stored information can be reused later in new environments. Finally there are algorithms using hybrid immigrants and memory schemes.
4.
Mechanism description
The proposed mechanism is based on the idea of a genotype-phenotype mapping function which generates random values for each parameter of a Weibull probability distribution and finally through this distribution is obtained the value of each parameter of genetic algorithm. This mechanism belongs to self-adaptive methods in the individual level described in previous section. Before to explain how the mechanism works, genotype-phenotype mapping idea needs to be explained and how Weibull probability distribution works.
4.1. Genotype-phenotype mapping
The genotype and phenotype terms were created by Wilhelm Johannsen in 1911. Genotype is the complete hereditary information of an organism, even if it is not expressed. The Phenotype is a feature observed in the organism, such as morphology, development or behavior. This distinction is fundamental in the study of trait heredity and evolution. The strategy or method to map a set of genotypes to a set of phenotypes is call genotype-phenotype mapping. Genotype of an organism is an important factor in the development of its phenotype, but it is not the only one. Even two organisms with the same genotypes normally differ in their phenotypes [21].
The first studies about genotype-phenotype mapping in computation were elaborated on genetic programming in Banzhaf and Keller's work [23], they focused on Motoo Kimura's bio molecular research in 1968, where changes in molecules genotypes are phenotypically neutral are postulated, it means, several genotypes codified the same phenotype. These research is called Neutral Theory of Molecular Evolution of Motoo Kimura. Banzhaf and Keller proposed a genotype-phenotype mapping for genetic programming where they modified the non-viable genotypes to correct them with others nearby. An example in genetic algorithms is show in [25], where authors described a strategy to guide the search according with mutation. The evolutive advantage is given by some synonyms mutate towards more significant phenotypes than others.
Synonyms are explored in a more detailed way in Rothlauf y Goldberg's work [26] where they described that not all kind of representations are useful in the context of evolutive algorithms. A representation is defined as synonomically redundant if the genotypes associated with the same phenotype are similar, this concept is formally defined in terms of the sum of all distances between pairs of genotypes obtained from the set of genotypes that encodes a phenotype. If each phenotype is represented by the same number of genotypes, it means that the representation is uniformly redundant, one genotype is neighbor to another if the distance between them is the least possible, if neighboring genotypes throw neighboring phenotypes, the representation have a high locality.
In Ohnishi's work [27] is explained a mutation-based evolutionary algorithm that evolves genotypic genes for regulating developmental timing of phenotypic values. The genotype sequentially generates a given number of entire phenotypes and then finishes its life at each generation. Each genotypic gene represents a cycle time of changing probability to determine its corresponding phenotypic value in a life span of the genotype.
In Fagan's work [28] are explained some approaches that use genotype-phenotype mapping in genetic programming, and they focused on performance, it means, they examined different ways of implementing this mapping from chromosome to solution and investigate the possibility of the existence of mappings that are more suited to certain types of problems, or if a general mapping can be found which exhibits acceptable performance across all problem domains.
4.2. Weibull distribution function
Probability distribution functions were used to define the mapping function in which a genotype represents a phenotype, these functions were used indirectly to generate values for each parameter in the algorithms, and this is the reason to explain each section of the proposed mechanism.
A probability distribution is a mathematical function that represent the probabilities of occurrence of different possible outcomes in an experiment, it is a description of a random phenomenon according with their respective probabilities of events.
There are a lot of probability distribution, but this research focuses on evaluate 3 different distributions to select the best one, normal, exponential and Weibull distributions were tested. The Weibull distribution function got the best results according to proposes of this research, due to it is too simple to manipulate the values of its parameters to generate many forms, and this behavior helps the adaptation of each parameter on a genetic algorithm. That's the reason Weibull distribution is the only probability distribution mentioned on this research.
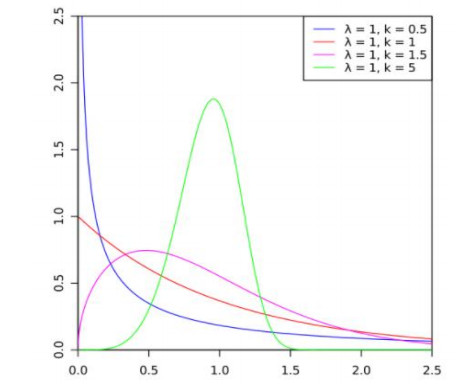
Weibull distributions can be seen as a generalization of the exponential distribution as such as the gamma distribution. This distribution is commonly used for modeling reliability or survival data. It has two parameters: $ k > 0$ is the shape parameter and $\lambda > 0 $ is the scale parameter, which allow it to handle increasing, decreasing or constant failure-rates. Weibull distribution effectively describes the time we have to wait for one event to occur, if that event becomes more or less likely with time. Here the $ k$ parameter describes how quickly the probability ramps up.
It is defined as:
Its complementary cumulative distribution function is a stretched exponential function. If the quantity x is a time-to-failure, the Weibull distribution gives a distribution where the failure rate is proportional to a time power. The pdf for the Weibull distribution drops off much more quickly (for $ k > 1$) or slowly (for $ k < 1$) than a gamma distribution. In the case where $ k = 1$, they both reduce to the exponential distribution, this particularity makes this distribution special against others. The shape parameter $ k$ can be interpreted directly as follows:
● A value of $ k < 1 $ indicates that the failure rate decreases over time. If there is significant mortality or defective items failing early, and the failure rate decrease over time as the defective items are eliminated of population.
● A value of $ k = 1$ indicates that the failure rate is constant over time. This suggest that random external events are causing mortality or failure.
● A value of $ k > 1$ indicates that the failure rate increases over time. If there is an aging behavior or parts that start to fail as time goes on.
Figure 2 shows how this distribution changes according with different values for parameters.
4.3. Proposed mechanism
The algorithm is based on the idea of a genotype-phenotype mapping function which generates random values for each parameter in genetic algorithm based on a Weibull distribution, the idea is to incorporate parameters of the algorithm to evolve in each generation with the population, but, each individual has their own value for each parameter, it means, each individual has their own mutation probability and selection probability.
4.3.1. Generating individuals
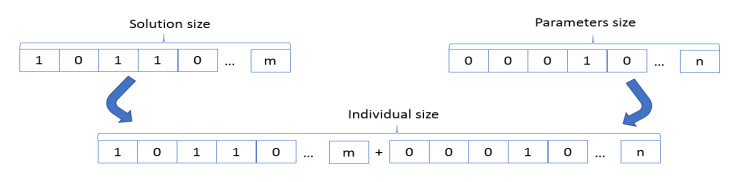
First, to generate each individual for genetic algorithms is needed to consider two aspects, the first one is the individual size, it represents the original size for a solution that solves the problem; the second aspect is focused on considered size for the Weibull distribution parameters, each individual on population contains the own parameters $k $ and $\lambda $ to generate a Weibull distribution (see Figure 3).
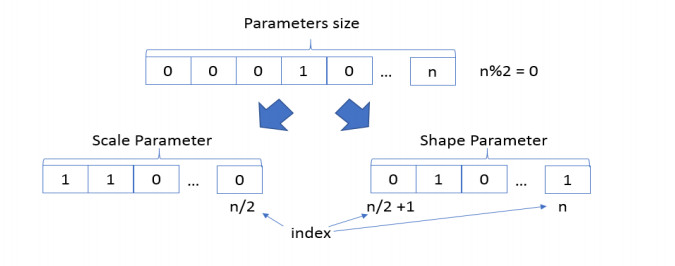
Segment on each individual that consider the Weibull distribution parameters needs satisfy two features: a) Size needs to be even. b) Size is represented in binary code. The feature (a) is defined due to segment is divided in two parts, the first one represents the value for $ \lambda $ and the second part represents the value for $ k$, and both parameters need the same quantity of binary elements to map their values in decimal integers. The feature (b) is defined because is easier to work with binary values in most of the algorithms, it is recommended that the parameters representation must be binary, to satisfy this representation is needed a mapping function that transforms binary values into integer decimal values for each parameter (see Figure 4).
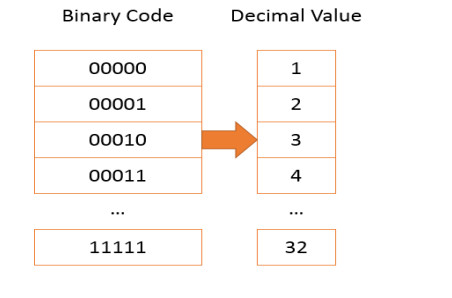
To define the size of the mapping function to transform the parameters, it is necessary to define the lower and upper limits that will be used for the Weibull parameters; the minimum recommended value for $ k$ and $ \lambda $ is 1, to avoid the form that this distribution has between the 0-1 values, because it tends to be a logarithmic distribution, and it does not give good results for mechanism purposes; the upper limit value is recommended to use values according to the number of binary bits to be used, if it is necessary to handle only 3 bits it is recommended to use a limit size of 8, if it needs to use 4 bits a limit of 16, for 5 bits a limit of 32, and so on, this is to avoid normalizing from decimal to binary values (see Figure 5).
4.3.2. Generating random values with Weibull distribution
With parameters $ k$ and $ \lambda $ is possible to generate a Weibull distribution, it just needed to substitute these values on Equation 4, then the distribution generate the Cumulative Distribution Function (CDF). The CDF is used to generate random numbers in a range defined by the Weibull distribution through the Inverse Transformation method.
Inverse Transformation is a method that used the cumulative distribution function F(x) of the Weibull distribution, being that F(x) is defined in the interval (0, 1), it is possible to generate a uniform random number $ R$ and try to determine the value of the random variable for which the cumulative distribution is equal to $ R$, it means, simulated value of the random variable that follows a probability distribution f(x) is determined by solving the following equation:
And for Weibull distribution the inverse function is:
where ${\rm{u}} $ is a random value $\mathrm{u} \in \mathrm{U}(0, 1) $.
4.3.3. Generating random parameters for algorithms
Finally, it is necessary to generate a mapping function that transforms the obtained random value to a value that represents a parameter of the algorithms, in GA, the parameters that the algorithm used are commonly probabilities and this is the reason that the parameters need to be mapped between 0 and 1 values.
The mapping function is defined to evaluate and to obtain the parameter values for genetic algorithm. The value obtained from the CDF is divided by the maximum value that can be obtained in the Weibull distribution, this is to normalize it in the range of 0 and 1, and it is the new value for each parameter.
4.3.4. Mechanism in genetic algorithm
Genetic algorithms have two main operators, crossover and mutation, and their values can be between 0 and 1. The idea of how the mechanism works is based on the mutation and crossover operators for binary individuals, it means, the segment that represents the parameters on each individual will evolve with this genetic operators on each generation, but the operators will focus on evolve this segment such as if algorithm were solving a binary problem; if the original problem is defined in a non-binary space, such as combinatorial problems, the segment that represents the individuals will be solved with genetic operators focused on this kind of problem, nevertheless, the segment which represent the parameters will be solved as a binary problem. The pseudo-code that represents this idea is explained in Figure A1 Appendix A.
5.
Results
The implementations were tested and benchmarked in 3 experiments. In the first experiment the One-Max problem was tested, this problem was configured on two instances with 50 and 500 bits length respectively. The second experiment was tested on TSP problem with TSPLib where 2 instances were obtained called "a280" and "ulysses22", where problems have 280 and 22 cities respectively, the matrix distance is obtained with Euclidean distance between cities. In third experiment 3-SAT problem was evaluated, this problem was configured on two instances with 20 variables and 91 clauses, these instances where selected from SATLib library, the files are in DIMACS CNF format, a standard format of instances of SAT developed in the nineties to express Boolean satisfaction problems in a normal conjunctive way (that is, where the problem is expressed as a conjunction of clauses and a clause is a disjunction of literals). On each dynamic instance, the changes were realized every 50 generations and every 300 generations. For both experiments, 100 runs were generated for each instance, and the average of the results were used to compare the algorithms. Due to the particular features of 3-SAT problems, 4 rules to identify dynamism in problems were: problem was updated every 50 generations and every 300 generations, and the process was to delete clauses and to add clauses. All experiments were tested in a computer with Intel i7-4800MQ processor with 2.7 GHz and 16GB RAM. Implementations were coded using Java version 8, jdk 1:8:092 and jre 1:8:0144.
The algorithms used to compare the mechanism proposed was selected by their results in an analysis realized previously through a Design of Experiments (DOE) to prove which configuration(s) of genetic algorithms are the best to solve these problems. The parameters used to generate these configurations were population, mutation probability and crossover probability. The values considered for each parameter on this DOE were:
Mutation Probability = .1, .5 y.9
Crossover Probability = .1, .5 y.9
Population = 50, 150, 300
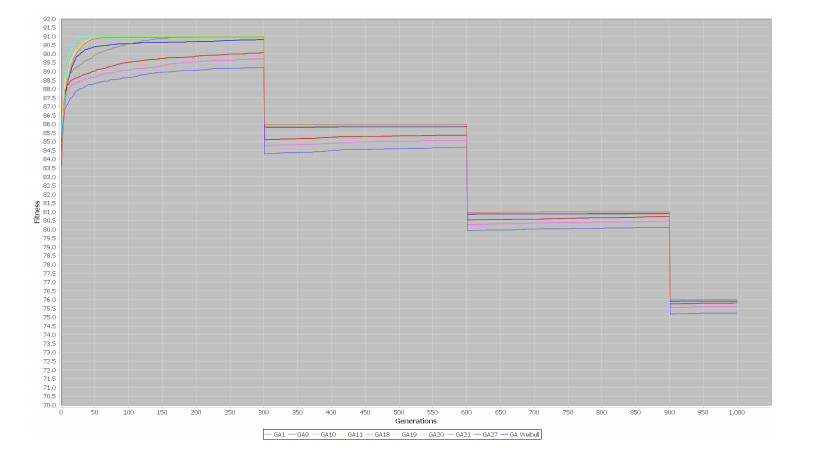
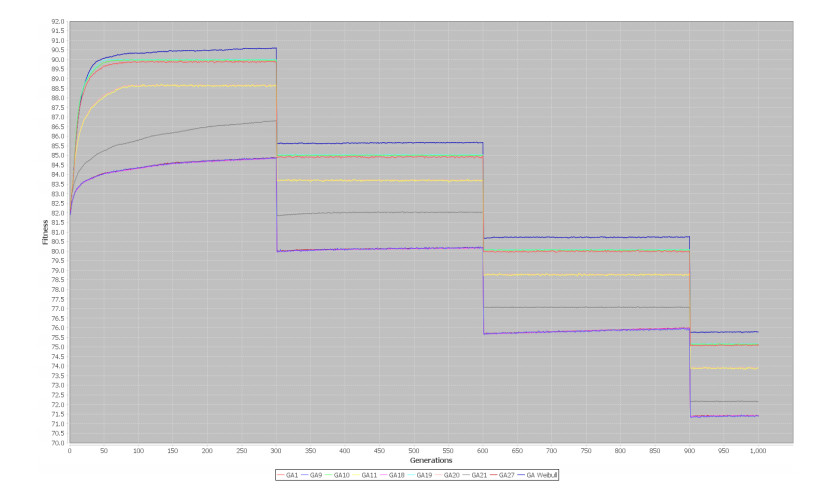
With these values were obtained 27 different configurations for the GA. The results obtained in the first experiment for these 27 algorithms are shown in the Figures B1-B2. These results demonstrate that each configuration has a specific behavior when it tries to get the result for genetic algorithm, this is the reason that for each combination values for each parameter were created different clusters to identify the main feature that solve in a better way that problem, in case of the first experiment in its dynamic environment, results are shown in Figures B3-B4. These behaviors were similar on each problem, in Figures B5-B6 are results obtained by experiment 2 in static environment and in Figures B7-B8 in dynamic state. For the last experiment, in Figure B9-B10 are shown only results obtained for static environment to these configurations in genetic algorithm, due to the particular features described previously on this section.
The algorithms were selected according to the best results obtained and the population with a balance between exploration and exploitation strategies, all results obtained for each configuration on each problem defined in experiments were classified on different clusters, in Figures B11-B12 are shown the clusters for the analysis on One-Max problem, in Figures B13-B14 for TSP problem and in Figures B15-B16 for 3-SAT problem, on these graphs, a clustering strategy was used to identify the features of the algorithms with the best results for each problem. There exist three different clusters, the first one represents the better configurations that get best average global fitness and the population is to near of the optimal, they are represented by the biggest circles in the graphs, the features that describe these behaviors for each cluster is represented on Table 1.
According with clusters and features identified for each configurations to solve these problems, for each problem, the best configurations of parameters were selected, for each problem 3 different configurations such as is shown in Table 2.
For each problem several configurations for genetic algorithm have good results to solve it, to demonstrate these results, on Figure B17, Figure B18 and Figure B19 are shown the three configurations with best results for each problem.
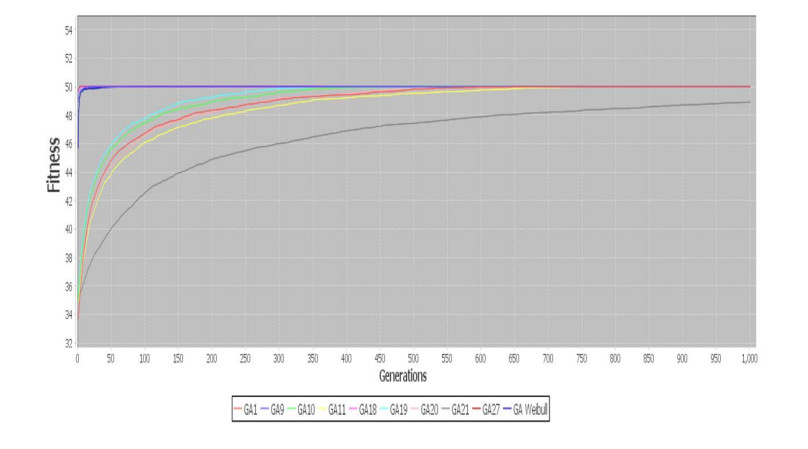
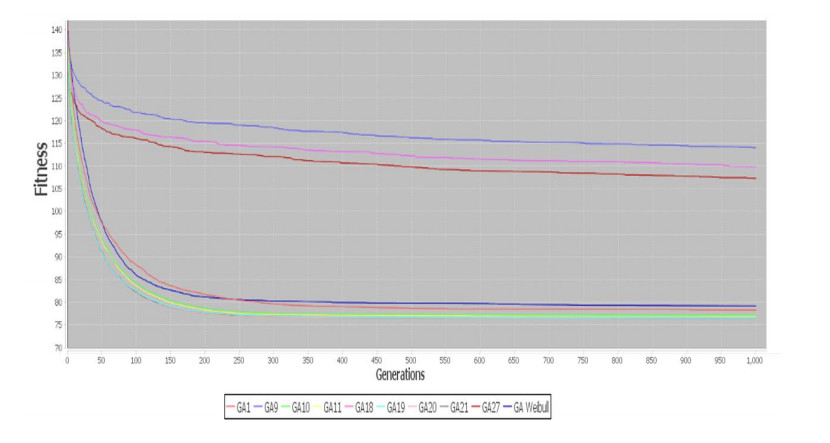
The parameters to test the mechanism were mutation probability and crossover probability. The mechanism proposed was evaluated in static problems and in dynamic problems, results are shown in Figure 6 and Figure 7, to ensure that it will have good results in static problems and not only in dynamic problems, the main objective for this research is to evaluate if mechanism help genetic algorithms to change the exploration and exploitation strategies when combinatorial problems have dynamic changes over time.
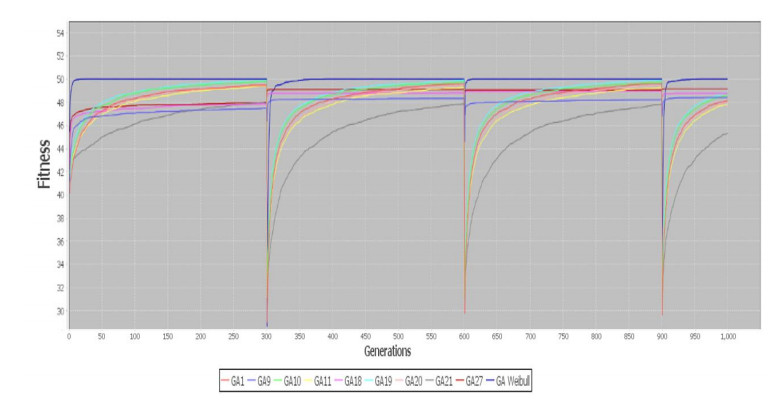
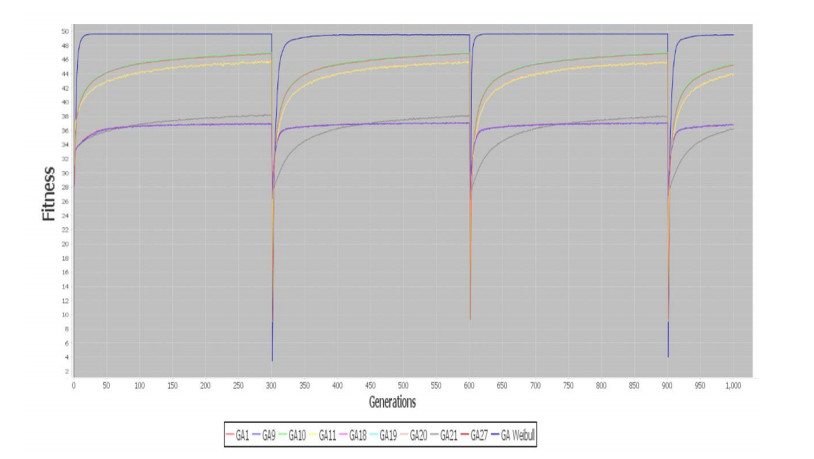
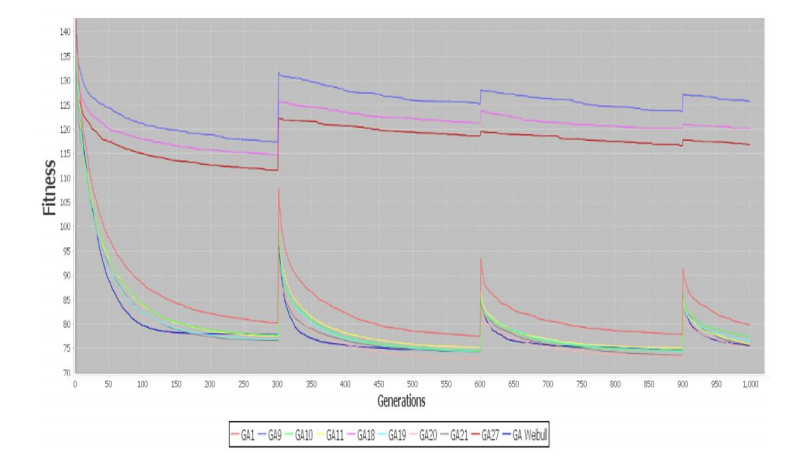
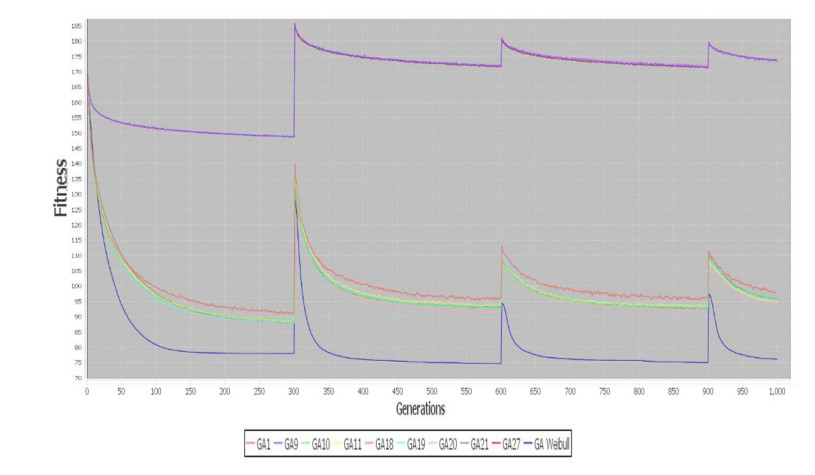
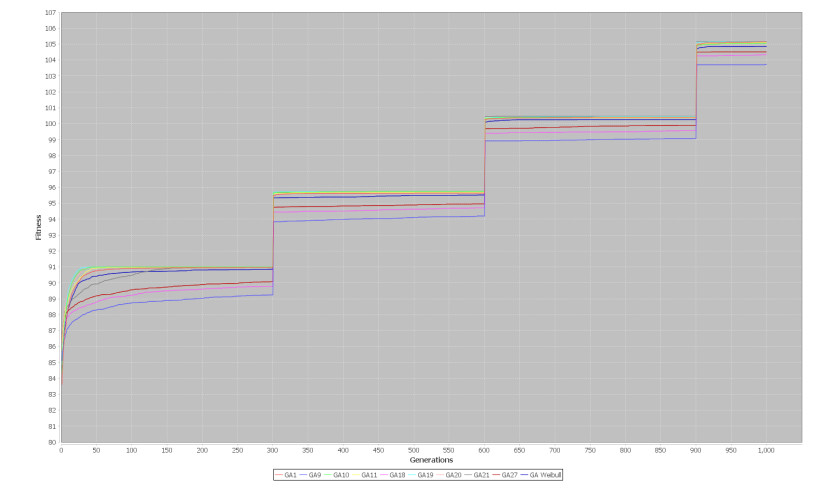
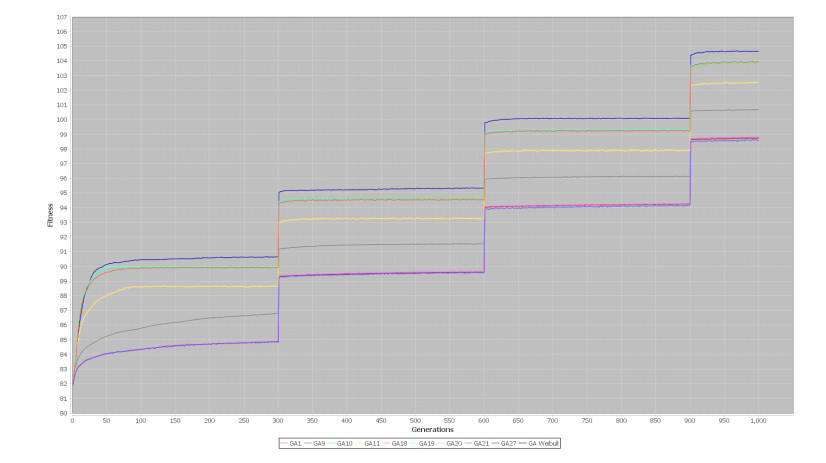
In Figures 8-11 are represented the results about dynamic problems, in both cases the mechanism improves the genetic algorithm and it helps to track the optimal solution when a change occurs, in all graphics the mechanism is represented by the blue line with the best results. On each algorithm, results obtained for each configuration are shown in Table 3 for One Max, Table 4 Dynamic One Max, Table 5 TSP and Table 6 Dynamic TSP.
In case of results for 3-SAT problem, 4 rules were defined to identify dynamism in this kind of problems. In Figure 12 and Figure 13 are represented the best and average results for dynamic environment for 3-SAT problem adding 5 clauses each 300 generations. In Figure 14 and Figure 15 are represented the best and average results for dynamic 3-SAT problem deleting 2 clauses every 300 generations. On this experiment is represented with figures just the 3-SAT problem with changes every 300 generations, in the other case, changes every 50 generations, has the same behavior but the graphs do not show the changes as clearly as they are shown in these figures.
On each algorithm, results obtained for each configuration are shown in Table 3 for static 3-SAT, Table 4 Dynamic 3-SAT problem adding 5 clauses every 50 generations, Table 4 TSP and Table 5 Dynamic TSP. In the next tables, the information is limited to shown the three best configurations for genetic algorithm to solve this problem due to the large amount of information on each table.
6.
Discussion
The main conclusion is, at least for the proposed experiments, if genetic algorithm uses the mechanism proposed, it improves a lot the strategy to search optimal solutions in dynamic problems. When the problem changes overtime, the mechanism does not have any problem to adapt when changes occur, it has the advantage to find the optimum to fast and it helps the population to converge to this value(s). When a change occur, the algorithm is helped by the mechanism to get out of local optimum solution and to find another optimal solution, it indicates that the self-adaptation is responsible to change the diversification by an intensification strategy when the algorithm needs to find solutions in new areas, moreover, it changes diversification by intensification when there not exist changes in the solution space and the algorithm needs to find solutions in the shortest possible time, the mechanism can manage the changes between these strategies because it increased or decreased the mutation and crossover probabilities according with needs of the algorithm, due to each individual in the population has the own probabilities, each individual has different mutation and crossover probabilities and these values depend of a distribution probability function which evolves at the same time that the population evolves, it means, each individual will evolve independently depending on the individuals which it intersects and the mutations that receives on each generation, and in case of changes in the environment, the evolution of its parameters will be as drastic as possible depending on the fitness it have in the moment of changes. Furthermore, if the solution space has more than one optimal solutions, the mechanism improves the possibility to find them all.
Solutions demonstrates that mechanism improves the performance of genetic algorithms to solve these problems, and it indicates that it can be implemented in generalized problems as vehicle routing problems in some practical cases, just is needed to adjust objective function, variables and restrictions of real problem.
As future work, this mechanism will be implemented in other algorithms as Particle Swarm Optimization and Ant Colony Optimization, it will be used to solve more complex problems and to modify another parameters such as population in genetic algorithms. It will be compared with existing self-adaptive mechanism and it will be tested to solve vehicle routing problems in logistic real cases.
Acknowledgments
We would like to thank CONACyT for funding this research.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: