Gradient Lagrangian systems and semilinear PDE

Dedicated to Alberto Farina on the occasion of his 50th birthday.

1.   Introduction

We met Alberto, when we were all younger, in 1998 in Paris. Since then we have had the privilege of enjoying his friendship and sharing with him some math. It is a real pleasure to contribute to this volume to celebrate Alberto's fiftieth birthday.

At that time Alberto's research was focused on the study of Liouville type theorems and related symmetry properties for entire solutions of Ginzburg Landau systems or Allen Cahn type equations in $\mathbb{R}^{N}$(see ^[25,26]). These studies led him to the proof of the celebrated Gibbons conjecture in ^[27] (see also ^[28]), proving that

Theorem 1.1. ^[27] Let $N > 1$ and $u\in {{\cal C}}^{2}(\mathbb{R}^{2})$ be a bounded solution to $-\Delta u+u(u^{2}-1) = 0$ such that $\lim_{x_{1}\to \pm\infty}u(x) = \pm1$ uniformly with respect to $(x_{2}, \ldots, x_{N})\in \mathbb{R}^{N-1}$. Then $u(x) = q(x_{1})$ on $\mathbb{R}^{N}$ where $q\in {{\cal C}}^{2}(\mathbb{R})$ is a solution of the ordinary differential equation $-\ddot q+q(q^{2}-1) = 0$ on $\mathbb{R}$ and $\lim_{t\to\pm\infty}q(t) = \pm 1$.

In ^[27], Theorem 1.1 has been proved to hold for a wide class of double wells bistable potentials $F(u)$ modeled on that of Ginzburg Landau. The same results had already been obtained in ^[40] in the cases $N = 2, 3$ and then for each $N > 1$, independently of ^[27], in ^[16].

This kind of qualitative analysis of "rigidity" results for semilinear elliptic equations remained until now one of the main research themes developed by Alberto. Among others, we refer to the papers ^{[29,30,31,32,33,34,35,36,37,38]} where different aspects of this line of study have been deeply investigated for various models, including the Allen Cahn type equations (in relation with the study of the De Giorgi conjecture ^[24]), Nonlinear Schrödinger equations, quasilinear elliptic equations and Gross–Pitaevskii systems.

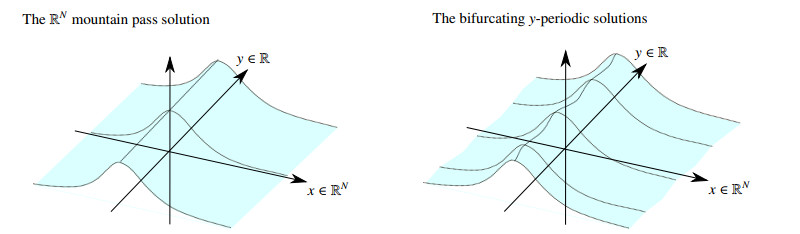
These symmetries are generally lost and multiple differently shaped solutions appear when one considers non autonomous or higher dimensional problems, see e.g., ^{[1,2,4,5,6,7,8,9,10,12,23,47,52,53,54,55]}. In Section 2 we describe some of these multiplicity results for Allen Cahn models. In particular we emphasize how the Lagrangian structure of the problem allows to obtain infinitely many solutions viewed as orbits of an infinite dimensional Newtonian system connecting disjoint well separated subsets of a fixed sublevel of the related potential. An application of the same method, as done in ^[11], is described for the Nonlinear Schroedinger equation in Section 3 and, related to this problem, Section 4 is devoted to characterize metric separation properties of sublevels sets of the "potential" functional $V(u) = \tfrac 12\|\nabla u\|_{H^{1}(\mathbb{R}^{N})}^{2}-\tfrac 1{p+1}\| u\|_{L^{p+1}(\mathbb{R}^{N})}^{p+1}$, for different values of the exponent $p+1\in (2, 2^{*}_{N})$ (see Propositions 4.1 and 4.2).

2.   Layered solutions for Allen Cahn models

Consider the Allen Cahn type equation

where the potential $F\in C^{2}(\mathbb{R}^{N}\times \mathbb{R})$ is $1$-periodic in the space variables $x_{i}$, $i = 1, \ldots, N$, and it is of double well type in the variable $u$, i.e.,

Look at the problem of finding solutions $u\in C^{2}(\mathbb{R}^{n})$ of (2.1) satisfying

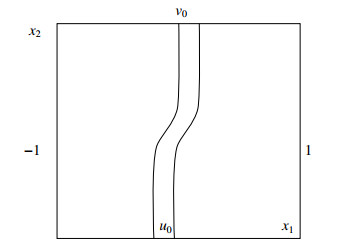
Rabinowitz and Stredulinsky in ^[52,53] proved that problem (2.1)–(2.3) generically admits a rich variety of geometrically different solutions connected to each other. They first showed by variational methods the existence of minimal solutions of (2.1)–(2.3) which are 1-periodic with respect to the variables $x_{2}, \ldots, x_{N}$. Moreover, the set of such minimal solutions, $\mathcal{M}_{0}$, is an ordered set in the sense that if $u_{0}, v_{0}\in{{\cal M}}_{0}$ then either $u_{0} > v_{0}$ or $u_{0} = v_{0}$ or $u_{0} < v_{0}$ on $\mathbb{R}^{N}$. Hence an alternative occurs, either

i) for any $y\in (-1, 1)$ there is $x_{0}\in \mathbb{R}^{N}$ and $u\in{{\cal M}}_{0}$ such that $u(x_{0}) = y$ (the graphs of the minimal solutions foliate $\mathbb{R}^{N}\times (-1, 1)$); or

ii) ${{\cal M}}_{0}$ has a gap pair: there exist $u_{0} < v_{0}\in{{\cal M}}_{0}$ such that no member of ${{\cal M}}_{0}$ lies between $u_{0}$ and $v_{0}$.

Note that (i) is always satisfied in the autonomous case, as for $F(u) = \tfrac 14(u^{2}-1)^{2}$ like in Theorem 1.1, since the problem is invariant by translation. On the other hand, as proved by Rabinowitz and Stredulinski, the case (ii) occurs generically for periodic potentials $F$ satisfying (2.2) (see ^[54]).

If case (ii) occurs other solutions appear. If $u_{0} < v_{0}\in{{\cal M}}_0$ is a gap pair, they proved the existence of another ordered family $\mathcal{M}_{1}$ of minimal solutions of (2.1)–(2.3), between $u_{0}$ and $v_{0}$, which are asymptotic as $x_{2}\to\pm\infty$ to the elements of the gap and are 1-periodic in the remaining variable $x_{3}, \ldots, x_{N}$ (see Figure 1).

If the ordered set $\mathcal{M}_{1}$ has itself a gap pair, $u_{1} < v_{1}$, the argument can be repeated to find ordered classes of minimal solutions connecting $u_{1}$ and $v_{1}$ and the reasoning can be iterated to obtain higher dimensional connections. When gaps are present in ${{\cal M}}_{0}$, variational gluing techniques were moreover employed to construct multitransition type solutions of (2.1)–(2.3), solutions which oscillate with respect to the variable $x_{2}$, in a prescribed fashion, between the elements of the gap, being periodic in the variables $x_{3}, \ldots, x_{N}$ (see the monograph ^[54] for an exposition of such kind of results in connection with the Moser-Bangert Theory ^[14,48]).

Unlike the rigid character of Allen Cahn's autonomous equation, as described in Theorem 1.1, these studies show how the solutions set of (2.1)–(2.3) may be complex when the potential explicitly depends on the spatial variables.

The contrast between these results and the Gibbons conjecture is even more explicit considering potentials $F$ depending (1-periodically) only on the space variable $x_{1}$. In this case any solution $q\in C^{2}(\mathbb{R})$ of the heteroclinic one dimensional problem

generates a solutions $u(x) = q(x_{1})$ of (2.1)–(2.3). The set ${{\cal M}}_{0}$ corresponds here to the set of minimal solutions of (2.4), i.e., the set

where

The minimal set ${{\cal K}}$ is ordered and if it has a gap pair $q_{0} < q_{1}$ the above results give the existence of $u\in C^{2}(\mathbb{R}^{N})$ solution to $-\Delta u+F_{u}(x_{1}, u) = 0$ on $\mathbb{R}^{N}$ satisfying (2.2) and being asymptotic, as $x_{2}\to\pm\infty$, to $q_{0}$ and $q_{1}$ (not depending on the others variable $x_{3}, \ldots, x_{N}$). Then, even if the nonlinearity depends only on the variable $x_{1}$, differently from the autonomous case, problem (2.1)–(2.3) has solutions which do not come from the one dimensional problem (2.4).

This result was originally obtained with L. Jeanjean in ^[4] (see also ^[5]), pointing out how Theorem 1.1 is a particular feature of the autonomous Allen-Cahn stationary equation. In ^[4] a factorized case was considered, $F(t, u) = a(t)W(u)$ with $a$ positive and periodic and $W$ a double well potential, but the arguments does not change for general potential $F(x_{1}, u)$ satisfying (2.2). It is worth mentioning that in ^[4], the ordered structure of the minimal set ${{\cal K}}$ was not used and the above gap condition, (ii), was formulated in terms of a separation property of the minimal set ${{\cal K}}$:

$(*)$ there exists ${{\cal K}}_{0}\subset{{\cal K}}$ such that, setting ${{\cal K}}_{j} = \{ q(\cdot-j)\, |\, q\in{{\cal K}}_{0}\}$ for $j\in{{\bf Z}}$, there result

$(i)$ ${{\cal K}}_{0}$ is compact with respect to the $W^{1, 2}(\mathbb{R}, \mathbb{R}^{N})$ metric,

$(ii)$ there exists $\rho_{0} > 0$ such that if $i\not = j$ then ${{\mathrm{dist}}}_{L^{2}(\mathbb{R})} ({{\cal K}}_{i}, {{\cal K}}_{j})\geq \rho_{0}$,

$(iii)$ ${{\cal K}} = \cup_{j\in{{\bf Z}}}{{\cal K}}_{j}$.

Thanks to the ordering property of ${{\cal K}}$ and its invariance with respect to integer translations, the existence of a gap pair in ${{\cal K}}$ is in fact equivalent to the property $(*)$. In ^[4] are given examples of singularly perturbed cases verifying $(*)$ and, moreover, it has been proved that $(*)$ does not hold if and only if ${{\cal K}}$ is a continuum with respect to the $W^{1, 2}(\mathbb{R})$ metric, homeomorphic to $\mathbb{R}$. It should be interesting to understand, in relation with the Gibbons conjecture, what happens when ($*$) is not satisfied (see ^[46] for a related study).

The work in ^[4] was motivated by the paper of S. Alama, L. Bronsard and C. Gui, ^[1], where they study a vectorial version of the Allen Cahn model. More precisely for potentials $F\in{{\cal C}}^{2}(\mathbb{R}^{2})$ satisfying

$(F_{1})$ $F((\pm1, 0)) = 0$, $F(\xi) > 0$ for every $\xi\in \mathbb{R}^{2}\setminus\{(\pm 1, 0)\}$, $D^{2}F((\pm 1, 0))$ are definite positive and there exists $R > 0$ such that $\nabla F(\xi)\xi\geq 0$ for $|\xi| > R$;

$(F_{2})$ $F(-\xi_{1}, \xi_{2}) = F(\xi_{1}, \xi_{2})$ for any $(\xi_{1}, \xi_{2})\in \mathbb{R}^{2}$,

they look for the existence of solutions $u\in C^{2}(\mathbb{R}^{2}, \mathbb{R}^{2})$ to the problem

Again, in their study, an important role is played by the structure of the set of one dimensional minimal solutions to (2.5) and (2.6), ${{\cal K}}_{s}$, the set of minima of the action $V(q) = \int_{ \mathbb{R}}\tfrac12|\dot q|^{2}+F(q)\, dx$ on the class of symmetric functions

In ^[1] it is proved that ${{\cal K}}_{s}\not = \emptyset$ and if

($**$) ${{\cal K}}_{s} = \{ q_{1}, \dots, q_{k}\}$ with $k\geq 2$ and $q_{i}\not = q_{j}$ when $i\not = j$,

then there exists a solution $u\in C^{2}(\mathbb{R}^{2}, \mathbb{R}^{2})$ of (2.5)–(2.6) which is asymptotic as $y\to\pm\infty$ to a pair of different elements in ${{\cal K}}_{s}$, showing the failing of Gibbons-like results for autonomous systems.

The symmetry assumption $(F2)$ is used in ^[1] to gain compactness in the problem working with the symmetric functions in $\Gamma_{s}$. That assumption was later dropped in ^[55], by M. Schatzman, showing how it is possible to overcome the lack of compactness assuming a nondegeneracy property of the one dimensional heteroclinic connections. Precisely, letting

in ^[55] it is assumed that

$(***)$ there exists $z_{-}\not = z_{+}\in{{\cal K}}$ such that

(i) ${{\cal K}}$ decomposes in the disjoint union of the sets of the translated of $z_{-}$ and $z_{+}$:

(ii) the operators $A_{\pm}:H^{2}(\mathbb{R}, \mathbb{R}^{2})\subset L^{2}(\mathbb{R}, \mathbb{R}^{2})\to L^{2}(\mathbb{R}, \mathbb{R}^{2})$, $A_{\pm}h = -\ddot h+D^{2}W(z_{\pm})h$, are such that $\mathrm{Ker}(A_{\pm}) = \mathrm{span}\{\dot z_{\pm}\}$.

The non degeneracy condition $(***)$-(ii) allows to gain compactness in the directions orthogonal to $\mathcal{C}(z_{\pm})$, and in ^[55] this is used to obtain the existence of a solution $u\in C^{2}(\mathbb{R}^{2}, \mathbb{R}^{2})$ of (2.5)–(2.6) such that $\lim_{y\to\pm\infty}u(x, y) = z_{\pm}(x-s_{\pm})$ for certain values $s_{\pm}\in \mathbb{R}$.

The results in ^[1,4,55] have been obtained by variational methods. Differently from ^[1], where a limit procedure throught domains in $\mathbb{R}^2$ bounded in the $y$ direction was employed, in ^[4] the two dimensional solutions in ${{\cal M}}_{1}$ were found as minima of a global functional.

It is useful for what follows to give a brief description of the variational framework used in ^[4]. Recalling the assumption $(*)$, solutions of (2.1)–(2.3), which are not "one dimensional", have been searched as minima of the (renormalized) functional

on the set

Using Fubini Theorem, since $F$ depends only on the variable $x$, the functional ${{\varphi}}$ can be written in the more enlighting form

which reveals the Lagrangian structure of the problem. The cyclic variable $y$ plays the role of an evolution variable and the elements $u\in\Gamma_{2, j}$ can be seen as test trajectories, $y\mapsto u(\cdot, y)\in\Gamma$, connecting two different minimal sets, ${{\cal K}}_{0}$ and ${{\cal K}}_{j}$, of the "potential" $V(u(\cdot, y)) -c$.

This point of view led in ^[4] to the use of minimization techniques in the spirit of earlier papers on the heteroclinic problem for Hamiltonian systems and PDE (see ^[3,50,51]) to show that at least for two different values of $j\in {{\bf Z}}\setminus\{0\}$, ${{\varphi}}$ attains the minimum in ${{\Gamma}}_{2, j}$. After ^[52], we know that the ordered structure of ${{\cal K}}$ implies that the values of $j$ have to be equal to $\pm 1$ and the solutions found in ^[4] are in fact elements of the set ${{\cal M}}_{1}$ described above.

Note that, both for a single equation with nonlinearities $F$ depending only on the variable $x_{1}$ as in ^[4] and for the case of autonomous systems as in ^[1,55], the set ${{\cal M}}_{1}$ of minimal double heteroclinic connections is invariant with respect to $y$ translations. Hence ${{\cal M}}_{1}$ has not "gap-like" properties and one cannot hope to use the arguments in ^[52,53] to obtain further solutions (like higher dimensional connections or multitransition type solutions) of this kind of problems.

Pursuing the study of the case $F = F(x_{1}, u)$, a different method, based on Hamiltonian identities due the conservation of the energy conjugated to the cyclic variable $y$, was then developed in ^[6] showing that, when $(*)$ holds, (2.1)–(2.3) has other (infinitely many) two dimensional solutions, heteroclinic or homoclinic in the variable $y$ to (locally minimal) solutions of (2.4) not belonging to ${{\cal K}}$. The method was refined and adapted in ^[8] to show the existence of infinitely many other solutions to (2.1)–(2.3), called brake orbit type solutions, which have a periodic behaviour in the variable $y$ (see also ^[7] where the case of a potential $F = F(x_{1}, u)$ depending in an almost periodic way on $x_{1}$ is studied). The same approach was used by F. Alessio in ^[2] to obtain analogous multiplicity results for the problem (2.5)–(2.6), relative to the Allen Cahn type systems considered in ^[1]. In ^[12] we finally relaxed the symmetric assumption ($F_{2}$) obtaining the same kind of solutions in the asymmetric setting considered by M. Schatzman in ^[55].

We give here below a brief illustration of these "energy constrained" methods describing with some details the main ideas in the setting studied in ^[2].

The fist step in ^[2] is to weaken the finiteness assumption $(**)$ on the minimal set ${{\cal K}}_{s} = \{q\in\Gamma_{s}\mid V(q) = c\equiv\inf_{\Gamma_{s}}V\}$ made in ^[1]. Indeed, in analogy with the assumption $(*)$ in ^[4], in ^[2] a weak separation property on ${{\cal K}}_{s}$ is considered:

In Theorem 1.1 of ^[2], a first strenghtening of the result in ^[1] is given showing that if ($F_{1}$) ($F_{2}$) and ($*_{c}$) are satisfied then the problem (2.5)–(2.6) admits a bidimensional solution $U\in C^{2}(\mathbb{R}^{2}, \mathbb{R}^{2})$ satisfying

As in ^[4] this solution is obtained as a minimizer of the renormalized functional

Note that ${{\varphi}}$ is well defined and not negative on the space

Since $\varphi(q) = 0$ for all $q\in {{\cal K}}_{s}$, the elements of ${{\cal K}}_{s}$ are global minimizers of ${{\varphi}}$ on ${\cal H}$. The bidimensional solution satisfying (2.9) is obtained by minimizing ${{\varphi}}$ on the space

Roughly, the element in ${{\cal H}}$ can be seen as trajectories $y\in \mathbb{R}\mapsto u(\cdot, y)\in \Gamma_{s}$ (continuous with respect to the $L^{2}(\mathbb{R}, \mathbb{R}^{2})$ metric) and the bidimensional solution $U$ as a minimal trajectory in ${{\cal H}}_{c}$ satisfying the infinite dimensional gradient system

The one dimensional action $V$ plays the role of a potential in (2.10) and its minimal sets, ${{\cal K}}^{\pm}$, are constituted by equilibria of the equation. Then $U$ is an heteroclinic connection between the two sets.

The new step is now to observe (as done analogously in ^[6,7,8]) that since (2.10) is autonomous, an energy is conserved along its trajectories. More precisely, by Lemma 4.3.10 in ^[2], if $u\in{\cal H}$ solves $(2.5)$ on $\mathbb{R}\times (y_{1}, y_{2})$ then

is constant on $(y_{1}, y_{2})$ (see ^[41] for more general identities of this kind). In particular $E_{U}(y) = -c$ for every $y\in \mathbb{R}$ and a different way to characterize the solution $U$ is as a solution with energy equal to $-c$ connecting as $y\to\pm\infty$ the disjoint subsets ${{{\cal K}}}_{\pm}$ of the level set $\{q\in\Gamma\, |\, V(q)\leq c\}$.

The idea is to look for new solutions by varying the value of the energy and looking for solutions connecting disjoint subsets of the correponding sublevel of the potential. Indeed if $\lambda > 0$ is small enough, by $(*_{c})$ we obtain that for any $b\in(c, c+\lambda)$,

The second problem considered in ^[2] is to show that when $(*_{b})$ holds, there are solutions $u\in{\cal H}$ to (2.5) with Energy $E_{u} = -b$ and "connecting" the sets ${{\cal V}}_-^{b}$ and ${{\cal V}}_+^{b}$. The basic remark in the argument is that if $u$ is such a solution then

and the condition $V(u(\cdot, y))\geq b$ becomes a natural constraint in such a problem. Then, in ^[2] these solutions are searched by minimizing the new renormalized functional

on the space

Note that, differently for the minimum problem for ${{\varphi}}_{c}$ on ${{\cal H}}_{c}$, when $b > c$, minimizing ${{\varphi}}_{b}$ on ${{\cal H}}_{b}$ is a constrained problem. The advantage to require $V(u(\cdot, y))\geq b$ for $y\in \mathbb{R}$ is that this allows to say that ${{\varphi}}_{b}$ is well defined and positive on ${{\cal H}}_{b}$. On the other hand, if $u$ is a minimum of ${{\varphi}}_{b}$ on ${{\cal H}}_{b}$ we have that $u$ solves the equations in (2.5) on a strip $\mathbb{R}\times (y_{1}, y_{2})$ only when the constraint $V(u(\cdot, y))\geq b$ is satified with a strict inequality on $(y_{1}, y_{2})$.

In ^[2] it is shown the existence of a minimizing sequences of $\varphi_{b}$ on ${\cal H}_{b}$ weakly convergent to a function $u_{b}\in{\cal H}$ for which there exists a transition interval $(\sigma_{b}, \tau_{b})\subset \mathbb{R}$ such that

(1) if $[y_{1}, y_{2}]\subset (\sigma_{b}, \tau_{b})$ then $\inf_{y\in[y_{1}, y_{2}]}V(u_{b}(\cdot, y)) > b$,

(2) $\liminf_{y\to \sigma_{b}^{+}}{{\mathrm{dist}}}_{L^{2}(\mathbb{R}, \mathbb{R}^{2})}(u_{b}(\cdot, y), {{\cal V}}^{b}_{-}) = \liminf_{y\to \tau_{b}^{-}}{{\mathrm{dist}}}_{L^{2}(\mathbb{R}, \mathbb{R}^{2})}(u_{b}(\cdot, y), {{\cal V}}^{b}_{+}) = 0$.

By (1), the minimality property of $u_{b}$ guarantees that $u_{b}$ satisfies the equations in (2.5) on $\mathbb{R}\times (\sigma_{b}, \tau_{b})$. By regularity, using (2), one recovers that $V(u_{b}(\cdot, y))\to b$ whenever $y\to \sigma_{b}^{+}$ or $y\to \tau_{b}^{-}$. Again the minimality property of $u_{b}$ gives that $E_{u_{b}} = -b$ for all $y\in(\sigma_{b}, \tau_{b})$ and so that

If $\sigma_{b} = -\infty$ and $\tau_{b} = +\infty$, $u_{b}$ is actually a solution of (2.5)–(2.6) connecting by (2) the sets ${{\cal V}}^{b}_{\pm}$. When $\sigma_{b}\in \mathbb{R}$ or $\tau_{b}\in \mathbb{R}$, it is possible to extend $u_{b}|_{ \mathbb{R}\times [\sigma_{b}, \tau_{b}]}$ on $\mathbb{R}^{2}$ by reflection in the variable $y$ with respect to $\sigma_{b}$ or $\tau_{b}$ and then by periodic continuation. By (2.11) one again obtains a solution $v_{b}$ of (2.5)–(2.6) connecting ${{\cal V}}^{b}_{\pm}$ with energy equal to $-b$.

The behaviour of these solutions can be characterized more precisely depending on the boundedness properties of the transition interval $(\sigma_{b}, \tau_{b})$.

When $\sigma_{b} = -\infty$ (resp. $\tau_{b} = +\infty$), in ^[2] it is shown that the $\alpha$-limit (resp. $\omega$-limit) of $u_{b}$ is a set ${{\cal K}}_{-}(b)\subset {{\cal V}}^{b}_{-}$ (resp. ${{\cal K}}_{+}(b)\subset {{\cal V}}^{b}_{+}$) of {critical points} of $V$ at level $b$ and in particular $b$ is a critical value of ${{V}}$.

Then, if $\sigma_{b} = -\infty$ and $\tau_{b} = +\infty$ we have that $v_{b} = u_{b}$ is a solution of heteroclinic type connecting ${{\cal K}}_{\pm}(b)$ as $y\to \pm\infty$.

If $\sigma_{b} = -\infty$ and $\tau_{b}\in \mathbb{R}$, $v_{b}$ is equal to $u_{b}$ on $\mathbb{R}\times (-\infty, \tau_{b}]$ and symmetric in the variable $y$ with respect to $\tau_{b}$. It defined a homoclinic type solution of (2.5)–(2.6) which emanates from ${{\cal K}}_{-}(b)$ as $y\to-\infty$, reachs ${{\cal V}}^{b}_{+}$ for $y = \tau_{b}$ and then symmetrically returns to ${{\cal K}}_{-}(b)$ as $y\to+\infty$. Analogously, when $\sigma_{b}\in \mathbb{R}$ and $\tau_{b} = +\infty$, $v_{b}$ is a solution to (2.5)–(2.6) homoclinic to ${{\cal K}}_{+}(b)$ and symmetric with respect to $y = \sigma_{b}$.

Finally, if both $\sigma_{b}, \tau_{b}\in \mathbb{R}$, $v_{b}(x, y)$ is equal to $u_{b}$ on $\mathbb{R}\times [\sigma_{b}, \tau_{b}]$ being symmetric in $y$ with respect to both $\sigma_{b}$ and $\tau_{b}$, and so periodic, with period $T_{b} = 2(\tau_{b}-\sigma_{b})$. We say that $v_{b}$ is a brake orbit type solution of (2.5)–(2.6) defining a periodic trajectory of period $T_{b}$ which oscillates back and forth in ${{\cal H}}$ along a simple curve connecting the two turning points $v_{b}(\cdot, \sigma_{b})\in{{\cal V}}^{b}_{-}$ and $v_{b}(\cdot, \tau_{b})\in{{\cal V}}^{b}_{+}$.

By the above observations, when $b$ is a regular value of $V$, the corresponding solution has to be of brake orbit type. As in Lemma 4.2.9 in ^[8], as a consequence of the Sard Smale Theorem, it can be proved that the set of regular values of $V$ is open and dense in $[c, c+\lambda)$. In this sense we can say that generically for $b\in [c, c+\lambda)$ the corresponding solution is periodic in $y$, of the brake orbit type. If otherwise $b\in [c, c+\lambda)$ is a critical value of $V$, then the corresponding connecting orbit may exhibit homoclinic or heteroclinic behaviour.

We refer to the paper with A. Zuniga ^[13] where the above described "constrained energy method" is applied to obtain analogous classes of connecting type solutions in the simpler context of ODE gradient systems of the form

including applications to classical cases as double well, Duffing or pendulum like potentials.

Other more recent papers obtained multiplicity results regarding periodic solutions for Allen Cahn systems or different type of equations with related but different methods, based again on the Lagrangian structure of the problem. We quote the nice papers by G. Fusco, G. F. Gronchi, M. Novaga ^[23], A. Cesaroni and M. Cirant ^[21], A. Monteil, F. Santambrogio ^[47] and the reference therein. In particular in ^[47] a general study on the geodesic problem in metric space is done. As an application the result in ^[1] is recovered and the heteroclinic connection between two isolated minima $q_{\pm}$ of $V$ is obtained as a minimal geodesic relative to the Maupertius Jacobi distance

Here $\Gamma(z^{-}, z^{+})$ is the set of path $\gamma:[0, 1]\to\Gamma_{s}$ which are piecewise locally absolutely continuous with respect to the $L^{2}(\mathbb{R}, \mathbb{R}^{2})$ metric (or, by density, the $W^{1, 2}(\mathbb{R}, \mathbb{R}^{2})$ metric) with $\gamma(0) = z^{-}$ and $\gamma(1) = z^{+}$. For the use of the Maupertius principle in the study of the periodic or the heteroclinic problem for gradient ODE systems we refer to the paper by V. Benci ^[15] and the one by P. Sternberg and A. Zuniga ^[57].

To end this section we only briefly mention for the interested readers the papers ^[9] and ^[10] where the problem of finding solutions depending on more than two variables was studied, with different methods, both for the problem with $F = F(x_{1}, u)$ considered in ^[4] or the system case considered in ^[1].

3.   Brake orbits type solutions for NLS

In this Section we describe some applications of the above illustrated methods to non linear Schrödinger equations. Even if the geometry of the problem is in this case very different with respect to the one relative to the Allen Cahn models, as done in ^[11] the constrained energy method applies also in this context to find and characterize families of connecting orbit type solutions, at least for a restricted range of values of the exponent $p$.

In ^[11] we studied equations of the form

where $N\geq 1$ and the nonlinearity $f$ is modeled on the power case $f(v) = |v|^{p-1}v$ with $p+1$ subcritical and greater than $2$. This kind of equations is widely used in physical models, in particular in the study of standing waves solutions of the corresponding nonlinear Schrödinger type equations (see ^[18]).

The problem of finding positive solutions $v\in H^{1}(\mathbb{R}^{N+1})$ of (E) has been deeply studied and the existence of radial solutions was first obtained by W. A. Strauss in ^[58]. Nearly optimal existence results of least energy solutions for (E) was given by H. Berestycki and P. L. Lions in ^[18] (see also ^[19]). In the pure power case, uniqueness and non degeneracy properties of solutions of (E) in $H^{1}(\mathbb{R}^{N+1})$ was derived by M. K. Kwong in ^[44] and by J. Serrin and M. Tang for more general nonlinearity in ^[56].

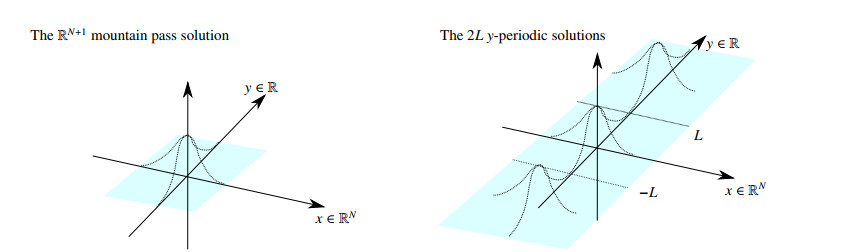
In the seminal work by N. Dancer, ^[22], it is studied a new class of entire solutions of (E) in the pure power case. The starting idea is to see the ground state solution $u_{0}(x)$ of (E) in $\mathbb{R}^{N}$ (a mountain pass type solution) as a solution on $\mathbb{R}^{N+1}$, constant with respect to the $y$ variable. In the pure power case, when the ground state is nondegenerate, Dancer used bifurcation and continuation arguments to get the existence of a continuous branch of entire positive solutions of (E) in $\mathbb{R}^{N+1}$ bifurcating from the cylindric type solution $u_{0}$. These solutions are periodic in the variable $y$ and decay to zero as $|x|\to+\infty$. See Figure 2.

Analogous periodic solutions were found and used, again in the pure power case, as prescribed asymptotes in the constructions of multiple ends solutions by A. Malchiodi in ^[45]. These periodic solutions have large periods and, differently from the Dancer result, emanate via the Implicit Function Theorem, from the mountain pass solutions of (E) in $\mathbb{R}^{N+1}$. See Figure 3.

Different qualitative properties of positive solutions $v(x, y)$ of $(E)$ which decay to zero as $|x|\to+\infty$, such as radial symmetry with respect to the variable $x$, have been described by C. Gui, A. Malchiodi and H. Xu in ^[42] and by A. Farina, A. Malchiodi and M. Rizzi in ^[36]. In these studies, based on moving plane techniques, is again involved the use of Hamiltonian identities, such as a conservation of energy along the cylindrical variable $y$.

Indeed, as in the preceding section for the Allen Cahn models, prescribing the decay properties of a solution only with respect to the variable $x\in \mathbb{R}^{N}$, naturally gives to $y$ the role of an evolution variable. The periodic solutions described above belong to the space

and in analogy with (2.10)verify (at least in a weak sense) the Newtonian evolution equation

In (3.2), $V'$ is the gradient of the Euler functional relative to the problem in $\mathbb{R}^{N}$,

where $F(s) = \int_{0}^{s}f(t)\, dt$. We name layered solution any $v\in{{\cal H}}$ which solves (E).

The Eq (3.2) has a Lagrangian structure and the functional $U = -V$ plays the role of the energy potential. In this connection, any $u\in H^{1}(\mathbb{R}^{N})$ which solves (E) is an equilibrium of (3.2) and the Dancer's or Malchiodi's solutions are periodic orbits of the system. As for the Allen Cahn models, if $v$ is a layered solution then the Energy function

is constant.

In ^[11], we applied the constrained energy method to find connecting orbit type layered solution of (E) with prescribed energy. This was done under slightly general assumptions on the non linearity $f$. It was assumed that

$(f1)$ $f\in C^1(\mathbb{R})$,

$(f2)$ there exists $C > 0$ and $p\in(1, 1+\tfrac{4}{N})$ such that $|f(t)|\le C(1+|t|^{p})$ for any $t\in \mathbb{R}$,

$(f3)$ there exists $\mu > 2$ such that $0 < \mu F(t)\le f(t)t$ for any $t\ne 0$, where $F(t) = \int_0^t f(s)\, ds$,

$(f4)$ $f(t)t < f'(t)t^{2}$ for any $t\ne 0$.

By $(f1) - (f4)$ the above defined functional $V\in C^{1}(H^{1}(\mathbb{R}^{N}))$ and satisfies the geometrical assumptions of the mountain pass Theorem. Considering the mountain pass level

where

we have that $c > 0$ is an asymptotical critical level for $V$. As it is well known $c$ is the lowest positive critical level of $V$ (see ^[43]). Using the definition of the mountain pass level, the assumptions on $f$ are sufficient to show that for any $b\in [0, c)$ the sublevel set $\{u\in H^{1}(\mathbb{R}^{N})\mid V\leq b\}$ splits into the disjoint union of two connected nonempty subsets:

where ${\cal V}^{b}_{-}$ denotes the component which contains $0$. In ^[11] we adapt the constrained energy method described in the previous section to obtain for any $b\in [0, c)$, layered solution $v_{b}$ of (E) with energy $E_{v_{b}} = -b$ "connecting" the sets ${\cal V}^{b}_{\pm}$. Since, as remarked above, $c$ is the lowest positive critical level of $V$, any $b\in (0, c)$ is a regular value of $V$ and as discussed in the previous section, the corresponding solution $v_{b}$ is a {brake orbit type} periodic layered solution of (E). Theorem 1.1 in ^[11] precisely states the following

Theorem 3.1. ^[11] If $f$ satisfies $(f1)-(f4)$ then for any $b\in [0, c)$ the equation (E) has a solution $v_{b}\in C^{2}(\mathbb{R}^{N+1})$ with energy $E_{v_{b}} = -b$ and such that

(i) $v_{b} > 0$ on $\mathbb{R}^{N+1}$,

(ii) $v_{b}(x, y) = v_{b}(|x|, y)\to 0$ as $|x|\to+\infty$, uniformly w.r.t. $y\in \mathbb{R}$,

(iii) $\partial_{r}v_{b}(x, y) < 0$ for $r = |x| > 0$ and $y\in \mathbb{R}$.

Moreover, if $b > 0$,

(iv) there exists $T_{b} > 0$ such that $v_{b}$ is periodic of period $2T_{b}$ in the variable $y$ and symmetric with respect to $y = 0$ and $y = T_{b}$.

(v) $\partial_{y}v_{b}(x, y) > 0$ on $\mathbb{R}^{N}\times (0, T_{b})$, $v_{b}(\cdot, 0)\in{{\cal V}}^{b}_{-}$, $v_{b}(\cdot, T_{b})\in{{\cal V}}^{b}_{+}$.

Finally, if $b = 0$,

(vi) $v_{0}\in H^{1}(\mathbb{R}^{N+1})$ is radially symmetric and $\partial_{r}v_{0} < 0$ for $r = |(x, y)| > 0$,

(vii) $v_{0}(\cdot, 0)\in{{\cal V}}^{0}_{+}$ and $v_{0}$ is a mountain pass point of the Euler funcional relative to (E) on $H^{1}(\mathbb{R}^{N+1})$.

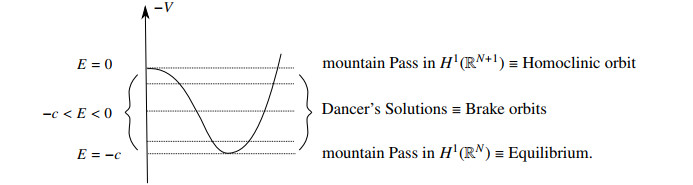
Theorem 3.1 provides for any $b\in [0, c)$ a positive layered solution $v_{b}$ to (E) with energy $-b$. With respect to the variable $x$ it is radially symmetric and decay to $0$ as $|x|\to+\infty$ uniformly with respect to $y\in \mathbb{R}$. When $b > 0$ the solution $v_{b}$ is a periodic solution of period $2T_{b}$ which is symmetric with respect to $y = 0$ and $y = T_{b}$ and has the beaviour of a brake orbit type solution. Its trajectory $y\to v_{b}(\cdot, y)\in H^{1}(\mathbb{R}^{N})$ oscillates back and forth along a simple curve connecting the two turning points $v_{b}(\cdot, 0)\in{\cal V}^{b}_{-}$ and $v_{b}(\cdot, T_{b})\in{\cal V}^{b}_{+}$. These solutions are clearly related to the Dancer's and Malchiodi's solutions. When $b = 0$ the solution $v_{0}$ belongs to $H^{1}(\mathbb{R}^{N+1})$ and defines a homoclinic type layered solution to $0\in H^{1}(\mathbb{R}^{N})$. By (Vii), $v_{0}$ is a mountain pass point of the Action functional to (E) on $H^{1}(\mathbb{R}^{N+1})$. On the other hand the mountain pass point of $V$ in $H^{1}(\mathbb{R}^{N})$ is an equilibrium of (3.2) at energy $-c$. The Energy diagram in Figure 4 wish to summarize these considerations.

The application of the constrained energy method in this case is much more complicated than that for the Allen Cahn models, due to strong lack of compactness and weak semicontinuity of the problem. This comes from the competition among the terms $\|u\|_{H^{1}(\mathbb{R}^{N})}^{2}$ and $\int_{ \mathbb{R}^{N}}F(u)$ which enter in the potential ${{V}}(u)$ with different sign and explains why we assume in $(f2)$ that $p < 1+4/N$.

The exponent $p = 1+4/N = 2_{G, N}-1$, where $2_{G, N}$ has different critical properties due to the Gagliardo Niremberg inequalities (see ^[39,49]), see (4.7) and the related observations in the next section. We recall that $2_{G, N}$ is critical for the minimum problem $\inf\{{{V}}(u)\, |\, u\in H^{1}(\mathbb{R}^{N}), \, \|u\|_{L^{2}(\mathbb{R}^{N})} = 1\}$ and with respect to the property of orbital stability of the solutions of (E) in $H^{1}(\mathbb{R}^{N})$. The ground state solution of (E) in $H^{1}(\mathbb{R}^{N})$ is stable if and only if $p+1\in(2, 2_{G, N})$, see ^[17,20,59].

When $p+1 < 2_{G, N}$ the functional $V$ exhibits the coerciveness and semicontinuous properties sufficient to recover some of the basic properties used applying the constrained energy method for the Allen Cahn model. In particular note that the exponent $2_{G, N}$ is critical with respect to the separation of the sets ${{\cal V}}^{b}_{\pm}$ with respect to the $L^{2}(\mathbb{R}^{N})$ metric (see proposition 1 in the next section). Assuming $p+1 < 2_{G, N}$ leads to a situation like the one in ($*_{b}$) for the Allen Cahn models where an $L^{2}$ separation between the sets ${{\cal V}}^{b}_{\pm}$ is used.

We think however that the condition $p+1 < 2_{G, N}$ is only technical and that a refined analisys can lead to apply the constrained energy method to cover all the subcritical cases $2 < p+1 < 2^{*}_{N+1}$ (where as usual we denote the critical Sobolev exponent $2^{*}_{n} = 2n/(n-2)$ for $n > 2$ and $2^{*}_{n} = +\infty$ for $n = 1, 2$). This will be the object of future studies. In the next section, as a fist step in this program, we characterize the metric separation properties of the sets ${{\cal V}}^{b}_{\pm}$ in relation to the value of the exponent $p+1\in (2, 2^{*}_{N})$.

4.   Metric separation properties of sublevels of $V$ below the MP level

A basic point in applying the constrained energy method to look for layered solutions of (E) connecting the sets ${{\cal V}}^{b}_{\pm}$, is to well understand how and with respect to which metrics the sets ${{\cal V}}^{b}_{\pm}$ are separated, depending on the values of the exponent $p$. The present more technical section is devoted to study this problem. This will be done relatively to the $L^{2}(\mathbb{R}^{N})$ distance and a Jacobi type metric (see (2.12) for the Allen Cahn model), which are naturally related with the constrained energy approach. In fact we show that while ${{\mathrm{dist}}}_{L^{2}(\mathbb{R}^{N})}({{\cal V}}^{b}_{-}, {{\cal V}}^{b}_{+}) > 0$ if and only if $p+1\leq 2_{G, N}$ we have that the two sets have positive Jacobi distance $d_{J}({{\cal V}}^{b}_{-}, {{\cal V}}^{b}_{+})$ (see (4.19)) if and only if $p+1\leq 2^{*}_{N+1}$. For the sake of simplicity we will do this study in the power case $F(u) = \tfrac 1{p+1}|u|^{p+1}$.

4.1.   The functional $V$

We assume $N\geq 1$ and $1 < p < 2^{*}_{N}-1$ when $N > 1$ while $p > 1$ if $N = 1$. We work on the space of radially symmetric functions

endowed with its standard norm and scalar product

For $q\geq 1$ we denote with $\|u\|_{q}$ the usual norm of the function $u$ in the space $L^{q}({ \mathbb{R}^N})$. We recall that by the Strauss Lemma (see ^[58]) $X$ is compactly embedded in $L^{q}(\mathbb{R}^{N})$ for $q\in (2, 2^{*}_{N})$.

We study the functional

As it is well known ${{V}}\in C^1(X, \mathbb{R})$ with

Thanks to the compact embedding of $X$ in $L^{p+1}(\mathbb{R}^{N})$ and the weakly semicontinuity of the $L^2$-norm, the functional ${{V}}$ is weakly semicontinuous on $X$. In fact, we have

Lemma 4.1. Let $u_{n}\to u$ and $v_{n}\to v$ weakly in $X$. Then

$(i)$ $\lim_{n\to+\infty}\int_{ \mathbb{R}^{N}} |u_{n}(x)|^{p+1}dx = \int_{ \mathbb{R}^{N}} |u(x)|^{p+1}dx$

$(ii)$ $\lim_{n\to+\infty}\int_{ \mathbb{R}^{N}} |u_{n}(x)|^{p-1}u_{n}(x)v_{n}(x)\, dx = \int_{ \mathbb{R}^{N}} |u(x)|^{p-1}u(x)v(x)\, dx$

In particular ${{V}}(u)\leq\liminf_{n\to+\infty}{{V}}(u_{n})$ and ${{V}}'(u)h = \lim_{n\to+\infty}{{V}}'(u_{n})h$ for any $h\in X$.

4.2.   The mountain pass geometry

As it is well known, the functional $V$ satisfies the geometrical hypotheses of the mountain pass theorem. Indeed, since $p+1 < 2^{*}_{N}$, by the Sobolev immersion Theorem we have

and so

In particular there exists $\rho > 0$ such that

Moreover, if $u\in X\setminus\{0\}$ then

Defining

and $c = \inf_{{{\gamma}}\in\Gamma}\max_{s\in[0, 1]}{{V}}({{\gamma}}(s))$, by the mountain Pass Theorem we infer that $c\geq \tfrac 14\rho^{2}$ and that there exists a Palais Smale sequence for ${{V}}$ at level $c$. Since

the Palais Smale sequences of ${{V}}$ are bounded in $X$. Another plain consequence of (4.3) is that

The existence of a critical point of $V$ at level $c$ is then easily deduced.

Theorem 4.1. There exists $u_{0}\in X\setminus \{0\}$ such that ${{V}}'(u_{0}) = 0$ and ${{V}}(u_{0}) = c$.

Proof. By the mountain Pass Theorem and (4.3) there exists a bounded sequence $\{u_n\}\subset X$ such that ${{V}}(u_{n})\to c$ and ${{V}}'(u_{n})\to 0$. Up to subsequence, $u_{n}\to u_{0}$ weakly in $X$. By Lemma 4.1 we deduce that ${{V}}'(u_{0}) = 0$ and ${{V}}(u_{0})\leq c$. To show that ${{V}}(u_{0}) = c$ observe that ${{V}}'(u_{n})u_{n}\to 0$ and $\|u_{n}\|_{p+1}\to\|u_{0}\|_{p+1}$ imply $\|u_{n}\|^{2}\to \|u_{0}\|_{p+1}^{p+1}$. Since ${{V}}'(u_{0})u_{0} = 0$ we also have $\|u_{0}\|^{2} = \|u_{0}\|_{p+1}^{p+1}$. Then $\|u_{n}\|^{2}\to \|u_{0}\|^{2}$ and so ${{V}}(u_{n})\to \tfrac 12\|u_{0}\|^{2}-\tfrac 1{p+1}\|u_{0}\|^{p+1}_{p+1} = {{V}}(u_{0})$. Hence ${{V}}(u_{0}) = c$.

4.3.   Sublevels of ${{V}}$

We characterise here some properties of the sublevel sets

for level values $b\in [0, c)$.

We will make use of the Gagliardo Nirenberg inequalities (see ^[39,49]) which in particular imply

where $K_{G} > 0$ and

By (4.5) the functional $V$ has good coercivity properties on the bounded sets of $L^{2}(\mathbb{R}^{N})$ when $p+1 < 2_{G, N}$ where we set

Indeed by (4.6), if $p+1 < 2_{G, N}$ then

Then, by (4.5) and (4.8) we obtain that if $\|\nabla u_{n}\|_{2}\to+\infty$ and $\|u_{n}\|_{2}\leq C < +\infty$ then

It is useful to describe the behaviour of $V$ along the rays in $X$ starting from the origin.

Lemma 4.2. For any $u\in X\setminus\{0\}$ setting $t_{u} = \left(\tfrac{\|u\|^{2}}{\|u\|_{p+1}^{p+1}}\right)^{\frac 1{p-1}}$ we have $V'(t_uu)u = 0$ and

Moreover, for $u\in X\setminus\{0\}$ we have

Proof. The first part of the lemma is obtained since ${{V}}(tu) = \frac 12 t^{2}\|u\|^{2}-\frac{t^{p+1}}{p+1}\|u\|_{p+1}^{p+1}$ and so $\tfrac d{dt} {{V}}(t u) = t(\|u\|^{2}-t^{p-1}\|u\|_{p+1}^{p+1})$ for any $t\geq 0$. To derive the equality in (4.10) it is enough to perform the computation:

Finally the inequality in (4.10) follows by (4.5)–(4.6), which imply

and the Lemma is proved.

Remark 4.1 By continuity and Lemma 4.2, for any $u\in X\setminus\{0\}$ and $b\in [0, c)$, there exist unique ${{\alpha_{u, b}}}\in (0, t_{u})$ and ${{\omega_{u, b}}}\in (t_{u}, +\infty)$ such that ${{V}}({{\alpha_{u, b}}} u) = {{V}}({{\omega_{u, b}}} u) = b$. Note that ${{\alpha_{u, b}}}$ is strictly increasing and ${{\omega_{u, b}}}$ strictly decreasing for $b\in [0, c)$. By definition ${{V}}(\omega_{u, 0}u) = \omega_{u, 0}^{2}(\tfrac 12\|u\|^{2}-\tfrac 1{p+1}\omega_{u, 0}^{p-1}\|u\|^{p+1}_{p+1}) = 0$. Hence

and so for any $b\in [0, c)$ we have

Hence, nothing that $\frac{d}{ds}V(su) = V'(su)u$, for any $b\in [0, c)$, if $u\in X\setminus\{0\}$, there results that if $t\in(0, \alpha_{u, b}]\subset(0, t_u)$ then $V'(tu)u > 0$ and $V(tu)\le V(\alpha_{u, b}u) = b$. Analogously, if $t\in[\omega_{u, b}, +\infty)$ then $V'(tu)u < 0$ and $V(tu)\le b$. Moreover, if $t\in(\alpha_{u, b}, \omega_{u, b})$, then $V(tu) > b$.

Therefore, if $u\in X\setminus\{0\}$ and $V(u)\le b$, we have either $\alpha_{u, b}\ge 1$ and hence $V'(u)u > 0$, or $\omega_{u, b}\le 1$ from which $V'(u)u < 0$. $

We consider the sublevel sets of ${{\cal V}}$

By definition of the mountain pass level the set ${{\cal V}}^{b}$ is not path connected for any $b\in [0, c)$. Given $b\in [0, c)$, recalling Remark 4.1, we denote

and observe that, by Remark 4.1,

Note for all $b\in [0, c)$ we have $u\in{{\cal V}}^{b}_{-}$ if $1\in(0, {{\alpha_{u, b}}}]$, that is when ${{\alpha_{u, b}}}\geq 1$. Analogously, if ${{\omega_{u, b}}}\leq 1$ then $u\in{{\cal V}}^{b}_{+}$. Hence, by Lemma 4.2 and Remark 4.1, the two sets are characterised as follows

Moreover, again by Remark 4.1, if $b\in (0, c)$ then

while

We consider now the Nehari Manifold associated with $V$

Remark 4.2. Note that, by Lemma 4.2, we have

Hence, by definition, for any $u\in{\cal N}$ we get $V(u) = \max_{t\geq 0}V(tu)$. By the definition of the mountain pass level $c$, this implies that $V(u)\geq c$ for any $u\in {\cal N}$. Moreover, since any nonzero critical point of $V$ belongs to ${\cal N}$, by Theorem 4.1, there exists $u_{0}\in {\cal N}$ such that $V(u_{0}) = c$. Therefore

from which in particular ${\cal N}\cap ({{\cal V}}^{b}_{-}\cup {{\cal V}}^{b}_{+}) = \emptyset$ for any $b\in [0, c)$. $

Remark 4.3. As a complementary property to Remark 4.2 note that for any $b\in [0, c)$ the Nehari Manifold separates ${{\cal V}}_{-}^{b}$ from ${{\cal V}}^{b}_{+}$ in the sense that given any path $\gamma\in C([0, 1], X)$ such that $\gamma(0)\in {{\cal V}}_{-}^{b}$ and $\gamma(1)\in{{\cal V}}^{b}_{+}$, there exists $s_{\cal N}\in (0, 1)$ such that $\gamma(s_{\cal N})\in{\cal N}$.

Indeed, if $\gamma(0)\not = 0$, by (4.12) and (4.13), $V'(\gamma(0))\gamma(0) > 0$ and $V'(\gamma(1))\gamma(1) < 0$, so that the existence of $s_{\cal N}$ follows by the continuity of the function $s\mapsto V'(\gamma(s))\gamma(s)$ on $[0, 1]$. Otherwise, if $\gamma(0) = 0$, since $\gamma$ is not constant, there exists $s\in (0, 1)$ such that $0 < \|\gamma(s)\| < \rho$ and so, by (4.2), $V'(\gamma(s))\gamma(s)\ge\frac12\|\gamma(s)\| > 0$. Then, the existence of $s_{\cal N}$ follows again by continuity since $V'(\gamma(1))\gamma(1) < 0$.

Lemma 4.3. If $b\in [0, c)$ then ${{\cal V}}_{-}^{b}$ and ${{\cal V}}_{+}^{b}$ are weakly closed in $X$.

Proof. Let $A\not = B\in \{{{\cal V}}^{b}_{-}, {{\cal V}}^{b}_{+}\}$. To prove the proposition we consider a sequence $(u_{n})\subset A$ such that $u_{n}\to u_{0}$ weakly in $X$ and we show that $u_{0}\in A$. Since $(u_{n})\subset{{\cal V}}^{b}$ we know that ${{V}}(u_{n})\leq b$. Hence by Lemma 4.1 ${{V}}(u_{0})\leq b$. Then, if we assume by contradiction that $u_{0}\notin A$ we have $u_{0}\in B$. Consider the path $\gamma_{n}(s) = u_{0}+s(u_{n}-u_{0})$, $s\in [0, 1]$. Since $\gamma_{n}(0) = u_{0}\in B$ and $\gamma_{n}(1) = u_{n}\in A$, by Remark 4.3, for any $n\in{{\bf N}}$ we find $s_{n}\in (0, 1)$ such that $\gamma_{n}(s_{n})\in {\cal N}$ and so ${{V}}(\gamma_{n}(s_{n}))\geq c$ by (4.14). Since $(u_{n})$ is bounded in $X$ there exists $C > 0$ such that $\max_{s\in[0, 1]}\|\gamma_{n}(s)\|_{p+1}\leq C$ for any $n\in{{\bf N}}$. Then for any $s\in[0, 1]$ and $n\in{{\bf N}}$, we have

Integrating on $[s_{n}, 1]$ we get

Since the weak convergence in $X$ implies the convergence in $L^{p+1}(\mathbb{R}^{N})$ we have $\langle u_{0}, u_{n}-u_{0}\rangle-C^{p}\|u_{n}-u_{0}\|_{p+1} \to 0$ and the above inequality contradicts $b < c$. Hence the Lemma follows.

Remark 4.4. Note that, by (4.3), if $b\in[0, c)$ and $u\in {{\cal V}}^{b}_{-}$, since ${{V}}'(u)u\geq 0$, then

In particular we obtain that ${{\cal V}}^{b}_{-}$ is bounded in $X$. Then, by Lemma 4.3, ${{\cal V}}^{b}_{-}$ is weakly compact in $X$. In particular, if $(u_{n})\subset{{\cal V}}^{b}_{-}$ is such that $u_{n}\to u_{0}$ with respect to the $L^{2}(\mathbb{R}^{N})$ metric then $u_{0}\in {{\cal V}}^{b}_{-}$ and so ${{\cal V}}^{b}_{-}$ is also closed with respect to the $L^{2}(\mathbb{R}^{N})$ metric.

By the Gagliardo Niremberg inequality (4.5), we obtain

Lemma 4.4. We have $\mathrm{dist}_{L^{2}(\mathbb{R}^{N})}({\cal N}, 0) > 0$ if and only if $p+1\leq 2_{G, N}$.

Proof. Let $u\in X\setminus\{0\}$ and, for $\varepsilon > 0$, denote $u_{\varepsilon}(x) = u(\frac x{\varepsilon})$, $x\in \mathbb{R}^N$. By Lemma 4.2, $t_{u_{\varepsilon}}u_{\varepsilon}\in{\cal N}$ for $t_{u_{\varepsilon}} = (\tfrac{\|u_{\varepsilon}\|^{2}}{\| u_{\varepsilon}\|^{p+1}_{p+1}})^{\tfrac 1{p-1}}$. Since

we obtain

When $p > 2_{G, N}-1 = 1+\frac 4N$ we have $\tfrac N2 -\tfrac 2{p-1} > 0$ and so $\|t_{u_{\varepsilon}}u_{\varepsilon}\|_{2}\to 0$ as $\varepsilon\to 0$. This shows that the set ${\cal N}$ accumulates the point $0$ with respect to the $L^{2}$ metric when $p+1 > 2_{G, N}$.

It remains to show that if $p+1\leq 2_{G, N}$ then $\mathrm{dist}_{L^{2}(\mathbb{R}^{N})}({\cal N}, 0) > 0$. By contradiction assume that there exists $(u_{n})\subset{\cal N}$ such that $\|u_{n}\|_{2}\to 0$ as $n\to +\infty$. By (4.2) we have that $\|u\|\geq\rho$ for any $u\in{\cal N}$ and so, in particular, $\|u_{n}\|\geq \rho$ for any $n\in{{\bf N}}$. Then, since $\|u_{n}\|_{2}\to 0$, we have $\|\nabla u_{n}\|_{2}\geq \rho+o(1)$ as $n\to+\infty$. Hence, since by (4.5) we have

and since $p\leq 1+\frac 4N$ implies $2\ge(p+1)(1-\theta_{N, p})$ (see (4.8)) we obtain

a contradiction.

Then we can give our first separation result.

Proposition 4.1. For any $b\in [0, c)$ we have

Proof. Let $p+1 > 2_{G, N}$. By Remark 4.1, if $b\in [0, c)$ and $u_{\varepsilon}(x) = u(\frac x\varepsilon)$, as in the proof of Lemma 4.4, we obtain $\alpha_{u_{\varepsilon}, b}u_{\varepsilon}\in{{\cal V}}^{b}_{-}, \ \omega_{u_{\varepsilon}, b}u_{\varepsilon}\in{{\cal V}}^{b}_{+}$ and $0\leq\alpha_{u_{\varepsilon}, b} < t_{u_{\varepsilon}} < \omega_{u_{\varepsilon}, b}\leq\tfrac{p+1}2\, t_{u_{\varepsilon}}$. In particular, $\|\alpha_{u_{\varepsilon}, b}u_{\varepsilon}\|_{2}\leq\|\omega_{u_{\varepsilon}, b}u_{\varepsilon}\|_{2}\leq \tfrac{p+1}2\|t_{u_{\varepsilon}}u_{\varepsilon}\|_{2}\to 0$ as $\varepsilon\to0^+$, as proved in (4.15). So, if $p+1 > 2_{G, N}$, then $\mathrm{dist}_{L^{2}(\mathbb{R}^{N})}({{\cal V}}^{b}_{-}, {{\cal V}}^{b}_{+}) = 0$ for any $b\in [0, c)$.

Let now $p+1\leq 2_{G, N}$ and $b\in [0, c)$ and let us show that $\mathrm{dist}_{L^{2}(\mathbb{R}^{N})}({{\cal V}}_{-}^{b}, {{\cal V}}_{+}^{b}) > 0$. Arguing by contradiction, assume there exist $(u_{n})\subset{{\cal V}}^{b}_{-}$ and $(v_{n})\subset{{\cal V}}^{b}_{+}$ such that $\|v_{n}-u_{n}\|_{2}\to 0$. Since ${{\cal V}}^{b}_{-}$ is weakly compact (see Remark 4.4) there exists $\bar u\in {{\cal V}}^{b}_{-}$ such that, up to subsequences, $u_{n}\to \bar u$ weakly in $X$.

We claim that along the same subsequence also $(v_{n})$ is bounded in $X$. If the claim is proved then the Proposition follows. Indeed since $\|v_{n}-u_{n}\|_{2}\to 0$ we have $v_{n}\to \bar u$ weakly in $L^{2}(\mathbb{R}^{N})$ and the boundedness of $(v_{n})$ in $X$ would imply, by uniqueness, $v_{n}\to \bar u$ weakly in $X$. Then, by Lemma 4.3, $\bar u\in{{\cal V}}^{b}_{+}$, contradicting that $\bar u\in{{\cal V}}^{b}_{-}$ and concluding the proof.

To prove that $(v_{n})$ is bounded in $X$ we argue in an indirect way assuming that, along a subsequence, still denoted $v_n$, $\|v_{n}\|\to+\infty$. Since $V(v_{n}) = \tfrac 12 \|v_{n}\|^{2}-\tfrac 1{p+1}\|v_{n}\|^{p+1}_{p+1}\leq b$ we derive $\|v_{n}\|_{p+1}\to+\infty$ too. Since $(u_{n})$ is bounded in $X$, and hence in $L^{p+1}$, we obtain that there exists $\bar n\in{{\bf N}}$ such that if $n\geq \bar n$ then

Analogously, since $\|v_{n}\|\to+\infty$ and $(u_{n})$ is bounded in $X$ we can assume that $\bar n$ is so large that if $n\geq \bar n$ then

Using (4.5), for $n\ge\bar n$, it follows that

Recalling that $\|v_{n}-u_{n}\|_{2}\to 0$ and since $(1-\theta_{N, p})(p+1)\leq 2$ when $p+1\leq 2_{G, N}$ (see (4.7) and (4.8)), the above inequality gives that for $n$ large enought

Hence, for such values of $n$, $V'(v_{n})v_{n} = \|v_{n}\|^{2}-\|v_{n}\|_{p+1}^{p+1}\geq\tfrac 12\|v_{n}\|^{2} > 0$, in contradiction by (4.13) with the assumption $v_{n}\in {{\cal V}}^{b}_{+}$. This proves that $(v_{n})$ is bounded in $X$ and, as explained above, concludes the proof of the Proposition. To study the cases $p+1 > 2_{G, N}$ it is useful to observe that

Lemma 4.5. If $p+1\in (2_{G, N}, 2^{*}_{N})$ and $(u_{n})\subset {\cal N}$ is such that $\|u_{n}\|_{2}\to 0$ then $\|\nabla u_{n}\|_{2}\to+\infty$.

Proof. By Lemma 4.4.4 the Nehari manifold ${\cal N}$ accumulates the origin in $X$ when $p+1\in (2_{G, N}, 2^{*}_{N})$. By (4.10) we have that if $u\in {\cal N}$ then

In particular if $(u_{n})\in {\cal N}$ is such that $\|u_{n}\|_{2}\to 0$, since by (4.2) $\|u_{n}\|\ge \rho$, and $\frac{2(p+1)}{p-1} > N$ when $p+1 < 2^{*}_{N}$, we obtain

Since $u_{n}\in{\cal N}$ we have $\|\nabla u_{n}\|_{2}^{2} = \|u_{n}\|_{p+1}^{p+1}$ and so

and the Lemma follows.

Note that if $u\in{\cal N}$, since $\|\nabla u\|^{2}_{2} = \|u\|^{p+1}_{p+1}$, (4.5) implies

and so

Hence, setting

we get

Note that

Lemma 4.4 states that when $p+1 > 2_{G, N}$ there are sequences $(u_{n})$ in ${\cal N}$ such that $\|u_{n}\|_{2}\to 0$ and, by Lemma 4.5, $\|\nabla u_{n}\|_{2}\to+\infty$. By (4.16), we get that in such cases

We have furthermore

Lemma 4.6. Let $p+1\in (2_{G, N}, 2^{*}_{N+1}]$. If $u_{0}\in {\cal N}$ and $u\in X$ are such that

then

Proof. Consider first the case $\|u\|\geq \|u_{0}\|$. Since $u_{0}\in {\cal N}$ and $V'(u)u\geq 0$ we have $\|u_{0}\|^{2} = \|u_{0}\|^{p+1}_{p+1}$ and $\|u\|^{2}\geq \|u\|^{p+1}_{p+1}$. Hence $V(u_{0}) = (\tfrac 12-\tfrac 1{p+1})\|u_{0}\|^{2}$ and $V(u)\geq (\tfrac 12-\tfrac 1{p+1})\|u\|^{2}$, from which

Let now assume $\|u\| < \|u_{0}\|$. By (4.5) we have

Since $\|u\| < \|u_{0}\|$, we have $\|\nabla u-\nabla u_{0}\|_{2}\leq \|u-u_{0}\|\leq 2\|u_{0}\|$. Thus, since $\|u-u_{0}\|_{2}\leq (\tfrac 1{4K_{G}})^{\frac {1}{\theta_{N, p}}}\tfrac 1{\|u_{0}\|^{\sigma_{N, p}}}$, by (4.18) we obtain

Hence, recalling that $\| u_{0}\|_{p+1} = \| u_{0}\|^{2/(p+1)}$ being $u_{0}\in{\cal N}$, we get

But $V'(u)u\geq 0$ implies $\|u\|^{2}\geq \|u\|^{p+1}_{p+1}$ and moreover $V(u_{0}) = (\tfrac 12-\tfrac 1{p+1})\|u_{0}\|^{p+1}_{p+1}$ since $u_{0}\in{\cal N}$. Then

and the Lemma follows.

We have seen in Corollary 2.1 that ${{\cal V}}_{-}^{b}$ and ${{\cal V}}_{+}^{b}$ have zero $L^{2}(\mathbb{R}^{N})$ distance when $p+1 > 2_{G, N}$. Lemma 4.6 allows us to show, as a final result, that the two sets are instead well separated when $2_{G, N} < p+1\leq 2^{*}_{N+1}$ with respect to the Jacobi distance

where

Proposition 4.2. If $b\in [0, c)$ then

Proof. Consider first the case $p+1\in (2^{*}_{N+1}, 2^{*}_{N})$, and so $N > 1$. As in Proposition 4.1 we show that $d_{J}({{\cal V}}_{-}^{b}, {{\cal V}}^{b}_{+}) = 0$ by using dilation. For $u\in X\setminus\{0\}$ and $\varepsilon > 0$ we set $u_{\varepsilon}(x) = u(\frac x{\varepsilon})$. By Lemma 4.2, $t_{u_{\varepsilon}}u_{\varepsilon}\in{\cal N}$ for $t_{u_{\varepsilon}} = (\tfrac{\|u_{\varepsilon}\|^{2}}{\| u_{\varepsilon}\|^{p+1}_{p+1}})^{\tfrac 1{p-1}}$ and by Remark 4.1, setting

we have $\gamma_{\varepsilon}\in\Gamma_{b}$ with, by (4.10) in Lemma 4.2,

By (4.11) we have

and so

Since $\|\nabla u_{\varepsilon}\|_{2} = \varepsilon^{\tfrac{N-2}2}\|\nabla u\|_{2}$, $\|u_{\varepsilon}\|_{2} = \varepsilon^{\tfrac N2}\| u\|_{2}$, $\| u_{\varepsilon}\|_{p+1} = \varepsilon^{\tfrac N{p+1}}\| u\|_{p+1}$ for $\varepsilon\in(0, 1)$ we obtain

As in (4.15) we have furthermore that

Hence, by (4.21) we obtain that for all $u\in X\setminus\{0\}$ there exists a constant $C > 0$ such that for $\varepsilon\in(0, 1)$ we get

Since $N > 1$ and $p+1 > 2^{*}_{N+1}$ we have

and (4.22) gives

We now consider the case $p+1\leq 2^{*}_{N+1}$ and prove that $d_{J}({{\cal V}}_{-}^{b}, {{\cal V}}^{b}_{+}) > 0$ for any $b\in [0, c)$. We first observe that, for $u_{0}$ as given in Theorem 4.1, we have

Indeed, for $b\in [0, c)$ let $\alpha_{u_0, b}$ and $\omega_{u_0, b}$ be given by Remark 4.1 and define

Then $\gamma\in \Gamma_{b}$ and, since $t_{u_{0}} = 1$, (4.11) gives $\|\dot \gamma(t)\|_{2} = (\omega_{u_0, b}-\alpha_{u_0, b})\|u_{0}\|_{2}\leq \tfrac{p+1}2\|u_{0}\|_{2}$. Hence, since $V(\gamma(t))\leq V(u_{0}) = c$ for any $t\in [0, 1]$, (4.23) follows.

Let now $(\gamma_{n})\subset {{\Gamma}}_{b}$ be such that

By Remark 4.3 and by continuity, for $n\in{{\bf N}}$, there is $s_{n}\in (0, 1)$ such that $\gamma_{n}(s_{n})\in{\cal N}$ and $V'(\gamma_{n}(t))\gamma_{n}(t) > 0$ for any $t\in [0, s_{n})$.

We analyse first the case in which $\gamma_{n}(s_{n})$ is not bounded in $X$ assuming that along a subsequence, still denoted $(\gamma_{n}(s_{n}))$, we have

By (4.24) we have in particular

By (4.16) we know that $\|\gamma_{n}(s_{n})\|_{2}\geq (\tfrac 1{K_{G}})^{\frac {1}{\theta_{N, p}}}\frac 1{\|\nabla \gamma_{n}(s_{n})\|_{2}^{\sigma_{N, p}}}$ and by Lemma 4.6, if $t\in [0, s_{n})$ is such that $\|\gamma_{n}(t)-\gamma_{n}(s_{n})\|_{2}\leq (\tfrac 1{4K_{G}})^{\frac {1}{\theta_{N, p}}}\frac 1{\|\gamma_{n}(s_{n})\|^{\sigma_{N, p}}}$ then

By (4.25) there exists $\bar n\in{{\bf N}}$ such that $(\tfrac 12)^{p+1}V(\gamma_{n}(s_{n})) > b\ge V(\gamma_{n}(0))$ for any $n\geq\bar n$ and so $\|\gamma_n(0)-\gamma_n(s_n)\| > \left(\tfrac 1{4K_{G}}\right)^{\frac {1}{\theta_{N, p}}}\frac1{\|\gamma_{n}(s_{n})\|^{\sigma_{N, p}}}$. Then, for any $n\geq \bar n$ there is $\bar s_{n}\in (0, s_{n})$ such that

$(i)$ $\|\gamma_{n}(t)-\gamma_{n}(s_{n})\|_{2}\leq (\tfrac 1{4K_{G}})^{\frac {1}{\theta_{N, p}}}\frac 1{\|\gamma_{n}(s_{n})\|^{\sigma_{N, p}}}$ for any $t\in (\bar s_{n}, s_{n})$,

$(ii)$ $\|\gamma_{n}(\bar s_{n})-\gamma_{n}(s_{n})\|_{2} = (\tfrac 1{4K_{G}})^{\frac {1}{\theta_{N, p}}}\frac 1{\|\gamma_{n}(s_{n})\|^{\sigma_{N, p}}}$,

$(iii)$ $V(\gamma_{n}(t))\geq (\tfrac 12)^{p+1}V(\gamma_{n}(s_{n}))$ for any $t\in (\bar s_{n}, s_{n})$.

Since $V(\gamma_{n}(s_{n}))\to+\infty$, by $(iii)$ we can assume that for $n\geq\bar n$ we have $V(\gamma_{n}(t))-b\geq (\tfrac 12)^{p+2}V(\gamma_{n}(s_{n}))$ for any $t\in (\bar s_{n}, s_{n})$. Hence, using $(i)$ and $(ii)$ we obtain

If $p+1 < 2^{*}_{N+1}$ by (4.17) we have $\sigma_{N, p} < 1$ and so the above inequality would imply

in contradiction with (4.23). So the case (4.24) cannot occur when $p+1 < 2^{*}_{N+1}$. If $p+1 = 2^{*}_{N+1}$ by (4.17) we have $\sigma_{N, p} = 1$ and the above inequality gives

Since $d_{J}({{\cal V}}_{-}^{b}, {{\cal V}}^{b}_{+}) = \lim_{n\to+\infty}\int_{0}^{1}\|\dot \gamma_{n}(t)\|_{2}\sqrt{2(V(\gamma_{n}(t))-b)}\, dt$, this proves that the Jacobi distance between ${{\cal V}}^{b}_{-}$ and ${{\cal V}}^{b}_{+}$ is positive in this case.

To conclude the proof of the Proposition we have finally to consider the case in which $(\gamma_{n}(s_{n}))$ is bounded in $X$. We claim that in this case for any $\beta\in [0, c)$ there exists $d_\beta > 0$ such that

Indeed, by Remark 4.4, ${{\cal V}}_{-}^{\beta}$ is weakly compact in $X$. Then for any $n\in{{\bf N}}$ there exists $v_{n}\in {{\cal V}}_{-}^{\beta}$ such that ${{\mathrm{dist}}}_{L^{2}(\mathbb{R}^{N})}(\gamma_{n}(s_{n}), {{\cal V}}_{-}^{\beta})\geq\|\gamma_{n}(s_{n})-v_{n}\|_{L^{2}(\mathbb{R}^{N})} > 0$ and (4.26) will follows if we show that $\liminf_{n\to+\infty}\|\gamma_{n}(s_{n})-v_{n}\|_{L^{2}(\mathbb{R}^{N})} > 0$. To this aim assume by contradiction that $\liminf_{n\to+\infty}\|\gamma_{n}(s_{n})-v_{n}\|_{L^{2}(\mathbb{R}^{N})} = 0$. By the weak compactness of ${{\cal V}}_{-}^{\beta}$ and the boundedness of $(\gamma_{n}(t_{n}))$, there exist $v_{0}\in {{\cal V}}_{-}^{\beta}$ and $u_{0}\in X$ such that, along common subsequences still denoted $(\gamma_{n}(s_{n}))$ and $(v_{n})$, we have $\|\gamma_{n}(s_{n})-v_{n}\|_{2}\to 0$, $v_{n}\to v_{0}$ and $\gamma_{n}(s_{n})\to u_{0}$ weakly in $X$ and strongly in $L^{p+1}(\mathbb{R}^{N})$. Since $\|\gamma_{n}(s_{n})-v_{n}\|_{2}\to0$, by weak semicontinuity of the norm we recover $\|u_{0}-v_{0}\|_{L^{2}(\mathbb{R}^{N})} = 0$. Hence $u_{0} = v_{0}\in {{\cal V}}^{b}_{-}$. Since $V(\gamma_{n}(s_{n}))\geq c > b$ and $V(u_{0})\leq b$ we then have that $\gamma_{n}(s_{n})$ does not converge strongly in $X$ to $u_{0}$ and so $\|u_{0}\| < \liminf_{n\to+\infty}\|\gamma_{n}(s_{n})\|$. In particular, since by the strong convergence in $L^{p+1}(\mathbb{R}^{N})$ we have $\|\gamma_{n}(s_{n})\|_{p+1}^{p+1}\to \|u_{0}\|_{p+1}^{p+1}$, we obtain

which says that $V'(u_{0})u_{0} < 0$ in contradiction with $u_{0}\in {{\cal V}}^{b}_{-}$, by (4.13). Then (4.26) follows.

In particular (4.26) gives that for $\beta = \tfrac 12 (b+c)$ there exists $d_{\beta} > 0$ such that

Since $V(\gamma_{n}(0)) = b$ and $V(\gamma_{n}(s_{n}))\geq c$, by (4.27) and by continuity there exists $\bar s_{n}\in (0, s_{n})$ such that

(iv) $V(\gamma_{n}(t))\geq \tfrac 12(b+c)$ for any $t\in (\bar s_{n}, s_{n})$, (v) $\|\gamma_{n}(\bar s_{n})-\gamma_{n}(s_{n})\|_{2}\geq d_{\beta}$.

Using $(iv)$ and $(v)$, we derive

and the proposition is proved.

Conflict of interest

The authors declare they do not have a conflict of interest.