We consider a Landau-de Gennes model for a polydisperse, inhomogeneous suspension of colloidal inclusions in a nematic host, in the dilute regime. We study the homogenised limit and compute the effective free energy of the composite material. By suitably choosing the shape of the inclusions and imposing a quadratic, Rapini-Papoular type surface anchoring energy density, we obtain an effective free energy functional with an additional linear term, which may be interpreted as an "effective field" induced by the inclusions. Moreover, we compute the effective free energy in a regime of "very strong anchoring", that is, when the surface energy effects dominate over the volume free energy.
1.
Introduction
Topological data analysis (TDA) is a scientific field lying at the crossroads of applied topology and data analysis: objects like functions and point clouds are typically studied by means of possibly multidimensional complexes of homology groups [29] obtained with different pipelines. Homology groups considered with coefficients in a field K are vector spaces, whose dimension is determined by different kinds of "holes" which can be found in a space and, thus, provide a rich characterization of the shape of the space the analyst is considering. More precisely, each statistical unit induces a whole family of topological spaces indexed on Rn, which then, via homology, produces a family of vector spaces indexed on the same set more precisely, a functor [35] (Rn,≤)→VectK. Such collections of vector spaces are called persistence modules [14], with multidimensional persistence modules being a special reference to the cases in which n>1, and describe the shape of the data by considering interpretable topological information at different resolutions. A topological signature/summary or an invariant of a persistence module is a representation which usually maps persistence modules into a metric space or even a vector space so that some kind of analysis can be carried out. The most used topological summaries for 1-D persistence (i.e., n=1) include persistence diagrams [21], persistence landscapes [12], persistence images [2], and persistence silhouettes [15]. When dealing with 0-dimensional homology and 1-D persistence, if the space X is path connected, another topological summary called merge tree [9] can be employed. A merge tree is a tree-shaped topological summary which captures the evolution of the path connected components π0(Xt) of a filtration of topological spaces {Xt}t∈R, with Xt↪Xt′ if t≤t′.
One of the central ideas in TDA is the one of stability properties, i.e., the properties related to the continuity of the operator mapping data into topological signatures. One definition which has gained a lot of success is the one of ε-interleavings between topological representations: when adding some kind of ε-noise to the data, the associated summary "moves" by at most ε. If this happens, then the operator mapping functions to topological representations is a non-expansive Lipschitz operator. Starting from the bottleneck distance for persistence diagrams [22], this idea has been applied to 1-D persistence modules [14], multidimensional persistence modules [34], merge trees [9], sheaves [17,38], and more general situations [10,19]. In this paper, we focus on the problem of studying interleavings for merge trees.
The main reason to pursue such research direction is that merge trees and persistence diagrams are not equivalent as topological summaries, that is, they do not represent the same information with merge trees being able to distinguish between scenarios which persistence diagrams and all the other equivalent summaries cannot [16,23,33,47]. As a consequence, in recent years, a lot of research sparked on merge trees, mainly driven by the need of having a stable metric structure to compare such objects. Stable and unstable edit distances between Reeb graphs or merge trees have been proposed by [7,20,41,48], while other works focus on (unstable) Wasserstein distances [43], lp distances [13] and interleaving distances between merge trees [3,9,11,25,28] or Reeb graphs [8,17,18,38].
1.1. Related works
The problem of computing the interleaving distance between merge trees has already been approached by [3] and [25] in an attempt to approximate the Gromov-Hausdorff (GH) distance when both metric spaces are metric trees. In this situation, in fact, up to carefully choosing the root of the metric trees, the two metrics are equivalent. Both problems approximating the GH distance and computing the interleaving distance have been shown to be NP-hard [3,11], and, thus, even obtaining feasible approximation algorithms for small trees is a daunting task.
In [3], the authors provide a polynomial time algorithm to approximate the interleaving distance between merge trees via binary search. They build a set which contains the solution of the optimization problem and then obtain a criterion to assess if certain values of the aforementioned set can be excluded from the set of solutions. If the length of the branches of both trees is big enough, one can carry out the binary search over all possible couples of vertices, with one vertex from the first tree and one from the second. If trees have branches that are too small, the decision procedure is coupled with a trimming step to deal with these smaller edges. The algorithm returns an approximation of the interleaving distance, with the approximation factor depending on the ratio between the longest and the shortest edge in the tree and the number of vertices.
The authors of [25], instead, propose the first algorithm for the exact computation of the interleaving distance. Starting from a novel definition of the interleaving distance, they develop a faster alternative to exclude values from the same set of solutions considered by [3]. By filtering a finite subset of points on the metric trees (in general, bigger than the set of vertices of the "combinatorial" trees) according to a) their heights and b) a candidate optimal value δ, in an up-bottom fashion, points of the second tree are matched to subsets of points of the first tree. Such matching means that all points of the first tree inside in the chosen collection can be potentially mapped in the point of the second tree via some function viable for the interleaving distance. Each such matching (S,w) is then used to establish similar couples (set, point) between the children of the points involved: the set of points of the first tree is to be chosen among the compatible subsets of the children of S, and the point in the second tree among the children of w. If no such couples are found, δ is discarded. The algorithm they propose to compute the interleaving distance has complexity O(n2log3(n)22τττ+2), where n is the sum of the vertices in the two merge trees, and τ is a parameter depending on the input trees, which is defined by the authors. The key issue is that τ can be very big also for small-sized trees: In [25], in Figure 2, the authors showcase a tree with 8 leaves and τ=13 (thus, the complexity of the algorithm is at least O(n2log3(n)2261315)∼O(n2log3(n)1024).
Due to its computational complexity, the algorithm by [25] has not been implemented by other authors working with merge trees [16], which instead have exploited another formulation of the same metric, provided by [28]. This last formulation relies on a definition of the interleaving distance between merge trees which are endowed with a fixed set of labels on their vertices. The usual interleaving distance is then shown to be equivalent to choosing an appropriate set of labels potentially upon adding some vertices to the trees for the two given merge trees. This formulation, per se, does not provide computational advantages over the classical one, since evaluating all the possible labelings of a tree would still be unfeasible. However, [16] proposes a labeling strategy which should provide "good" labels. Despite being computationally accessible even for very big trees, this approach has the downside of not providing methods for assessing the error of the produced estimate.
1.2. Contributions
In this work, we pursue two main objectives. First, we aim to establish the theoretical foundations necessary to derive reliable polynomial upper and lower bounds for the interleaving distance. Second, we seek to develop practical techniques that complement those proposed in [3] and [25]. As demonstrated in Appendix B, our methods offer computational procedures that are more efficient than those in [25] and more reliable than those in [3].
To do so, we take a perspective which differs from all the aforementioned works: instead of obtaining progressively sharper bounds for the distance by locally looking at differences between trees or instead of looking for optimal labelings, we aim at describing jointly a global matching between two merge trees whose cost returns the exact interleaving distance between them. In this way, we obtain a novel combinatoric formulation of the interleaving distance between merge trees, which we also conjecture to be equivalent to yet another formulation, supported by the already established link between the interleaving and the GH distances between trees [25].
Expressing distances between trees by matching their vertices is a very common approach for edit distances. Notably, there are very strong relationships between the couplings we use in this paper and the mappings which appear ubiquitously in edit distance literature. This allows us to leverage ideas and techniques developed in such research areas, advancing the theoretic and computational tools at our disposal. In particular, as summarized by Figure 14, in Appendix A, we specifically adopt two key ideas from edit distance frameworks:
1) Defining constrained variations of computationally expensive metrics, which maintain strong practical performance while improving computational efficiency. Most works on edit distances for merge trees [48,49,52,53] follow this exact path: they define "unconstrained" distances whose computational cost is NP-Hard [30], and then exploit the polynomial algorithms in [32,46,54] to obtain some "constrained" upper bounds, which can also be regarded as a metric on their own;
2) Developing recursive methods for computing both constrained and unconstrained formulations of distances, thereby reducing the computational burden and enabling recursive mixed/integer linear programming approaches, as in [31,41,52].
We exploit our novel formulation precisely to produce 1) a constrained version of the interleaving distance and 2) a recursive procedure to obtain upper and lower bounds for such distance via mixed linear programming. As previously stated, the bounds we derive in this way complement the procedures in [3] and [25], thereby extending the applicability of the interleaving distance, as discussed in Appendix B. It is important to note, however, that this comparison is rather technical and considers some particular scenarios, due to the profound different natures of the considered algorithms.
Given that our recursive procedure returns bounds whose computational costs are very close to the ones of [48,49,52,53], we believe that studying the combination of the recursive procedure on the constrained interleaving distance may similarly lead to polynomial-time bounds for the interleaving distance mirroring what has been achieved for the edit distances in the cited works. See Proposition 6 and Section 9.2.9.
In the last part of the paper, we test those bounds by comparing them with the method proposed by [16] to estimate the interleaving distance and by tackling a number of simulated and real-data case studies, showcasing also how to empirically assess the validity of our estimates.
1.3. Outline
The paper is organized as follows: In Section 2, we introduce merge trees first in a combinatorial fashion and then as "continuous" posets and metric spaces, recalling the definition of interleaving distance. In Section 3, we introduce a partial matching between trees called coupling. Relationships between these matchings and maps between trees are then presented in Section 4. Section 5 and Section 6 prove the equivalence between the usual definition of interleaving distance and the problem of finding optimal couplings.
In the second part of the manuscript, we leverage our novel formulation to introduce a constrained variant of the interleaving distance in Section 7, followed by the development of decomposition procedures for the interleaving distance in Section 8. We then present estimation methods for the interleaving distance in Section 9, and evaluate their performance through experiments described in Section 10. Finally, Section 11 concludes the main body of the paper with a brief discussion of our findings.
Appendix A contains two flowcharts, which can help the reader navigating the structure of the manuscript and Table 3, which collects most of the main pieces of notation introduced in the manuscript, and can help the reader navigating the most technical sections. Appendix B features a comparison of our algorithms with the ones of [3] and [25]. Appendix C presents a further simulation dealing with the computational runtimes of the current implementation of our methods. Appendix D contains some of the proofs of the results in the manuscript, while the other ones are reported right after the statement they relate to, as they can help the reader in following the discussion.
2.
Merge trees and interleaving distance
We start by introducing merge trees as combinatorial objects along with their "continuous" counterpart.
2.1. Merge trees as finite graphs
In accordance with other authors, we call a merge tree a rooted tree with a suitable height function defined on its vertices. We now state the formal definition, introducing some pieces of notation which we will use to work with those objects throughout the paper.
Definition 1. A tree structure T is given by a set of vertices VT and a set of edges ET⊂VT×VT, which form a connected rooted acyclic graph. We indicate the root of the tree with rT. We say that T is finite if VT is finite. The degree of a vertex v∈VT is the number of edges which have that vertex as one of the extremes. Any vertex with an edge connecting it to the root is its child, and the root is its father: this is the first step of a recursion which defines father and children relationships for all vertices in VT. Vertices with no children are called leaves or taxa and are collected in the set LT. The relationship child<father generates a partial order on VT. The edges in ET are represented by ordered couples (a,b) with a<b. A subtree of a vertex v, called subT(v), is the tree structure whose set of vertices is {x∈VT∣x≤v}.
In Definition 1, we introduce the term tree structure to differentiate such objects from the generic word "tree", which we will use to indicate either a tree structure, a merge tree, or a metric tree, when the context allows to lighten the notation.
Given finite sets A,B, we indicate with #A the cardinality of one set and with A−B:={a∈A∣a∉B}. Moreover, given a finite poset P, we indicate with maxP the set of all its maxima, and minP the set of all its minima. Given A⊂VT and v∈VT, we may also write maxv′<vA to indicate the maximal elements in the set {v′∈A∣v′<v} according to the poset structure inherited from VT.
Identifying an edge (v,v′) with its lower vertex v gives a bijection between VT−{rT} and ET, that is, ET≃VT−{rT} as sets. Given this bijection, we may use ET to indicate the vertices v∈VT−{rT} to simplify the notation.
Now, we give the notion of least common ancestor between vertices.
Definition 2. Given a set of vertices A={a1,…,an}⊂VT, we define LCA(a1,…,an)=min⋂ni=1{v∈VT∣v≥ai}.
Now, to obtain a merge tree, we add an increasing height function to a tree structure.
Definition 3. A merge tree (T,f) is a finite tree structure T such that the root is of degree >1, coupled with a monotone increasing function f:VT→R.
Remark 1. Definition 3 is slightly different from the definition of merge trees found in [28], [40], and other works. In particular, in the present work, we do not need to have a root at infinity and thus, for us, the root is the highest vertex with finite height. Similarly, the function coupled with the tree structure in literature is usually referred to as hT being a "height" function. To avoid ovearloading the notation, since we need to introduce many subscripts and superscripts, we call these functions with more usual functional notations like f or g.
Assumption 1. To avoid formal complications, we make the following standard genericity assumption for any merge tree (T,f):
(G) f:VT→R is injective.
Example 1. Given a real valued Morse [37] function f:X→R defined on a path connected compact space X, the sublevel set filtration is given by Xt=f−1((−∞,t]), together with the maps Xt<t′=i:f−1((−∞,t])↪f−1((−∞,t′]). We can describe the family of sets and maps {π0(Xt)}t∈R via a merge tree. See, for instance, [16,40]. Similarly, we can consider a finite set C⊂Rn and take its Céch filtration: Xt=⋃c∈CBt(c), with Bt(c)={x∈Rn∣∥c−x∥<t}. As before: Xt<t′=i:⋃c∈CBt(c)↪⋃c∈CBt′(c) and {π0(Xt)}t∈R can be represented via a merge tree.
Before proceeding, we need one last graph-related definition which we use to denote some particular kinds of paths on the tree structure of a merge tree.
Definition 4. Given a merge tree T, a sequence of edges is an ordered sequence of adjacent edges {e1,…,en}. This means that we have e1<…<en, according to the order induced by the bijection ET↔VT−{rT}, and that ei and ei+1 share a vertex. We will use the notation [v,v′] to indicate a sequence of edges which starts in the vertex v and ends before v′, with v<v′. Thus, the edge associated to v (via ET≃VT−{rT}) is included in the sequence, while the one associated to v′ is the first one excluded.
In the left column of Figure 1, the reader can find an example of a merge tree, which can be used to get familiar with the definitions just given. For instance, one can check that, using the notation of the figure, e=LCA(a,b,d) and [a,c,r] is an ordered sequence of edges, while [c,r,d] is not.
2.2. Metric merge trees
Now we consider the continuous version of a merge tree, intuitively obtained by considering all the points in the edges of a merge tree as points of the tree itself. For a visual intuition of the following ideas, the reader may refer to Figure 1.
Definition 5. Given a merge tree T, we obtain the associated metric merge tree as follows:
where, for every v∈VT, f(v)∼f(v′) if v=v′. We refer to the points in T with the same notation we use for vertices in vT: x∈T; with f(x), we indicate the height values of x.
For every point x∈VT, we can identify x with the point f(x)∈[f(x),f(x′)], with (x,x′)∈ET, or, equivalently, with f(x)∈[f(x′),f(x)], if (x′,x)∈ET. This induces a well-defined map VT↪T. Thus, given v∈VT, with an abuse of notation, we can consider v∈T. Note that the height function f:T→R extends the function defined on the vertices of the merge tree. Every point in T−VT belongs to one, and only one, interval of the form [f(x),f(x′)]. Thus, we can induce a partial order relationship on T by ordering points first with the partial order in ET and then with the increasing internal order of [f(x),f(x′)]. Thus, we can explicitly write down the shortest path metric in T: d(x,x′)=f(LCA(x,x′))−f(x)+f(LCA(x,x′))−f(x′).
Remark 2. (Notation and previous works) If we start from a morse function f:D→R defined on a compact and path connected topological space D, what we call "metric merge tree" is essentially the "merge tree" of f, according to the topological definition given in [9], also called classical merge tree in [16]. Moreover, display posets of persistent sets, as defined in [16], are up to some additional hypotheses equivalent to metric merge trees. However, 1) we are interested at working on merge trees in a combinatorial fashion, so we build merge trees as graphs and then bridge to this continuous construction; and 2) in order to use display posets, we would need to give other technical definitions, which we do not need in this work; thus, we avoid working with such objects. To sum up, all these procedures/definitions are different ways to build an R-space (X,fX:X→R) with fX continuous function [18] with the underlying topological space X being the CW-complex associated to a tree. In particular, the display poset highlights the poset structure of such topological space while the approach in [9] describes a geometric construction, which gives the display poset a natural topology.
For each metric tree T, we have a family of continuous maps, skT:T→T, with k≥0, called structural maps, defined as follows: skT(x)=x′ with x′ being the only point in T such that x′≥x and f(x′)=f(x)+k.
2.3. Interleaving distance between merge trees
Now, we recall the main facts about the interleaving distance between merge trees, relying on [9].
Definition 6. [9] Two continuous maps α:T→G and β:G→T between two metric merge trees, (T,f) and (G,g), are ε-compatible, with ε≥0, if the following hold:
(I1) g(α(x))=f(x)+ε for all x∈T and f(β(y))=g(y)+ε for all y∈G;
(I2) αβ=s2εG and βα=s2εT.
The interleaving distance between T and G is then:
For an example of continuous maps α and β satisfying (I1), see Figure 2. Such maps also satisfy (I2), as shown by Figure 3.
The work of [25] shows that the existence of α and β is in fact equivalent to the existence of a single map α with some additional properties, which are stated in the next definition.
Definition 7. [25] Given two metric merge trees (T,f) and (G,g), an ε-good map α:T→G is a continuous map such that:
(P1) g(α(x))=f(x)+ε for all x∈T;
(P2) if α(x)<α(x′), then s2εT(x)<s2εT(x′);
(P3) if y∈G−α(T), then, given w=min{y′>y∣y′∈α(T)}, we have g(w)−g(y)≤2ε.
As anticipated, [25] proves that two merge trees are ε-interleaved if, and only if, there is an ε-good map between them.
3.
Couplings
Now, we start our combinatorial investigation. Across the following sections, we need to introduce several pieces of notation, which are also summarized in Table 3 in the appendix.
Given two merge trees T and G, we would like to match their vertices and compute the interleaving distance relying only on such matches. To match the two graphs, we will use a set C⊂VT×VG, which will tell us which vertex is coupled with which. For such C, we call πT:C→VT the restriction of the projection of the cartesian product. Since VT and VG are posets, we can introduce a partial order relationship on any C⊂VT×VG, having (a,b)<(c,d), if and only if, a<c and b<d. Thus, as for each of the sets VT, VG, and any subset of those sets, we can consider the set of the maximal elements and the set of the minimal elements of C (and its subsets), which we indicate with maxC,minC, etc.
Clearly, a coupling C must satisfy some constraints, which we now introduce.
We start by defining the "multivalued" function ΛTC:VT→P(VT), with P(VT) being the power set of VT.
Definition 8. A coupling between two merge trees (T,f) and (G,g) is a set C⊂VT×VG such that:
(C1) #maxC=1;
(C2) the projection πT:C→VT is injective (the same for G);
(C3) given (a,b) and (c,d) in C, then a<c if, and only if, b<d;
(C4) a∈πT(C) implies #ΛTC(a)≠1 (the same for G).
The set of couplings between T and G is called C(T,G). Note that, thanks to (C3), (C1) can be replaced by #maxπT(C)=#maxπG(C)=1.
We invite the reader to follow the remaining of the section looking at Figure 4, which can help in understanding the comments we present on properties (C1)–(C4) and visualizing the pieces of notation we need to establish.
We collect the set of points v∈ET such that #ΛTC(v)=1 in a set, which we call UTC. Instead, the points such that v∉πT(C) and #ΛTC(v)≠1 are collected in a set DTC. Note that the sets πT(C),UTC and DTC are a partition of VT.
A couple (v,w)∈C means that we match a vertex v∈VT with a vertex w∈VG. It is clear from the definition that there can be vertices left out from this matching. We regard these vertices as unnecessary for the coupling C: when we will induce maps between metric merge trees starting from couplings, the position of these vertices inside the metric merge tree G will be completely induced by other vertices in VT. Among the vertices not appearing in the couples of C, we distinguish between two situations: having a vertex v in DTC, informally, means that the edge (v,father(v)) except in certain special cases is not contained in the image of β(α(T)), with α and β as in Definition 6. For this reason, we say that the vertices in DTC and DGC are deleted by the coupling C. Instead, the vertices v∈UTC are vertices which are unused, ignored by the coupling, and will be of no importance in the computation of the distance.
In this context, property (C1) is asking that there is a unique maximal couple in C, while (C2) is asking that each vertex is paired with at most one other vertex of the other merge tree. Note the maps α:T→G in Definition 6 are not forced to be injective, but, as we will prove in later sections, for our purposes it is enough to couple points just one time. Condition (C3) is asking that the coupling respects the tree structures of T and G; in particular, this implies that (maxπT(C),maxπG(C))∈C. Lastly, due to condition (C4), we avoid coupling vertices which have only one coupled element below them.
Given a coupling, we want to associate to a vertex a cost which indicates how much the coupling moves that vertex. In order to do so, we define the following functions:
● Define φTC:VT→VT so that φTC(x)=min{v∈VT∣v>x and #Λ(v)≠0}. Note that since the set {v∈VT∣v>x} is totally ordered, φTC(x) is well-defined;
● Similarly, define δTC:VT→VT, defined as δTC(x)=min{v∈VT∣v≥x and v∈πT(C)};
● Define χTC:VT→VG, defined as χTC(x)=LCA({πG((v,w))∣v∈ΛT(x)});
● Set γTC:VT−DTC→VG to be:
Note that if #{g(w)∣(v,w)∈C,v<x}>0, by (G), γTC(x) is uniquely defined, and so γTC is not a multivalued function. Moreover, γTC(φTC(x)) is well-defined for any v∈VT.
Remark 3. When clear from the context, to lighten the notation, we might omit the subscripts and superscripts. For instance, if we fix C∈C(T,G) and x∈VT, we refer to γTC(φTC(x)) as γ(φ(x)). Similarly, we use x∈U, x∈D, respectively, for x∈UTC and x∈DTC.
Given x∈VT, in what follows we will encounter the following objects (see Figure 4),
● η(x):=γ(φ(x)) is the vertex in VG obtained in this way: starting from x, we go toward rT until we meet the first point of VT which has at least one vertex in its subtree which is not deleted; we consider the subtree of such a vertex and take all the vertices of VG which are coupled with elements in this subtree (such a set is not empty); lastly, we take the vertex with the lowest height among this set;
● Given x such that x∈D and #Λ(x)>1, we often consider δ(x); note that for every v such that x≤v<δ(x), then v∈D and #Λ(v)>1. Thus, [x,δ(x)] contains only deleted vertices;
● Similarly, for x such that x∈D and #Λ(x)>1, we take χ(x): that is, the lowest point in G, where x can be sent compatibly with C and the tree structures of T and G. Thus, if (x,y)∈C, y≥χ(x).
Remark 4. As anticipated in the introduction, the definition of couplings has strong connections with the definition of mappings given in [41] and which is used to compute the edit distance therein defined. Such definition generalizes more classical definitions of mappings, which are ubiquitous in the literature of edit distances for trees. In particular, one can show that given a coupling C∈C(T,G), if we add to C:
● Couples of the form (a,D) for every a∈VT such that a is deleted, i.e., a∉πT(C) and #ΛTC(a)≠1;
● Couples of the form (D,b) for every b∈VG such that b is deleted, i.e., b∉πG(C) and #ΛGC(b)≠1;
● Couples of the form (a,G) for every a∈VT such that a is unused, i.e., a∉πT(C) and #ΛTC(a)=1;
● Couples of the form (G,b) for every b∈VG such that b is unused, i.e., b∉πG(C) and #ΛGC(b)=1.
We obtain a set MC, which is a mapping in the sense of [41].
4.
Couplings, maps, and costs
We now start introducing our novel formulation of the interleaving distance. We do so in a 3 step procedure which is summarized in Figure 14(a) in the appendix.
In this section, we establish some correspondence between couplings and maps α:T→G, giving also the definition of the cost of a coupling. As a first step, given a coupling C, we induce two maps αC:VT−UTC→G and βC:VG−UGC→T, following these rules:
1) If (x,y)∈C, then αC(x):=y.
2) x∈DTC with #Λ(x)=0, then αC(x):=skT(η(x)) with k being:
● k=f(x)+12(f(φ(x))−f(x))−g(η(x)) if g(η(x))≤f(x)+12(f(φ(x))−f(x));
● k=0, otherwise.
Where the idea is that we want to send x above some coupled vertex changing its height "as little as possible". Bear in mind that the sequence [x,φ(x)] should not appear in the image of βα.
3) If instead x∈DTC with #Λ(x)>1, then αC(x):=χ(x).
The map βC is obtained in the same way, exchanging the roles of (T,f) and (G,g). Figure 5(b) shows an example in which βC is obtained starting from a coupling.
As a first result, we obtain that the maps we induce respect the tree structures of the respective merge trees.
Proposition 1. Consider x,x′∈VT−UT: if x<x′, then αC(x)≤αC(x′).
Now, we need to extend αC to a continuous function between T and G. To formally extend the map, we need the following lemma.
Lemma 1. Any x∈T such that x∉πT(C)∪D, is contained in a sequence of edges [lC(x),uC(x)] such that lC(x)∈max{v≤x∣v∈πT(C)∪D}, and uC(x) is either uC(x)=+∞ or uC(x)=min{v≥x∣v∈πT(C)∪D}. Moreover, lC(x) is unique if {v∈U∣lC(x)≤v≤x}=∅, meanwhile, if {v∈U∣lC(x)≤v≤x}≠∅, there exists a unique lC(x) such that lC(x)∉D.
Now, we can obtain a continuous map αC:T→G.
Proposition 2. We can extend αC to a continuous map between T and G. This map, with an abuse of notation, is still called αC.
Proof. We define αC(x) for x∉πT(C)∪DTC. By Lemma 1, we have x∈[l(x),u(x)], with αC being defined for l(x) and u(x). Whenever l(x) is not unique, we take the unique l(x)∈πT(C). Clearly, we have f(l(x))<f(x)<f(u(x)). Thus, if u(x)<+∞, there is a unique λ∈[0,1] such that f(x)=λf(l(x))+(1−λ)f(u(x)). Having fixed such λ, we define αC(x) to be the unique point in [αC(l(x)),αC(u(x))], which is a sequence of edges thanks to Proposition 1 with height λg(αC(l(x)))+(1−λ)g(αC(u(x))). If u(x)=+∞, then x>v with v=maxπT(C). Then, we set αC(x)=y such that y≥αC(v) and g(y)=g(αC(v))+f(x)−f(v). Note that, for x,x′ such that u(x),u(x′)=+∞, the map αC always preserves distances, and we have g(αC(x))−f(x)=g(αC(v))−f(v). Thus, at such points it is a continuous function.
Consider now a converging sequence xn→x in T. We know that definitively {xn}n∈N is contained in one or more edges containing x. Thus, we can obtain a finite set of converging subsequences by intersecting {xn} with such edges. With an abuse of notation, from now on, we use {xn}n∈N to indicate any such sequence. Each of those edges is contained in a unique sequence of edges of the form [l(x′),u(x′)], for some x′ (up to, eventually, taking l(x′)∉D). Thus, {xn}⊂[l(x′),u(x′)] induces a unique sequence {λn}⊂[0,1] such that f(xn)=λnf(l(x′))+(1−λn)f(u(x′)) and λn→λx, with f(x)=λxf(l(x′))+(1−λx)f(u(x′)). By Lemma 1, αC(x)∈[αC(l(x′)),αC(u(x′))]. Moreover, by construction, g(αC(xn))→λxg(αC(l(x′)))+(1−λx)g(αC(u(x′)))=g(αC(x)). Thus, αC is continuous.
□
In order to start relating maps induced by couplings and ε-good maps, we define the cost of the coupling C, which is given in terms of how much the (continuous) αC:T→G moves the points of T. To highlight the domains of the maps involved in the following definition, we make use of the identity map IdT:T→T, for a metric tree T.
Definition 9. Given C∈C(T,G) and x∈T, we define costC(x)=∣g(αC(x))−f(x)∣. Coherently, we define ∥C∥∞=max{∥g∘αC−f∘IdT∥∞,∥f∘βC−g∘IdG∥∞}.
Note that, given C∈C(T,G) and x∈T, we have one of the following possibilities:
● If (x,y)∈C, costC(x)=∣f(x)−g(y)∣;
● If x∉πT(C)∪D, costC(x)≤max{costC(l(x)),costC(u(x))}; in fact,
● We are left with the case x∈D. We have two different scenarios:
a) If #Λ(x)=0, then costC(x)=max{(f(φ(x))−f(x))/2,g(η(x))−f(x)}. We point out that (f(φ(x))−f(x))/2 is the cost of deleting the path [x,φ(x)] in two steps: when applying α we halve the distance between x and φ(x), and then with β we obtain f(βα(x))=f(φ(x)). This can happen if below w (with (δ(x),w)∈C) there is "room" to send x at height f(x)+(f(φ(x))−f(x))/2; if, instead, η(x) is higher than f(x)+(f(φ(x))−f(x))/2, we simply send x to η(x);
b) If #Λ(x)>1, we have costC(x)=∣f(x)−g(χ(x))∣.
As a consequence, we point out two facts:
1) For every α:T→G such that, for every x∈πT(C)∪D, α(x)=αC(x), we have:
2) If we fix some total ordering of the elements in VT∐VG, so that we can write VT∐VT′=(a1,…,an), then ∥C∥∞=max(cost(a1),…,cost(an)).
5.
From couplings to ε-good maps
In this section, we prove the first fundamental interaction between couplings and the interleaving distance between merge trees, with our final goal being to replace the problem of finding optimal maps with the combinatorial problem of obtaining optimal couplings. Figure 5 summarizes all the steps of the procedure, which is formally addressed in this section. Throughout the section, we fix a coupling C and some ε≥∥C∥∞.
We build a map αεC:T→G, defined as αεC(x)=skxG(αC(x)) with kx=f(x)+ε−g(αC(x)) depending on x. Note that, since g(αC(x))−f(x)≤ϵ for every x∈T, we always have kx≥0. Moreover, by construction, g(αεC(x))=g(αC(x))+f(x)+ε−g(αC(x))=f(x)+ε.
We want to prove that αεC is an ε-good map.
Remark 5. The map αεC is such that, given x,x′∈T with x<x′, we have αεC(x)<αεC(x′).
As a first step, we obtain that αεC satisfies some necessary conditions in order to be ε-good, it is in fact continuous, and moves points "upward" by ε.
Proposition 3. The map αεC is a continuous map between T and G such that for every x∈T, we have g(αεC(x))=f(x)+ε.
Before proving the main result of this section, we need a short lemma.
Lemma 2. Consider (v,w),(v′,w′)∈C, and take x=LCA(v,v′), y=LCA(w,w′). Then, ∣f(x)−g(y)∣≤ε.
At this point, we are ready to prove the remaining properties which make αεC an ε-good map.
Theorem 1. The map αεC defined in previous lines is an ε-good map.
6.
From ε-good maps to couplings
This time, we start from an ε-good map α:T→G and our aim is to induce a C with ∥C∥∞≤ε.
Given a metric merge tree T, we define the following map: ℓT:T→VT given by ℓT(x)=max{v∈VT∣v≤x}. Note that, if x∈VT, then ℓT(x)=x; otherwise, x is an internal vertex of one edge (a,b) (possibly with b=+∞) and ℓT(x)=a. With this notation, we introduce the following maps:
Note that we always have g(ϕ(v))≤g(α(v))≤f(v)+ε. These maps will be pivotal in the proof of the upcoming theorem, since they will help us in closing the gap between the continuous formulation of the interleaving distance and the discrete matching of merge trees via couplings. The reader should refer to Figure 6 for a visual example of the above definitions.
We prove a corollary which characterizes the maps we just defined.
Corollary 1. Let v,v′∈VT; if v<v′, then ϕ(v)≤ϕ(v′).
Clearly, an analogous result holds for ψ, which implies that, in the setting of the corollary, ψ(ϕ(v))≤ψ(ϕ(v′)).
Now, we prove the main result of this section.
Theorem 2. Given α ε-good map between T and G, there is a coupling C between T and G such that ∥C∥∞≤ε.
Putting together Theorems 1 and 2, we see that two merge trees are ε-interleaved if, and only if, there is a coupling C between the merge trees such that ∥C∥∞=ε. Thus, computing the interleaving distance amounts to finding a minimal-cost coupling between two merge trees. As a byproduct of this result, we obtain another proof that the interleaving distance between metric merge tree can be found as a minimum and not just as an infimum as in Definition 6, for the set of available couplings is finite.
We close this section with a conjecture which we want to investigate in future works, which stems from one of the definitions of the GH distance [1] and the already exploited link between such distance in the case of metric merge trees and the interleaving distance [25].
Given any map α:T→G, we define H(α):=maxx∈T∣g(α(x))−f(x)∣. Similarly, for any map μ:T→T, which thus rearranges the points of T, we set 2⋅D(μ)=maxx∈Td(x,μ(x)) (where d is the shortest path metric on T).
Conjecture 1. We conjecture that:
where α:T→G and β:G→T vary in the set of continuous monotone maps.
7.
Constrained interleaving distance
In this section, exploiting couplings, we define a variation of the interleaving distance, which we call constrained interleaving distance, following the literature on tree edit distances. In particular, we borrow the constrained condition for couplings from [54].
Definition 10. A coupling C is constrained if the following hold:
(CONS) for every a,b,c∈ET and a′,b′,c′∈ET′ such that (a,a′),(b,b′),(c,c′)∈C, we have:
Restricting the optimization domain to constrained mappings, we obtain the constrained interleaving distance.
Definition 11. We define the constrained interleaving distance between two merge trees T,T′ as:
As already mentioned, constrained definitions of mappings have been successfully employed to bring the computational cost of edit distances for merge trees into the realm of polynomial time algorithms [43,48,49,52,53]. Since our couplings are closely related to the mappings employed in [39,52] (see Remark 4), we intend to use this formulation as a pivotal building block to obtain practically accessible and reliable upper bounds also for the interleaving distance.
We point out that the definition of dcI depends heavily on the formulation of the interleaving distance via couplings, as condition (CONS) is much harder to characterize via the maps αC or αεC. For instance, even if C is a constrained coupling, we may have a vertex c with two children {a,b} such that b is coupled, a is deleted, and αC(a)≥αC(b). In this case, we would have:
The same scenario can be replicated also with αεC.
Due to the challenges and technicalities arising in characterizing the maps αC coming from a constrained coupling C, we leave a proper investigation of this constrained definition to future works. In particular, we conjecture that dCI is a metric between merge trees. Plus, together with the recursive procedure described in Section 8, we plan on using it to obtain a polynomial time algorithm viable for applications.
8.
Recursive decomposition properties
Now, we exploit the formulation of the interleaving distance via couplings to obtain recursive decomposition properties inspired by the ones of edit distance between trees. In particular, we prove that, under some conditions, optimal couplings can be computed via the solution of smaller independent subproblems, which are then aggregated to solve the global one. If the aforementioned conditions do not apply, we still obtain lower and upper bounds for the interleaving distance.
The main result of the section involves couplings with some strong properties, which we call special and collect under the following notation:
Before proceeding, we need a few pieces of notation used to lighten the dissertation and one last technical definition. Given x∈VT and y∈VG, we define Tx=subT(x) and Gy=subG(y). Moreover, CR(T,G):={C∈C(T,G)∣(rT,rG)∈C}. Similarly, we have CoR(T,G):=CR(T,G)∩Co(T,G).
Definition 12. Given a partially ordered set (A,<), A is an anti-chain if for any a,b∈A, a≠b, neither b>a or a>b hold. A subset of a poset is an anti-chain if it satisfies this condition with the restriction of the poset structure.
Now, we introduce the combinatorial objects we will use to decompose the following optimization problem: minC∈C(T,G)∥C∥∞. The reader may look at Figure 7 to find examples involving the following definition.
Definition 13. We define C∗(T,G) as the set of all C∗⊂VT×VG such that:
(A0) C∗∪{(LCA(πT(C∗)),LCA(πG(C∗)))}∈C(T,G);
(A1) C∗ is an anti-chain.
The intuition behind the definition of C∗(T,G) is that we are assuming that we already know argmin{∥C′∥∞∣C′∈CR(Tx,Gy)} for every x∈ET and y∈EG, and we use C∗∈C∗(T,G) to optimally aggregate these results to find the optimal global coupling between T and G. We formalize such an idea in the following definition.
Definition 14. Let Cx,y∈CR(Tx,Gy) for every x,y∈VT×VG. Given C∗∈C∗(T,G), with r=LCA(πT(C∗)) and r′=LCA(πG(C∗)), we define the extension of C∗ by means of {Cx,y}(x,y)∈C∗ as:
The set of all possible extensions of C∗ is called E(C∗). If Cx,y∈argmin{∥C′∥∞∣C′∈CR(Tx,Gy)} for all x,y, then we call the extension minimal. We collect all minimal extensions of C∗ in the set Em(C∗), which is never empty. If all Cx,y and e(C∗) are special couplings, then we call the extension special. We collect all special extensions of C∗ in the set Eo(C∗), which is never empty. We name Eom(C∗)=Em(C∗)∩Eo(C∗) the set of minimal special extensions of C∗; this set could be empty.
Since extensions are couplings, it is obvious that:
See also Figure 8(a). Moreover, it is also clear that any coupling is an extension of some C∗∈C∗(T,G) and, thus:
The upcoming theorem states that there are strong relationships between dI and extensions obtained via a fixed family of Cx,y∈CR(Tx,Gy).
Theorem 3. (Decomposition) Consider two merge trees T and G and take a collection {Cx,y}(x,y)∈VT×VG with Cx,y∈argmin{∥C′∥∞∣C′∈CR(Tx,Gy)}. Given C∗∈C∗(T,G), we name e(C∗) the extension obtained by means of {Cx,y}. We have:
Moreover, if Cx,y is also a special coupling for every x,y, we have:
We remark that Theorem 3 is in some sense unexpected: if Eqs (8.1) and (8.2) are in some sense trivial, Eqs (8.3) and (8.4) are not. We highlight that the couplings {Cx,y} are independently fixed at the beginning and not chosen with some joint optimization strategy. Moreover, the proof of Eq (8.4) depends strongly on the possibility to find optimal couplings which are also special.
9.
Bounding the interleaving distance
The aim of this section is to exploit the coupling formulation of the interleaving distance and its properties to find ways to get upper and lower bounds for dI. More in details: Section 9.1 resorts to pruning to reduce the complexity of the trees and finds upper bounds for dI, while Section 9.2 takes a more complex approach: via a recursive decomposition of couplings obtains lower and upper bounds for dI.
9.1. Pruning merge trees
We briefly introduce the pruning operator Pε. Given a merge tree T and ε>0, the merge tree Pε(T) is obtained through a recursive procedure: given a leaf x and its father x′, if f(x′)−f(x)<ε, we say that x is a small-weight leaf; we want to remove all small-weight leaves (unless two or more of them are siblings, i.e., children of the same father) and all degree 2 vertices from T. In this case, we want to remove all leaves but the one being the lowest leaf. To make this procedure well-defined and to make sure that, in the end, no small-weight leaves are left in the tree, we need to choose some ordering of the leaves and to resort to recursion.
(P) Take a leaf x such that f(father(x))−f(x) is minimal; if f(father(x))−f(x)<ε, remove x and its father if it becomes a degree 2 vertex after removing x.
We take T0=T and apply operation (P) to obtain T1. On the result, we apply again (P) obtaining T2, and we go on until we reach a fixed point Tn=Tn+1=Pε(T) of such sequence. To shed some light on this definition, we prove the following lemma; Figure 9 can be helpful in following the statements.
Lemma 3. Given T, ε>0, and Pε(T), we have a natural injective map VPε(T)↪VT which identifies vertices in Pε(T) with vertices in T. Call Cε⊂VPε(T)×VT the set of couples induced by VPε(T)↪VT. The following hold:
1) Cε is a coupling;
2) LPε(T)⊂LT, and for every v and v′ such that v′<v and f(v)−f(v′)≥ε, there is x∈LPε(T) such that LCA(x,v′)<v; in particular, argminf∈LPε(T);
3) For every v∈VT−VPε(T), we have #ΛTCε(v)≤1; in particular, if v∈DTCε, we have #ΛTCε(v)=0 and f(φCε(v))−f(v)<ε;
4) The map: ηCε:DTCε→VT such that f(ηCε(x))<f(x) for all x∈DTCε;
5) ∥Cε∥∞≤ε/2.
Having characterized the pruned trees with the above lemma, we can obtain the following proposition.
Proposition 4. Given two merge trees T and G, we have:
As a result, if the number of leaves of T and G is too high, we know that we can prune them, reducing the computational complexity of dI, to obtain an estimate from above of dI(T,G).
We close this section with a conjecture we would like to investigate in the future.
Conjecture 2. The coupling Cε is a minimizing coupling.
9.2. Recursive procedures for upper and lower bounds
In this section, we exploit Theorem 3 to obtain a dynamical approach to estimate, from above and below, an optimal coupling between two merge trees by solving recursively binary linear programming (BLP) problems.
9.2.1. Computing the cost of a coupling extension
As a first step, we separate the problem of finding C∗∈C∗(T,G) with a cost-minimizing extension into two "independent" problems: the first one is to find a minimal-fixed root coupling, and the second one is to compute the cost of deleting the vertices which are not in the subtrees whose roots are fixed by C∗. To make the upcoming lemma more clear, we establish the following notation. Suppose r=LCA(πT(C∗)) and r′=LCA(πG(C∗)). Then for v≰r, we set:
and fr=minv≤rf(v). Lastly, we define:
Note that Hr,r′ does not depend on the chosen extension of C∗, and, in fact, it depends only on r,r′. The upcoming lemma states that Hr,r′ accounts for the deletions of all the vertices which are not below r or r′.
Lemma 4. Consider T,G merge trees and C∗∈C∗(T,G), with r=LCA(πT(C∗)) and r′=LCA(πG(C∗)). Let Cr,r′ be any extension of C∗. With an abuse of notation, we consider C′r,r′ as the coupling in C(Tr,Gr′) consisting of the same couples as Cr,r′. Then,
If Cr,r′ is a special coupling, the inequality becomes an equality.
Since the computation of Hr,r′ can be easily accessed in a greedy fashion, from now on, we focus on estimating C∈argmin{∥C′∥∞∣C′∈CR(T,G)}.
9.2.2. Iterative approach
Now, we outline a procedure to estimate C∈argmin{∥C′∥∞∣C′∈CR(T,G)}. As in Theorem 3, we assume that we already have computed the couplings Cx,y∈CR(Tx,Gy) that we want to use to extend any C∗∈C∗(T,G), as in Theorem 3. So for instance, if we want to work with special extensions, we assume that we have Cx,y∈argmin{∥C′∥∞∣C′∈CoR(Tx,Gy)} for all x∈ET and y∈EG, and we exploit them to obtain a special extension of some C∗∈C∗(T,G). If we want to work with minimal extensions, instead, we assume to have Cx,y∈argmin{∥C′∥∞∣C′∈CR(Tx,Gy)}. We anticipate that both kinds of extensions are important for our purposes: special extension will be used to produce upper bounds for the interleaving distance, while minimal extension will be used, exploiting Theorem 3, to obtain lower bounds.
As before, we set: fx=minv≤xf(v) and gy=minw≤yg(w). Lastly, we fix a constant K>0 such that K>maxx∈VT,y∈VG∣f(x)−g(y)∣. In Section 9.2.5, we point out which steps of the upcoming procedure may produce errors.
9.2.3. Variables and constraints
We consider the following set of binary variables: ax,y for x∈ET and y∈EG; ux for x∈ET and uy for y∈EG. The vector of all variables (upon choosing some arbitrary ordering) will be referred to as V.
We also introduce the following auxiliary variables, which are linear functions of ax,y, ux, and uy:
● cx=∑yax,y and cy=∑xax,y;
● Λx=∑v≤xcv and Λy=∑w≤ycw;
● dx=∑v≤xcv+∑v>xcv and dy=∑w≤ycw+∑w>ycw.
Given such vatiable, we define the following linear constraints:
(1) For every l∈LT: ∑l≤x<rTcx≤1 and for every l′∈LG: ∑l′≤y<rGcy≤1;
(2) ux≤0.5Λx and uy≤0.5Λy for every x and y;
(3) ux≥mxΛx+qx and uy≥myΛy+qy for every x and y. With mx,qx being any pair of (m,q) such that the following are satisfied: q<0, m+q<0, 2m+q>0, m⋅(#LT)<1 (analogously for my,qy);
(4) (Only for special extensions) Let ˜x=argminv∈VTf(v) and ˜y=argminw∈VGg(w); then, we ask ∑˜x≤x<rTcx≥1 and ∑˜y≤y<rGcy≥1.
The set of vectors of variables which satisfy these constraints is called either Km(T,G) or Ko(T,G), depending on whether constraints (4) are, respectively, included or not. Note that Km(T,G)⊃Ko(T,G). To lighten the notation, we often avoid explicit reference to T and G when talking about the set of possible solutions, and, when we do not wish to distinguish between Km and Ko, we simply write K. Now, we briefly comment on the variables and constraints to try to give some intuition about their roles:
● The variables ax,y are used to match x with y, i.e., add the couple (x,y) to the coupling. In particular, constraints (1) ensure that, if V∈K, the set CV:={(x,y)∈ET×EG∣ax,y=1} belongs to C∗(T,G);
● The variables dx and ux are used to determine if x must be deleted. Start with dx. The main idea, which our optimization procedure is based on, is that if av,w=1 with v>x, it means that x is taken care of by the coupling Cv,w and, thus, we want to "ignore" such x. In other words, having dx=0 implies that x is deleted with #Λ(x)=0;
● Now, we turn to ux. Observe that, if Λx∈{0,1}, then ux=0 while if Λx≥2, ux=1. Note that Λx≤#LT and Λy≤#LG. Constraints (2) and (3) are fundamental to fix the value of ux, depending linearly on Λx: ux=1 if, and only if, x≥LCA(v,v′), with av,w=1 and av′,w′=1, for some w,w′∈VG. Thus, having ux=1 means that x is deleted with #Λ(x)>1;
● Lastly, we comment on constraints (4). These constraints are asking that there is one point above the lowest vertex in each tree which is coupled by CV; this in particular implies that, if we assume Cx,y∈Co(Tx,Gy), then ˜x and ˜y (with ˜x=argminv∈VTf(v) and ˜y=argminw∈VGg(w)) are never deleted. Thus, {(rT,rG)}∪(⋃(x,y)∈CVCx,y) is a special extension, i.e., a coupling in CoR(T,G).
As a consequence of these observations, any C∈C∗(T,G) induces a unique vector of variables V∈K, such that CV=C. Moreover, if Cx,y∈Co(Tx,Gy) and V∈Ko, then {(rT,rG)}⋃(x,y)∈CVCx,y is a special extension of CV.
9.2.4. Objective functions
A key fact that we highlight is that, by property (A1), if x=LCA(v,v′), with av,w=1, av′,w′=1 and x<rT, then δ(x)=rT due to the anti-chain condition. So, we know that any vertex x′ such that x≤x′<rT, is in DTCV. Thus, given x∈VT, and with xf being its father, the "local" objective function depends on the following quantities:
● ∑yax,y∥Cx,y∥∞: it is the cost of matching Tx and a subtree Gy′, for some y′, if (x,y′) is added to C, i.e., if ax,y′=1. If Cx,y′ is not a minimal coupling, this is an upper bound;
● ∣g(rG)−f(x)∣ux: it is an upper bound to the cost of deleting x, with #Λ(x)>1;
● Ax=0.5(f(xf)−fx)(1−dx): in case x is deleted with #Λ(x)=0, it gives a lower bound to the deletion of Tx, as it is equal to deleting the lowest point below x to the height of the father of x, in two step. It is an exact value if xf=φ(x) and g(η(x))−fx<Ax;
● Bx={∑yav,y(gy−fx)−Kdx}v∈ET,v<xf: in case x is deleted with #Λ(x)=0, it helps giving an upper bound to the deletion of Tx, depending on what happens below xf. If there is v<xf such that v is coupled with y and Cx,y is a special coupling, then we know that gy≥g(η(x)), and so gy−fx≥g(η(x))−fx. Thus, if Cx,y is a special coupling, max{maxBx,Ax}≥cost(x).
For any x∈ET, we define:
similarly, for any y∈EG:
In full analogy, we set:
and
for any y∈EG.
Lastly, Γ↑(rT):=Γ↓(rT):=∣rT−rG∣.
With an abuse of notation, we write:
Note that all the functions we defined in this section depend on T, G, and on the family {Cx,y}(x,y)∈VT×VG, but we avoid explicit reference to those dependencies for notational convenience.
We sum up the main properties of the definitions we have just stated with the following proposition.
Proposition 5. Given C∈C∗(T,G) and Cx,y∈CoR(Tx,Gy) for all (x,y)∈C, we call:
If Co is a special extension, then:
with V being the unique vector in Ko such that CV=Co.
Vice versa, given C∈C∗(T,G), and Cx,y∈CR(Tx,Gy) with minimal cost for all (x,y)∈C, we call
Then,
with V being the unique vector in Km such that CV=Cm.
Putting together Theorem 3 and Proposition 5, we obtain as a corollary:
Corollary 2. Consider T,G merge trees, and take for every (x,y)∈ET×EG:
1) Cx,y∈argminC′∈CR(Tx,Gy)∥C′∥∞;
2) C′x,y∈argminC′∈CoR(Tx,Gy)∥C′∥∞.
Then,
where Γ↓ is computed with the collection {Cx,y} and Γ↑ is computed with the collection {C′x,y}.
Now, we get rid of the fixed roots, obtaining an approximation for dI(T,G) by putting together Theorem 3, Lemma 4, and Proposition 5. To do so, we consider (x,y)∈ET×EG, take the subtrees Tx and Gy, and apply the framework introduced in Section 9.2.3 and Section 9.2.4, replacing T and G with, respectively, Tx and Gy. We write Km(x,y), Ko(x,y), Γ↓(x,y), and Γ↓(x,y) to imply that the constraints and the objective functions are defined using the subtrees Tx and Gy. To lighten the notation, we simply write V to identify the optimization variables. In other words, when we write Γ↑(x,y)(V), we are implying V∈Ko(x,y), etc.
Corollary 3. In the same setting as Corollary 2, for each (x,y)∈VT×VG, we have:
where Γ↓(x,y) is computed with {Cx,y} and Γ↑(x,y) is computed with {C′x,y}.
Consequently,
9.2.5. Estimation errors
We take this section to briefly isolate which are the situations in which the procedure outlined in Section 9.2.3 and Section 9.2.4 may produce errors, w.r.t. the true interleaving distance.
1) ∣g(rG)−f(x)∣ux: clearly, rG (resp., rT) is an upper bound for χ(x) (resp., χ(y)) with x (resp., y) being deleted with #Λ(x)>1 (resp., #Λ(y)>1), and so ∣g(rG)−f(x)∣ux is an upper bound to the cost of the corresponding deletion.
2) Bx′: for v∈DT with #Λ(v)=0, x=φ(v), and x=father(x′), we may have ∣f(v)−g(η(v))∣≤maxBx′.
We point out two facts. First, Γ↓ does not involve any of the aforementioned situations. Second, in the definition of Γ↑, the biggest potential source of error are the terms ∣g(rG)−f(x)∣ux, which can overestimate the cost of deleting internal vertices in order to swap father-children relationships. We point out that metrics for merge trees like [43,48], even in their unconstrained formulation, do not even account for the possibility of deleting internal vertices in order to swap father-children relationships. Because of this, they are unstable and authors resort to preprocessing strategies, trying to make up for this source of instability. See also [41] for more details. Also, replacing ∣g(rG)−f(x)∣ux with the exact deletion cost would turn the linear optimization problem into a polynomial one.
9.2.6. Linearization
In Section 9.2.3, we have introduced a set of linear constraints needed to optimize a nonlinear function (either Γ↑ or Γ↓) of the form minV∈KmaxiFi(V) for some real-valued functions Fi which are linear in V. See Section 9.2.4. We can turn this into a linear optimization problem by exploiting a standard trick, introducing auxiliary variables and additional constraints.
Suppose we need to find minsmax(f(s),g(s)), with f,g functions of s. We introduce the variable u, with the constraints u≥f(s) and u≥g(s), and then solve the linear problem mins∈Rn,u≥f(s),u≥g(s)u, with n equal to the number of constrains. We want to use this procedure to compute minV∈KΓ↑(V) and minV∈KΓ↓(V). We write down the details only for minV∈KΓ↑(V), and the case for Γ↓(V) follows analogously.
Given x∈ET, we define F1x=∑yax,y∥Cx,y∥∞, F2x=(g(rG)−f(x))ux, and F3x=Ax. Given y∈EG, instead, we set F1y=(f(rT)−g(y))uy, and F2y=Ay. Analogously, we have F1rT=∣f(rT)−g(rG)∣. Having fixed a total ordering on VT={a0,…,an} and VG={b0,…,bm}, respectively, we call F the vector containing all the components Fix and Fjy of all the points taken in the chosen order:
for some set I1 indexing the components of F.
Similarly, for every x, we order the elements of the set Bx, so that we can write Bx as a vector Bx=(B1x,…,Bhx,…), then we define the vector:
for some set I2 indexing the components of B.
Lastly, we introduce the real valued auxiliary variable z and add the following linear constraints to the ones presented in Section 9.2.3:
(5) z≥Fi(V) for all i∈I1;
(6) z≥Bi(V) for every i∈I2,
and then solve minz,Vz with all these constraints. We call Z(V) the set of admissible values defined by constraints (5) and (6), as a function of V.
We stress again that Fi and Bi are linear in V; so the final problem is linear with mixed binary valued variables. In case of Γ↓, we repeat the same operations, omitting the constraints in (6).
9.2.7. Bottom-Up algorithm and computational complexity
In this section, the results obtained in Section 8 and the formulation established in the previous parts of Section 9 are used to obtain the algorithm implemented to estimate the metric dI between merge trees. We need to introduce some last pieces of notation in order to describe the "bottom-up" nature of the procedure.
Given x∈VT, define lenT(x) to be the cardinality of {v∈VT∣x≤v≤rT} and len(T)=maxv∈VTlenT(v); similarly, lvlT(x)=len(T)−lenT(x), and so lvl−1T(n)={v∈VT∣lvlT(v)=n}.
The key property for our bottom-up procedure is that: lvlT(x)>lvlT(v) for any v∈subT(x). Thus, we will compute some quantity ˜W↑x,y for some x∈lvl−1T(n) and y∈lvl−1G(m), assuming that we will have already computed ˜W↑v,w for all v, w in VT, VG such that lvlT(v)<n and lvlG(w)<m. We write down Algorithm 1, which refers to the computation of minΓ↑. Note that thanks to constraints (4) this recursive procedure is always guaranteed to provide a special coupling. However, clearly, not all special couplings satisfy constraints (4).
For a couple (x,y)∈VT×VG, we write ˜Z↑(x,y)(V) to indicate the set of admissible values as a function of V, described by constraints (5) and (6), where the functions Fi and Bi are given by the components of Γ↑(x,y), apart from Fv1=∑w∈EGyav,w∥Cv,w∥∞, which is replaced by some quantity ∑w∈EGyav,w˜W↑v,w we will define in the upcoming lines. In particular, ˜W↑v,w, which we will have computed at iterations prior to the one involving (x,y), is an estimate of ∥Cv,w∥∞. See Algorithm 1.
The case for Γ↓ follows the same algorithm, but instead of ˜W↑x,y, we have:
where ˜Z↓(x,y)(V) stands for the set of admissible values described by constraints (5), with the functions Fi given by the components of Γ↓(x,y), apart from Fv1=∑w∈EGyav,w∥Cv,w∥∞, which is replaced by ∑w∈EGyav,w˜W↓v,w for every v∈ETx. By Section 9.2.5, such a recursive procedure produces no error when replacing Fv1 with ∑w∈EGyav,w˜W↓v,w.
In other words, for any collection Cx,y∈argminC∈CmR(Tx,Gy)∥C∥∞, with (x,y)∈ET×EG, we have:
giving a valid lower bound for dI. Similarly, since constraints (4) are not satisfied by all special couplings, given any collection C′x,y∈argminC′∈CoR(Tx,Gy)∥C′∥∞, with (x,y)∈ET×EG, we have:
giving a valid upper bound for dI.
9.2.8. Error propagation
We make a brief observation to take care of the interactions arising between the estimation errors described in Section 9.2.5 and the bottom-up procedure proposed in Section 9.2.7.
Consider the setting of Section 9.2.4 and suppose that, instead of having computed the optimal couplings Cx,y, we have some nonoptimal C′x,y as it is the case for W↑x,y and ˜W↑x,y - with an error bound ex,y such that ∣∥Cx,y∥∞−∥C′x,y∥∞∣<ex,y. We immediately see that the errors ex,y affect only the components of the form ∑yax,y∥C′x,y∥∞, as these are the only parts of the optimization procedure which depend on ∥C′x,y∥∞. Moreover, the potential errors occurring in Γ↑ and Γ↓, appear at the level of Bx and ux (see Section 9.2.5), but ux and Bx do not depend on ∥C′x,y∥∞ nor on ux′ and Bx′, for some other x′. This implies that the only interaction between errors is of the form max{a,b}, but they never aggregate in any way in the objective functions. Thus, the final error in the algorithm presented in Section 9.2.7 is the maximum of all the "independent" errors occurring at every iteration.
9.2.9. Computational complexity
Proposition 6. (Computational cost) Let T and T′ be two merge trees with full binary tree structures with dim(T)=#ET=N and dim(T′)=#ET′=M.
Then,
● to compute ˜W↑x,y for every (x,y)∈ET×ET′ with Algorithm 1, we need to solve O(M⋅N) mixed binary linear optimization problems, with O(M⋅N) variables and O(M⋅log2(M)+N⋅log2(N)) linear constraints;
● to compute ˜W↓x,y for every (x,y)∈ET×ET′ with Algorithm 1, we need to solve O(M⋅N) mixed binary linear optimization problems, with O(M⋅N) variables and O(log2(M)+log2(N)) linear constraints.
Proof. In a full binary tree structure, at each level a, we have 2a vertices. Let A=len(T) and A′=len(T′). We have that, for any vertex v∈VT at level a, the cardinality of the path from v to any of the leaves in subT(v) is A−a and the number of leaves in subT(v) is 2A−a. The number of vertices in subT(v) is instead 2A−a+1−1 and the number of edges 2A−a+1−2.
Consider v∈VT at level a and w∈VT′ at level a′. According to Section 9.2.3 to compute Γ↑ with Tv and T′w, we need (2A−a+1−2)⋅(2A′−a′+1−2)+2A−a+1−2+2A′−a′+1−2 binary variables and 2A−a+2A′−a′+2⋅(2A−a+1−2)+2⋅(2A′−a′+1−2) linear constraints (if we consider constraints (1)–(3) in Section 9.2.3) in the nonlinear problem. Constraint (4) adds just 1 further constraint, so we can ignore it. To linearize the problem, we need to add 1 real valued auxiliary variable and 3⋅(2A−a+1−2)+2⋅(2A′−a′+1−2) constraints to take into account for the set F and additional:
constraints for the set B. Simplifying, we have: (a+1)⋅(2A−a+1−1)+(a′+1)⋅(2A′−a′+1−1)≤O(2A+2A′) constraints for B.
Putting the things together we have:
binary variables and
linear constraints.
Thus, to minimize Γ↑, we need to solve (2L+1−1)⋅(2A′+1−1) linear binary optimization problems, each with 2A⋅2A′+O(A+A′) variables and O(2A+2A′) constraints. Instead, for Γ↓, we need to solve (2A+1−1)⋅(2A′+1−1) linear binary optimization problems, each with 2A⋅2A′+O(A+A′) variables and O(A+A′) constraints. Substituting A=log2(N) and A′=log2(M) in Eqs (10) and (11) gives the result. □
We highlight that the classical edit distance between unlabeled and unordered trees, obtained with BLP [31], can be computed by solving O(N⋅M) BLP problems with O(N⋅M) variables and O(log2(M)+log2(N)) constraints, O(N+M) if we count also the constraints restricting the integer variables to {0,1}, as the authors of [31] do. Thus, the approximating procedures we developed are not far from the computational complexity of the renowned tree edit distance: min˜W↑x,y differs by some linear factors while min˜W↓x,y has the same complexity.
As already mentioned, most of the edit distances for merge trees, in their unconstrained formulation, have equal or higher computational complexity w.r.t. the classical edit distance between unlabeled and unordered trees. Thus, the fact that the authors of those metrics obtain polynomial-time algorithms under constrained formulations supports our conjecture that a similarly constrained formulation of the interleaving distance could yield practically useful polynomial bounds.
In Appendix B, we provide a comparison between the computational complexity of our methods and those presented in [3] and [25].
10.
Simulations and case studies
In this section, we extensively look at the practical behavior of the upper and lower bounds of dI that we obtained in Section 9.2. We name du(T,G) the upper bound obtained with Algorithm 1, and dl(T,G) the lower bound obtained with the analogous algorithm. Generally speaking, we aim at showcasing that we can use du in many practical scenarios, and we have a number of tools at our disposal to check the reliability of the obtained results. More in details:
● We use the upper bound du as reference estimate of dI: we compare it with the upper bound developed in [16], use it to analyze datasets, etc.;
● We use the lower bound dl and the bottleneck distance between persistence diagrams to find the potential error range of the computed upper bound, exploiting the fact that dB≤dI [9]. More precisely we check the relative discrepancy:
With this quantity, we can obtain an upper bound on the error between dI and du via du−dI≤Δ⋅du;
● We use the sup norms between the considered functions to check if du shows instances of unstable behavior, i.e., du(Tf,Tg)>∥f−g∥∞.
We perform three kinds of simulations: in Section 10.1, we compare our estimates of dI with the method presented by [16], which, to the best of our knowledge, is the only publicly available code to estimate dI; in Section 10.2, we look at the empirical stability of du by checking how adding pointwise noise to a smooth function is reflected on the associated merge trees in terms of du; in Section 10.3, we tackle some benchmark classification case studies involving some functional datasets.
10.1. Comparison with [16]
The method proposed by [16] turns the unlabeled problem of the interleaving distance between merge trees into a labeled interleaving problem by proposing a suitable set of labels. The optimal labeling would give the exact value of the interleaving distance, but, in general, this procedure just returns an upper bound. We call dlab the upper bound obtained with the labeled method proposed by [16].
For any fixed i, we generate a couple of point clouds Cki={(xkj,ykj)∣j=1,…,ni}⊂R2, with k=1,2, according to the following process:
where N(μ,σ) indicates a Gaussian distribution.
Note that ni regulates the number of leaves in the trees (which we fix before sampling Cki). From Cki we obtain the single linkage hierarchical clustering dendrogram TCki (that is, the merge tree representing the Vietoris Rips filtration of Cki), and then compute du(TC1i,TC2i), dl(TC1i,TC2i), and dlab(TC1i,TC2i). The distance dlab is computed with the code available at https://github.com/trneedham/Decorated-Merge-Trees, while du is computed via the procedure described in Section 9.2.7. For each ni∈{3,…,15}, we sample 100 pairs of point clouds and then, similarly to Eq (10.1), compute the relative difference between the two estimates: (dlab−du)/du. Note that there are no absolute values.
We repeat the same experiment, this time with ni∈{100,...,109}. Since in this case du requires too much time to be computed exactly, we exploit Proposition 4 and consider the smallest ε>0 such that Pε(TC1i) and Pε(TC2i) have fewer or equal than 15 leaves. We then call dopt(TC1,TC2)=max{ε/2,du(Pε(TC1),Pε(TC2))}.
For ni∈{100,...,109}, we compute the relative difference between dlab and dopt with the formula: (dlab−dopt)/dopt. Note, again, that there are no absolute values.
The results of the simulations can be seen in Figure 10. Looking at Figure 10, we see that, in the context of our data-generating process, the estimate given by dlab is very unreliable, overestimating dI by a median of at least 50–60% of its actual value; in particular, there are some outliers which are completely off, even w.r.t. the values obtained with du and dopt, with errors of more than 3 times the actual value.
The estimates obtained with du in this simulation have a negligible difference with the actual values of dI: across all ni∈{3,…,15}, the maximum value of the relative difference Δ between du and dl was 10−7. Note that, for the other values of ni, we cannot give a lower bound using dl on the pruned trees.
As a conclusive remark, we say that the computational advantages of the labeled approach are immense and potentially adequate even for real-time applications, but from our simulation, we see that the results need to be taken with care, for the estimates produced are not always good. On the other hand, with the present implementation, the computational cost of our approach becomes prohibitive quite quickly as the number of leaves in the trees increases, even if there might be situations like the one in this simulation in which the scheme we used for ni≥100 can produce good estimates. We think that interactions between the two approaches could lead to substantial speed-ups: being able to fix the value of some variables in our algorithm exploiting the labeling scheme by [16] could greatly reduce the dimensionality of the problem and, thus, its computational cost.
10.2. Noisy functions
Now, we want to verify, experimentally, if du retains good stability properties w.r.t. the universal stability properties of the interleaving distance.
To do so, we pick a standard model in functional data analysis and look at how the distance between the merge trees associated to noisy observations and the original smooth function behave as we increase the noise in the model. Roughly speaking, the model considers a smooth function f, randomly sample a set of points in the domain where we evaluate f, and add pointwise noise to these values. The final set of couples is a single datum in the generated dataset.
We generate f by interpolating, with cubic splines, a set of randomly chosen couples in [0,1]×R. The distribution that we use to sample this set of couples is the following: we take 0=x1<…<xN=1, N=20, forming a regular grid in [0,1]. Then, yi, i=1,…,N, are sampled independently from a Gaussian with mean 0 and standard deviation 50. The couples {(xi,yi)}i=1,…,N are interpolated to obtain f. Other methods to sample a smooth function could be employed as well.
We sample the noisy observations of f according to the following model, which belongs to a family of standard models for functional data (see [45]). We name such model (Mσf).
(Mσf) Let X be a random variable distributed with uniform density on [0,1], and consider the random variable Y such that Y∣X=x∼f(x)+ϵ, with ϵ being an independent Gaussian with mean zero and standard deviation σ.
We obtain each of our partially observed noisy functions drawing i.i.d. samples from (Mσf). Specifically, for each value of σ∈{0.1,1,10,15,25}, we sample a dataset Dσ where each of the 100 i.i.d. observations (i.e., each partially observed function) is obtained by sampling independently n=50 couples from (Mσf).
We compute the merge tree Tf of the smooth function f via linear interpolation of {(˜xi,f(˜xi))}i=1,…,300, with {˜xi}i=1,…,300 being a uniform grid on [0,1]. Then, for each {(ai,bi)}ji=1,…,50∈Dσ, j=1…,100, we compute the merge tree of the linear interpolation of the sampled couples without extending it to the whole interval [0,1], and we estimate, via du and dl, the interleaving distance between the merge tree obtained from the smooth f and from the noisy observation. As σ, which controls the magnitude of the noise, increases, we are interested in observing the behavior of the distance between the observed and the true merge trees. The sampled partial observations of functions have also been extended on [0,1] via a nearest value extension (NVE) technique, both for plotting purposes and to compute the sup norm between the extended functions, to check the stability of the upper bound du. See Figure 11.
To better portrait the stability of du, we benchmark our upper bound against a metric for merge trees with very different stability properties: the edit distance dE defined in [41]. Such edit distance can be computed exactly with a computational complexity similar of the ones of the upper and lower bounds we develop in this work, and satisfies the inequalities:
This implies that dE can grow linearly with the size of the trees.
Figure 11(d) summarizes the behavior of du and dE in response to increasing levels of noise. More precisely:
● The orange line interpolates, for each value of σ, the median of:
● The green line interpolates, for each value of σ, the median of:
● The blue line interpolates, for each value of σ, the median of:
The vertical bars in Figure 12 represent 1.5 times the interquartile range (IQR) below and above the median (i.e., the boxplots). In other words, we are checking how far from the true merge trees the observed merge trees tend to fall, as noise increases, where far is either in terms of du or dE. This is precisely where stability properties become crucial, as they provide robustness to support the analyst's findings.
For a reference, we also report the plot of the line (σ,6σ): we know that for every (X,Y) distributed according to model (Mσf), P(Y∈(f(X)−3σ,f(X)+3σ)∣X=x)∼1, for every x∈[0,1]. In particular, for {(Xi,Yi)}i=1,…,50 i.i.d., we have P(maxi=1,…,50∣Yi−f(Xi)∣<6σ)∼0.9. In other words, [0,6σ] is a 0.9 confidence interval for the max difference between the smooth functions and the noisy observations on the grid given by the realizations of {Xi}i=1,…,50. Note that, despite this, outside such grid, i.e., outside the points were the functions are observed, the error between the smooth functions and the extended noisy observations can be higher. Still, the line (σ,6σ) can serve as a rough reference for the pointwise difference between the smooth functions and the noisy observations.
In Figure 12, we see that the deviation between the true and the observed merge trees behave as we would expect: the deviation in terms of du increases with the magnitude of the noise σ, being controlled by the sup norm between the smooth functions and the extension on [0,1] of the noisy observations. The deviation in terms of dE, instead, explodes as σ increases, as dE depends on a combination of 1) the magnitude of noise and 2) the number of oscillations in the functions. When sampling and interpolating the partial and noisy observations of f, we are also potentially increasing the number of oscillations of the data w.r.t. the original f: while Tf has 5 leaves, for σ=0.1, the number of leaves ranges from 8 to 4, with a median of 6; for σ=1, the number of leaves ranges from 12 to 4, with a median of 9; for σ=10, the number of leaves ranges from 18 to 9, with a median of 14; for σ=15, the number of leaves ranges from 19 to 11, with a median of 15; for σ=25, the number of leaves ranges from 19 to 11, with a median of 15. Note that, at most, we can have 19 leaves, given that we sample on a grid of 50 points.
All of what we just said is coherent with the behavior we observe in Figure 12. The line (σ,6σ) further supports the coherence of our findings: for small values of σ, the error introduced by having to extend the observed values from a random grid to [0,1] overshadows the pointwise error; meanwhile, for σ=25 we see that the whole boxplot of the sup norms is below the dashed line.
To conclude this simulation, we double-check the results we obtained with du by computing also the relative discrepancies with dl, i.e., Δ, as in Eq (10.1). In Table 1, we report some percentiles - 95th,90th,85th,80th of the values Δ as a function of σ, showing that in most cases we have negligible uncertainties in our computations. As σ increases, some non-negligible discrepancies start to appear in a limited number of calculations. However, even in the worst case scenario, 85% of the distances still have a relative discrepancy between du and dI, which is guaranteed to be lower than 6%. No unstable behaviors of du, i.e., instances of du(Tf,Tg)>∥f−g∥∞, were registered. As a result, we can look at the results of this simulation with a very high level of confidence.
10.3. Case studies
Having tested du (and dl) in some controlled, simulated scenarios, now we test it on some benchmark functional datasets, tackling some classification problems.
The datasets we considered are suitable for our purposes for three reasons:
1) They are freely available and easily accessible via the scikit-fda python package [44];
2) Their complexity (in terms of number of statistical units, and number of oscillations of each function) allows the use of our estimation algorithms;
3) We can use the sup of the difference between the functions to check the stability of du.
To further validate our results, we build two kinds of alternative pipelines: a first one obtained by replacing du between merge trees, with dB between the associated persistence diagrams; and a second one using directly the original functions. The general pipeline we follow for du and dB is the following: we compute merge trees/diagrams, take pairwise distances, fit an embedding of the resulting metric space into an Euclidean space Isomap [6], and use quadratic discriminant analysis (QDA) on the embedded vectors. Since all the functions in each dataset are evaluated on the same grid, we also fit some "Baseline" pipelines, obtained by reducing the vectors' dimensionality with principal component analysis (PCA), to avoid overfitting, and using QDA directly on the resulting vectors. The parameters for the Isomap embeddings (the dimension and the number of points in a neighborhood) and the dimension of the PCA have been selected using leave-one-out cross validation, maximizing accuracy. We report the parameters and the results of the best performing models in Table 2.
We emphasize that the goal of these simulations is not to promote TDA tools over classical statistical methods, but rather to illustrate the practical behavior of our computational procedures and provide a blueprint for their application. In this regard, comparing du and dl with more traditional and arguably more suitable approaches offers a grounded assessment of their effectiveness. Additionally, we investigate whether the theoretical inequality dB≤dI [9], which suggests that dI has greater discriminative power than dB, also holds practical significance in these benchmark scenarios.
Accordingly, the selected datasets were not chosen specifically for their suitability to TDA techniques. This contrasts with applications such as those in [42], where functions must be analyzed up to warpings or re-parametrizations (see also [36]). In such cases, it has been shown that classical methods require complex and cumbersome pipelines to achieve reliable results, whereas the straightforward TDA approaches used here remain effective.
The datasets and the corresponding data analysis problems we consider are the following:
● "Octane" dataset [24]: contains near infrared spectra of gasoline samples, with wavelengths ranging from 1102nm to 1552nm with measurements every 2 nm; it contains six outliers to which ethanol was added, as sometimes required by some regulations. We want to build a classifier able to perform outlier detection. The dataset contains 39 observations, with 6 outliers, and the resulting merge trees have between 4 and 5 leaves, with a median of 4 leaves. In Figure 13(a), we see that there is clear separation between the outliers and the other data. Coherently, Table 2 shows that all the different models we considered successfully achieved this task;
● "NOx" dataset [26]: contains hourly measured daily nitrogen oxides (NOx) emissions in the Barcelona area. Since NOx causes ozone formation and contributes to global warning, it is of interest the identification of days with abnormally large emissions to allow the implementation of actions able to control their causes, which are primarily the combustion processes generated by motor vehicles and industries. The observations are labeled depending on if the emission curve was recorded during working days or during the weekend. We aim to reconstruct this labeling via a supervised classification problem. The dataset contains 115 observations, with 79 working days and 39 non-working days, and the resulting merge trees have between 2 and 9 leaves, with a median of 5 leaves. In Figure 13(b), we can visually appreciate that the problem is more challenging compared to the previous one. Despite that, Table 2 shows that we achieve very high accuracy, in cross-validation, with our pipelines, with the baseline approach outscoring the TDA one, and persistence diagrams achieving slightly better results than merge trees;
● "Growth" dataset [50]: is a popular dataset in functional data analysis, often referred to as "The Berkeley Growth Study", which contains the height measurements (in cm) of 54 girls and 39 boys between the ages of 1 and 18 years, see Figure 13(c). This dataset has been considered by a number of works, including works dealing with the problem of aligning/re-parametrizing the growth curves, factoring out of the analysis the "personal biological clock" [51] of each individual, to be able to more clearly identify any growth patterns in the data. See [51] and references therein. One interesting problem, often considered, is to compute the first derivative of the growth curves and try to recognize the different growth dynamics between boys and girls. This is also what we do: we smooth the functions via some kernel smoother (with a bandwidth of 3 and with the same kernel employed in [42]), consider the numerical derivatives of the smoothed curves, and try to discriminate boys from girls. The dataset contains 93 observations, 54 girls and 39 boys, and the merge trees of the derivatives have between 4 and 9 leaves, with a median of 5 leaves. In Table 2, we see that all the models achieve good results on this data, with the baseline being the best performing model and merge trees outscoring persistence diagrams;
● "Tecator" dataset (https://lib.stat.cmu.edu/datasets/tecator): this publicly available data is collected by a tool called "Tecator Infratec Food and Feed Analyzer", working in the wavelength range 850–1050 nm by the near infrared transmission principle, see Figure 13(d). Each sample contains a curve extracted from meat with different moisture, fat and protein contents. Many different data analysis questions and problems can be set up with this data. Relying on the derivatives of the curves, we consider the problem, as in [27], to discriminate between the curves coming from high fat meat (i.e., fat content >20) and low fat meat (i.e., fat content ≤20). The dataset contains 215 observations, 77 high fat samples, and 138 low fat samples, and the merge trees of the derivatives have between 2 and 10 leaves, with a median of 5 leaves. Table 2 reports the cross-validation accuracy of the classification models. We see that the TDA approaches, both with du and dB, outperform the baseline model, with merge trees again doing slightly better than persistence diagrams.
● "Beef" dataset [5]: contains five classes of mid-infrared spectrograms of beef, taken from a total of 60 cooked samples of minced silverside cuts with different kinds of adulterations, ranging from pure beef to beef adulterated with four different types of offal. This dataset is more complex than the previous ones, especially in terms of the number of oscillations of the spectrograms, with the corresponding trees ranging from 30 up to 64 leaves. As a consequence, we have resorted to the approach presented in Section 10.1, computing dopt instead of du, pruning merge trees so that they are left with at most 14 leaves. Most of the pruned trees have 14, leaves, while approximately 1/3 of the trees have 13 leaves, and two have 12 leaves. The leave-one-out results of this classification case study are reported in Table 2 and show that merge trees perform very similarly to the Baseline method, doing much better than persistence diagrams.
In the first four datasets, du gives very good estimates of dI, with Δ being less than 0.008 for 95% of the computed distances in each dataset. We did observe, for the "Tecator" dataset, 7 instances of du exceeding ∥⋅∥∞. Since the values by which du exceeded ∥⋅∥∞ were always below 10−8, we believe it is due to numerical errors. For the "Beef" dataset, we cannot give lower bounds, but we checked for unstable behaviors of dopt, and none were recorded.
To conclude, we have shown several case studies in which du produced reliable estimates of dI, validated by controlling the outputs with lower bounds (via dl and dB) and upper bounds (via ∥⋅∥∞). The results obtained via the implemented pipelines were bench-marked against established TDA and classical tools, showing equal or superior performances w.r.t. persistence diagrams in all but one situation.
11.
Conclusions
In this work, we introduced a novel graph-matching formulation for the interleaving distance between merge trees, leveraging global matchings rather than the traditional approach based on ε-good maps. This reformulation not only provides a new perspective on the metric but also facilitates computational advancements by enabling recursive decomposition techniques and constrained formulations inspired by the literature on edit distances. As a first practical result of our approach, we propose upper and lower bounds using a dynamic linear binary programming framework.
While we leave to future works the problem of adapting the dynamic linear binary programming algorithm to the constrained interleaving distance, conjecturing that it would result in a polynomial time upper bound, our empirical evaluation demonstrated that the presented approach reliably estimates the interleaving distance and provides more controlled error estimates compared to existing methods. Through a comprehensive set of case studies, we validated the practical efficacy of our bounds by benchmarking them against both traditional TDA methods and classical statistical approaches.
However, our method also comes with computational trade-offs: the reliance on integer programming comes with a high computational burden, making the approach suitable only for small to moderately sized datasets. Another drawback of the presented approach is that it only provides a-posteriori error bounds: we don't have methods to provide the reliability of our tools before actually computing the distance, or for calibrating their precision. In particular, it is not possible to set an arbitrary precision level by choosing the value of some parameter.
On top of the aforementioned research direction aiming at proving theoretical and computational properties of the constrained interleaving distance, our findings also suggest some additional directions. The relationship between optimal couplings and continuous monotone maps, as highlighted in Section 6, hints at yet another possible formulation of the interleaving distance purely in terms of metric tree mappings. Given that this is among the first works practically employing the interleaving distance, further comparisons between the interleaving distance and other merge tree distances could help elucidate their respective stability and sensitivity properties in different data analysis contexts.
In conclusion, our work provides both theoretical advancements and practical tools for computing and understanding the interleaving distance. Even if computational efficiency remains a challenge, we have provided effective tools to work in small-data regimes, and we believe that we have laid out the main steps for finally making the interleaving distance a disposable tool for analyzing data in topological data analysis.
Use of Generative-AI tools declaration
The author declares that he have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work was carried out as part of my PhD Thesis, under the supervision of Professor Piercesare Secchi. The author also acknowledge the support of the Wallenberg AI, Autonomous Systems and Software Program (WASP), and of the SciLifeLab and Wallenberg National Program for Data-Driven Life Science (DDLS), which fund the project: Topological Data Anlysis of Functional Genome to Find Covariation Signatures.
Conflict of interest
The author declares no conflict of interest.
A.
Notation and flowcharts
To facilitate navigating through the manuscript, we prepared some flowcharts (Figure 14), and a table (Table 3), summarizing the structure of our theoretical investigation and the most important pieces of notation we introduce.
B.
Comparison with [3] and [25]
We now discuss the computational complexity and practical performance of our algorithms in comparison to those developed in [3] and [25]. To begin with, we note that, to the best of our knowledge, no public implementations of the latter two algorithms are currently available. As a result, we do not provide a case study to evaluate their runtimes or the reliability of their approximations. Similarly, the original works do not include any examples or simulations.
Moreover, these algorithms differ significantly in nature: ours is a BLP-based estimation algorithm equipped with a posteriori error bounds; [3] offers an approximation within a tree-dependent multiplicative factor; and [25] presents an exact fixed-parameter tractable (FTP) algorithm. Given these fundamental differences, making a direct comparison is far from straightforward.
Nonetheless, we attempt a comparison based on both theoretical and practical considerations, focusing on selected cases that, while specific, remain meaningful and illustrative.
We start by focusing on the algorithm in [25]. The authors of [25] show that determining if dI(T,G)≤k, can be run in O((N+M+2)2log3(N+M+2)22τττ+2) (with N,M being as in Proposition 6), where τ depends on k, T, and G. Thus, in order make some explicit computations, we pick a situation in which we can parametrize τ in terms of tree complexity. To such extent, we consider a merge tree T with full binary tree structure, as in Proposition 6. We denote this tree by Tl, where l=len(Tl), and we assume that the height difference between each node and its child is exactly 1. In other words, the structure of Tl is fully described by l. Since each internal vertex has degree 3, for each k<l, we have τ(k)≥3⋅2k+1. In fact, k-balls, as defined in [25], are full binary trees of length k. Note that this is neither a worst-case scenario nor a best-case scenario analysis: it is just a reference situation in which we can make some explicit computations. For instance, having the length of the edges decay as lvlTl(v) grows would yield bigger values of τ(k).
Suppose that we want to check if the interleaving distance is bounded from above by k=1,2,3,4,5. Then, the leading coefficient in the computational cost is, respectively, at least 1018,1043,1098,10223,10501, which then needs to be multiplied by (N+M+2)2log3(N+M+2). Note that for k=5, regardless of G, it is already challenging to compute the complexity of the algorithm, let alone running the algorithm itself to decide if dI(Tl,G)≤k. Plus, we point out that if G has one leaf, we have dI(Tl,G)=l, and having l=4,5 is well within the range of complexity contained in our runtime simulations. See Appendix C.
To conclude this first comparison, we offer a complementary perspective by referencing an FTP algorithm developed in [4] for a specific edit distance between trees. More precisely, [4] addresses the computation of the edit distance between unordered, labeled trees with positive integer costs.
We stress that the following discussion is intended as a rough, qualitative comparison: to establish a meaningful basis for comparison between the algorithm in [25] and the one in [4], we will consider additional specific scenarios that help align the assumptions and problem settings of the two approaches.
This comparison is motivated by the following considerations:
1) In Section 9.2.9, we show that computing min˜W↓x,y is as expensive as computing the tree edit distance between two unlabeled weighted trees (with the same tree structures as the trees considered to compute the interleaving distance). Plus, the edit distance between unlabeled weighted trees can be framed as an edit distance between unordered labeled trees by setting relabeling, insertion, and deletion costs equal to the absolute difference between the weights of the involved edges (or zero, if only one edge is involved), and making sure that the labels sets of the two trees are disjoint;
2) To the best of our knowledge, [4] is the only work providing an FTP algorithm to exactly compute an edit distance between either unordered or unlabeled trees.
The results in [4] are not explicitly given as polynomials in max{M,N}, but rather focus on the existence of a polynomial upper bound on the time complexity in terms of max{M,N}. However, they do provide an approximation of the leading coefficient for such polynomial: O(2.62k). We set ak=2.62k. We want to compare such coefficient with bk=22τ(k)τ(k)τ(k)+2≥26⋅2k+1(3⋅2k+1)3⋅2k+1+2, which is a lower bound for the leading coefficient of the algorithm in [25], assuming T=Tl. Clearly, directly comparing dI(T,G)<k and dE(T′,G′)<k, with T′ and G′ having the same tree structures as, respectively, T and G, is not fair. In fact, dI is a "sup" kind of distance, collecting only the biggest difference between trees, while dE collects all the differences between trees, which are added to obtain the final value. Thus, when computing dE, we multiply k by the number of edges in T′ and G′, i.e., we compare dI(T,G)<k with dE(T′,G′)<k(M+N). For N=M=20, and k=1,2,3,4,5, we obtain: ak∼108,1016,1025,1033,1042 while bk∼1018,1043,1098,10223,10501.
Now, we focus on [3]. The authors of the paper provide a O((M+N+2)5/2log(M+N+2)) time algorithm, to approximate dI up to a factor of O(min{M+N+2,√r⋅(M+N+2)), with r being equal to the ratio of the longest edge across T and G, over the smallest edge across T and G. More precisely, it takes O((M+N+2)2) to determine if dI(T,G)≤k up to a multiplicative factor of:
Note that c depends on T and G, and cannot be controlled or improved by changing some parameters.
Let ˜d(T,G) be the value returned by the algorithm in [3]. We know that dI(T,G)/˜d(T,G)≤c, and thus:
So, we can get a maximum range for the relative error introduced by ˜d, by taking c−1/c, similarly to what was done with Eq (10.1). We compute such error ranges across the first four datasets considered in Section 10.3 to compare them against the ones we obtained with Δ.
We obtained the following mean values for the error ranges: 35.19 ("Growth"), 30.63 ("Octane"), 39.93 ("NOx"), 35.22 ("Tecator"). We point out that this means that, on average, the error range produced by ˜d is more than 300% of ˜d(T,G). Our approach, instead, produced much more reliable estimates, as for 95% of our distances, Δ was less than 0.008. Thus, we argue that, whenever feasible, our estimation should be preferred to the techniques in [3].
C.
Computational runtimes
We now present a simulation study to showcase the computational runtimes of the implementation that was used in the case studies in Section 10. The data generating pipeline is the same as in Section 10.1, with the cardinality of the point cloud, i.e., the number of leaves in the trees, being ni=5,10,15,20,25,30,35. For each value of ni, we sample 200 couples of point clouds, and compute du betwen the associated merge trees. We report the boxplots of the obtained runtimes in Figure 15.
We close the simulation with the following disclaimer: given the nature of the present work, our focus has not been on optimizing the code or the computational environment. For instance, we used a non-commercial version of the Gurobi 12 solver, without having ample RAM dedicated exclusively to these computations. Consequently, the reported runtimes do not accurately reflect the potential efficiency of a fully optimized implementation. See state-of-the-art implementations of metrics with similar complexity, such as [31].
D.
Proofs
D.1. Proof of Proposition 1
We consider separately the different combinations arising from the considered vertices belonging to πT(C) or D.
● The thesis is obvious if x,x′∈πT(C);
● If x∈πT(C) and x′∈D, then w≥χ(x′), with (x,w)∈C. Otherwise, (C3) is violated since #Λ(x)>1, and so, αC(x)≥αC(x′);
● If x′∈πT(C) and x∈D, then χ(x)≤w with (x′,w)∈C;
● Lastly, suppose x,x′∈D and consider the following cases:
– If #Λ(x)=#Λ(x′)=0, then we have φ(x)=φ(x′), and, thus, f(x)+12(f(φ(x))−f(x))≤f(x′)+12(f(φ(x′))−f(x′)). This entails g(αC(x))≥g(αC(x′));
– If #Λ(x),#Λ(x′)>1, then we have χ(x)≤χ(x′), and the thesis clearly follows;
– Lastly, suppose that #Λ(x)=0 and #Λ(x′)=1; then, η(x)≤χ(x′).
D.2. Proof of Lemma 1
Given x∈T, if maxπT(C)∈{v∈T∣v≥x}, we have a well-defined upper extreme uC(x). Moreover, since {v∈T∣v≥x} is totally ordered, uC(x) is unique. If maxπT(C)∉{v∈T∣v≥x}, i.e., LCA(x,maxπT(C))>maxπT(C), then uC(x)=+∞.
Now, consider x∈LT. Since subT(x)={x}, then x∉U. Thus, also lC(x) is well-defined. On top of that, since by hypotheses, we are considering only vertices such that x∉πT(C)∪D, x≠lC(x)≠uC(x). Thus, [lC(x),uC(x)] is a nondegenerate sequence of edges.
Suppose {v∈U∣lC(x)≤v≤x}=∅ and v′,v″. Clearly, [v', x]\bigcap [v'', x] \bigcap V_T \neq \emptyset ; so consider p \in [v', x]\bigcap [v'', x] \bigcap V_T . We know p\notin U , thus, p \in \pi_T(C)\cup D , which is absurd since v', v'' < p .
Lastly, suppose x\in U (and so \#\Lambda(x) = 1 ) and \max \{v\leq x \mid v \in \pi_T{C}\cup D\}\subset D . Then, \#\Lambda(l_C(x))\neq 1 for any l_C(x) . Let \{v\} = \Lambda(x) and consider [v, x] . If v'\in U for all v < v' < x , we are done. Clearly, there cannot be vertices v' with v < v' < x which are in \pi_T(C) . So suppose there is v'\in D , with v < v' < x . Since v\in \Lambda(v') , we have \#\Lambda(v') > 0 , but then \#\Lambda(v') > 1 , which means v, v''\in \Lambda(v') for some v'' < v' . Clearly, in [v'', x] there can be no vertex contained in \pi_T(C) apart from v'' . Thus, \#\Lambda(x) > 1 , which is absurd.
D.3. Proof of Proposition 3
We need to check continuity. Consider x_n\rightarrow x in {\bf T} . We know that their order relationships is preserved by \alpha_C and \alpha_C^\varepsilon . On top of that, f(x_n)\rightarrow f(x) yields f(x_n)+\varepsilon\rightarrow f(x)+\varepsilon and the result follows.
D.4. Proof of Lemma 2
We know that \#\Lambda(x), \#\Lambda(y) > 1 . Thus, x, y are either deleted or coupled. Note that \chi(x)\geq y and \chi(y)\geq x . If both of them are coupled, then (x, y)\in C . Suppose x is coupled with \delta(y) and y is deleted. Then, cost(y) = \mid f(\chi(y))-g(y)\mid < \varepsilon and cost(x) = \mid f(x)-g(\delta(y))\mid < \varepsilon . Since \delta(y)\geq y and \chi(y)\geq x , we obtain the thesis.
D.5. Proof of Theorem 1
First, we check continuity, and then we check (P1)–(P3).
● \alpha_C^\varepsilon is continuous by Proposition 3.
● (P1) holds by Proposition 3.
● Now, we prove (P2). Suppose we have \alpha_C^\varepsilon(v) < \alpha_C^\varepsilon(v') and set x = {\rm{LCA}}(v, v') .
We can suppose \#\Lambda(x) > 1 and {\rm{LCA}}(\Lambda(x)) = x ; otherwise, at least one between \varphi(v)\geq x and \varphi(v')\geq x holds. Suppose the second one holds, then \#\Lambda(v') = 0 and \varepsilon\geq (f(\varphi(v'))-f(v'))/2 and \varphi(v')\geq x . Thus, (P2) holds. The same if the first one holds.
Now, we show that if \#\Lambda(x) > 1 , we can find a, b\in V_T such that:
– x = {\rm{LCA}}(a, b) ;
– (a, a'), (b, b')\in C ;
– \alpha_C(v)\geq \alpha_C(a) and \alpha_C(v')\geq \alpha_C(b) .
Note that, in this case, upon calling y = {\rm{LCA}}(a', b') , we have: \mid f(x)-g(y) \mid \leq \varepsilon by Lemma 2, \alpha^\varepsilon_C(v')\geq \{\alpha_C(v), \alpha_C(a), \alpha_C(b)\} , and so, \alpha_C(v')\geq y , which means that f(v')+\varepsilon \geq g(y) . Thus, f(x)-f(v') \leq 2\varepsilon .
We enumerate all the possible situations for v ; clearly, the same hold for v' :
– v\in \pi_T(C) : then a = v ;
– \Lambda(v) = 0 : then a = v'' with (v'', \eta(v))\in C ; by hypothesis, \varphi(v)\leq x and v'' < x ;
– if v\notin \pi_T(C) and \#\Lambda(v) > 0 : then a\in\Lambda(v) .
● Now, we prove (P3). If w \notin Im(\alpha_C^\varepsilon) , then w \in D_C^G . In fact, if (x, w')\in C with w' < w , then [w', w]\subset Im(\alpha_C^\varepsilon) , since there are l(w)\geq w' and u(w)\leq r_{G} . Then, we know that there is w'' = \min \{y\in V_G \mid y > w \text{ and }y\notin D_C^G\} with g(w'')-g(w)\leq \varepsilon .
D.6. Proof of Corollary 1
We know that w: = \alpha(v)\leq w': = \alpha(v') ; thus, \max\{y \in V_G \mid y\geq w\}\leq \max\{y \in V_G \mid y\geq w'\} , and the thesis follows.
D.7. Proof of Theorem 2
We build C by subsequently adding couples starting from an empty set. The proof is divided in sections which should help the reader in following the various steps.
Before starting, following [25], we can take \beta:{\bf G}\rightarrow {\bf T} induced by \alpha so that \alpha and \beta are \varepsilon -compatible.
Step 1. Leaves of T
Step 1.1. Selecting the coupled leaves
We consider the following set of leaves:
We give a name to the condition:
(a) \nexists v'\in L_T \text{ such that }\alpha(v) < \alpha(v'),
so that we can more easily use it during the proof. Note that we can avoid treating the case \alpha(v) = \alpha(v') thanks to (G) .
The set \mathcal{L}_T is the set of leaves which will be coupled by C , while all other leaves will be deleted: we add to C all the couples of the form (v, \phi(v)) with v\in \mathcal{L}_T . We characterize those couples with the following proposition.
Lemma 5. Given v, v'\in \mathcal{L}_T , then \phi(v)\geq \phi(v') if and only if v = v' . Moreover, for every v'\in L_T such that (a) does not hold, there is v\in\mathcal{L}_T such that \alpha(v) < \alpha(v') .
Proof. The first part of the proof reduces to observing that \phi(v)\leq \phi(v') if, and only if, \alpha(v)\leq \alpha(v') .
Now, consider v'\in L_T such that (a) does not hold. We know there is v_0 such that \alpha(v_0) < \alpha(v') . If v_0\in\mathcal{L}_T , we are done; otherwise, there is v_1 such that \alpha(v_1) < \alpha(v_0) < \alpha(v') . Note that f(v_1) < f(v_0) . Thus, we can carry on this procedure until we find v_i\in \mathcal{L}_T . Note that \arg\min_{V_T} f \in \mathcal{L}_T ; thus, in a finite number of steps, we are done. □
Step 1.2. Cost bound on couples
Now, we want to prove the following proposition, which gives an upper bound for the cost of the couples added to C .
Lemma 6. Given v\in \mathcal{L}_T , then \mid f(v)-g(\phi(v))\mid \leq \varepsilon .
Proof. Suppose the thesis does not hold. Since g(\phi(v))\leq f(v)+\varepsilon , contradicting the thesis means that we have v\in\mathcal{L}_T such that:
(b) g(\phi(v))+\varepsilon < f(v) .
Let w = \phi(v) . If (b) holds, then g(father(w))-g(w) > g(\alpha(v))-g(w) > 2\varepsilon . Let v' = \psi(w)\leq \beta(w) . Note that f(v') < f(v) . We have \phi(v')\leq \alpha(v')\leq \alpha(\beta(w)) = s^{2\varepsilon}_G(w) . Since g(father(w))-g(w) > 2\varepsilon , we also have \alpha(v')\leq \alpha(v) with v'\neq v , which is absurd by Lemma 5. □
Step 1.3. Cost bound on deletions
In this step, we prove the following proposition which gives an analogous bound to the one of Lemma 6, but for the deleted leaves of T .
Lemma 7. Given v\in L_T-\mathcal{L}_T , then there exists x > v such that:
● There is v' < x such that v'\in \mathcal{L}_T ;
● f(x)\leq f(v)+2\varepsilon .
Proof. Since (a) does not hold for v , we use Lemma 5 to obtain v'\in \mathcal{L}_T such that \alpha(v') < \alpha(v) . However, since \alpha is an \varepsilon -good map, we have s_T^{2\varepsilon}(v')\leq s_T^{2\varepsilon}(v) which implies f({\rm{LCA}}(v, v'))\leq f(v)+2\varepsilon . Thus, x = {\rm{LCA}}(v, v') ends the proof. □
Lemma 7 implies that, using the notation of the proposition, \varphi(v)\leq x . Then, f(v) < f(v') implies that g(\phi(v))\leq f(v')+\varepsilon < f(v)+\varepsilon . Thus, g(\eta(v)) < f(v)+\varepsilon . Since f(x)\leq f(v)+2\varepsilon , we have that the cost of deleting any x' < x with \#\Lambda(x') = 0 is less then \varepsilon .
Step 2. Leaves of G
Lemma 8. Given w\in L_G , there exists y\geq w such that:
● There is w' = \phi(v) with v\in\mathcal{L}_T and w' < y ;
● g(y)\leq g(w)+2\varepsilon .
Proof. Consider \beta(w) . Let v\leq \beta(w) leaf. We have \alpha(\beta(w))\geq {\rm{LCA}}(\alpha(v), w) . If v\in\mathcal{L}_T we are done for \phi(v)\leq \alpha(v) . If (a) does not hold by Lemma 5, it means that there is v'\in \mathcal{L}_T such that \alpha(v') < \alpha(v) . We are done since g(\alpha(\beta(w))) = g(w)+2\varepsilon . □
Note that if w < \phi(v) for some v\in\mathcal{L}_T , then, by Lemma 8, g(\phi(v))\leq g(w)+2\varepsilon . In fact, using the notation of Lemma 8, in this case, we have w' = y = \phi(v) by definition. As in Step 1.3, we have that the cost of the deletion of any w such that \#\Lambda(w) = 0 and w\notin \pi_G(C) is at most \varepsilon .
Step 3. Internal vertices
Now, we need to extend the coupling C taking into account the internal vertices of T . We will do so after simplifying our merge trees in two different ways: First, we remove all vertices which are deleted with \#\Lambda(p) = 0 , and then we take out all inessential internal vertices.
Step 3.1. Pruning
Let T_0 = T and G_0 = G . We define T_1 as the merge tree obtained from T_0 deleting the following set of vertices (and the corresponding edges): x satisfying both \#\Lambda(x) = 0 and x\notin \pi_T(C) . Note that, for any x\in V_T , either there is v\leq x with v\in\mathcal{L}_T or, for any leaf below x , we can apply Lemma 7 and the consequential observations.
The tree G_1 is obtained from G_0 in an analogous way: any time we have w\in V_G satisfying both \#\Lambda(w) = 0 and w\notin \pi_G(C) , w is deleted from G_0 , along with the edge (w, father(w)) .
Before proceeding, we point out that, by construction, the leaves of T_1 are exactly \mathcal{L}_T .
Step 3.2. Restricting \alpha
Thanks to Corollary 1, we have that anytime we delete some vertex in G_0 to obtain G_1 and that vertex is in the image of \phi , we are sure that also its counterimage is deleted from T_0 .
Now, for every v\in{\bf T} , by construction we have that \alpha(v) belongs to an edge removed from G_0 if, and only if, \phi(v) is deleted from G_0 . Consider v' = \ell(v)\in V_T . Then, \phi(v')\leq \phi(v) , and thus, \phi(v') is deleted as well. This entails that v' is deleted as well. All of this put together implies that we can restrict \alpha to {\bf T}_1 (the metric tree obtained from T_1 ), and its image lies in {\bf G}_1 (obtained from G_1 ).
Step 3.3. \varepsilon -Good restriction
We define \alpha_1: = \alpha_{\mid {\bf T}_1}:{\bf T}_1\rightarrow {\bf G}_1 . We want to prove that \alpha_1 is still an \varepsilon -good map. Clearly, (P1) and (P2) still hold upon restricting the domain. We just need to show (P3) . Suppose there is w\in V_{G_0} such that w\notin \alpha_1({\bf T}_1) . We distinguish between two cases: (1) w\notin \phi({\bf T}_1) and (2) w\in \phi({\bf T}_1) . Consider scenario (1) : w\notin \phi({\bf T}_1) clearly implies that \#\Lambda(w) = 0 , and so, w is deleted; scenario (2) instead means that there is \alpha(v) = \min \{\alpha(v') > w\mid v'\in{\bf T}_1\} with \ell(\alpha(v)) = \phi(v) = \ell(w) . Clearly, \{w' \in {\bf G}_0\mid w' < w \}\bigcap \alpha({\bf T}_1) = \emptyset , and, thus, v is a leaf of T_1 , which means v\in\mathcal{L}_T . This also implies that w\notin \alpha({\bf T}) , and, in particular, \alpha(v) = \min \{\alpha(v') > w\mid v'\in{\bf T}_0\} , thus condition (P3) is satisfied.
Step 3.4. Properties of \phi:{\bf T}_1\rightarrow {\bf G}_1 and removal of inessential vertices
We know that \phi:L_{T_1}\rightarrow L_{G_1} is injective. On top of that, we have proved that, if w\notin \alpha_1({\bf T}_1) , then \ell(w) = \phi(v) for some v\in\mathcal{L}_T . Thus, \phi:L_{T_1}\rightarrow L_{G_1} is a bijection.
From now on we will ignore any vertex v such that \#child(v) = 1 . Formally, we introduce T_2 (and G_2 ) obtained from T_1 ( G_1 ) removing all the vertices v\in V_{T_1} such that \#child(v) = 1 , (similarly, w\in V_{G_1} such that \#child(w) = 1 ): consider \{v'\} = child(v) . We remove v from V_{T_1} and replace the edges (v', v) and (v, father(v)) with the edge (v', father(v)) . We do this operation recursively until no vertices such that \#child(v) = 1 can be found.
Step 3.5: Coupling and deleting internal vertices
We start with the following lemma:
Lemma 9. For every x\in V_{T_2} , and y\in V_{G_2} , we have \mid x-\chi(x)\mid \leq \varepsilon and \mid y-\chi(y)\mid \leq \varepsilon .
Proof. Let x\in V_{T_2}-L_{T_2} . Then, x = {\rm{LCA}}(v_1, \ldots, v_n) with v_1, \ldots, v_n being the leaves of sub_{T_2}(x) . Then, \alpha(x) > \alpha(v_i) for every i , and, thus, \alpha(x)\leq w = \chi(x) = {\rm{LCA}}(\alpha(v_1), \ldots, \alpha(v_n)) . Clearly, x\leq \beta(w) for analogous reasons. Thus, \mid x-w\mid\leq \varepsilon . For y\in V_{G_2} , we can make an analogous proof. □
Let v_1, \ldots, v_n\in L_{T_2} and \phi(v_1), \ldots, \phi(v_n)\in L_{G_2} . Let x = {\rm{LCA}}(v_1, \ldots, v_n) and y = {\rm{LCA}}(\phi(v_1), \ldots, \phi(v_n)) . We know that \alpha(x)\geq y and \beta(y)\geq x , and so \mid f(x)-g(y)\mid \leq \varepsilon .
Thus, we proceed as follows: we order all the internal vertices of T_2 according to their height values and we start from the higher one (the root of T_2 ; note that this, in general, is not the root of T_0 ), coupling it with the other root (thus, (C1) is verified). Consider a lower x , and let v_1, \ldots, v_n be the leaves of sub_{T_2}(x) , (and, thus, x = {\rm{LCA}}(v_1, \ldots, v_n) ). Let w = {\rm{LCA}}(\phi(v_1), \ldots, \phi(v_n)) . If the leaves of sub_{G_2}(w) are \phi(v_1), \ldots, \phi(v_n) , we add the couple (x, w) , otherwise, we skip x which will be deleted, with \#\Lambda(x) > 1 . Note that w = \chi(x) . Moreover, by Lemma 9, \mid f(x)-g(w)\mid \leq \varepsilon . Going from the root downward we repeat this procedure for every x .
We clearly have:
● (C3) is satisfied;
● cost((v, w))\leq \varepsilon ;
● If v\in V_{T_2} is deleted, then \#\Lambda(v) > 1 and cost(v) = \mid f(v)-g(\chi(v))\mid \leq \varepsilon ;
● If w\in V_{G_2} is deleted, then \#\Lambda(w) > 1 and cost(w) = \mid g(w)-f(\chi(w))\mid \leq \varepsilon by Lemma 9.
Step 4. Coupling Properties and Costs
First, we verify that C is a coupling:
(C1) See Step 3.5;
(C2) See Step 1 and Step 3.5, we carefully designed the coupling so that no vertex is coupled two times;
(C3) It is explicitly proven in Step 3.5;
(C4) In Step 3.4, we remove all vertices such that \#child(x) = 1 to obtain T_2 and G_2 ; all the couples in C are either leaves of vertices in T_2 and G_2 . So, since all leaves of T_2 and G_2 are coupled, its impossible to have a vertex p belonging to any tree such that \#\Lambda(p) = 1 .
Lastly, we verify its costs:
● If (x, y)\in C , then \mid f(x)-g(y)\mid \leq \varepsilon as verified in Step 1.2 for x\in L_T , and in Step 3.5 for x being an internal vertex;
● If x \in V_T\cap D , with \#\Lambda(x) = 0 , it is verified that \mid f(x)-\phi(x)\mid \leq 2 \varepsilon in Step 1.3; if instead y\in V_G\cap D , we verify \mid g(y)-\phi(y)\mid \leq 2\varepsilon in Step 2; in both cases, we have a vertex lower than x (y) which, by construction, is coupled, and the cost of the couple is less then \varepsilon . Thus, the deletion of x (y) costs less than or equal to \varepsilon ;
● If p \in D , with \#\Lambda(p) > 1 , then we verify in Step 3.5 that the cost of this deletion is less than or equal to \varepsilon .
This concludes the proof.
D.8. Proof of Theorem 3
First, we prove the second part of the statement.
Given C\in \mathcal{C}(T, G) optimal coupling such that \{(r, r')\} = \max C , we define \mathcal{M}(C): = \max (C- \{(r, r')\}) . Clearly, \mathcal{M}(C)\in \mathcal{C}^*(T, G) . For any (x, y)\in \mathcal{M}(C) , consider C^o_{x, y}\in \mathcal{C}_R^o(T_x, G_y) such that \parallel C^o_{x, y}\parallel_\infty \leq \parallel C_{\mid (x, y)}\parallel_\infty with C_{\mid (x, y)}: = \{(v, w)\in C \mid (v, w) < (x, y)\} . By hypothesis, we know that C^o_{x, y} exists for every x, y . Note that C_{\mid (x, y)}\in\mathcal{C}_R(T_x, G_y) .
We want to prove that the extension C': = \{(r, r')\}\cup (\bigcup_{(x, y)\in \mathcal{M}(C)} C^{o}_{x, y}) satisfies \parallel C'\parallel_\infty \leq \parallel C\parallel_\infty . The set C' clearly is a coupling since for every x, x'\in\pi_T(\mathcal{M}(C)) , sub_T(x) and sub_T(x') are disjoint, and the same for y, y'\in\pi_G(\mathcal{M}(C)) . We need to consider the costs of different kinds of vertices separately. In particular, we indicate with (a) whenever we have v\in V_T such that v\leq x for some x\in \pi_T(\mathcal{M}(C)) . If this condition does not hold, we say that (b) holds for v . The same definitions apply also for vertices in G . For instance, (a) holds for all vertices in \pi_T(\mathcal{M}(C)) and \pi_G(\mathcal{M}(C)) . Similarly, if (b) holds for v , then it holds also for all v' > v .
● Consider v\in V_T such that (a) holds for some (x, y)\in \mathcal{M}(C) ; we have that \chi_{C'}(v)\leq y , \varphi_{C'}(v)\leq x and \eta_{C'}(v)\leq y , so cost(v) depends only on C^o_{(x, y)} . Thus, by construction, cost_{C'}(v) = cost_{C^o_{(x, y)}}(v)\leq \parallel C_{\mid(x, y)}\parallel ;
● Suppose now (b) holds for v\in V_T ; by construction, in this case, we have \chi_C(v) = \chi_{C'}(v) , \Lambda_{C'}(v) = \Lambda_{C}(v) , and, thus, \varphi_C(v) = \varphi_{C'}(v) . Suppose \Lambda_{C'}(v) = 0 : (a) holds for \eta_{C'}(v) by means of some y\in\pi_G(\mathcal{C}(M)) , and, thus, g(\eta_{C'}(v)) = \min_{w'\leq y}g(w')\leq g(\eta_{C}(v)) (thanks to the properties of couplings in \mathcal{C}^o_R(T_x, G_y) ). Since \varphi_C(v) = \varphi_{C'}(v) , we then have cost_{C'}(v)\leq cost_C(v) . Lastly, consider \#\Lambda_{C'}(v) > 1 . In this case, we have \chi_{C}(v) = \chi_{C'}(v) = r' , and, thus, cost_{C'}(v) = cost_C(v) . Note that in all these situations, cost_{C'}(v) does not depend on the chosen extension.
Exchanging the role of T and G , we obtain the same results for the vertices of G .
The first part of the statement follows with analogous reasoning, by dropping the special coupling constraints and focusing on the vertices v \in \pi_T(e(C^*))\text{ or } \#\Lambda_{e(C^*)}(v) > 0 . In particular, the special couplings constraints are necessary only if \#\Lambda_{e(C^*)}(v) = 0 .
D.9. Proof of Lemma 3
1) This is due to the fact that all vertices of P\varepsilon(T) are coupled, and, thus, P\varepsilon(T) is still a rooted tree and (P) does not alter the order relationships of the remaining vertices;
2) Since (P) removes at most one leaf from the previous tree and adds no new leaves, it is clear that L_{P_\varepsilon(T)}\subset L_T . Consider now v\in L_T . Define:
Note that both vertices are well-defined and (v_-, v_+)\in E_T .
Let v' = \arg\min_{v''\leq v_+} f(v'') . We show that v' can't be deleted by the recursive application of (P), which also implies the thesis. Suppose it is deleted.
By construction, v' is the last leaf, in terms of recursive applications of (P) and among the leaves below v_- , that are deleted. In fact, at any step along the recursion, any sibling v'' of v' will always have a lower distance to the common father. Thus, v' cannot be deleted until it has siblings, i.e., all other leaves below v_- are deleted as well. This also means that, at some point along the recursion, v_- becomes the father of v' . After all the siblings of v' are removed from the tree, finally, v_- becomes a degree 2 vertex with v' as an only child, and it is removed as well. So, v_+ becomes the father of v' . At this point we have:
which is absurd as, for v' to be deleted, we must have f(father(v'))-f(v') < \varepsilon ;
{\rm{i}}) Consider v\in V_T- V_{P_\varepsilon(T)} ; let \Lambda_{C_\varepsilon}(v) = \{a_1, \ldots, a_n\} . By construction, v\geq x = {\rm{LCA}}(\Lambda_{C_\varepsilon}(v)) . We know that a vertex is removed from T if, at a certain point along the recursive application of (P) , it becomes a degree 2 vertex or a small-weight leaf. Thus, the vertex x is not removed from T unless n\leq 1 , which is absurd because then \Lambda_{C_\varepsilon}(v) = \{x\} . Thus, \#\Lambda(v)\leq 1 . As a consequence, v\in D if, and only if, \#\Lambda(v) = 0 .
The vertex \varphi_{C_\varepsilon}(v) is the first vertex x above v such that there is a leaf v' , v' < x , with f(x)-f(v')\geq \varepsilon . If f(x)-f(v)\geq \varepsilon , then by point (2) there exist v'\in L_{P_\varepsilon(T)} with {\rm{LCA}}(v', v) < \varphi_{C_\varepsilon}(v) which is absurd;
{\rm{ii}}) Consider two leaves v, v'\in L_T with f(v) < f(v') , with v\notin V_{P_\varepsilon(T)} and v'\in V_{P_\varepsilon(T)} . On top of that, suppose v' < \varphi_{C_\varepsilon}(v) . By point (3) we have f(\varphi_{C_\varepsilon}(v))-f(v') < \varepsilon which means that v' is a small-weight leaf, which is absurd;
{\rm{iii}}) Combining points (3) and (4), we see that we only have deletions with \#\Lambda_{C_\varepsilon}(v) = 0 and 2\cdot cost_{C_\varepsilon}(c) = f(\varphi_{C_\varepsilon}(v))-f(v)\leq \varepsilon .
D.10. Proof of Proposition 4
Consider C\in\mathcal{C}(P_\varepsilon(T), P_\varepsilon(G)) . Then, C can be seen also as a coupling C\in\mathcal{C}(T, G) . Let C_\varepsilon be as in Lemma 3.
We partition the vertices V_T into three sets:
● The case v\in V_{P_\varepsilon(T)} is not a concern since the cost doesn't change when considering v\in V_T or v\in V_{P_\varepsilon(T)} ;
● If v \in U^T_{C_\varepsilon} , then v \in U^T_C or v\in D^T_C . We ignore the first case. In the second case, \{v'\} = \max\{v'' < v\mid v''\in V_{P_\varepsilon(T)}\} , is such that v'\in D_C^T , and so cost_C(v) < cost_{C}(v') ;
● If v\in D^T_{C_\varepsilon} , then v\in D^T_{C} and \#\Lambda_C(v) = 0 ; by construction \varphi_{C_\varepsilon}(v)\leq \varphi_{C}(v) . If \varphi_{C_\varepsilon}(v) < \varphi_{C}(v) , then also \eta_{C_\varepsilon} is deleted and, since f(\eta_{C_\varepsilon}(v)) < f(v) , cost_C(v) < cost_C(\eta_{C_\varepsilon}(v)) .
So, we are left with the case \varphi_{C_\varepsilon}(v) = \varphi_{C}(v) . If g(\eta_C(v))-f(v) > 0.5\cdot \left(f(\varphi_{C}(v)-f(v))\right) , then, again, cost_C(v) < cost_C(\eta_{C_\varepsilon}(v)) , for f(\eta_{C_\varepsilon}(v)) < f(v) . Thus, we always have cost_C(v)\leq \max\{\varepsilon/2, cost_C(\eta_{C_\varepsilon}(v))\} .
Exchanging the role of T and G , and repeating the same observations, we obtain that, if we consider C\in\mathcal{C}^{o}(T, G) , we have d_I(T, G)\leq \parallel C \parallel_\infty\leq \max\{d_I(P_\varepsilon(T), P_\varepsilon(G)), \varepsilon/2\} .
D.11. Proof of Lemma 4
● If v\leq r , then r'\geq \chi(v), \varphi(v) and r'\geq \eta(v) , so cost(v) depends only on C_{r, r'} ;
● If v\nleq r , then it is either unused, if v > r , or it is deleted with \#\Lambda(v) = 0 . Then the cost of such deletion is either 0.5(f(v_r)-f(v)) or g(\eta(v))-f(v) . If C_{r, r'}\in\mathcal{C}^o_R(T_r, G_{r'}) , g(\eta(v)) = g_r , and so we are done. Otherwise, we simply have g(\eta(v))\geq g_r , and, thus, g(\eta(v))-f(v)\geq g_r-f(v) implying the lower bound that we needed to prove.
D.12. Proof of Proposition 5
We just explore the different pieces of the cost function to assess the thesis:
● In the case of (x, y)\in C_\mathcal{V} , the cost of coupling T_x and G_y is given by \sum_{y} a_{x, y}\parallel C_{x, y}\parallel _\infty ;
● If u_x = 1 , we have \mid g(r_G)-f(x)\mid u_x which is the cost of deleting x with \#\Lambda(x) > 1 . That is, any time x\geq x' with x' = {\rm{LCA}}(v, v') for v, v'\in \pi_T(C_\mathcal{V}) . Recall that, in this case, we have \chi(x)\leq r_G ;
● Deleting x with \#\Lambda(x) = 0 is taken care by the remaining part the cost function. For a vertex x , we indicate with x_f its father, and set A_x = 0.5(f(x_f)-f_x)(1-d_x) and B_x = \lbrace \sum_y a_{v, y}\left(g_y-f_x \right) - K d_x \rbrace_{v\in E_T, v < x_f} . Now, we try to unveil the meaning of A_x and B_x . Recall that deleting x with \#\Lambda(x) = 0 corresponds to having d_x = 0 . If d_x = 1 , then A_x = 0 and \max B_x < 0 ; while if d_x > 1 , both A_x and \max B_x are negative. Consider now d_x = 0 . Then, \varphi_{C_m}(x) = x'_f , with x'_f being father of some x'\geq x . Clearly, d_{x'} = 0 as well and A_{x'} > A_x . In particular, A_{x'} = \max_{v\leq x'} 0.5 \left(f(\varphi_{C_m}(v))-f_v\right) (the same holds for C^o ). Now, we turn to B_x . If x < x' , then x_f < \varphi_{C^o}(x) = x'_f , and so d_{x_f} = 0 , entailing \max B_x = \min B_x = 0 . Instead, if x = x' , we have by construction v < x'_f with a_{v, y} = 1 . Then, \max \lbrace\sum_y a_{v, y} g_y\mid v < x_f \rbrace\geq g(\eta_{C^o}(x')) and so:
D.13. Proof of Corollary 3
Given C^*\in\mathcal{C}^*(T, G) , with r = {\rm{LCA}}(\pi_T(C^*)) and r' = {\rm{LCA}}(\pi_G(C^*)) , thanks to Corollary 2, we can approximate with \Gamma^\uparrow and \Gamma^\downarrow the costs of the vertices in T_r and T_{r'} . By Lemma 4, H_{r, r'} then takes care of the vertices v\nleq r and w\nleq r' .
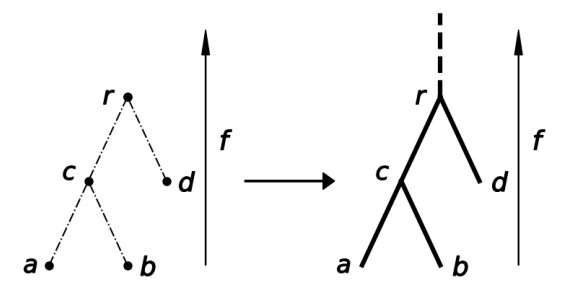









 DownLoad:
DownLoad:


















