1.
Introduction
Due to an increase in longevity of life osteoporotic fractures are becoming a major cause of morbidity, disability and mortality in elderly people. At least 200 million people worldwide is suffering from osteoporosis (OP). OP is known as silent disease. It makes bone weak and brittle over the period which results in increased susceptibility to fractures [1],[2]. This disease develops due to enhanced activity of osteoclastic cells over osteoblastic cells resulting in low bone mass. The speed of bone mass loss increases in menopause women as age advances. Between 60 to 69-year age women losses 0.6%, 70 to 79 years of age 1.1% and >80 years age groups 2.1% of bone mass per year [3].
It has been estimated that chances to have a fracture (partial or complete discontinuity in bony tissue) in later years of life is higher in women that is 40–45% as compared to 15–27% in men [4]. Whereas subsequent fractures chances are same in both genders after an initial fracture, this indicates prevention of secondary fractures are important [5],[6].
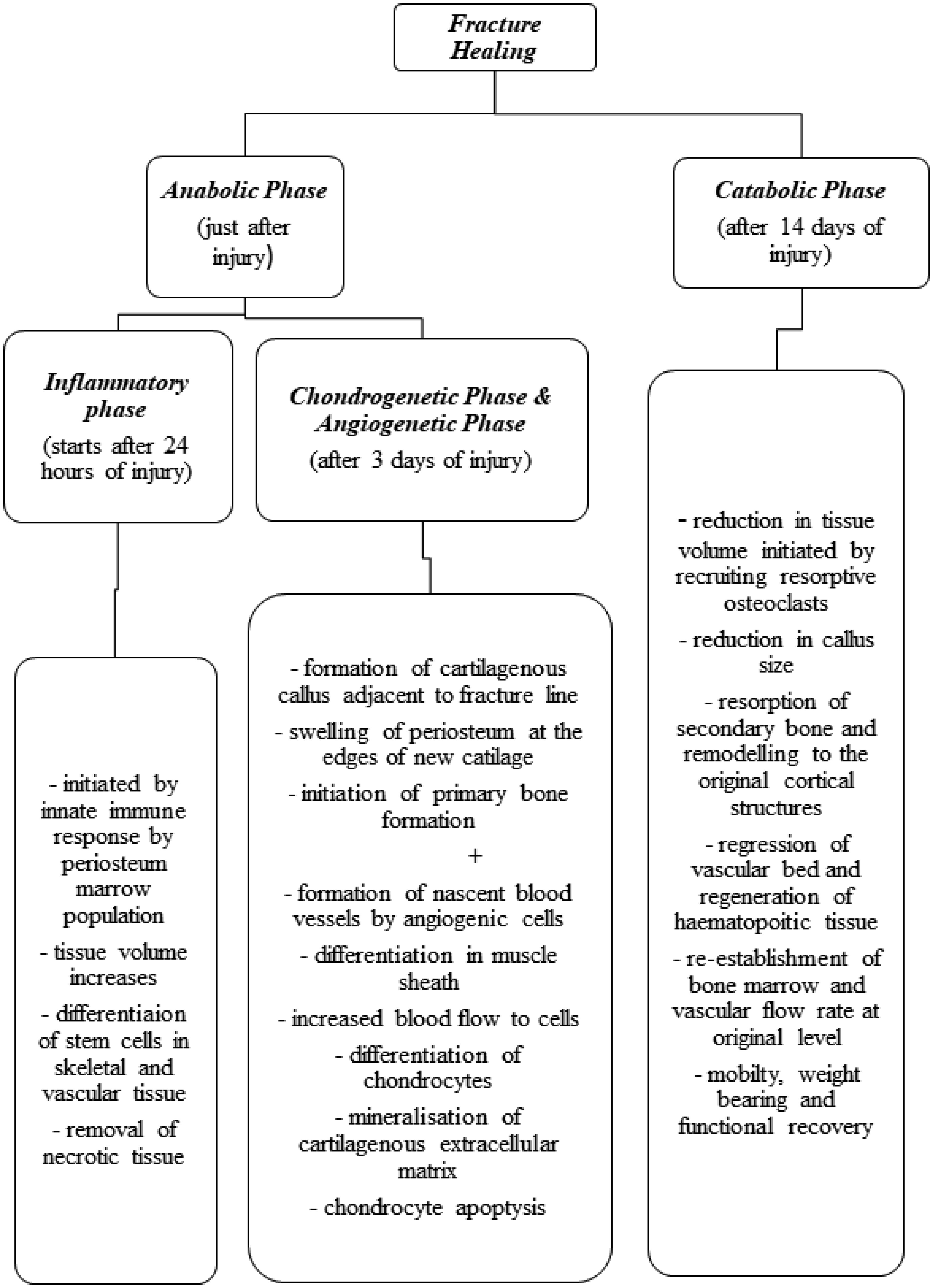
The repair of fractured bone is a postnatal regenerative osteogenesis process like ontological events of embryonic skeletal development [7]–[11]. The process of fracture healing is summarized in Figure 1.
Age is a major risk factor in case for osteoporotic fractures, as longevity of life has increased as compared to past. As a person reaches at the age of 60 years or above chances of the fragility fractures increase roughly 90% [12]. Some of the factors which predispose risk of osteoporosis are listed in Table 1.
Few extrinsic and intrinsic factors also contribute in delaying fracture healing and regeneration process. Smoking, low body weight and excess alcohol are such extrinsic whereas menopause, vitamin D deficiency, prolonged immobilization, and low calcium are such intrinsic factors [13].
As there is no such method to measure the bone mass directly, WHO has approved the bone mineral density (BMD) to predict fracture risk [14]. It has standardized the values for BMD in terms of T-scores, standard deviations as per the young adult's mean as given in Table 2.
The T-score is a division value of standard deviation of the difference between patient's BMD and young normal BMD by the standard deviation of the young normal population. It is a score whose mean is zero and variance is one. Hence, the T-score measures the standard deviation around mean BMD of young normal population. The gravity of osteoporosis increases as the T-score decreases. The OP patients will always lie on left side of the distribution and its gravity increases with increased distance towards left from centre of the distribution for T-scores. It permits the diagnosis of OP before the fracture occurs. The diagnosis of OP is with cut point set for T = −2.5 or less. The World Health Organization has recommended T-score values for OP in advance of fracture incidence. Normal T-score lies between −1 and +1. The patients with low BMD will have T-score between −2.5 and −1.0 while the patients with danger of fractures will have T-score below −2.5 [15].
Secondary OP could be gluco-corticoid induced osteoporosis (GIOP). The gluco-corticoids decrease osteoblast differentiation and increase osteoclastogenesis which results in disruption of normal bone architecture. BMD alone is not sufficient to assess internal bone structure thus the fracture risk in GIOP. Femoral neck, vertebrae, distal region of radius, pelvis, femur shaft are most common fracture sites under OP. A Fracture Risk Assessment Score (FRAX) [16],[17] is in use for assessing risk of fracture in OP. This score includes parameters like age, history of fall or previous fracture, usage of glucocorticoids along with medical conditions like diabetes, smoking, rheumatoid arthritis and alcohol consumption [18]–[20].
The most common site for osteoporotic fractures is hip, there after spine and distal forearm which impairs the quality of life of the affected patients [13]. Based on prevalence of OP in modern society due to lifestyle changes, risk of dying is same in both 50-year-old women having hip fracture due to OP or a breast cancer [21].
Surgical treatment is an elective intervention in some fractures (such as hip fracture), but a delay in such fracture repair is common which complicate the problem further [22],[23].
Although the prevention of fracture is certainly the goal in OP, an accelerated and uneventful healing process is certainly desirable. Knowing the chances of delayed and non-union it is important to review the different interventions available today for fracture healing in osteoporotic patients.
Current treatment plans and approaches in OP are majorly focused on pharmacological interventions and screenings. However, non-pharmacological options like physical exercises and other therapeutic devices cannot be overlooked and these can be quite important in preventing OP or promoting fracture healing in OP patients. Recent studies on fracture healing process revealed several molecular pathways those can trigger new bone formation, could be beneficial in treating OP and impaired fracture healing.
As each elderly patient needs unique interventions due to co-morbidities hence which treatment plan is the best treatment for the healing of fractures in osteoporotic elderly patients is still debatable. This review aims to find out currently available as well as future approaches those could be beneficial in faster recoveries. Most of the previous reviews on OP, its prevention and fracture repair have covered some specific gender, drug, physical stimulus, nutrition, bio-molecule in isolation or combination of a few while this article covers majority of the possible preventive, therapeutic, rehabilitation and pain management regimes comprehensively and emphasizes on type of research required on drugs (bisphophonates, hormonal analogues), bio-molecules (human monoclonal antibodies, sclerostin and bone morphogenic proteins), physical stimuli (electromagnetic and ultrasonic) and post-surgical rehabilitation (physical, behavioural and pain management) protocols through well designed experiments covering large number and different category of patients to fill the information gap on mechanism of action of therapies and comfort of patients.
2.
Pharmacological interventions
The pharmacological interventions reducing OP can be grouped into anti-resorptive agents that decrease bone resorption by inhibiting osteoclast activity and the anabolic agents that increase bone formation by promoting osteoblast activity. These agents also play a great role in fracture healing. Besides these pharmacological agents there are other bio-molecules which enhance fracture healing through improvement in biological environment and biomechanical functioning. Each of such intervention is reviewed as under:
2.1. Antiresorptive therapy
A systemic search conducted across the Cochrane, Google Scholar and PubMed revealed that the most popular anti-resorptive osteoporotic medications used for prevention and treatments of OP are bisphosphonates (BPs), denosumab and selective estrogen receptor modulators (SERMs).
2.1.1. Bisphosphonate
Bisphosphonates (BPs) are widely used in the treatment of OP as it reduces bone resorption by inhibiting osteoclast cell activity [24]. BPs attach hydroxyapatite binding sites on osteoclast cells surface undergoing bone resorption thus reduces bone remodelling [25]. Inhibitory effects of BPs on bone remodelling process create hinderance in fracture healing in osteoporotic fractures later on affect functional recovery after fractures [26]. A specific group of BPs (alendronate, risedronate, ibandronate and zoledronic acid) containing nitrogen have fond to be positively affecting the BMD in osteoporotic women after menopause [27],[28]. A review of trials published between 2005 and 2019 confirmed that usage of these nitrogen containing BPs was helpful in preventing the vertebral fracture compared with placebo [29],[30]. Specifically, three BPs alendronate, risedronate and zoledronic acid were effective in reducing the chances of having hip and non-vertebral fractures [29],[31].
Several studies on animals also reported same BPs effects on bone, as they are helpful in new callus formation and reduction in time taken in radius fracture healing [32]. These are also helpful in increasing BMD whereas inhibits bone remodelling process which requires for modulation of callus morphology [33]. In addition to that BPs bolus therapy for 2 weeks after hip surgery was found helpful in increasing BMD and reducing overall mortality significantly [34].
Recently, a randomized placebo-controlled trial (RPCT) study in United Kingdom published in 2019, conducted at multiple centres has found that weekly alendronate therapy at the rate of 70 mg within 14 days immediately after distal radius fracture healing does not affect adversely the fracture union or any clinical outcome treated either surgically or conservatively [35]. Another study reported contrary results on BPs administration and found increased risk of delayed union at 3 months in surgically treated inter-trochanteric fractures patients [36].
It has been established that while treating fractures in osteoporotic patients BPs increase callus volume, bone mineralization and bone-implant contact after surgery during primary endochondral phase but delays remodelling of callus and healing rate [37]–[40].
2.1.2. Denosumab
Denosumab is a potent mediator of bone resorption as it is an inhibitor of osteoclast thus at fracture site it increases callus volume but delays remodelling [41]. Studies on animals have revealed that after binding with RANKL (Receptor Activator of Nuclear Factor “kappa light chain enhancer” of activated B-cells Ligand) denosumab prevents RANKL to bind its receptor site on cellular surface which is essential for osteoclast differentiation and delayed remodelling even with better biomechanical properties [42]. However, no significant delay in fracture healing was noticed due to denosumab in patients previously receiving antiresorptive therapy for osteoporosis [43]. It is suggested that clinical studies on the effect of denosumab are clinically inconclusive regarding its effects on delayed or non-union or any kind of impaired fracture healing. Therefore, it warrants further studies for their use in humans.
Hanley et al. [44] clearly explained the mechanism of action of Denosumab, molecular pathways and targets of anabolic and antiresorptive treatment through figures. The denosumab binds with RANKL and prevents it to activate its receptor RANK on surface of osteoclast thereby inhibits osteoclastogenesis and does not decrease bone mass [45] which makes it a first choice of treatment to prevent vertebral, non-vertebral and hip fractures [46]. The bisphonates get embedded in bone tissue and binds the bone matrix. Such binding strength and period of action are highest for zolendric acid followed by alendronate and risedronate in descending order [47]. On the other hand, denosumab does not get embedded in bone tissue and as a human monoclonal antibody it binds RANKL causing dramatic decline in, the bone resorption marker CTX (a fragment of bone collagen protein) after single dose of 60 mg denosumab. Since this effect is reversible hence for re-initiation of this process the treatment is repeated after 9 months [48]. Superiority of twice a year dosing of denosumab over alendronate in increasing cortical BMD and its microarchitecture was established after long-term studies for 2–3 years [49].
Very recently in June 2019 a recent systemic review and meta-analysis was conducted by Fang et al. [50] after identifying 1423 records through data base search (1266 records on denosumab and 157 on romosozumab) amongst which 260 (225 on denosumab and 35 on romosozumab) were full text articles in English, and only 17 (11 on denosumab and 6 on romosozumab) were randomized clinical trials qualifying the criteria for conducting meta-analysis. They concluded that 12–36 months of therapy by denosumab or romosozumab in osteoporotic patients does not increase the composite as well as specific cardiovascular (CV) outcomes. In composite outcome 3 P MACE (three-point major cardiovascular events) that is CV death, myocardial infarction, and stroke comes where as in specific CV outcomes atrial fibrillation, heart failure, aortic and intracranial aneurism, aortic dissection, aortic valve disease and serious hypertension comes. However, risk of 4 P MACE (four-point major cardiovascular events, including 3 P MACE and heart failure) may increase after romosozumab therapy.
2.1.3. Selective Estrogen Receptor Modulator
Two types of estrogens receptors (ER) ERα and ERβ have been identified on the osteoblasts, osteoclasts, osteocytes and bone marrow stromal cells [51]. These Selective Estrogen Receptor Modulators (SERMs) are a class of compound that interact specifically through the binding and activation of these intracellular ERs without affecting other organs in the body [52],[53].
The two main chemical classes of SERM are approved for clinical use. First one Teriphenylethylene derivative which are used to treat breast cancer and were derived from Tamoxifen and Toremifene. Other one is Benzothiopene derivative, Raloxifene, which indicated for the treatment and prevention of OP [53]–[57]. The action of SERMs on the estrogen receptor affects bone homeostasis by reducing the activity of osteoclasts and reducing bone resorption. In different clinical trials [58]–[60] 60 mg/day of raloxifene was found effective in prevention and treatment of postmenopausal OP.
A randomized clinical trial was conducted by Ettinger B et al. [60] on postmenopausal women who met WHO criteria for having OP. Participants were divided randomly in three groups: first group received 60 mg raloxifene per day, second group received 120 mg raloxifene per day and the third group received placebo pills. Calcium and cholecalciferol supplementation were given to patients in all the groups along with the specific treatment. It was concluded that raloxifene increased bone mineral density in the spine and femoral neck after assessing it with dual X-ray absorptiometry and reduced risk of vertebral fracture as compared to control [60]. Maricic et al. [61] in 2002 in a post hoc analysis concluded that 12 months of raloxifene treatment reduces the risk of new vertebral fractures by 68% in general population and 66% in women who previously had a vertebral fracture. Thus, helped in reduction of greater risk for another fragility fracture.
2.2. Anabolic therapy
The most common anabolic medications include parathyroid hormone and its analogues like teriparatide and abaloperitide. The other anabolic agents explored to treat fractures are strontium ranelate, and certain biomolecules like sclerostin, bone morphogenetic proteins, fibroblast growth factor, platelet derived growth factor besides bone marrow grafts.
2.2.1. Parathyroid hormone and its analogues
Parathyroid hormone helps in regularization of mineral homeostasis. It is a naturally produced hormone by body. A drug in a form of Teriparatide (TPTD amino acid 1-34) has been developed to treat OP. Intermittent injection of such hormones and analogues to increase their serum concentration in body such as recombinant human parathyroid hormone (rhPTH), teriparatide (TPTD) and abaloparatide is a current regime to stimulate new bone formation. It increases bone mass and mechanical strength as well to some extent [62].
On meta-analysis (2016) of randomized and quasi randomized controlled trials comparing TPTD to placebo in the osteoporotic patients found accelerated fracture healing and better functional outcomes in osteoporotic women treated with TPTD [63]. Similarly, after reviewing results of few well-controlled retrospective studies, retrospective post hoc subetaoup analysis and randomized clinical trials in a systemic review published in 2017, it was suggested that TPTD provides selective advantage to fracture healing or functional recovery in the management of osteoporotic fractures [64]. In a randomized clinical trial on 40 menopausal women with proximal humerus fracture, no radiological signs of enhanced healing were noticed after daily injections of 20 mcg TPTD for 4 weeks, and it was suggested that better radiographs are required for understanding TPTD role in fracture healing [65]. The TPTD administration in patients with intertrochanteric fracture fixed with proximal femoral nail showed improved outcomes considering pain and quality of life [66]. In another study, TPTD showed better results after 6 months considering pain, fracture healing and functional score levels when compared to controls [67]. These studies [62]–[67] indicate that TPTD could be beneficial in treating osteoporotic fractures in future if studies can be carried out to find out effective dosage and treatment regimens for the same.
Parathyroid hormone-related protein abaloparatide is a synthetic analogue found to be effective in reducing vertebral and non-vertebral fractures. In rats, improved fracture healing was found when both TPTD and abaloparatide given in 1:2.5 ratio as compared to 1:4 in human OP trials [68]. The FDA has also approved it for the treatment of post-menopausal OP after a clinical trial conducted on 2463 ambulatory post-menopausal women [69].
Bone remodelling continues throughout life but is required to be accelerated whenever there is a fracture or compression in bones or deformities in articular surfaces. Daily injection of PTH or its analogues (abaloparatide or teriparatide) maintain calcium (serum and urinary levels) and phosphorous balance within physiological range resulting in increased bone mass and improving micro-architecture for functional strength [70],[71]. This check is done by PTH through increased RANKL and decreased osteoprotegerin production in osteocytes [72]; increased proliferation (by activating ERK1/2-m-togen-activated protein kinase (Extracellular-signal regulated Kinase 1 and 2, and phosphatidylinositol signalling pathways) [73] and differentiation of osteoblasts and inhibition of their apoptosis through trans-activation of runt-related transcription factor 2 (RUNX2) and cyclic Adenosine monophosphate/protein kinase (cAMP) [74]. It has also been noticed that PTH activates Wnt (Wingless-related integration site) signalling pathways of osteoblast lineage cells, osteoblasts and osteocytes after binding with their co-receptors (LRP5, LRP6)) related with low-density lipoprotein, receptor-related protein family activate beta-catenin thus increasing proliferation and differentiation of osteoblasts [75]–[77]. PTH has been found to reduce production of sclerostin, an osteocyte-specific protein which antagonizes Wnt signalling in bones [78], from osteocytes [79],[80]. Therefore, to harvest the beneficial effect of PTH on bone formation its usage be discontinued after 18–24 months before its resorptive action exceeds bone formation [81]. To enhance bone formation for longer period use of abaloparatide (instead of teriparatide) is suggested which increases trabecular thickness and its microstructure [82].
Teriparatide enhanced endochondral ossification through increased chondrocyte recruitment and differentiation [83] while PTH fastened the maturation of callus and improved biomechanical properties [84] by increasing regulatory T-cell population and balancing inflammation in early stages after trauma [85],[86]. It has been noticed that administration of PTH is required at supraphysiological dose rate to produce desired results but it warns a great risk of osteosarcoma [87] as the results regarding routes, timings, doses and duration of its administration are conflicting [88].
2.2.2. Strontium Ranelate (SrR)
Another anti osteoporotic agent strontium ranelate (SrR) works on bone replication to help new bone formation. Ozturan et al. [89] studied SrR effects (450 mg/kg/day) through creating a osteoporotic rat model by ovariectomy and heparin injection to induce OP. The experimental group had found higher fracture stiffness and mechanical strength as they developed more woven bone as compared to control group. It is said that SrR activates pre-osteoblasts in osteoporotic rats [90] and in a few clinical cases reports it was observed that strontium replaces calcium resulting in increased bone mass [91]. Beneficial effects of SrR were also reported on complicated long bone fracture healing [92]. Contrarily, adding SrR to calcium and vitamin D supplementation in patients older than 60 years age treated conservatively with manual reduction and cast application didn't reveal any accelerated wrist fracture healing [93]. Use of strontium ralenate as treatment for osteoporosis was authorized by the European Union on 21st September 2004. Previously it was available under the brand Protelos Osseor ®, later on it was removed from European Union market in August 2017 by ceasing its marketing and support on commercial reasons due to its safety usage related to cardiovascular system in patients treated with it.
The strontium ralenate has again returned to market in United Kingdom as an osteoporosis drug treatment in January, 2019. A pharmaceutical company ‘Aristo’ has now started manufacture of strontium ralenate and is available on prescription for treating OP specially in postmenopausal women and adults at high fracture risk who have no other effective choice of suitable treatment as stated by Dr. Nicola Peel from Royal Osteoporosis Society, UK.
2.3. Bone morphogenetic proteins
A family of peptide cytokines bone morphogenetic proteins (BMPs) pertaining to TGF beta are key tissues in development of regulators to induce ectopic bone formation. Functioning of different type of cells of osteoblast lineage, chondroblast lineage and mesenchymal stem cells have been found to be associated with pleiotropic effects of over 30 different types of BMPs to form bony tissues during embryonic and adult stages [94].
In animals, local administration of BMPs was found to be effective in fracture healing and spine fusion [95]. BMP-2, -4 and -7 accelerate chondrogenesis and osteogenesis around periosteum by initiating differentiation of mesenchymal cells in early stages of fracture healing [95],[96] while BMP-3 helps in bone remodelling by antagonising most osteogenic BMPs [95]. In various allogenic or autologous grafts of large and small animals to repair bone defects BMPs promoted healing [97]–[99] but clinical complications such as oedema, inflammation and heterotopic ossification restrict their usage [100]–[102].
Use of NEMO (NF-Kappa-B essential modulator) with BMP-2, have been reported to be effective in inhibiting NF-kappa B (Nuclear Factor “kappa-light-chain-enhancer” of activated B-cells) and thus reducing inflammation and oedema [103]. However, the short half-life and adverse clinical effects of BMPs restrict their usage in osteoporotic fractures.
Use of recombinant human BMP-2 (rhBMP-2) and recombinant human BMP-7 (rhBMP-7) was also approved by FDA in humans. For infusion in lumbar spine, maxillary sinus, alveolar ridge strengthening and open tibial fractures recombinant human BMP-2 (rhBMP-2) and recombinant human BMP-7 (rhBMP-7) for open tibial fracture was given approval in early 2000s [96]. Improvement in femoral defects of rat was seen when treatment included rhBMP-2 in conjugation with anti-sclerostin antibodies as compared with the group treated with anti-sclerostin antibodies alone.
Alternative methods have been explored to modulate BMP-2 signalling pathways using co-polymer-protected gene vectors or viral vectors within fracture site [104],[105]. Similarly, non-genetic approaches such as conjugating oilgoaspartic acid having affinity to hydroxyapatite at fracture site may be useful in promoting higher concentration of required agents for local gene transcription of growth factors [106].
2.4. Sclerostin
In mice targeted deletion of an autosomal recessive sclerostin gene has been found to increase bone formation [107] with excellent biochemical stability [108]. It has been noticed that sclerostin secreted by osteocytes inhibit low density lipoprotein receptor related protein 5 (LRP5) and/or lipoprotein receptor related protein 6 (LRP6) to locate receptors binding sites thus inhibits activation of Wnt signalling [109]–[111]. The sclerostin also promotes bone resorption by accelerating RANKL production in osteocytes [112]. Sclerostin also produces immune-neutralizing effect leading to increased rate of bone mass formation and biochemical stability at skeletal sites [113],[114].
Romosozumab, a highly specific monoclonal antibody neutralizes effect of human sclerostin, and it has been successful in decreasing risk of fractures in spine and hip of osteoporotic females by increasing bone mineral density [115]–[117].
2.5. Exogenous biomolecules
Intramedullary injection of exogenous genetic material regulating various growth factors, cytokines, chemokines and variety of signalling molecules have shown to boost osteo-metabolism in experimental animals [118]–[121].
Uninfected and aseptic, atrophic tibial diaphysis non-unions were treated after percutaneous autologous bone marrow grafting with aspirated bone marrow crests in 53 out of 60 patients [122]. A positive association was noticed between number of colonies forming units in pre-graft in-vitro cellular aliquots and the volume of mineralized callus. The number of these colonies in cellular aliquots from seven non-union cases was exceptionally low. It was concluded that autologous bone grafting in non-united factures is safe, but its success depends upon the technique of quality of harvesting bone marrow and cell preparation for the graft.
Injection of 0.4 or 2.4 mg recombinant fibroblast growth factor (FGF-2) hydrogel in transverse or oblique tibial shaft fracture site resulted in higher percentage of radiographically proven unions without any adverse effects in comparison to those infected with plain gelatine hydrogel as placebo [123].
A similar fusion rate and lesser side effects were found in treatment with platelet derived growth factor (PDGF), a peptide signalling molecule combined with beta tricalcium phosphate matrix in 260 patients (394 joints) requiring hind foot or ankle arthrodesis in comparison with the 137 patients (203 joints) treated with autologous bone graft from iliac crest [124].
3.
External stimuli to promote mechanical functioning
3.1. Electromagnetic field (EMF)
Application of electromagnetic field (EMF) is used to generate electromagnetic stimulus especially in non-union fractures [125]. Electromagnetic stimulus lead to 80% success in non-unions [126],[127]. Though its success was also demonstrated on delayed union of tibial fracture [128] but its effectiveness in fresh fracture was reported to be doubtful.
On the contrary, after a meta-analysis of 11 studies, it was concluded that the effect of EMF stimulation is insignificant on delayed union or non-union of long bone fractures [129].
In vivo effect of pulsed electromagnetic force (PEMF) applied three times per week for six months on 27 postmenopausal women was compared with placebo on 25 women by measuring bone marrow adiposity using magnetic resonance spectroscopy by Shaojun li et al. [130]. Application of PEMF produced significant (P < 0.05) increase in lumbar spine and hip bone BMD from 1.46% to 2.04%, the serum bone specific alkaline phosphatase increased by 3.23% and C-terminal telopeptides of type-I collagen (CTX) increased by 9.12%. No significant changes in BMD and these biomarkers were seen in placebo group.
The PEMF significantly increased bone specific alkaline phosphatase and beta-catenin concentration with simultaneous decrease in DKK-1 levels after 30 and 60 days, decreased CTX concentration at day 60, and decreased RANKL after 60 days without any significant changes in calcium, phosphorous, sclerostin and creatinine levels [131]. They noticed a negative association between rate of change in DKK-1 with beta-catenine and rate of change in sclerostin with RANKL/OPG (osteoprotegerin) ratio.
A statistically well-designed randomized placebo-controlled double-blind trial conducted by Ziegler et al. [132] revealed speedy osseous consolidation after high tibial osteotomy especially in patients over 50 years of age having poor bone metabolism on application of extremely low frequency electro-magnetic force of 16 Hz with 6-282-micron T intensity and 6mm amplitude emitted as group of pulses (bursts) in send-pause intervals for 7 minutes daily for 30 days. On comparing mean differences using two-tailed Mann-Whitney U-test (N = 48, two sided level of significance = 0.05, power of the test = 80% and confidence interval = 95%) the ELF-PEMF was found effective in increasing bone density, quick filling of osteotomy gaps from lateral to medial hinge (assessed by X-radiographs), an early increase in bone specific alkaline phosphatase (responsible for enhanced osteoblast genesis) without any adverse change in tartrate-resistant acidic phosphatase (TRAP 5b: responsible for osteoclast genesis), tumour necrosis factor (TNF alpha: responsible for inflammation), interleukin-6 (IL-6: responsible for inflammation), interleukin-13 (IL-13: regulating homeostasis) and monocytochrome attractant protein-I (MCP-I: responsible for oxidative stress) [132].
3.2. Low intensity pulsed ultrasound (LIPUS)
Pulsed ultrasound has been explored for accelerating fracture healing. In vivo animal and clinical trials have shown positive effect of low intensity pulsed ultrasound (LIPUS) on generation and activation of bone cells. It is expected that LIPUS produces pressure waves which induce favourable biochemical and molecular events at the cellular level but its role in accelerating healing of OP remains uncertain [133]–[138].
Jason W. Busse et al. (2002) suggested that ultrasound may be beneficial in fracture healing by producing signals to reduce healing time and disability period associated with delayed union and non-union of fractures leading to substantial cost savings [139],[140].
When a local infection occurs due to bacteria at the fracture site, it delays the process of fracture healing and could lead to non-union as well. In such septic environment fracture doesn't show radiological signs of healing. A surgical intervention may be required as infection adds significant delay in bone healing and make situation more challenging. A study on 49 patients has observed positive effects of 20 minutes/day LIPUS treatment along with antibiotics only. LIPUS has been found effective in reducing need for any surgical intervention in septic non-union circumstances [141].
LIPUS was found helpful in reducing time taken for facture union in three out of seven trial as compared to the placebo group in a study done by Raman Mundi et al in 2009. They included radial, tibial and lateral malleolar fractures in their studies. Whereas other four trials showed no significant results for the same [142].
Schandelmaier et al. [143] concluded that LIPUS could not reduce the time taken for full weight bearing and return to work. It was not even helpful in reducing in need for subsequent operation as well. Whereas a study published in 2017 by Yadollahpour and Samaneh Rashidi [144] used smaller and continuous mechanical stress along with LIPUS in their experimental group. Investigators suggested that this combination of treatment in a clinical setting was effective in callus formation and improved biological changes. It prevents bone loss and improves bone remodelling.
There were few drawbacks in above trials as sample size were small, risk of bias was present and inconsistent results. No review offered definitive conclusion hence extensive long term clinical and experimental studies investigating biophysical mechanisms of LIPUS quantifying its effect on bone formation and fracture repair are required.
4.
Physical exercises
In osteoporotic patients, physical exercises are effective to prevent and stimulate bone osteogenesis. In a National Health and Examination Survey (NHANES I, United States), women doing recreational exercise had 47% lower risk of hip fracture as compared to those doing little recreational exercise [145]. OP agencies like National Osteoporosis Foundation and International Osteoporosis Foundation recommend physical and weight bearing exercises throughout life to prevent OP in later stages [146]–[149].
A systematic review was published in 2013 by Mariana Barquet Carnerio et al. [150] on proximal femur fracture and their postoperative care. They studied findings of randomized controlled trials conducted during 2002–2012 and concluded importance of physical therapy in functional recovery of the elderly patients. Difficult follow up of elderly patients reduces the sample size and this limits the reliability of the study.
In a cohort study, regarding cost and effectiveness of protocol used in treating lower limb fractures Pishtiwan H.S. Kalmet (2018) concluded that permissive weight-bearing protocol has potential to be implemented on fractures of the pelvis and lower extremities and are beneficial along with surgical interventions in peri- or intra-articular fractures [151].
Based on analysis of retrospective observational scores obtained from medical records through hospital follow up of 294 patients Manuel Baer et al. [152] found contrary results on early mobilization and weight bearing. They noticed nil effects on pain and mobility of patients during their hospital stay.
Though there is scarcity of evidence and researches on the quantification of physical weight bearing and non-weight bearing exercises effects on fracture healing but they are definitely useful in preventing the associated fractures in high risk osteoporotic elderly population.
Helen Senderovich et al. in 2018 [153] reviewed scholarly articles to investigate the different exercises on high risk OP population considering fractures chances. They included both high and low impact exercises such as jogging, dancing and step aerobics in high whereas, walking and Tai-chi exercises in low impact exercises. They found that high impact exercises act as a barrier to the development of OP by reducing loss of BMD and bone stiffness, and low impact exercises demonstrated reduction in bone resorption levels while reducing the development of OP. The Tai-chi exercises also demonstrated helpful in attenuated bone loss in osteopenic post-menopausal women [153].
Based on the review dealing with studies on the effect of weight bearing aerobic exercise (walking, stair climbing, jogging) and strength and resistance exercises (swimming, cycling) it has been inferred that exercises have significant effect on BMD in osteoporotic women hence limiting risk of fractures in osteoporotic patients but long term exercises are needed to evaluate the complete effects [154].
Although these investigations reveal positive effect of exercises in prevention of osteoporosis but the quantification in terms of duration and type of physical exercise whether weight bearing or non-weight bearing exercises after fracture of specific bones needs well planned studies such that specific treatment and exercise protocols can be recommended for specific patients.
Principles of fracture prevention and physical rehabilitation of patients with osteoporotic vertebral and hip fragility fractures were discussed by Erhan and Ataker in 2020 [155]. They concluded that for vertebral fractures maintain stability at fracture site, limit bed rest, and if possible keep some bearable mobility of patient in acute phase; in early phase initiate thoraco-lumbar neuromuscular stability exercise, extend range of motion in upper and lower extremities, conservatively use orthosis to stabilize spine for 8–12 weeks, avoid resistance strengthening; in rehabilitation phase evaluate improvement radiologically, perform pain free exercise of dorsal extensor muscle strengthening to reduce kyphosis by protecting BMD, have surgery for vertebroplasty or kyphoplasty if pain persist. For hip fractures, keep hip in abduction during transportation, initiate rehabilitation at the earliest after surgical fixation to control pain, improve physical function and social participation to perceive quality of life, plan exercises for decreasing sarcopenia and improving muscle strength, balance, coordination and bone density, and organize surroundings to avoid future falls and fractures.
5.
Vitamin supplementation
Some important vitamins like Vitamin K and vitamin D play an important role in maintenance of healthy skeletal system as they help in regulating some minerals, especially the calcium metabolism.
5.1. Vitamin K
Vitamin K is a fat soluble vitamin, found as phylloquinone (K1) in plants, mainly in green vegetables (kale, spinach, broccoli etc.), herbs (sage, thyme, parsley etc.) and fruits (kiwi, grapes etc.) or as menaquinone (K2, MK4, MK7) synthesized in intestine by enteric bacteria and also found in foods of animal origin (cheese, eggs, meat, fermented soyabean or natto). It plays a major role in blood clotting. Its levels in blood may be affected by diabetes (impaired sugar metabolism), obesity (abnormal lipid profile) and old age (reduced endogenous production due to poor enteric bacterial activity and impaired digestion). Its role has also been recognized in bone mineralization by osteocalcin carboxylation, a protein derived from osteoblasts of bone marrow and cartilage responsible for bone matrix by promoting transition of osteoblasts to osteocytes and limiting osteoclast genesis [156] and due to its high affinity to calcium and hydroxyl peptide it improves calcium homeostasis [157]. Menaquinone activates nuclear factor kappa B [158] which improves bone remodelling, bone mineral density and reduces fragility fractures. Vitamin K supplementation has been approved in Japan for prevention and treatment of osteoporosis [159].
5.2. Vitamin D
Vitamin D is another fat-soluble vitamin supplied in diet from milk fat, fish and other sea foods. It is important to expose skin to sunlight for activating vitamin D availability. Fat consumption is restricted especially in elderly people due to its adverse effect on liver, arterial blockage, hypertension and impaired digestion. Old persons usually stay indoors due to restricted movements and have poor exposure to sunlight leading to vitamin D deficiency. About 90% of old people are deficient in Vitamin D and bone resorption rate in them can be reduced by supplementing 800 to 1000 IU of Vitamin D in their diet in the form of 25-hydroxy vitamin D. Such supplementation improves skeletal health and reduces fracture risk and pain. Poor adherence with calcium supplementation may result in improper vitamin D intake [160]. Vitamin D level below 50 nmol/l increases musculoskeletal ailments and incidence of tumours [161]. Around 95% of women may not get enough calcium and 50% of them have inadequate Vitamin D levels [162]. Out of 1515 postmenopausal women receiving anti-resorptive drugs one-third of women were Vitamin D deficient and vitamin D repletion was found essential to maximize response to raloxifene (60 mg/day), alendronate (70 mg/once a week) or risedronate (30 mg/once a week) for favourable BMD changes and anti-fracture therapy [163]. Vitamin D status was also significantly associated with BMD response to SrR (2 g/day) in post-menopausal osteoporosis at femoral neck but non-significant at lumbar spine. A positive relation was also noticed between BMD changes at femoral neck and alkaline phosphatase.
6.
Pain management
As defined by International Association of Study on Pain (ISAP), “chronic pain is an unpleasant sensory and emotional experience associated with actual or potential tissue damage or described in terms of such changes” [164]. Physiotherapy and therapeutic approaches to manage pain in osteoporosis for improving quality of life were reviewed by Catalano et al. [165]. The osteoporotic fractures cause acute pain (acute discomfort during homeostatic recovery) while severe OP without fracture cause chronic pain. Intensity of chronic pain is affected by several nociceptive, neural, cognitive, memory, emotional and social components. OP and sarcopenia (decrease of muscular tissue) often co-exist. They decrease daily life activities, increase risk of falls [166] and even in the absence of fractures may cause axial kyphosis and poor vertebral bone mass.
For pain management in OP multi-dimensional (physiotherapy, pharmacological and life style) approach is essential to improve quality of life. Physical pain therapy includes local or comprehensive application of electric, thermic and mechanical stimuli. In electric stimuli direct current or any low frequency simulated current comes where as in thermic a high frequency or sort wave thermic, ultrasound, light thermic, infra-red light can be used. A massage or stretching can be used in mechanical stimuli [167]. Muscle strength, coordination, body balance, circulation and sleep are improved by physical exercises, yoga, Pilates exercises and acupuncture. Cognitive behaviour therapy improves self-control, social contact, emotions and positivity to pain by separating sensory and emotional aspect of pain [168]. Vibration training increase neuromuscular coordination, physical fitness and relieves pain [169].
Non-steroidal anti-inflammatory drugs inhibit healing of injured bone and tendon due to their adverse effect on cyclo-oxygenase and prostaglandin activity [170]. Opioids [171], piroxicam [172], tapetadol [173], flurbiprophen and aspirin [174] are useful drugs to relieve pain without affecting healing process in osteoporosis but their side effects be taken care before prescribing them in different category of patients.
Surgically, pain due to osteoporotic ailments in spine could be managed by balloon kyphoplasty or vertebroplasty [165].
7.
Discussion
With the advances in medical and health facilities, protection against direct environmental adversaries and supportive lifestyles longevity of human being has been increased especially in developed and economically rich countries. With advancing age bones get weakened, become more porous, and fragile due to decrease in bone mass leading to higher incidence of osteoporotic fractures with delayed healing causing increased morbidity, disability and mortality.
Development of osteoporosis (OP) is silent with reduction in total bone mineral content. Decreased calcium and vitamin D levels, less mobility, low calcitonin, low estrogen, higher intake of alcohol, caffeine, sodium and animal protein, female gender, older age and genetics are important factors promoting OP. Bone mineral density is the most important parameter which can measure gravity of OP. The T-score of −2.5 or below indicates OP leading to fractures commonly in bones of spine, hip and distal extremities.
Pharmacological interventions stimulate bone formation process by triggering molecular pathways. Regular screenings along with physical exercises are targeted to prevent OP and accelerate fracture healing and subsequent functioning. Bisphosphonates like alendronate, risedronate, ibandronate and zoledronic acid have a significant role in improving BMD. The BP administration does not reduce time of fracture healing as they are the therapeutic agents to prevent OP while PTH promotes callus and endochondrogenesis [175], brides graft with surrounding bone [176], and enhances intracellular secondary remodelling [177].
PTH combined with BMP-7 improves mechanical function by integrating new bone tissue with old bone tissue, neither PTH nor BMP-7 alone can improve mechanization [178]. BMP-7 targets periosteal stem cells differentiation and is strictly anabolic facilitating bone repair only while PTH couples remodelling in underlined bone marrow space [176],[178]. BMP signalling constitutive with homeostasis of bone mass by stimulating Dickkopf protein and SOST through osteogenic cells in medulla [179]. Besides restraining morbidity and administering anti-inflammatory drugs in initial stages after fracture PTH, estrogen and bone morphogenetic proteins (BMPs), bio-molecules during critical stages of callus formation and bone remodelling, dietary changes with rich calcium and vitamin D diets, EMF for delayed-unions or non-unions, and LIPUS and physical exercises regimens during late stages for functional recovery are important interventions for complete fracture healing in osteoporotic patients. Among supportive therapies, the physical exercises could be beneficial before the fracture to minimize gravity of osteoporosis, EMF and LIPUS could be useful after surgical management of fracture or delayed and deformed union, and physical exercises again would be effective during late stages of fracture healing for better functional recovery.
8.
Conclusion
It is suggested that to prevent or reduce osteoporosis use of anti-resorptive medications in combination with physical exercises and healthy lifestyles are necessary. To identify the quantitative effect of these therapies in isolation or in combination clinical trials under proper experimental settings are particularly important so that inferences for different therapeutic regimes could be drawn.
Similarly, in the event of fracture in OP patients use of various medications and other interventions starting from day one of the fracture needs an optimum regimen depending on the site and gravity of injury due to fracture. Unlike the therapies for fracture repair in young and non-osteoporotic patients, the line of treatment and duration of each therapy in isolation or in combination with pharmacological agents, biological or biomolecular agents, physical stimulus, exercise and lifestyles are necessary. The specific therapeutic regimes may be optimized in patients treated with surgical interventions for allozygous or autozygous grafts and skeletal supporting devices specific for the specific site and individual patient.









 DownLoad:
DownLoad:



