Abbreviations: Behavioral Risk Factor Surveillance System (BRFSS); United States (US)
1. Introduction
The transformation of public health over the past century has resulted in a shift of focus from infectious disease to chronic disease and a resounding call for preventive medicine [1,2,3]. Though emphasis on preventive efforts has heightened in more recent years [4,5], advocates have long championed their importance. In a 1920 article, Charles-Edward Amory Winslow, an early pioneer in public health, describes the field as the science and the art of preventing disease, prolonging life, and promoting physical health [6]. Since this time the health community has made land mark changes by framing and establishing prevention guidelines which have been prompted by decades of research into the identification and promotion of healthier lifestyles [7,8]. This increase in prevention spurred by public health initiatives and health innovations has impacted life expectancy in the U.S. causing acceleration over the past century from barely 50 years to 78.8 years [9]. This tremendous success story has given rise to a large and expanding older demographic.
Current guidelines for healthy behaviors among the elderly exist, however, it remains unclear whether this growing proportion of the population has shifted their health behaviors and whether this has, in turn, improved the health of this broadening subpopulation. Some have suggested that there may be a decline in the acceleration of life-expectancy [10], whereas others have suggested we have not yet achieved our peak [11]. These views are both reasonable given extraneous factors such as diet, physical activity, medical advances, and population health initiatives. That is, if we continue our increases in these areas, we may very well continue our linear increase in life-expectancy. However, if we have reached our limit or lost effect in these areas, we will see a gradual decrement in the increase in life-expectancy in general with a greater decrement in certain subpopulations. Whether or not we are nearing the top of the life-expectancy curve, we must first consider what drives the nature of this curve and investigate continued positive trends in prevention approaches as well as modifiers that may be impacting healthy behaviors. We must equally investigate where trends have stalled or declined in search of more effective means. To gain an understanding of recent population trends we utilized a large population-level dataset complete with behavioral health metrics. The objective of this study was to investigate for trends of mental health and physical activity that may be leading indicators for trends in healthier living and increased life expectancy. This study will add further to the growing understanding of where future benefit and gain may be found.
2. Materials and Methods
2.1. Population and data sources
Behavioral Risk Factor Surveillance System (BRFSS) data over a near 10 year period from 2003-2011 were used in this analysis. BRFSS is considered the world’s largest ongoing telephone health survey system starting in 1984 and has collected data on health conditions and risk behaviors in more than 350,000 US adults each year since[12]. BRFSS data are generally considered valid and reliable [13,14], and estimates of health behaviors and chronic disease prevalence are consistent with other state surveys [15,16], despite an average response rate of approximately 50% which may influence generalizability. However, data are probability sampled by state among all households with telephones. Only one adult per household is surveyed. Weights are included in the public use data which are assessed from both landline and cell phone numbers to increase generalizability [17] and collected in a serial cross-section approach in all 50 states and the District of Columbia, Guam, Puerto Rico, and the US Virgin Islands allowing for trend analyses and prevalence estimation [18].
Data for this analysis consisted of variables available and standardized over the years spanning from 2003 through 2011. Data were complete for the metrics used in these analyses. In situations where variable indications or categories differed over the survey years, recategorizing was completed for consistency. Some indicators that would ordinarily have been included in these analyses were not included due to gaps in assessment over the near decade of time included in this investigation. A true cohort design with standardized questions would have been optimal though not available. Aggregated data over the years were restricted to those reporting age 65 or greater and in one of the 50 U.S. states. This resulted in 720,645 survey respondents for these analyses.
3. Demographic variables
Demographic variables considered in this analysis included: gender, age (categorized by year 65-75, 76-85, and 86 or older), marital status (married, never married, other), education (less than high school, high school or equivalent, attended college or technical school, college degree), income (< $15,000, $15,000 to $35,000, $35,000 to $50,000, > $50,000) race/ethnicity (White non-Hispanic, African American non-Hispanic, Asian non-Hispanic, Native Hawaiian or other Pacific Islander non-Hispanic, American Indian or Alaskan Native non-Hispanic, Hispanic, other), geographic region based on the census (West, Pacific, Midwest, South, Northeast), and year of survey submission (2003-2011).
4. Health and Behavior Variables
Health and behavioral characteristics considered for this analysis included body mass index (BMI) (normal/under, overweight, and obese), smoking status (never smoked, currently smokes, former smoker), physical activity, and mental health. Physical activity was assessed by the question, “During the past month, other than your regular job, did you participate in any physical activities or exercises such as running, calisthenics, golf, gardening, or walking for exercise?” and is considered comparable to other large surveillance systems [19]. A broad measure of mental health was assessed by the question, “Now thinking about your mental health, which includes stress, depression, and problems with emotions, for how many days during the past 30 days was your mental health not good?” where any days indicated was aggregated into a yes or no response variable.
5. Statistical Analyses
This serial cross-sectional survey assessment allowed for descriptive and univariate analyses of population levels as they pertain to physical activity and mental health. Weighted multivariable logistic regression was used to compare adjusted odds of physical activity and mental health while controlling for other demographic, health, and behavior related variables. Multicollinearity was assessed using the variance inflation factor, with a value greater than four suggesting presence of this condition. Mathematical weights were used in the statistical modeling to increase generalizability. Year of survey submission was included in the model for the yearly cross-sectional nature of the data capture. Standardized coefficients were calculated and classification tree analyses were conducted to present a graphical representation of the most influential variables. Data management and statistical analyses were performed using SAS software (version 9.1.3, SAS Institute, Inc., Cary, NC).
6. Results
Participants age 65 and older in BRFSS 2002 to 2011 with complete covariate data included a total of 720,645 survey respondents in this analysis. The sample consisted of 60.7 percent female, 61.3 percent 65 to 75 year olds, 49.2 percent widowed, separated or divorced, 35.3 percent with a high school diploma, 44.3 percent with an income between $15,000 and $35,000, 87.3 percent White non-Hispanic, 33.1 percent reporting from the southern region of the United States, 63.5 percent reporting overweight or obese, and 47.5 percent reporting having never smoked (Table 1). There were 68.4 percent of respondents who reported having participated in some type of physical activity over the past month and 19.7 percent who reported mental health issues on one or more days over a one month period.
Table 1. Physical activity, mental health, and study population characteristics of 720,645 respondents 65 or older from the Behavioral Risk Factor and Surveillance data, 2003-2011.
| Characteristic | Study Population N = 720,645 n (%) | Physical Activity N = 493,110 n (%) | Mental Health N = 141,868 n (%) |
| Sex | | | |
| Male | 283,300 (39.3) | 205,248 (41.6) | 42,502 (30.0) |
| Female | 437,345 (60.7) | 287,862 (58.4) | 99,366 (70.0) |
| Age | | | |
| 65–75 | 441,555 (61.3) | 316,051 (64.1) | 92,224 (65.0) |
| 76–85 | 230,417 (32.0) | 149,021 (30.2) | 41,909 (29.5) |
| 86 or older | 48,673 (6.8) | 28,038 (5.7) | 7,735 (5.5) |
| Race/ethnicity | | | |
| White nonHispanic | 629,076 (87.3) | 434,404 (88.1) | 121,295 (85.5) |
| Black nonHispanic | 41,308 (5.7) | 25,134 (5.1) | 9,243 (6.5) |
| Hispanic | 21,835 (3.0) | 13,973 (2.8) | 5,148 (3.6) |
| Asian nonHispanic | 7,793 (1.1) | 6,061 (1.2) | 1,180 (0.8) |
| American Indian/Alaskan Native | 6,629 (0.9) | 3,975 (0.8) | 1,745 (1.2) |
| Native Hawaiian/Pacific Islander | 604 (0.1) | 408 (0.1) | 147 (0.1) |
| Other | 13,400 (1.9) | 9,155 (1.9) | 3,110 (2.2) |
| Marital status | | | |
| Never married | 29,002 (4.0) | 19,678 (4.0) | 5,850 (4.1) |
| Married | 337,314 (46.8) | 246,118 (49.9) | 57,916 (40.8) |
| No longer married | 354,329 (49.2) | 227,314 (46.1) | 78,102 (55.1) |
| Education level | | | |
| No high school diploma | 95,201 (13.2) | 50,522 (10.3) | 22,407 (15.8) |
| High school diploma | 254,268 (35.3) | 159,700 (32.4) | 50,316 (35.5) |
| Some college | 174,798 (24.3) | 123,838 (25.1) | 35,473 (25.0) |
| College degree | 196,378 (27.3) | 159,050 (32.3) | 33,672 (23.7) |
| Annual household income | | | |
| < $15,000 | 114,773 (15.9) | 62,888 (12.8) | 30,203 (21.3) |
| $15,000 to < $35,000 | 318,996 (44.3) | 205,708 (41.7) | 66,005 (46.5) |
| $35,000 to < $50,000 | 117,990 (16.4) | 87,621 (17.8) | 20,708 (14.6) |
| > $50,000 | 168,886 (23.4) | 136,893 (27.8) | 24,952 (17.6) |
| Geographic region | | | |
| Northeast | 135,126 (18.8) | 92,109 (18.7) | 27,666 (19.5) |
| South | 238,523 (33.1) | 157,547 (32.0) | 45,897 (32.4) |
| Midwest | 169,532 (23.5) | 113,091 (22.9) | 32,044 (22.6) |
| West | 163,822 (22.7) | 119,871 (24.3) | 33,908 (23.9) |
| Pacific | 13,642 (1.9) | 10,492 (2.1) | 2,353 (1.7) |
| Body mass index | | | |
| Normal weight or under | 262,776 (36.5) | 191,917 (38.9) | 50,450 (35.6) |
| Overweight | 285,601 (39.6) | 202,332 (41.0) | 51,984 (36.6) |
| Obese | 172,268 (23.9) | 98,861 (20.1) | 39,434 (27.8) |
| Smoking status | | | |
| Never | 342,215 (47.5) | 239,222 (48.5) | 64,534 (45.5) |
| Prior | 307,918 (42.7) | 213,884 (43.4) | 59,469 (41.9) |
| Current | 70,512 (9.8) | 40,004 (8.1) | 17,865 (12.6) |
All findings were statistically significant based on a chi-square statistic consistent with a p-value less than 0.05. Those reporting proportionately less exercise than expected were those who were female, 76 years old or older, widowed, separated or divorced, educated with a high school diploma or less, categorized as having a lower income, living in the southern region of the United States, being obese, being a current smoker, and also reporting mental health challenges (Table 1). Those reporting proportionately more mental health challenges than expected were more likely to be female, 65-75 years old, widowed, separated or divorced, having less than a high school diploma, classified of lower income, being obese, and being a current smoker (Table 1).
Multicollinearity among variables was assessed with a variance inflation level of ≥ 4 indicative of an issue. Based on these investigations, no variables exhibited signs of multicollinearity and all variables were retained in further modeling. Two multivariable logistic regression analyses were run. In the first approach, physical activity was modeled as the outcome. In the second approach, the outcome was mental health. In both models, results were weighted for sampling differences and adjusted for sex, age, marital status, education, income, race/ethnicity, US geographic region, BMI, current smoking status, and year of survey submission (Table 2).
Table 2. Adjusted odds for physical activity and mental health among 720,645 respondents from the Behavioral Risk Factor and Surveillance data, 2003-2011.
| Characteristics | Physical Activity AOR (95% CI) | Mental Health AOR (95% CI) |
| Physical Activity | | |
| No | -- | 1.00 |
| Yes | -- | 0.78 (0.76–0.80) |
| Mental Health | | |
| No | 1.00 | -- |
| Yes | 0.78 (0.76–0.80) | -- |
| Sex | | |
| Female | 1.00 | 1.00 |
| Male | 1.24 (1.21–1.27) | 0.62 (0.60–0.64) |
| Age | | |
| 65–75 | 1.00 | 1.00 |
| 76–85 | 0.69 (0.68–0.71) | 0.84 (0.82–0.86) |
| 86 or older | 0.45 (0.43–0.47) | 0.68 (0.65–0.72) |
| Race/ethnicity | | |
| White nonHispanic | 1.00 | 1.00 |
| Black nonHispanic | 0.97 (0.93–1.02) | 1.08 (1.02–1.14) |
| Hispanic | 0.93 (0.87–1.00) | 1.16 (1.07–1.25) |
| Asian nonHispanic | 0.97 (0.82–1.16) | 0.92 (0.76–1.11) |
| American Indian/Alaskan Native | 0.92 (0.82–1.04) | 1.42 (1.23–1.64) |
| Native Hawaiian/Pacific Islander | 1.01 (0.67–1.53) | 1.30 (0.78–2.16) |
| Other | 1.04 (0.95–1.13) | 1.11 (1.01–1.21) |
| Marital status | | |
| Never married | 0.89 (0.83–0.93) | 1.08 (1.02–1.15) |
| Married | 1.00 | 1.00 |
| No longer married | 0.98 (0.96–1.01) | 1.07 (1.04–1.10) |
| Education level | | |
| No high school diploma | 1.00 | 1.00 |
| High school diploma | 1.26 (1.22–1.31) | 0.85 (0.82–0.88) |
| Some college | 1.67 (1.61–1.73)) | 0.93 (0.89–0.97) |
| College degree | 2.30 (2.21–2.39) | 0.93 (0.88–0.97) |
| Annual household income | | |
| < $15,000 | 1.00 | 1.00 |
| $15,000 to < $35,000 | 1.19 (1.15–1.23) | 0.77 (0.74–0.80) |
| $35,000 to < $50,000 | 1.50 (1.44–1.57) | 0.65 (0.62–0.68) |
| > $50,000 | 1.84 (1.76–1.92) | 0.56 (0.53–0.58) |
| Geographic region | | |
| West | 1.00 | 1.00 |
| Pacific | 1.00 (0.91–1.10) | 0.73 (0.66–0.81) |
| Midwest | 0.80 (0.77–0.82) | 0.83 (0.80–0.86) |
| South | 0.74 (0.72–0.77) | 0.72 (0.70–0.75) |
| Northeast | 0.77 (0.74–0.80) | 0.86 (0.83–0.90) |
| Body mass index | | |
| Normal weight or under | 1.00 | |
| Overweight | 0.83 (0.81–0.85) | 0.99 (0.96–1.02) |
| Obese | 0.47 (0.46–0.49) | 1.15 (1.11–1.19) |
| Smoking status | | |
| Never | 1.00 | 1.00 |
| Prior | 0.91 (0.89–0.93) | 1.13 (1.10–1.16) |
| Current | 0.52 (0.50–0.54) | 1.33 (1.28–1.39) |
In the first approach, where physical activity was modeled as the outcome and after controlling for all variables included in the model, adjusted odds of reporting physical activity participation in the past month was significantly higher among those not reporting mental health issues, participants who were male, 65-75 years of age, married, of higher education, of higher income, were from the western US geographic region, were categorized of normal or underweight, and who reported never smoking (Table 2). Additionally, earlier survey reporting years were associated with a statistically significant increased adjusted odds of physical activity (Table 2).
In the second model, where mental health was modeled as the outcome and after controlling for all other variables included in the model, adjusted odds of reporting mental health challenges in the past month was significantly higher among those who did not report having participated in physical activity during the past month, participants who were female, 65-75 years of age, non-married, of lower education, of lower income, were from western US geographic regions, were categorized as being obese, and current smokers (Table 2). Later survey reporting years were associated with the statistically significant increased adjusted odds of mental health challenges (Table 2).
Based on the standardized coefficients which provide a rank of the influence of each variable, higher education, normal weight, higher income, and never smoking were the most influential variables on reporting engagement physical activity. When considering better perceived mental health, the most influential variables were higher income, female, and living in the southern region of the United States.
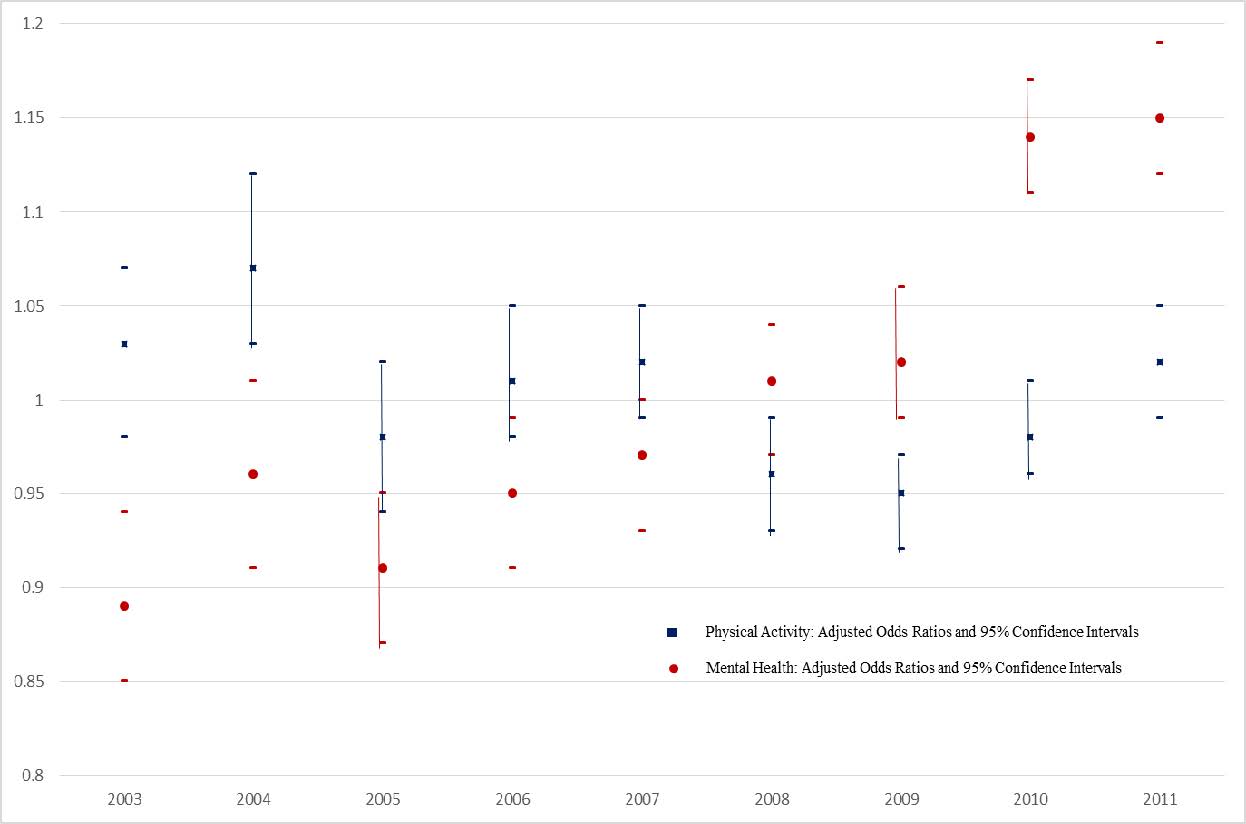
Figure 1 presents the adjusted odds of physical activity and mental health challenge per year when compared to the aggregate population of the other years combined and after adjusting for all other variables in the model. When holding all other variables constant, the adjusted odds of reporting mental health issues appears to increase over the near decade of data with an adjusted odds ratio (AOR) spanning from 0.89 in 2003 to 1.15 in 2011. This trend was not found with reporting of physical activity participation which, although some variability transpires, shows a relatively constant occurrence ranging from an AOR of 1.03 in 2003 to 1.02 in 2011.
7. Discussion
Significant advances in public health have provided abundant opportunities benefitting the overall health of our nation’s population and is highlighted by an annual increase in average life-span over the past century. The US population proportion of those 65 or older is projected to grow to nearly 22 percent by 2040 [20]. As a result, it will become increasingly more important to provide individually-centered as well as population-centered guidelines for healthy living [21,22]. Some have speculated that the enormous gains in life expectancy which we have witnessed over the past century are beginning to flatten while others believe we will continue strong life-span growth for years to come [10,11]. In this study, we selected two often intertwined measures of health to investigate trends over a near decade in time. Adjusted odds of physical activity and mental health were assessed in a large population of participants from the BRFSS yearly cross-sectional study over the period of 2003 to 2011. Findings suggest that there are several factors that are consistent between the two outcomes such as higher income, higher education, current smoking, and BMI that impact negatively both mental health and physical activity. Further, though public health professionals may have the perception that physical activity is increasing due to increased educational efforts, these data provided a fairly level reporting in physical activity participation in this subpopulation of respondents greater than 65 years over the time period. Perhaps more important and alarming was the noticeable increase in adjusted odds of mental health over the same time period, which may be a leading indicator of decreases in physical activity.
Physical activity is a key factor during all ages of life, promoting both physical and mental health well-being [23,24]. Physical activity in an aging population has been shown to have enormous positive impact towards decreasing mortality for many of the chronic diseases that are ailing this group of the population and participation in physical activity is also highly considered when determining health status [25,26,27,28,29,30]. To that end, significant effort has been put forth to present guidelines for this population. However, many factors such as retirement [31,32], changes in sleep patterns [33], declining muscle mass [34], disability [35,36], and others have been reported to reduce physical activity. In the current study, factors consistent with past research were seen as being influential in association with increased participation in physical activity including being male, higher educated, higher income, living in the western US region, being of normal weight, and never smoking [37,38,39,40]. Holding these factors constant, however, there appeared to be no increasing trend in physical activity participation over the near decade of data in this study. In turn, as the population continues to age among an unrelenting obesity epidemic, we might have expected physical activity participation to decrease over this time period. The steady state, alternatively, may suggest victories in public health physical activity campaigns as well as indicate that other factors intertwined need to be parsed out.
Mental health is a complex multi-faceted construct with many domains that impacts health in substantial ways [41]. Reports have suggested that one in four Americans will experience a diagnosable mental health disorder in any given year with an estimated life-time prevalence of nearly half of the population [42,43]. Another report suggests that 20.4 percent of those 65 and older meet criteria for a mental disorder in a 12-month period [44]. The current data are consistent with these and other reports and suggests a 19.7 percent prevalence of reporting mental health challenges in the previous 30 days among those 65 years of age or older. When breaking down this broader age group, mental health challenges over the past month were reported among 20.9 percent of those between 65 and 75 years of age, 18.2 percent among those 76-85 years of age, and 15.9 percent among those 86 or older (weighted prevalence estimates are reported). The multivariable adjusted and weighted regression model presents a similar picture with odds of mental health challenges appearing to decrease with age when compared to 65 to 75 year olds. Further research may be warranted to help elucidate reasons for lower odds of mental health challenges in these oldest age groups. Regardless of these potential differences in higher age groupings, an Institute of Medicine (IoM) 2012 report highlighted the insufficient supply of trained mental health professionals able to provide mental and behavioral health services to the growing elderly population [45]. With the increase in adverse mental health reporting over time shown in the current study, and in conjunction with the inflating proportion of this older segment of our population, this shortage of trained mental professionals is likely underestimated.
Health guidelines that are provided to promote a healthy population are a culmination of evidence-based research and actionable information presenting a course forward to many who would be otherwise unassuming in a quest for better health [40,46,47,48]. Independent of other factors, however, these guidelines often present an isolated approach to an otherwise holistic continuum of health. In the current analyses, there appeared to be a decreasing trend in adverse mental health reporting over the near decade of data while keeping all other factors in the model constant. Physical activity in these same data, however, appeared to be constant for this population at a time when education enhanced public knowledge and should have resulted in slight but steady gains in physical activity. One may conclude that recent past public health initiatives and the guidelines put forth from them aimed at educating this and younger populations are no longer as effective. We must also consider that a broader view of guidelines encompassing a multi-factorial approach to improving overall population health may be far more successful in achieving further advances in life-expectancy. Future public health gains will be measured in small advances and among sub-populations by simultaneously recognizing the many factors that compete for the health of our elderly.
Understanding the limitations and strengths of this study is essential in understanding what type of information it may provide to both researchers and practitioners. First, likely most impactful, is the fact that these data were cross-sectional in nature and will not allow individualized temporal sequence alluding to causality [49,50]. This does present a strength as well due to less resource and time commitment when compared to cohort studies allowing for association investigation [51]. The result is that we could aggregate a large amount of data with many factors over several years allowing for population-level temporality and calculation of adjusted and unadjusted associations rather than estimates of risk. In the same context, there may be data that more specifically assess for the goals of this study but in select or limited sub-populations and would not allow extrapolation to such a broad population as we did. Further, self-reported data are inherently limited and present possible biases though in these analyses likely non-differential. Findings, if effected, would be expected to be biased towards the null [52]. Additionally, self-reported mental health and physical activity are imperfect and often blunt surrogates for a physician’s assessment. A more granular assessment may yield non-differential misclassification resulting in estimates, again, most likely biased towards the null [53]. Generalizability of these data offers a limitation to the ability of making speculations about the entire population. In this study, we have focused on the U.S. population over the age of 65 through the use of BRFSS data which do not include information from institutionalized populations or those without land or cellular phones. Still, the BRFSS data are obtained from all states and offer sampling weights that provide another step closer towards generalizing to the larger U.S. population. Lastly, the objectives of this study were to investigate physical activity and mental health over a decade period of time. The questions utilized from the survey instruments were broad in nature and have not been validated or proven to be reliable in this population for specific assessment of mental health or depression. Strengths of this study not already mentioned include the ability to aggregate 10 years of data and use standardized variables over the time period allowing for the adjustment of many variables that may be associated with the outcome or exposure. Lastly, the use of robust statistical software and procedures with the inclusion of weights for unadjusted and adjusted results allowed for better inferences and interpretation of the results.
As public health professionals struggle to understand the constellation of factors that contribute to wellness including the many interactions that may be present, there are a few factors known to be foundational factors. In this study we focused on two of those factors, physical activity and mental health in an attempt to investigate trends over a near decade of time while holding other important and evolving demographic, sociodemographic, and health behaviors constant. This allowed for a more comprehensive view of this in a large and generalizable population. The concept of health is a multifaceted complex continuum of exposures and behaviors encompassing mental, physical, and social well-being requiring a holistic strategy. The current approach of public health initiatives in promoting health in an aging population of US adults would benefit greatly with further integration of mental health promotion with prevention initiatives that focus on physical activity, nutrition, and other behavioral recommendations.
Acknowledgements
The views expressed in this article are those of the authors and do not reflect the official policy or position of National University or University of California, San Diego. We thank the BRFSS team for surveying, cleaning, and managing these data and for putting them forward for research purposes as a public use data file. We are indebted to the BRFSS participants, without whom these analyses would not be possible.
Funding Source
For TSmith, this research was conducted with time given by the National University Presidential Scholar Award for course reduction. For BSmith, this research was conducted with no support financial or otherwise.
Financial Disclosure
The authors have no financial relationships relevant to this article to disclose.
Conflict of Interest
The authors have no conflicts of interest to disclose.
Implications and Contribution
There has been much focus on establishing physical activity guidelines for elderly populations. Influential factors, however, may impact this message and translating these guidelines into practice may be challenging in light of other factors. This study investigates physical activity and mental health in the large and growing segment of elderly in the population and further investigates areas where future benefit and gain may be found.









 DownLoad:
DownLoad: