1. Introduction
The use of various sources of renewable energy becomes increasingly important in the worldwide effort of ameliorating problems associated with the use of fossil fuels. No doubt that solar energy is one of the most attractive sources of clean energy. Among different solar energy technologies,concentrated solar thermal power(CSP)is believed to be very promising for large-capacity power generation. Due to the possibility of incorporating solar thermal storage into the power generation system,CSP can better meet the power dem and at the time sun is down [1,2,3,4].
In the past decade we have seen a worldwide significant increase in solar thermal power generation capacity with the combination of solar thermal storage. The number of solar thermal power plants constructed in Southern Europe,USA,Africa,and Australia is increasing,which generate electricity by replacing conventional fuel-combustion facilities in power plants with solar thermal collection devices. Solar concentrators collect thermal energy and raise the temperature of the heat transfer fluid(HTF),which is fed to a heat exchanger and boils water into steam of high temperature and high pressure. The steam subsequently drives steam turbines,which generate electricity. There are four types of solar concentration technologies,parabolic trough,solar power tower,Fresnel reflectors,and solar dish Stirling engines. The first three use a HTF to take away the heat from the collectors and use the heat in power generation systems.
Heat transfer and heat storage are the two important roles of a HTF in concentrated solar power systems. The well-known HTF used in CSP systems in the earlier stage is made of organic substances,which is an eutectic mixture of biphenyl(C12H10) and diphenyl oxide(C12H10O),sold under the br and name of Therminol VP-1 and Dowtherm A [5,6]. It exhibits a low melting point of 12 °C(285 K)but is limited to an upper temperature of 390 °C(673 K)due to chemical dissociation above this temperature. This is not sufficiently high for the increasing dem and of thermal efficiency of a CSP system. The high vapor pressure(10 atm at 390 °C) and high cost of this HTF also significantly restrict its application.
Increasing the high temperature in a CSP plant from 390 ℃ to 500 ℃(using molten salts)would increase the Rankine cycle efficiency to the 40% range(compared to the efficiency of 37.6% using Therminol VP-1) and thereby reducing the levelized electricity cost by 2 cents/kWh [7,8]. For more development of CSP technologies,finding a heat transfer fluid working at much high temperatures is important.
There are multiple dem and s if a fluid serves as a heat transfer fluid in a large range of temperature variation. First the fluid should have a low freezing point to avoid solidification in the circulation system. Second,the fluid should be chemically stable at a high temperature,and at the same time to have low vapor pressures(below 1.0 atm)due to the safety requirement of containers and pipes. Third,the fluid must have minimum corrosion to the metal pipes and containers that hold the fluids. Forth,the heat transfer fluid should have favorable transport properties(low viscosity and high thermal conductivity)for efficient heat exchange and low pressure loss in the flow and circulation.
Molten salts have been studied for their possibility of high working temperatures,and in the meantime with low melting points,moderate density,high heat capacity,and high thermal conductivity. Other than favorable thermal and transport properties,long term thermal stability(or chemical stability with less corrosion to containers) and low cost of molten salt HTF is also very critical [9,10,11,12].
Due to the very strong dem and ,the research work for suitable molten salts for HTFs as well as thermal energy storage materials in solar thermal power plants [13,14] is very active recently. The studies on some inorganic salts used for thermal energy storage materials are available in several papers [15,16,17,18,19]. Zalba et al. [16] summarized thermal characteristics of some phase-change materials. Kenisarin [17] and Gil et al. [18,19] analyzed some phase change materials and the practical applications for solar thermal storage. So far,several well-recognized commercial molten salts by eutectic mixtures of nitrates or nitrites have been used in concentrated solar power systems mainly for thermal storage purpose,but can also be used as HTF. A binary mixture,Solar Salt(60 wt.% NaNO3/ 40 wt.% KNO3)has been used as thermal storage material in the 10 MWe solar-II central receiver project in California [20,21,22],in the 2-tank direct system of the Archimede project in
Italy [23],and the indirect thermal energy storage system for the Andasol plant in Spain [24,25].Solar Salt has a thermal stability(below 600 ℃) and a relatively high melting point(220 ℃). A new heat transfer fluid called Hitec,which is a ternary salt mixture of 53 wt.% KNO3/ 7wt.% NaNO3/
40 wt.% NaNO2,has been considered to replace the Solar Salt because of its low freezing point of
142 ℃ [26]. Hitec is thermally stable at temperatures up to 454 ℃,and may be used at temperature up to 538 ℃ for a short period [27]. A modified version,Hitec XL,is a mixture of 48 wt.% Ca(NO3)2/ 7 wt.% NaNO3/ 45 wt.% KNO3 which melts at about 133 ℃ and may be used at a temperature up to 500 ℃ [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]. Different compositions of Ca(NO3)2/ NaNO3/ KNO3 have been identified in the open literature as eutectic salts [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]. The ternary eutectic salt with composition of 44 wt.% Ca(NO3)2/ 12 wt.% NaNO3/ 44 wt.% KNO3 melts at 127.6 ℃ and its thermal stability is good at up to 622 ℃ [43]. Different phase diagrams also have been published for the Ca(NO3)2/ NaNO3/ KNO3 system [44,45,46,47].
There are also other ternary salts being developed and undergoing tests for industrial application. The eutectic salt in composition of 25.9 wt.% LiNO3/ 20.0 wt.% NaNO3/ 54.1 wt.% KNO3 melts at about 118 ℃ and thermal stability is up to 435 ℃ [48,49]. The salt in composition of 30wt.% LiNO3/ 18 wt.% NaNO3/ 52 wt.% KNO3 is reported to have thermal stabilities up to 550 ℃ and melting point of 120 ℃[50,51,52]. Another ternary nitrate salt mixtures consisting of 50-80 wt.% KNO3/ 0-25 wt.% LiNO3/ 10-45 wt.% Ca(NO3)2 melts below 100 ℃ and thermal stability is up to
500℃ [53]. S and ia National Laboratories developed a low-melting heat transfer fluid made of a mixture of four inorganic nitrate salts: 9-18 wt.%NaNO3/ 40-52 wt.%KNO3/ 13-21 wt.%LiNO3/20-27 wt.% Ca(NO3)2 [54]. This quaternary salts mixture has a melting temperature less than 100 ℃ and the thermal stability limit is greater than 500 ℃. The quaternary salt 17.77wt.% LiNO3/ 15.28 wt.% NaNO3/ 35.97wt.% KNO3/ 30.98 wt.% 2KNO3·Mg(NO3)2 melts at about 100.9 ℃ but there is no data about thermal stability [55]. Another quaternary nitrate salt mixture consisting of 17.5 wt.% LiNO3/ 14.2 wt.% NaNO3/ 50.5 wt.% KNO3/ 17.8 wt.% NaNO2 has a melting point of 99 ℃ and thermal stability at up to 500 ℃ [56]. Eutectic mixture with five species of salts also has been developed,for example,the salt with compositions of 6wt.% NaNO3/ 23 wt.% KNO3/ 8 wt.% LiNO3/ 19 wt.% Ca(NO3)2/ 44 wt.% CsNO3 melts at 65 ℃ and has thermal stability of up to 561 ℃ [29]. Nevertheless,nitrate and nitrite salt systems have been found not thermally stable at temperature above 600 ℃ from a large amount of research works. A summary of the above mentioned HTFs is in Table 1.
Table 1. Summary of the key data of some heat transfer fluids.
| Name | Formula | Tmelt(℃) | Tmax(℃) |
| Therminal VP-1 | (C12H10) and (C12H10O). Percentage not know. | 12 | 390 |
| Solar Salt | wt. 60% NaNO3 /40% KNO3 | 220 | 600 |
| Hitec | wt. 53% KNO3/7% NaNO3/40% NaNO2 | 142 | 454-538 |
| Hitec XL | wt. 48% Ca(NO3)2/7% NaNO3/45% KNO3 | 133 | 500 |
| NS-1 | wt. 44% Ca(NO3)2/12% NaNO3/44% KNO3 | 127.6 | 622 |
| NS-2 | wt. 25.9% LiNO3/20.0% NaNO3/54.1% KNO3 | 118 | 435 |
| NS-3 | wt. 30% LiNO3/18% NaNO3/52% KNO3 | 120 | 550 |
| NS-4 | wt. 50-80% KNO3/0-25% LiNO3/10-45% Ca(NO3)2 | 100 | 500 |
| NS-5 | wt. 17.77% LiNO3/15.28% NaNO3/35.97% KNO3/ 30.98% 2KNO3·Mg(NO3)2 | 100 | |
| NS-6 | wt. 17.5% LiNO3/14.2% NaNO3/50.5% KNO3/ 17.8% NaNO2 | 99 | 500 |
| NS-7 | wt. 6% NaNO3/23% KNO3/8% LiNO3/ 19% Ca(NO3)2/44% CsNO3 | 65 | 561 |
A target of high temperature at 800 ℃ for CSP has been proposed by US Department of Energy. This is possible to accomplish Brayton power cycle,which can further increase the heat-to-electricity efficiency. Therefore,it is proposed recently to replace molten nitrate-nitrite salt with other kinds of salts to possibly increase the applicable temperatures to the level of 800 ℃ and even up to 1000 ℃. Hundreds of inorganic salts and salt composites for HTF and latent heat storage in the temperature ranging from 120 ℃ to 1000 ℃ are listed in Kenisarin’s review paper [57]. Those materials are on the basis of chlorides,fluorides,bromides,hydroxides,nitrates,carbonates and other salts. He found out that almost no single inorganic salt possesses decent properties to serve as a qualified HTF. Binary and ternary eutectic compositions based on fluorides and chlorides are the most prospective materials in term of their possibly favorable thermal and transport properties,as well as reasonably low cost in particular.
The eutectics of fluoride salts have been utilized in space solar power and molten salt nuclear reactors because of their favorable thermal and transport properties,especially heat storage capacity,but with the disadvantage of high cost,material compatibility and toxicity [58,59,60]. Carbonates may also be used for high temperature HTF and latent heat storage materials,but with drawbacks of high viscosity and easy degradation [61,62]. Consequently,chlorides salts are attractive due to their possibly favorable properties and especially low cost [63].
Funded by U.S. Department of Energy,a team by researchers from the University of Arizona,Georgia Institute of Technology,and Arizona State University has been conducting studies to ternary,quaternary and even higher order eutectic salts based on five key species of halide salts—AlCl3,ZnCl2,FeCl3,NaCl,and KCl. These species are relatively inexpensive and also have great amount of reserve on the earth. The mixing of these ionic and covalent salts is expected to create favorable properties needed for HTF.
It is underst and able that ionic and covalent halide salts are different in molecule size,shape,and chemical bonding. The bonding of positive ion and negative ion can make disorder leading to eutectic mixture with low melting temperatures. In Figure 1,strong evidences of low melting points at some eutectic compositions are shown in the phase diagrams of some binary and ternary mixtures by halide ionic salt with covalent salt(NaCl-AlCl3,KCl-AlCl3,NaCl-ZnCl2,KCl-ZnCl2,NaCl-KCl-AlCl3,NaCl-KCl-ZnCl2). Although very promising,a significant amount of work needs to be conducted to fully underst and all the properties of these salts mixtures.
Obviously,identifying the eutectic compositions that have low melting points is only the first step of developing a HTF. As the final goal,a HTF should meet the target of thermal and transport properties in a relatively wide temperature range from below 250 ℃ to at least above 800 ℃. To obtain the thermal and transport properties(vapor pressure,density,viscosity,specific heat,thermal conductivity)for a high order mixture(of ternary and quaternary components),the properties of all individual components as well as all the low-order salt mixtures have to be identified. For this purpose,the present paper reviews the currently available experimental data for density,viscosity,
thermal conductivity,specific heat capacity,vapor pressure,and melting point of several halide salt single species as well as their binary to ternary mixtures. These data are expected to serve as the basis for further work of developing high order eutectic mixtures with underst and ing of their thermal and transport properties.
2. Properties of Several Popular Single Halide Salts in Molten State
In this section,the thermal and transport properties of the five single species of molten salt(AlCl3,ZnCl2,FeCl3,NaCl,KCl)are provided for reference and evaluation on whether a salt can contribute to a better property of a possible eutectic salt mixture.
2.1. Aluminum chloride(AlCl3)
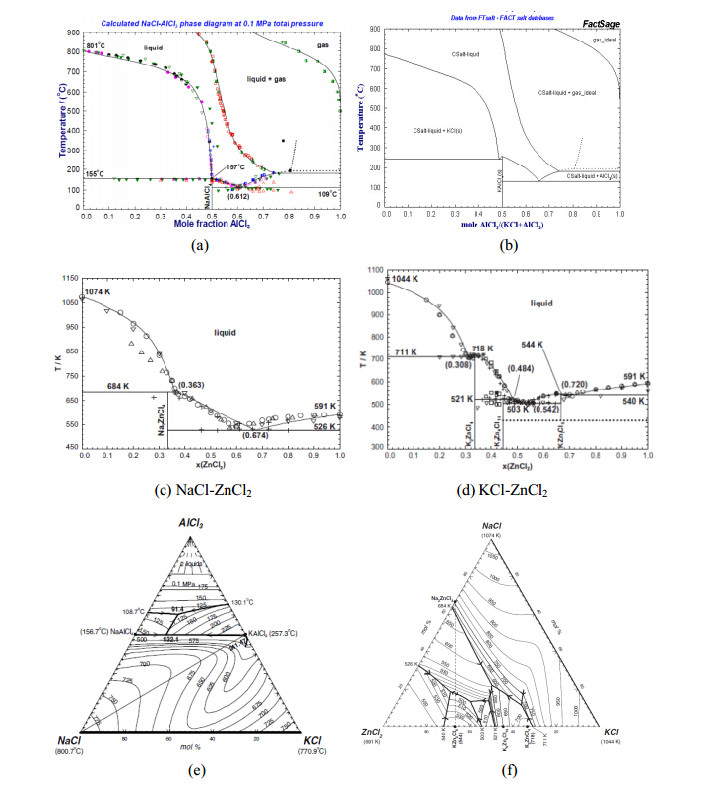
This salt has a relatively low melting point which is Tm = 465 K(192 ℃)[66]. However,it sublimes early at a temperature of 180 ℃. The surveyed properties for molten AlCl3 [66] are shown in Figure 2. The properties as functions of temperatures are given by the following equations:
| ρ=3.7660038−1.3346×10−2T+2.7622×10−5T2−2.2331268×10−8T3 |
(1)
|
where the units are p(g/cm3),T(K)in the range of 465-560 K.
| μ=3.2146−9.6606×10−3T+7.4554×10−6T2 |
(2)
|
where the unit of viscosity is 10-3(Pa s),and temperature is in K,in the range of 470-560K. The low viscosities may make AlCl3 a very good component for a eutectic salt mixture as the low viscosity is important to a HTF.
| Pvap=10(7.42055−1948.55/T) |
(3)
|
where the unit of pressure is Pvap(mm*Hg = 133.32 Pa),and the temperature is in K,in the range of 455-530K.
The s pecific heat capacity of liquid AlCl3 does not change greatly in a wide range of temperatures from466-1500K,which is around Cp=125.5 J/mol*K or equivalent to 941.2J/kg*K [67].
The vapor pressures of AlCl3 are quite high which are not favorable as a heat transfer fluid. It is thus expected that ionic salts in a eutectic mixture with AlCl3 can create inter-molecular bonding to suppress the vapor pressure. There are no thermal conductivity data found for liquid AlCl3 in the current survey.
2.2. Zinc chloride(ZnCl2)
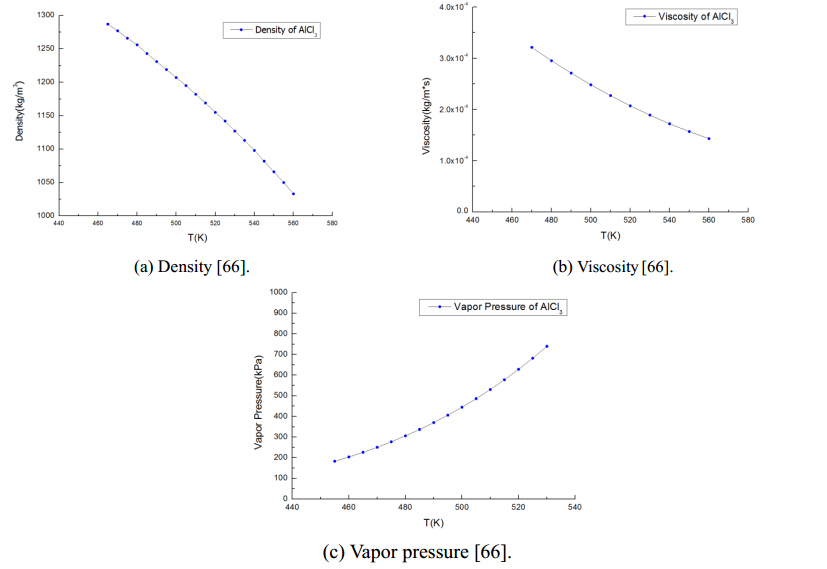
Due to the low melting point and relatively low vapor pressure(compared to that of AlCl3),ZnCl2 is a very important species in halide salt family to contribute to a low melting point in a eutectic salt. The melting point of ZnCl2 is Tm = 556 K(283 ℃)[68]. Other properties are summarized as follows.
The density,viscosity,and vapor pressure of molten ZnCl2 versus temperatures are shown in Figure 3. The expressions for these properties as function of temperatures are given in Eqs.(4)-(6).
| ρ=2.424−0.00046×(T−773) |
(4)
|
where the units are p(g/cm3),T(K),and the equations is applicable in a temperature range of 758.7-823.7 K.
| ln(μ)=0.2686−2665730.8×ln(T)/T2+19840539/T2 |
(5)
|
where μ is in cp or 10-3 Pa s,and T is in(K); the range of temperature is in 571-893K.
It is interesting to see from Figure 3(b)that the viscosity at low temperatures is high but it decreases dramatically when temperature increases. The low viscosity at high temperature is advantageous; while the high viscosity at low temperature should be modified by adding other components in a eutectic salt mixture.
The vapor pressure of liquid ZnCl2 is relatively low compared to that of AlCl3. As shown in Figure 3(c)the vapor pressure of ZnCl2 is quite low at temperatures below 600 ℃,and at around 800 ℃ the vapor pressure reaches 2.0 atm. The correlation of vapor pressure and temperature reported by Keneshea and Cubicciotti [69] is in the form of
| logp(mmHg)=(−8415.2/T)−5.034logT+26.420 |
(6)
|
where the unit of temperature is K,mm*Hg = 133.32 Pa. The relatively low vapor pressure of ZnCl2 compared to that of AlCl3 makes it a more favorable component to contribute to a relatively lower vapor pressure in a eutectic salt mixture.
The specific heat capacityin the temperature range of 591-973K is around 24.1 cal/mol*K[70],or 739.54 J/(kg K). The present review could not find thermal conductivities for molten ZnCl2.
2.3. Iron(III)chloride(FeCl3)
The melting point of salt FeCl3 is Tm = 555 K(282 ℃)[68]. The specific heat capacity of molten FeCl3 is Cp = 133.89 J/mol*K or 825.43 J/kg*K in the temperature range of 577-1500 K. This salt has a rather high vapor pressure as shown above in Figure 4. At about 340 ℃ the vapor pressure already reaches 2 atm [73]. For this salt to be a component in a eutectic salt mixture,its high vapor pressure can be a problem of concern. No other properties were found for molten FeCl3 in this survey.
2.4. Sodium chloride(NaCl)
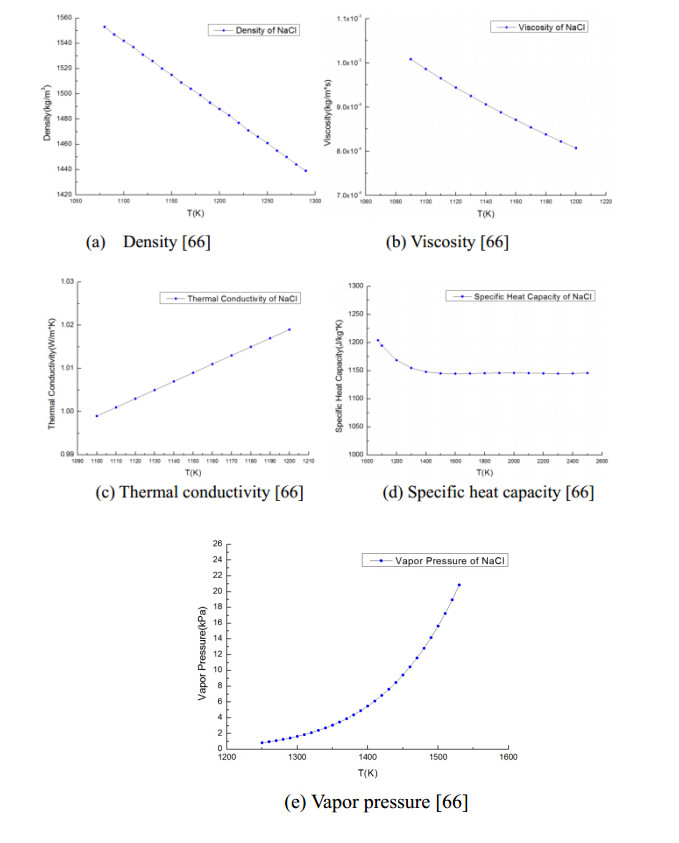
Well known as the table salt,NaCl has a melting point of Tm = 1075 K(802 ℃)[66]. NaCl also has an almost unlimited reserve in seawater and thus has relatively low cost. Properties of molten NaCl are surveyed and given in Figure 5.
The correlations of the properties were given in Eqs.(7)to(9). For density there is
where the units are p(g/cm3) and T(K). The equation is applicable in the range of temperature of 1080-1290 K.
The expression of viscosity is
| μ=0.08931exp(5248.1/RT)) |
(8)
|
the unit of viscosity is μ(cp) and that of temperature is T(K),the range of temperatures for this equation is 1090-1200 K and the universal gas constant is R = 1.98716(cal/K*mol). The relatively low viscosity of molten NaCl is favorable for it being used as a component in a eutectic salt mixture,which needs to have low viscosities at high temperatures.
The expression of thermal conductivity is
| k=1.868×10−3+4.73×10−7T |
(9)
|
where k has unit of(cal/cm*s*K = 418.4 W/m-K),and T is in(K),for the range of 1100-1200 K.
The expression of specific heat capacity is
| Cp=−42.4478+113.526×t−43.6466×t2+5.89663×t3+39.1386/t2 |
(10)
|
where unit of Cp is J/(mol*K),t = T(K)/1000,and T is in(K). The equation is applicable in a range of temperature from 1074 K to 2500 K.
The vapor pressure in a narrow temperature range for molten NaCl is expressed as:
| Pvap=10(8.4459−9565/T) |
(11)
|
where Pvap is in(mm*Hg = 133.32Pa),T is in(K),and the range of the temperature for the equation is 1250-1530 K. The low vapor pressure of molten NaCl is very favorable for a heat transfer fluid.
2.5. Potassium chloride(KCl)
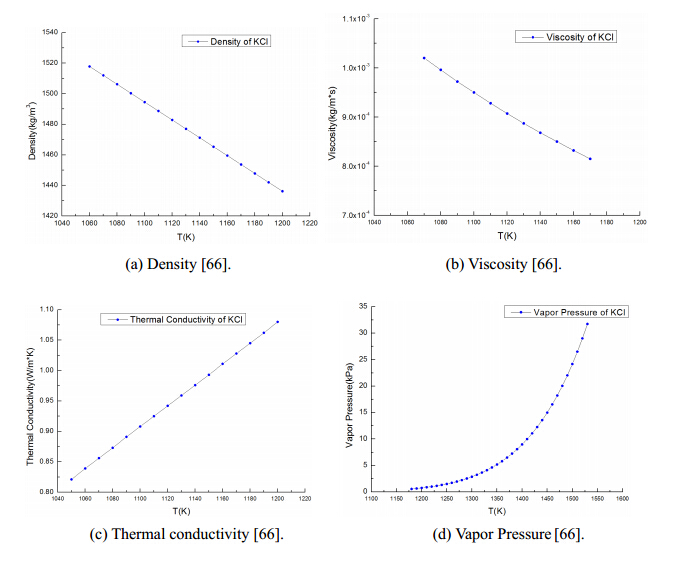
Potassium chloride has a melting point of Tm = 1043 K(770 ℃)[66]. The properties surveyed for molten salt KCl are given in Figure 6. The corresponding expressions of the properties against temperatures for the curves are given in Eqs.(12)to(15).
For density,there is
| ρ=2.1359−5.831×10−4T |
(12)
|
which is applicable in a temperature range of 1060-1200 K,the unit of density is p(g/cm3) and for T is(K). For viscosity there is
| μ=0.0732exp(5601.7/RT) |
(13)
|
where the unit of viscosity is μ(cp or 10-3 Pa s),T(K)is temperature,and R = 1.98716(cal/K*mol). The equation is applicable in a range of 1070-1170 K. The relatively low viscosities of this molten salt make it a favorable component for a eutectic salt mixture. The thermal conductivity is
| k=−23.43×10−4+4.103×10−6T |
(14)
|
where k has unit of cal/(cm*s*K = 418.4 W/m-K),temperature T has unit of(K),and the equations is applicable in the range of1050-1200 K. The thermal conductivities of molten salt KCl are slightly lower than that of molten NaCl.
| Pvap=10(8.2800−9032/T) |
(15)
|
where Pvap(mm*Hg = 133.32Pa)is vapor pressure,and T(K)is temperature which is in the range of 1180-1530 K. Obviously the low vapor pressure of molten KCl is helpful for it being used in a eutectic salt mixture.
The specific heat capacity of molten KCl is around Cp = 73.6 J/mol*K = 987.24 J/kg*K in the temperature range of 1044-2000 K.
3. Properties of Binary Molten Salt
This section surveyed properties of binary molten salts NaCl + AlCl3,KCl + AlCl3. The compositions mentioned in the discussion are all based on mole fractions. The covalent salts AlCl3 and ZnCl2 both have low melting point,while the ionic salts NaCl and KCl both have rather high boiling points or high temperature stability. It is thus promising that the mixture of covalent and ionic eutectic salts has the potential to possess both low melting point and good stability at high temperatures.
3.1. Mixture of NaCl + AlCl3
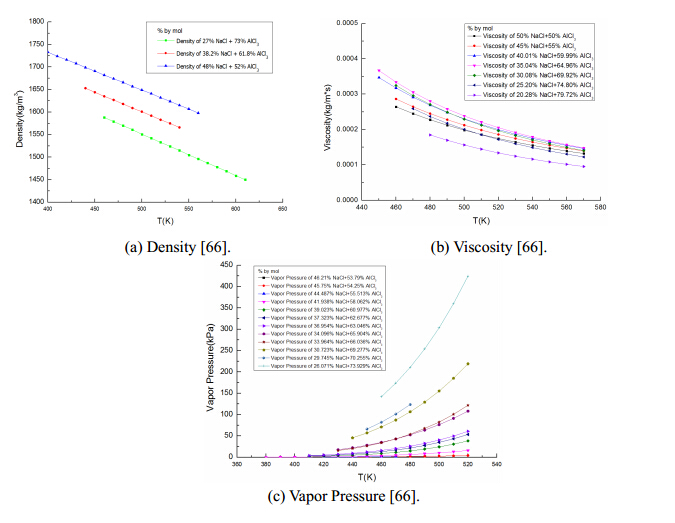
Eutectic melting pointfor NaCl + AlCl3 is generally low. For example,the mixture in a mole fraction of 36.8% NaCl + 63.2% AlCl3 has a melting point of Tm = 378-381 K(105-108 ℃)[66].
The densities of salt mixture NaCl + AlCl3 in three compositions under molten states at different temperatures are given in Table 2,which are also plotted in Figure 7(a). The more NaCl is included in the mixture,the high the densities are.
Table 2.Density of molten salt NaCl + AlCl3(% by mole) [66].
| T(K) | p(kg/m3) |
| 27% NaCl + 73% AlCl3 | 38.2% NaCl + 61.8% AlCl3 | 48% NaCl + 52% AlCl3 |
27%NaCl + 73%AlCl3: ρ=2011−0.92×T,Temperature Range: 460-610K(16)
38.2%NaCl + 61.8%AlCl3:ρ=2034−0.866×T
,Temperature Range: 440-540K(17)
48%NaCl + 52%AlCl3: ρ=2068−0.838×T,Temperature Range: 400-560K(18)
where p(kg/m3)is density and T(K)is temperature. |
| 400 | | | 1733 |
| 410 | | | 1724 |
| 420 | | | 1716 |
| 430 | | | 1708 |
| 440 | | 1653 | 1699 |
| 450 | | 1644 | 1691 |
| 460 | 1588 | 1635 | 1682 |
| 470 | 1579 | 1627 | 1674 |
| 480 | 1570 | 1618 | 1666 |
| 490 | 1561 | 1609 | 1657 |
| 500 | 1551 | 1601 | 1649 |
| 510 | 1542 | 1592 | 1641 |
| 520 | 1533 | 1583 | 1632 |
| 530 | 1524 | 1575 | 1624 |
| 540 | 1515 | 1566 | 1615 |
| 550 | 1505 | | 1607 |
| 560 | 1496 | | 1598 |
| 570 | 1487 | | |
| 580 | 1478 | | |
| 590 | 1469 | | |
| 600 | 1459 | | |
| 610 | 1450 | | |
Viscosities of molten salt mixture NaCl + AlCl3 in seven compositions are obtained from literature [66] as given in Table 3 and illustrated in Figure 7(b). The low viscosities are favorable for the eutectic molten salts being used as heat transfer fluids.
Table 3.Viscosity of liquid NaCl + AlCl3(% by mole) [66] .
| T(K) | μ(kg/m*s) |
| 50%NaCl | 45%NaCl | 40.01%NaCl | 35.04%NaCl | 30.08%NaCl | 25.20%NaCl | 20.28%NaCl |
50%NaCl + 50%AlCl3 :
μ=7.2702×10−6exp(3285.3/RT),Range : 460-570 K(19)
45%NaCl + 55%AlCl3 :
μ=6.8398×10−6exp(3413.5/RT),Range : 460-570 K(20)
40.01%NaCl + 59.99%AlCl3 :
μ=5.7828×10−6exp(3661.1/RT),Range : 450-570 K(21)
35.04%NaCl + 64.96%AlCl3 :
μ=4.9477×10−6exp(3850.2/RT),Range : 450-570 K(22)
30.08%NaCl + 69.92%AlCl3 :
μ=4.2341×10−6exp(3966.7/RT),Range : 460-570 K(23)
25.20%NaCl + 74.80%AlCl3 :
μ=3.6622×10−6exp(3977.5/RT),Range : 470-570 K(24)
20.28%NaCl + 79.72%AlCl3 :
μ=2.8309×10−6exp(3985.8/RT),Range : 480-570 K(25)
where μ(kg/m*s)is viscosity,T(K)is temperature,and R = 1.98716(cal/K*mol). |
| 50%AlCl3 | 55%AlCl3 | 59.99%AlCl3 | 64.96%AlCl3 | 69.92%AlCl3 | 74.80%AlCl3 | 79.72%AlCl3 |
| 450 | | | 0.0003469 | 0.0003667 | | | |
| 460 | 0.0002645 | 0.000286 | 0.0003174 | 0.0003339 | 0.0003246 | | |
| 470 | 0.000245 | 0.000264 | 0.0002914 | 0.0003053 | 0.000296 | 0.000259 | |
| 480 | 0.0002277 | 0.000245 | 0.0002686 | 0.0002802 | 0.0002709 | 0.000237 | 0.0001848 |
| 490 | 0.0002123 | 0.000228 | 0.0002483 | 0.000258 | 0.0002489 | 0.0002177 | 0.0001697 |
| 500 | 0.0001984 | 0.000212 | 0.0002304 | 0.0002384 | 0.0002294 | 0.0002006 | 0.0001564 |
| 510 | 0.0001859 | 0.000199 | 0.0002143 | 0.000221 | 0.0002121 | 0.0001854 | 0.0001445 |
| 520 | 0.0001747 | 0.000186 | 0.0001999 | 0.0002054 | 0.0001967 | 0.000172 | 0.000134 |
| 530 | 0.0001645 | 0.000175 | 0.000187 | 0.0001915 | 0.000183 | 0.0001599 | 0.0001246 |
| 540 | 0.0001553 | 0.000165 | 0.0001753 | 0.0001789 | 0.0001707 | 0.0001491 | 0.0001162 |
| 550 | 0.0001469 | 0.000155 | 0.0001648 | 0.0001676 | 0.0001596 | 0.0001394 | 0.0001086 |
| 560 | 0.0001392 | 0.000147 | 0.0001552 | 0.0001574 | 0.0001496 | 0.0001306 | 0.0001017 |
| 570 | 0.0001322 | 0.000139 | 0.0001465 | 0.0001481 | 0.0001405 | 0.0001227 | 0.0000955 |
There is a very limited number of data for the thermal conductivity of NaCl + AlCl3 [66]. For a mixture in mole fraction of 27%NaCl + 73%AlCl3(with a melting point of 460 K)the liquid thermal conductivity at 467 K is 0.2217 W/(m K).
V apor pressures of NaCl + AlCl3 in a dozen of different compositions are shown in Table 4 and Figure 7(c). The corresponding equations of the vapor pressures are also provided in the table.
Table 4.Vapor pressure of NaCl + AlCl3(% by mole) [66] .
| T(K) | Pvap(kPa) |
| 46.21% NaCl 53.79% AlCl3 | 45.75% NaCl 54.25% AlCl3 | 44.49% NaCl 55.51% AlCl3 | 41.94% NaCl 58.06% AlCl3 | 39.02% NaCl 60.98% AlCl3 | 37.32% NaCl 62.68% AlCl3 | 36.94% NaCl 63.06% AlCl3 | 34.10% NaCl 65.90% AlCl3 | 33.96% NaCl 66.04% AlCl3 | 30.72% NaCl 69.28% AlCl3 | 29.75% NaCl 70.25% AlCl3 | 26.07% NaCl 73.93% AlCl3 |
46.21%NaCl + 53.79%AlCl3 :
Pvap=10(4.71496−1771/T)/760×101.325,Range : 440-490K(26)
45.75%NaCl + 54.25%AlCl3 :
Pvap=10(5.94281−2304.5/T)/760×101.325,Range : 420-520K(27)
44.487%NaCl + 55.513%AlCl3 :
Pvap=10(5.77583−2177.5/T)/760×101.325,Range : 420-470K(28)
41.938%NaCl + 58.062%AlCl3 :
Pvap=10(6.72729−2416.6/T)/760×101.325,Range : 380-520K(29)
39.023%NaCl + 60.977%AlCl3:
Pvap=10(7.34912−2542.8/T)/760×101.325,Range : 410-520K(30)
37.323%NaCl + 62.677%AlCl3 :
Pvap=10(7.27205−2427.5/T)/760×101.325,Range : 410-520K(31)
36.954%NaCl + 63.046%AlCl3 :
Pvap=10(7.09260−2304.9/T)/760×101.325,Range : 410-520K(32)
34.096%NaCl + 65.904%AlCl3 :
Pvap=10(6.66296−1952.0/T)/760×101.325,Range : 430-520K(33)
33.964%NaCl + 66.036%AlCl3 :
Pvap=10(7.20848−2208.4/T)/760×101.325,Range : 430-520K(34)
30.723%NaCl + 69.277%AlCl3 :
Pvap=10(6.96901−1951.6/T)/760×101.325,Range : 440-520K(35)
29.745%NaCl + 70.255%AlCl3 :
Pvap=10(7.04376−1956.6/T)/760×101.325,Range : 450-480K(36)
26.071%NaCl + 73.929%AlCl3 :
Pvap=10(7.14703−1894.8/T)/760×101.325,Range : 460-520K(37)
where Pvap(kPa)is vapor pressure and T(K)is temperature. |
| 380 | | | | 0.311 | | | | | | | | |
| 390 | | | | 0.453 | | | | | | | | |
| 400 | | | | 0.647 | | | | | | | | |
| 410 | | | | 0.908 | 1.871 | 2.994 | 3.942 | | | | | |
| 420 | | 0.381 | 0.52 | 1.255 | 2.629 | 4.142 | 5.366 | | | | | |
| 430 | | 0.511 | 0.687 | 1.707 | 3.636 | 5.645 | 7.199 | 17.715 | 15.76 | | | |
| 440 | 0.653 | 0.676 | 0.895 | 2.29 | 4.954 | 7.585 | 9.53 | 22.465 | 20.608 | 45.547 | | |
| 450 | 0.803 | 0.884 | 1.153 | 3.033 | 6.658 | 10.058 | 12.46 | 28.19 | 26.658 | 57.151 | 66.171 | |
| 460 | 0.977 | 1.143 | 1.469 | 3.969 | 8.835 | 13.176 | 16.101 | 35.026 | 34.081 | 71.009 | 82.26 | 142.171 |
| 470 | 1.18 | 1.461 | 1.852 | 5.134 | 11.583 | 17.064 | 20.581 | 43.12 | 43.119 | 87.414 | 101.318 | 173.96 |
| 480 | 1.413 | 1.848 | | 6.57 | 15.015 | 21.861 | 26.039 | 52.626 | 54.02 | 106.681 | 123.714 | 211.076 |
| 490 | 1.681 | 2.316 | | 8.325 | 19.26 | 27.726 | 32.631 | 63.708 | 67.858 | 129.14 | | 254.098 |
| 500 | | 2.876 | | 10.447 | 24.458 | 34.83 | 40.523 | 76.536 | 82.525 | 155.139 | | 303.627 |
| 510 | | 3.541 | | 12.995 | 30.771 | 43.367 | 49.9 | 91.288 | 100.738 | 185.034 | | 360.285 |
| 520 | | 4.325 | | 16.028 | 38.373 | 53.541 | 60.955 | 108.15 | 122.03 | 219.201 | | 424.712 |
3.2. Mixture of KCl + AlCl3
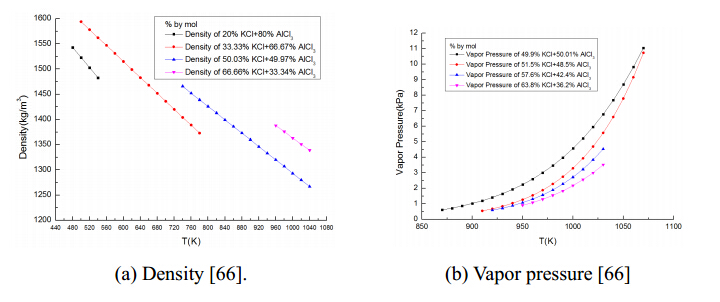
The melting point of this binary salt system is relatively low. For the mole composition of 33%KCl + 67%AlCl3 there is Tm = 401 K(128 ℃)[66]. The densities for mixtures in four different compositions at different temperatures are shown in Table 5 and drawn in Figure 8(a)[66]. Vapor pressures of the mixtures at four different compositions are shown in Table 6 and Figure 8(b)[66].
Table .5Density of liquid KCl + AlCl3(% by mole) [66] .
| T(K) | p(kg/m3) |
| 20%KCl 80%AlCl3 | 33.33%KCl 66.67%AlCl3 | 50.03%KCl 49.97%AlCl3 | 52.78%KCl 47.22%AlCl3 |
20%KCl + 80%AlCl3 :
ρ=2025.2−1.0038×T,Range : 480-540K(38)
33.33%KCl + 66.67%AlCl3 :
ρ=1988.9−0.7901×T,Range : 500-780K(39)
50.03%KCl + 49.97%AlCl3 :
ρ=1955.6−0.6622×T,Range : 740-1040K(40)
66.66%KCl + 33.34%AlCl3 :
ρ=1973.4−0.6101×T,Range : 960-1040K(41)
where
ρ(kg/m3)is density and T(K)is temperature. |
| 480 | 1543 | | | |
| 500 | 1523 | 1594 | | |
| 520 | 1503 | 1578 | | |
| 540 | 1483 | 1562 | | |
| 560 | | 1547 | | |
| 580 | | 1531 | | |
| 600 | | 1515 | | |
| 620 | | 1499 | | |
| 640 | | 1483 | | |
| 660 | | 1468 | | |
| 680 | | 1452 | | |
| 700 | | 1436 | | |
| 720 | | 1420 | | |
| 740 | | 1404 | 1466 | |
| 760 | | 1389 | 1452 | |
| 780 | | 1373 | 1439 | |
| 800 | | | 1426 | |
| 820 | | | 1413 | |
| 840 | | | 1399 | |
| 860 | | | 1386 | |
| 880 | | | 1373 | |
| 900 | | | 1360 | |
| 920 | | | 1346 | |
| 940 | | | 1333 | |
| 960 | | | 1320 | 1388 |
| 980 | | | 1307 | 1376 |
| 1000 | | | 1293 | 1363 |
| 1020 | | | 1280 | 1351 |
| 1040 | | | 1267 | 1339 |
Table .6Vapor pressure of liquid KCl + AlCl3 [66].
| T(K) | Pvap(kPa) |
| 49.9%KCl + 50.01%AlCl3 | 51.5%KCl + 48.5%AlCl3 | 57.6%KCl + 42.4%AlCl3 | 63.8%KCl + 36.2%AlCl3 |
49.9%KCl + 50.01%AlCl3:
Pvap=(107.395−5860/T)/760×101.325,Range: 870-1070K(42)
51.5%KCl + 48.5%AlCl3:
Pvap=(109.2386−7846/T)/760×101.325,Range: 910-1070K(43)
57.6%KCl + 42.4%AlCl3:
Pvap=(108.943−7634/T)/760×101.325,Range: 920-1030K(44)
63.8%KCl + 36.2%AlCl3:
Pvap=(108.4231−7212/T)/760×101.325,Range: 950-1030K(45)
where Pvap is in kPa,unit of temperature is in K. |
| 870 | 0.613 | | | |
| 880 | 0.72 | | | |
| 890 | 0.867 | | | |
| 900 | 1.027 | | | |
| 910 | 1.2 | 0.547 | | |
| 920 | 1.413 | 0.68 | 0.587 | |
| 930 | 1.653 | 0.84 | 0.72 | |
| 940 | 1.933 | 1.04 | 0.88 | |
| 950 | 2.24 | 1.267 | 1.08 | 0.907 |
| 960 | 2.6 | 1.547 | 1.307 | 1.08 |
| 970 | 3.013 | 1.88 | 1.573 | 1.293 |
| 980 | 3.466 | 2.28 | 1.893 | 1.547 |
| 990 | 3.986 | 2.746 | 2.28 | 1.827 |
| 1000 | 4.573 | 3.293 | 2.72 | 2.173 |
| 1010 | 5.226 | 3.933 | 3.226 | 2.56 |
| 1020 | 5.96 | 4.693 | 3.84 | 3 |
| 1030 | 6.773 | 5.573 | 4.533 | 3.52 |
| 1040 | 7.679 | 6.599 | | |
| 1050 | 8.693 | 7.786 | | |
| 1060 | 9.813 | 9.159 | | |
| 1070 | 11.052 | 10.732 | | |
4. Properties of Ternary Molten Salt Systems
This section surveyed properties of two ternary molten salts,NaCl + KCl + AlCl3 and NaCl + KCl + ZnCl2. All the compositions referred to are based on mole fraction.
4.1. NaCl+KCl+AlCl3
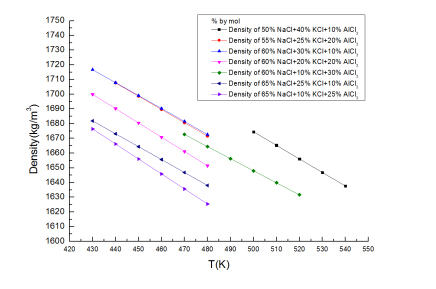
There are two eutectic points for NaCl + KCl + AlCl3 [66]. The one with a composition of 20%NaCl + 16.5%KCl + 63.5%AlCl3 has a melting point ofTm = 361.9 K(88.9 ℃). The densities of the ternary salt with different compositions at different temperatures are given in Table 7 and Figure 9. There is no vapor pressure data found for this ternary system. However,the high vapor pressure of AlCl3 could make this system to have high vapor pressures and thus not suitable as a HTF.
Table 7. Density of liquid NaCl + KCl + AlCl3(% by mole) [66] .
| T(K) | p(kg/m3) |
| 50%NaCl +40%KCl +10%AlCl3 | 55%NaCl +25%KCl +20%AlCl3 | 60%NaCl +30%KCl +10%AlCl3 | 60%NaCl +20%KCl +20%AlCl3 | 60%NaCl +10%KCl +30%AlCl3 | 65%NaCl +25%KCl +10%AlCl3 | 65%NaCl +10%KCl +25%AlCl3 |
50%NaCl+40%KCl+10%AlCl3:
ρ=2136−0.923×T,for T(K)in 500-540K(46)
55%NaCl+25%KCl+20%AlCl3:
ρ=2105−0.903×T,for T(K)in 440-480K(47)
60%NaCl+30%KCl+10%AlCl3:
ρ=2096−0.882×T,for T(K)in 430-480K(48)
60%NaCl+20%KCl+20%AlCl3:
ρ=2117−0.97×T,for T(K)in 430-480K(49)
60%NaCl+10%KCl+30%AlCl3:
ρ=2059−0.822×T,for T(K)in 470-520K(50)
65%NaCl+25%KCl+10%AlCl3:
ρ=2059−0.877×T,for T(K)in 430-480K(51)
65%NaCl+10%KCl+25%AlCl3:
ρ=2115−1.02×T,for T(K)in 960-1170K(52)
where unit of density is p(kg/m3) and T is in(K). |
| 430 | | | 1716.7 | 1699.9 | | 1681.9 | 1676.4 |
| 440 | | 1707.7 | 1707.9 | 1690.2 | | 1673.1 | 1666.2 |
| 450 | | 1698.7 | 1699.1 | 1680.5 | | 1664.4 | 1656.0 |
| 460 | | 1689.6 | 1690.3 | 1670.8 | | 1655.6 | 1645.8 |
| 470 | | 1680.6 | 1681.5 | 1661.1 | 1672.7 | 1646.8 | 1635.6 |
| 480 | | 1671.6 | 1672.6 | 1651.4 | 1664.4 | 1638.0 | 1625.4 |
| 490 | | | | | 1656.2 | | |
| 500 | 1674.5 | | | | 1648.0 | | |
| 510 | 1665.3 | | | | 1639.8 | | |
| 520 | 1656.0 | | | | 1631.6 | | |
| 530 | 1646.8 | | | | | | |
| 540 | 1637.6 | | | | | | |
4.2. NaCl + KCl + ZnCl2
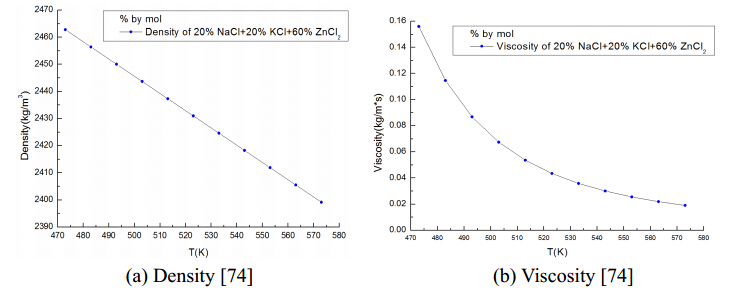
There are three eutectic mixtures for this ternary system that may have melting temperatures below 250 ℃. One particular composition is 20% NaCl + 20% KCl + 60% ZnCl2 that has a melting point of Tm = 476 K(203 ℃). Because of the relatively low vapor pressure of ZnCl2,this eutectic salt may also have a low vapor pressure and thus is very promising to be a HTF. The densities of this eutectic mixture are given in Table 8 and Figure 10(a). Viscosities of the salt are given in Table 9 and Figure 10(b).
Table 8. Densities of the molten salt 20%NaCl + 20%KCl + 60%ZnCl2 (% by mole) [74]
| T(K) | p(g/cm3) | p(kg/m3) |
| ρ=2.59−6.36×10−4(T−273); where the units are p(kg/m3),and T(K),in the range of 473-573K.(53) |
| 473 | 2.46 | 2462.8 |
| 483 | 2.46 | 2456.44 |
| 493 | 2.45 | 2450.08 |
| 503 | 2.44 | 2443.72 |
| 513 | 2.44 | 2437.36 |
| 523 | 2.43 | 2431 |
| 533 | 2.42 | 2424.64 |
| 543 | 2.42 | 2418.28 |
| 553 | 2.41 | 2411.92 |
| 563 | 2.41 | 2405.56 |
| 573 | 2.4 | 2399.2 |
Table 9. Viscosity of the molten salt 20%NaCl + 20%KCl + 60%ZnCl2 (% by mole) [74]
| T(K) | μ(cp) | μ(kg/m*s) |
| μ=1.23×10−2√Texp(1.21×103T−283); where the units areμ(cp),and T(K),within the range of 473-573K.(54) |
| 473 | 155.9932 | 0.15599 |
| 483 | 114.6464 | 0.11465 |
| 493 | 86.8344 | 0.08683 |
| 503 | 67.5008 | 0.0675 |
| 513 | 53.6699 | 0.05367 |
| 523 | 43.5235 | 0.04352 |
| 533 | 35.9132 | 0.03591 |
| 543 | 30.0916 | 0.03009 |
| 553 | 25.5594 | 0.02556 |
| 563 | 21.9752 | 0.02198 |
| 573 | 19.1002 | 0.0191 |
5. Conclusion and Outlook
This paper gave a brief introduction to the currently available high temperature HTFs and the necessity of developing new-generation materials for even higher working temperatures(at least 800 ℃)for the goal of high thermal efficiency in concentrated solar thermal power plant.
The authors particularly gave attention to possible mixtures of ionic and covalent halide salts for the potential of creating a eutectic salts to meet the basic criteria for a HTF. Low cost and almost unlimited reserve of halide salts is also important due to the large dem and in industry. The reviewing has found that some binary and ternary halide salts could have eutectic mixtures with low melting points,which therefore are recommendable for the components of a HTF.
For those halide salts recommended as the components of mixture eutectic molten salts,available properties of the individual c and idate and binary and ternary mixtures are surveyed and presented for reference of further studying and investigation of all the properties that remaining unknown so far. Table 10 summaries the availability of results obtained from literature. Some key conclusions from the survey are drawn:
(1)It is understood that the three covalent halide salts AlCl3,ZnCl2,and FeCl3 have relatively low melting points which may contribute to the low eutectic melting point for a mixture of ionic and covalent halide salts. However,the relatively very high vapor pressures of AlCl3 and FeCl3 are of concerns to the possible high vapor pressures of eutectic salt mixtures.
(2)Two binary eutectics salts NaCl-AlCl3 and KCl-AlCl3 show low eutectic melting points below 250 ℃. The system of NaCl-AlCl3 still has rather high vapor pressure which may come from the high vapor pressure of AlCl3. However,the eutectic of KCl-AlCl3 show relatively lower vapor pressure compared to that of NaCl-AlCl3. This is an indication that KCl is an important component to suppress the vapor pressure of eutectic mixtures. The viscosities of these two binary systems are low and very favorable.
(3)Two ternary eutectic salts from the system of NaCl-KCl-AlCl3 and NaCl-KCl-ZnCl2 showed low viscosities that are very favorable for heat transfer fluids. The densities of the two eutectic salts are also acceptable. However,there are no other thermal and transport properties,which need research and investigation.
Last but not least,the chemical corrosion of the surveyed salts to metals of pipes and containers is a very important issue. A detailed survey is yet to be carried out. However,one recent article [75] showed results of corrosion of Hastelloys in 13.4NaCl-33.7KCl-52.9ZnCl2(mol%)eutectic system. Evaluated from both electrochemical method and immersion test,the type N Hastelloy showed a higher corrosion rate of > 150 µm per year at 500 ℃,but the Hastelloy C-276 exhibited the lowest corrosion rate of 40 µm per year at 500 ℃. More results on corrosions of these salts to metals are expected to see in the future.
Referring to the available properties for these halide salts,the researchers teamed-up from the University of Arizona,Georgia Institute of Technology,and Arizona State University have been investigating details of properties of ternary salt systems(KCl-NaCl-AlCl3),(KCl-NaCl-ZnCl2),and (KCl-NaCl-FeCl3),as well as quaternary systems. Simulations and fast screening method are applied for searching eutectic salt compositions; while experimental tests are followed up to measure all the properties,including corrosion to metals,for evaluation of the suitability for a HTF.
Table 10. Summary of the availability of physical properties of AlCl3,ZnCl2,FeCl3,NaCl,KCl,and their mixtures.
| | Single Molten Salt | Binary Molten Salt | Ternary Molten Salt |
| AlCl3 | ZnCl2 | FeCl3 | NaCl | KCl | NaCl+AlCl3 | KCl+AlCl3 | NaCl+KCl | NaCl+KCl +AlCl3 | NaCl+KCl +ZnCl2 |
| √ : Data obtained from literature;× : No data available from literature |
| Density | √ | √ | × | √ | √ | √ | √ | √ | √ | √ |
| Viscosity | √ | √ | × | √ | √ | √ | × | √ | × | √ |
| Thermal Conductivity | × | × | × | √ | √ | × | × | × | × | × |
| Specific Heat Capacity | √ | √ | √ | √ | √ | × | × | × | × | × |
| Vapor Pressure | √ | √ | √ | √ | √ | √ | √ | √ | × | × |
| Melting Point | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
Acknowledgement
The support from the U.S. Office of DOE under the Contract DE-EE0005942 is gratefully acknowledged.
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: