1.
Introduction
Dengue fever is a rapidly spreading mosquito-borne disease all over the world, and dengue virus (DENV) is transmitted to human by Aedes (stegomyia) mosquito, a genus of mosquitoes. Aedes aegypti and Aedes albopictus are the vectors for transmitting dengue virus [1], and dengue fever can be triggered by dengue virus serotypes: DENV-1, DENV-2, DENV-3, DENV-4 [2,3]. When human infects the DENV, the symptoms of illness can range from mild forms such as a sudden onset of fever, headache, myalgia and a skin erythema [4], to severe forms including dengue hemorrhagic fever (DHF) and dengue shock syndrome (DSS) [5]. Since severe outbreaks of dengue fever in the 1950s in Philippines and Tahiland, it has spread throughout the Africa, Southeast Asia, Western Pacific Region, South America and Eastern Mediterranean Region, which leads to roughly 12,500 to 25,000 deaths each year [6,7].
According to the World Health Organization (WHO), about 50–100 million dengue cases are reported every year over 100 countries [7,8], and more than 2.5 billion people meet the risk of dengue virus transmission. There are very serious infection of dengue fever in Guangdong province, China [9]. It has been reported that there were 45230 dengue cases in Guangdong Province in 2014, which is a big outbreak of dengue fever in Guangdong. In recent decades, dengue fever has leaded a serious health and social problem in the world, and it has turned into a worldwide public health problem.
Mathematical models are used to study the transmission dynamics of dengue fever. It is the first time that Esteva et al. [10] proposed a dengue model and established the global stability of the endemic equilibrium. Later on, they analyzed the effect of mechanical and vertical transmission on the transmission dynamics of dengue virus in [11]. Chowell et al. [12] evaluated the basic reproduction number of dengue with data, and Khan et al. [13] studied a single-strain dengue model and the basic reproduction number was analyzed. Tewa et al. [14] developed the single-strain dengue model and proved the global stability of the equilibria. Yang and Ferreira [15] assessed the effect of vector control on dengue virus transmission, and obtained that the dengue fever can be eradicated if mosquito population dies out. Garba et al. [16] studied the backward bifurcation in dengue virus transmission model, and revealed that the implement of an imperfect vaccine could result in the effective control of dengue in a community provided that the vaccine efficacy and vaccine coverage are high enough. Abdelrazec et al. [17] investigated the effect of available resources of health system on the spread and control of dengue fever. Although a few studies have explored the dynamics of dengue virus transmission, there are few work addressing on the effect of climatic factors on dengue virus transmission.
Transmission of dengue virus is greatly influenced by temperature and precipitation [18,19]. Rueda et al. [20] showed that circadian rhythm of mosquito population is hugely affected by temperature and rainfall. Tun-Lin et al. [21] studied the impact of temperature on maturation period of mosquitoes, and they showed that the duration of development from egg to adult is closely related to temperature through the experiment methods, and found that higher temperature can shorten the duration of virus replication and increase mosquito reproduction and contacts with human [22]. Fan et al. [23] analyzed a delay differential equation model, and explored the effect of temperature on the mosquito abundance. Li et al. [24] explored the driving force of the dengue outbreak in Guangdong province in 2014 through a seasonally-driven model. Bai et al. [25] studied the effect of of climate change on the transmission of mosquito-borne diseases in China, and found that global warming extends the land area suitable for vector mosquitoes, and expands distribution of dengue. Therefore, it is necessary and important to study the effect of precipitation and temperature on the transmission of dengue virus.
In this paper, we propose a dengue model with maturation delay for mosquito production, where the birth rate and biting rate of mosquitoes depend on the average temperature. The basic reproduction number is computed by the next generation matrix. We prove the global stability of the disease-free steady state and uniform persistence of the system which are determined entirely by the basic reproduction number. Furthermore, we investigate the outbreak of dengue in Guangdong Province in 2014 through our model and data.
This paper is organized as follows. In section 2, we formulate a dengue virus transmission model, and compute the basic reproduction number R0. In section 3, the dynamics of the dengue model are completely determined by the basic reproduction number R0. If R0<1, the disease-free steady state is globally asymptotically stable and dengue fever dies out; if R0>1, there is at least one positive periodic solution and dengue fever persists. Section 4 provides a case study on dengue fever in Guangdong to illustrate our results which can be applied to other mosquito-borne diseases. Finally, a brief discussion completes the paper.
2.
Model formulation
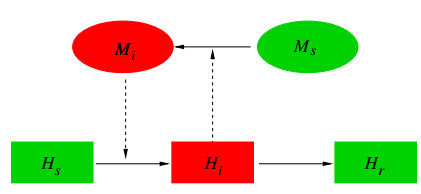
The mosquito population Nm(t) is divided into two compartments: The susceptible female adult mosquitoes Ms(t) and the infectious female adult mosquitoes Mi(t). Let Nm(t)=Ms(t)+Mi(t) represent the total number of female adult mosquitoes. Here we ignore the recovered class of mosquitoes, because a mosquito never recovers from the infection in the short life span [26]. Let Nh(t) denote the number of the total human population at time t, which is composed of the number of susceptible individuals Hs(t), the number of infectious individuals Hi(t), and the number of recovered individuals Hr(t). Then Nh(t)=Hs(t)+Hi(t)+Hr(t). The flow chart (Figure 1) depicts the transmission cycle of dengue virus between mosquitoes and humans.
Based on the above assumptions, and extending the ideas in [23,27,28,29,30], our dengue virus transmission model can be written as
where all parameters are positive, and rm(t) and k(t) are positive, continuous ω-periodic functions with ω=12 months. Due to the density dependence of mosquito development from egg to adult, a Ricker type function is chosen as the birth rate of mosquitoes [29,31,32]. Let τ be the maturation period of mosquitoes, and rm is the intrinsic oviposition rate, and dj is the death rate of juvenile mosquitoes. We assume that dm is the natural death rate of adult female mosquitoes, and dh is the natural death rate of humans. Then rm(t)Nm(t−τ) denotes the number of mosquito's eggs laid τ units ago, and e−djτ denotes the survival probability during immature stages. Let k(t) be the per capita biting rate of mosquitoes on humans, and βm(resp. βh) represents the transmission probability from an infectious human to a susceptible mosquito (resp. from an infectious mosquito to a susceptible human). Since the birth rate rm(t) depending on the temperature affects the demographic of vector mosquitoes, and biting rate k(t) depending on the temperature influences the virus transmission between humans and mosquitoes, then we assume that rm(t) and k(t) are ω-periodic functions. The parameter rh is the recruitment rate of human and μh denotes the recovery rate of the infectious human.
It follows from model (2.1) that the mosquito population Nm(t)=Ms(t)+Mi(t) contents the following equation:
From [33,34,35], we know that there exists a globally asymptotically stable positive ω-periodic solution N∗m(t) in model (2.1). In this paper, we consider the dengue virus transmission model with periodic environment. Then we assume
(H) A function rm(t) is periodic in C1(R+) with period ω, and then we can choose a l0>0 which gives rm(t)e−djτe−αL−dmL<0,∀L>l0. Besides, there is a globally asymptotically stable positive ω-periodic solution N∗m(t) in C([−τ,0],R+)∖{0} for model (2.1).
Thus, the following results are established.
Theorem 2.1. For ∀ϕ∈C([−τ,0],R5+), there is a unique nonnegative solution of model (2.1) through ϕ, and all solutions of model (2.1) are uniformly bounded and ultimately bounded.
Proof. For ∀ϕ∈C([−τ,0],R5+), we denote f(t,ϕ):=
For ∀ϕ∈C([−τ,0],R5+), it is clear that f(t,ϕ) is continuous and Lipschitzian with respect to ϕ. Then model (2.1) has a unique solution through (0,ϕ). Since fi(t,φ)≥0 for φ≥0 and φi(0)=0, then C([−τ,0],R5+) is positively invariant set (see Remark 5.2.1 in [36]).
For human population Nh(t),
It follows from the comparison principle that the solution of model (2.1) always exists for any time t≥0. In addition,
and
ensure that all solutions are ultimately bounded. Besides, when Nh(t)≥max{l0,rh/dh} and Nv(t)≥max{l0,rh/dh}, the inequalities
hold, which means that all solutions of model (2.1) are uniformly bounded.
For system (2.1), there always exist the trivial equilibrium (0,0,N∗h,0,0) and disease-free state (N∗m(t),0,N∗h,0,0), where N∗h=rh/dh and N∗m(t) is the positive periodic solution of model (2.2). For the trivial equilibrium, the disease is not transmitted when there is no mosquito, and then trivial equilibrium (0,0,N∗h,0,0) will not be studied in this paper. Using the theory in [34], we compute the basic reproduction number of model (2.1). Linearizing model (2.1) at the disease-free periodic state (N∗m(t),0,N∗h,0,0), we have
Denote
and
Then model (2.3) becomes
with x(t)=(Mi(t),Hi(t),Hr(t))T.
For periodic system
Y(t,s)(t≥s) represents the evolution operator. Then we have
For all ω−periodic functions from R to R5, we define the Banach space Cω and initial distribution of infectious mosquitoes and humans. Then the rate of new infectious mosquitoes and humans is F(s)ϕ(s), where s is the time for infected mosquitoes and humans introduced. The distribution of infected individuals is Y(t,s)F(s)ϕ(s), where those infected mosquitoes and humans were infected at time s and stay the infected classes at time t≥s. Therefore, the distribution of accumulative new infectious mosquitoes and humans at time t produced by infected mosquitoes and humans ϕ(s) brought at the previous time is
Linear operator G:Gω→Gω satisfies
Denote ρ(G) as the spectral radius of G. According to [34], we obtain the next generation operator G and R0=ρ(G) is the basic reproduction number.
For system
we know that W(t,λ) is the monodromy matrix and parameter λ>0. Obviously, −V(t) is cooperative and F(t) is nonnegative, and then for λ>0, ρ(W(ω,λ)) is continuous and nonincreasing and limλ→∞ρ(W(ω,λ))<1. It follows from Theorem 2.1 in [34] that we have the following results.
Lemma 2.2. For the basic reproduction number, we have the following results:
(I) If there is λ0>0 for ρ(W(ω,λ))=1, then λ0 is an eigenvalue of G and R0>0.
(II) If R0>0, then ρ(W(ω,λ))=1 has a unique solution λ=R0
(III) R0=0 if and only if ρ(W(ω,λ))<1, ∀λ>0.
The Lemma 2.2 can be applied to compute the basic reproduction number R0 by numerical simulations ensures that R0 is in scale with k(t).
3.
Threshold dynamics
In this section, we prove the global asymptotically stability of the disease-free periodic state when R0<1 and the uniform persistence of system (2.1) when R0>1.
Define
and
Obviously, X0 is an open set. Suppose that (2.1) has an unique solution u(t,ϕ) with u0(ϕ)=ϕ and Φ(t)φ=ut(φ). In addition, we assume that P:X→X is the Poincaré map corresponding to the model (2.1).
3.1. Global stability of the disease-free periodic state
It follows from Theorem 2.2 in [34] that the disease-free periodic state is locally stable if R0<1 and unstable if R0>1. Let XK=C([−τ,0],[0,K]5) for some K≥max{l0,rh/dh}. Then we will show that the disease dies out when R0<1.
Theorem 3.1. If R0<1 and (H) holds, then the disease-free periodic state of model (2.1) is globally asymptotically stable in C([−τ,0],R5+)∖{(0,0,N∗(h),0,0}.
Proof. It follows from Theorem 2.1 that XK is positively invariant. Then
Denote
From Theorem 2.2 in [34], R0<1 if and only if ρ(ΦF−V(ω))<1. Since that the solutions are continuous in σ, then limσ→0+ΦMσ(ω)=ΦF−V(ω). Besides, we know that the spectrum for matrices is continuous [37], which implies that limσ→0+ρ(ΦMσ(ω))=ρ(ΦF−V(ω)). Therefore, we have ρ(ΦMσ(ω))<1 for some σ. From mosquito and human population, there is a T1=T(σ) such that
Subsequently, we obtain
Using the Lemma 2.1 in [38], we obtain a positive ω-periodic function ℏ(t) satisfying that h′(t)=Mσ(t)h(t) has a solution h(t)=eθtℏ(t) and θ=1ωlnρ(ΦMσ(ω))<0. The boundedness of the positive ω-periodic function ℏ(t) implies that limt→∞h(t)→0. Applying the comparison principle in [36], we obtain that Mi(t)→0,Hi(t)→0 and Hr(t)→0 as t→∞. The theory of asymptotically periodic semiflow [39] gives that Ms(t)→N∗m(t) and Hs(t)→N∗h as t→∞. Therefore, the disease-free periodic state of model (2.1) is globally asymptotically stable in C([−τ,0],R5+)∖{(0,0,N∗h,0,0} when R0<1.
3.2. Uniform persistence when R0>1
In this section, we show the uniform persistence of the disease when R0>1.
Theorem 3.2. When the assumption (H) holds and R0>1, there exists an ε>0 such that any solution of the system (2.1) in C([−τ,0],R5+) with Mi(0)>0,Hi(0)>0 and Hr(0)>0 satisfies
In addition, system (2.1) has at least one positive periodic solution.
Proof. Since P:X→X is the Poincaré map corresponding to system (2.1), then P(ϕ)=uω(ϕ),∀ϕ∈X, and then Φ(t)(X0)⊂X0,∀t≥0. From Theorem 2.1, we obtain that Pn0 is compact for all n0ω>τ and P is point dissipative. According to the Theorem 2.9 in [40], P generates a global attractor which is denoted as A.
Denote E1={(0,0,N∗h,0,0)} and E2={(N∗m0,0,N∗h,0,0)}, where N∗m0(θ)=N∗m(θ),∀θ∈[−τ,0]. There exists an δ0>0 such that inft≥0N∗m(t)>2δ0. limϕ→E1(Φ(t)ϕ−E1)=0 uniformly for t∈[0,ω] gives that we can choose an δ1 such that
We claim that
Suppose not, then there are some ϕ∈X0 such that lim supn→∞‖Φ(nω)φ−E1‖<δ1. Thus we choose an T2≥1 such that ‖Φ(t)φ−E1‖<δ1,∀n≥T2. For t−τ≥T2ω, t=nω+ˉt, n≥T2,ˉt∈[0,ω] and ‖Φ(t)φ−E1‖=‖Φ(ˉt)Φ(nω)φ−E1‖≤δ0 hold. Then Ms(t)≤δ0,Mi(t)≤δ0 and Nm(t)≤δ0 for t−τ≥T2ω. Nm(0)=φ1(0)+φ2(0) implies that limt→∞(Nm(t)−N∗m(t))=0, which is a contradiction with inft≥0N∗m(t)>2δ0.
Denote
Using the same discussion in Theorem 3.1, there is an σ1>0 such that ρ(ΦˉMσ(ω))>1,∀σ∈[0,σ1]. limϕ→E2(Φ(t)ϕ−Φ(t)E2)=0 uniformly for t∈[0,ω] implies that we can choose an ε1 such that
The we claim that
Suppose not, then there are some φ∈X0 satisfying lim supn→∞‖Φ(nω)φ−E2‖<ε1. We choose an T3≥1 such that ‖Φ(nω)φ−E2‖<ε1,∀n≥T3. For t−τ≥T3ω,t=nω+ˉt,n≥T3,ˉt∈[0,ω], then ‖Φ(t)φ−Φ(t)E2‖=‖Φ(ˉt)Φ(nω)φ−Φ(ˉt)Φ(nω)E2‖=‖Φ(ˉt)Φ(nω)φ−Φ(ˉt)E2‖, and
Lemma 2.1 in [38] implies that ˉh(t)=eθtℏ(t) is a solution of equation ˉh′(t)=Mσ(t)ˉh(t) for ℏ(t) with period ω, where θ=1ωlnρ(ΦMσ(ω))>0. The boundedness of the positive ω−periodic function ℏ(t) gives that limt→∞ˉh(t)→+∞. From Φ(t)φ∈X0,∀t≥0, we can choose an T0≥T3 and ˉε such that
The comparison principle [36] ensures that
Then limt→∞|(Mi(t),Hi(t),Hr(t))|=∞, which is a contradiction with Theorem 2.1.
Denote
Next we prove that M∂=M1∪M2. ui(t,φ)=0, ∀φ∈M2, i=1,2. Then M2⊂M∂. For ∀φ∈M1, Z(t)∈(R+,R5+) ensures that Zi(t)=0,∀t≥0 for i=2,4,5. Then
where Z1(0)=φ1(0). Assume that Z3(t) satisfies
Then system (2.1) through φ has a solution Z(t). The uniqueness of solution implies that u(t,φ)=Z1(t),∀t≥0 and M1⊂M∂. Therefore, M1∪M2⊂M∂. Next, we will prove M∂⊂M1∪M2. Since ∑2j=1φj(0)>0 for ∀φ∈∂X0∖(M1∪M2), then limt→∞|∑2j=1uj(t,φ)−N∗m(t)|=0. We can choose an t0>0 such that u1(t,φ)>0,∀t>t0. Clearly, u3(t,φ)>0,∀t>0. If φ2(0)>0, then uj(t,φ)>0 for i∈{2,4,5},∀t>0. Furthermore, if φ4(0)>0, then u2(t,φ)>0,∀t>t0. Therefore, u(t,φ)∈X0,∀t>t0, which means that ∀φ∈∂X0∖(M1∪M2). There are some nω>t0 such that Pn(φ)∉∂X0, and then M∂⊂M1∪M2. Based on the above discussions, we obtain that for P∈M∂, E1 and E2 are disjoint, compact and isolated invariant sets, and then ˉAM∂=⋃ϕ∈M∂ω(ϕ)={E1,E2}. Besides, there is no cycle in M∂ for subset of {E1,E2}. Therefore, for P∈X, E1 and E2 are isolated invariant sets and Ws(Ei)∪X0=∅(i=1,2), where Ws(Ei) is the stable set of Ei. Note that acyclicity theorem on uniform persistence [39] gives the uniform persistence of P and periodic semiflow Φ(t). According to Theorem 4.5 in [40], we obtain that there is an ω−periodic solution Φ(t)ϕ∗ with ϕ∗∈X0 in model (2.1).
Using Theorem 4.5 in [40] with ρ(x)=d(x,∂X0), we have that there is a compact global attractor A0 for P:X0→X0, and A0=P(A0)=Φ(ω)A0 ensures that φi(0)>0 for i=2,4,5, which means that ϕi(0)>0 for i=1,3 due to the invariance of A0. Denote D0=⋃t∈[0,ω]Φ(t)A0, then φi(0)>0,∀φ∈D0,i=1,2. Also, D0⊂X0 and limt→∞d(Φ(t)ϕ,D0)=0,∀ϕ∈X0. We define q:X→R+ with q(ϕ)=min1≤i≤5{ϕi(0)},∀ϕ∈X which is continuous. The compactness of D0∈X0 implies that infϕ∈D0q(ϕ)=minϕ∈D0q(ϕ)>0. Then we can choose an ε>0 such that
In addition, lim inft→∞min(Φ(t)ϕ∗)≥ε, and then ui(t,ϕ∗)>0,1≤i≤5,∀t≥0. Consequently, system (2.1) has at least one positive periodic solution u(t,ϕ∗).
When the basic reproduction number is greater than one, the disease persists in both mosquito and human population, and there has always infected mosquitoes and humans if they exist at the initial moment. In addition, periodic oscillations appear in both mosquito and human population.
4.
A case study
In this section, we study the outbreak of dengue fever in Guangdong Province, China in 2014. We verify our theretical results and explore the effect of maturation delay on the dengue virus transmission. The simulations are implemented by Matlab software.
China is hit by the outbreak of dengue fever since 1978, and then it spreads over Southern regions. There are serious infections of dengue in Guangdong after 1997 [9]. Cumulative number of reported cases of Guangdong province accounts for 94.99% of the total reported cases in China, and all death cases are in Guangdong Province. Especially in 2014, Guangdong Province suffered from the worst dengue outbreak. This can be reflected by reported dengue fever cases in Guangzhou city. To carry out numerical simulations on the seasonal transmission pattern in Guangdong Province, parameter values will be estimated in model (2.1).
4.1. Parameter estimates
From the National Bureau of Statistics of China in 2010, the number of people in Guangdong Province is 104,410,000. Here we assume that all people in Guangdong Province are susceptible. The average life expectancy of Chinese people was 74.83 years in 2010, and then the natural death rate of human is dh=174.83×12=0.001114 Month−1. Hence, the recruitment rate rh of human for Guangdong province can be calculated by rh=dh×104410000=116313. The details of parameters are shown in Table 1.
Using the monthly mean temperature (National Centers for Environmental Information) observed in six monitoring stations in Guangdong Province from January 2003 to December 2012, we can calculate the average monthly temperature for Guangdong Province which is shown in Table 2. By the relationship between temperature, recruitment rate and biting pattern, we can estimate the parameters rm(t) and k(t).
Based on the experiments in [44] on Aedes aegypti mosquitoes over the range of 10.54∘C, we choose the expressions of the intrinsic oviposition rate
where C is the temperature in Celsius. In order to make sure the positivity of the intrinsic oviposition rate, we choose C≥12∘C. The intrinsic oviposition rate is zero when C<12∘C. The intrinsic oviposition rate in Guangdong Province can be fitted by
The best fitted curve for the duration of the mosquito gonotrophic cycle is given by
Therefore, the temperature-dependent contact rate per unit time in Guangdong Province can be written as
We fit the biting rate in Guangdong province, and then we have
4.2. Model validation
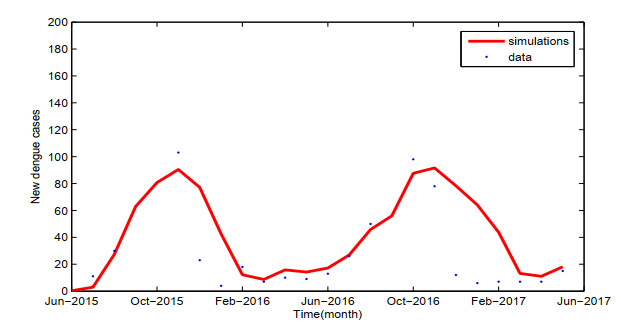
In this subsection, we use MATLAB software to simulate the dengue virus transmission in Guangdong Province based on the data from the Health Department of Guangdong Province, and obtain the monthly numbers of newly reported dengue cases from June 2015 to May 2017. The initial values are chosen as Ms(0)=241280,Mi(0)=300,Hs(0)=10000,Hi(0)=15000 and Hr(0)=98139900. We take June 1 as the starting point. The simulations from June 2015 to May 2017 are presented in Figure 2 which shows the comparison between the monthly reported dengue cases and the model predicting cases for Guangdong Province. Our simulations are in accordance with the dengue cases reported in Guangdong Province.
4.3. Long term behaviors
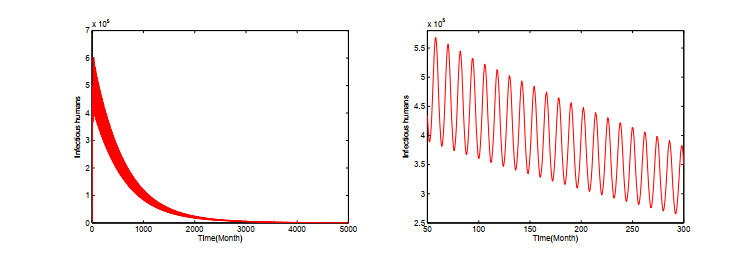
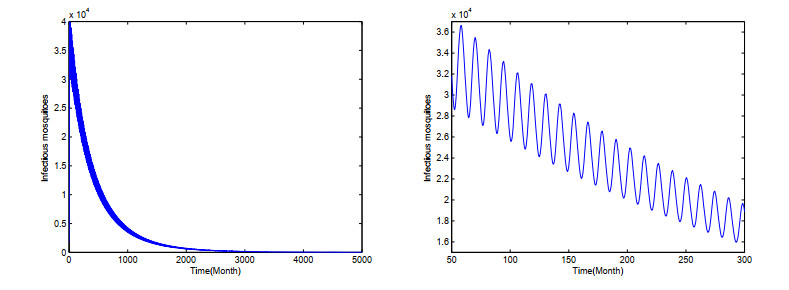
In this subsection, we show the long term behaviors of dengue virus transmission in Guangdong Province. Setting Ms(θ)=24120,Mi(θ)=1800,Hs(θ)=3000,Hi(θ)=150,Hr(θ)=30 for all θ∈[−τ,0]. Firstly, we choose βm=0.75,βh=0.75,α=0.0001,dh=0.001114,rh=116313,dm=0.07,dj=0.46,τ=0.8224,μ=0.1428. Using Matlab software and Lemma 2.2, we get the basic reproduction number R0=0.9981<1. In this case, it follows from Figures 3 and 4 that both infectious human and infectious mosquito approach to zero eventually, which means that the dengue fever dies out. This demonstrates the theoretical results in Theorem 3.1.
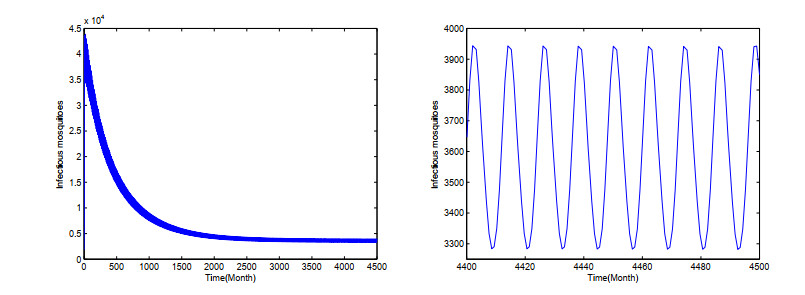
Similarly, we take dm=0.06,dj=0.4, τ=0.3947, and all other parameters are the same as these in Figures 3 and 4. We can get R0=1.1296>1. In this case, it follows from Figures 5 and 6 that a positive periodic solution is observed and the dengue fever persists uniformly. The periodic fluctuations of the infectious humans (resp. mosquitoes) compartments are shown in Figure 5 (resp. Figure 6). Numerical simulations demonstrate that our simulations are consistent with the Theorem 3.2.
5.
Discussions and conclusions
Climatic factors contribute to the dengue virus transmission. Scientific evidences have shown that higher temperature will increase the proportion of infected mosquitoes, which is dangerous for human [45]. Hale et al. [18,46] found that climate change could increase the risk of dengue virus transmission, and about half of the global population will suffer from the risk of dengue infection in 2085 if the climate gets worse. Thus it is reasonable to study the impact of climatic factors such as temperature on dengue virus transmission.
Mathematical models can offer us an important method to explore the transmission and risk of dengue virus and help us to control the disease in time-varying environments. In this paper, a dengue model with maturation delay and seasonality is formulated to study the impact of temperature on the transmission of dengue virus, where the birth rate and biting rate of mosquitoes depend on the average temperature. This model gives a baseline against that climate change can be estimated in the long term. Applying the methods in [34], we have figured out the basic reproduction number R0. From the theoretical point of view, the disease-free periodic state E0 is globally asymptotically stable when R0<1, which means that the infection can be cleared from the population if there is a small invasion. System admits at least one positive periodic solution when R0>1, that is, the dengue fever will persist and show seasonal fluctuations (Figures 5 and 6). For our model, we chose seasonable parameter values for modeling dengue fever cases in Guangdong province in China. The basic reproduction number of the model is computed numerically. For the period of June 2016 to May 2017, since R0=0.9981<1, then the disease will be cleared out eventually in Guangdong province (Figures 3 and 4), which is consistent with the data reported from June 2016 to May 2017.
If we only consider the delay effect and assume that mosquito growth rate rm(t) and biting rate k(t) are time-independent, then the total mosquito population satisfies
For scalar Eq (5.1), it has been proven by Fan et al. [23] that Nm(t)=0 is globally asymptotically stable if rme−djτ≤dm, and Nm(t)=1αln(rmdmedjτ) is globally asymptotically stable if rme−djτ>dm. Therefore, the total mosquito population will not oscillate for any τ>0. For the full system (2.1), Eq (5.1) and the last four equations of system (2.1) are decoupled. Notice that the standard incidence rate and linear death rate are adopted in system (2.1). It has been proven by Shan et al. [47] that such incidence interaction and linear death will not generate oscillations. Hence, the delay alone will not induce any periodicity in our system.
In the present work, we only consider maturation delay as a constant, it should be more reasonable to consider maturation delay τ as a time-dependent function [48,49]. In fact, there are four development stages during a mosquito's lifetime which are egg, larva, pupa and adult. The dynamics of the first three aquatic stages have great impact on the spread of mosquito-borne diseases, and it will be more interesting to develop a structured dengue model with seasonality. We can also consider some effective measures to prevent and control the spread of dengue. These problems are left as our future work.
Our results will help us to understand dengue virus transmission between human and mosquitoes, and also be applied to other mosquito-borne disease such as West Nile virus, Zika and Chikungunya.
Acknowledgments
The authors thank the handling editor and anonymous referee for their very valuable suggestions, which greatly improve the manuscript. The research of H. Song was supported by the National Natural Science Foundation of China (11601291), and Program for the Outstanding Innovative Teams (OIT) of Higher Learning Institutions of Shanxi, and Shanxi Scholarship Council of China and Scientific and Technological Innovation Programs (STIP) of Higher Education Institutions in Shanxi. The research of C. Shan was supported by the Simons Foundation-Mathematics and Physical Sciences 523360.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: