1.
Introduction
One of the fundamental concerns of physiology is the function of ion channels. Ion channels are approximately cylindrical, hollow proteins with a hole down their middle that provides a controllable path for electrodiffusion of ions (mainly Na+, K+, Ca++ and Cl−) through biological membranes, establishing communications among cells and the external environment. This way, ion channels control a wide range of biological functions. The study of ion channels consists of two related major topics: Structures of ion channels and ionic flow properties. With a given structure of an open channel, the main interest is to understand its electrodiffusion property.
Beyond general electrodiffusion phenomema for electrolytic solutions in bulks or near charged walls, ionic flows through ion channels have more specifics, that is, the study of ionic flows has to take into considerations of global constraints, including boundary conditions in addition to the structure of an ion channel. As already demonstrated by the celebrated works [51,52,53,54,55] of Hodgkin and Huxley for neurons consisting of a population of ion channels and by works in the volume Single-Channel Recording [94] (edited by B. Sakmann and E. Neher) and many works afterwards, the properties of ion channels depend in an extremely rich way on different regions of boundary concentrations and boundary electric potentials. It is the global constraints and the internal structures of membrane channels that make the relevant electrodiffusion properties specific for ion channel problems.
Taking the structural characteristics into consideration, the basic continuum model for ionic flows is the Poisson-Nernst-Planck (PNP) system, which treats the aqueous medium (within which ions are migrating) as a dielectric continuum [9,10,14,16,19,27,28,29,30,31,40,41,42,43,59,60,68,93]:
where X∈Ω with Ω being a three-dimensional cylindrical-like domain representing the channel, Q(X) is the distribution of the permanent charge along the interior wall of the channel, εr(X) is the relative dielectric coefficient, ε0 is the vacuum permittivity; e is the elementary charge, kB is the Boltzmann constant, T is the absolute temperature; Φ is the electric potential, for the ith ion species, Ci is the concentration, zi is the valence (the number of charges per particle), Ji is the flux density, Di(X) is the diffusion coefficient, and μi(X) is the electrochemical potential.
Under some reasonable conditions, the PNP system can be derived as a reduced model from molecular dynamics [95], from Boltzmann equation [3], and from variation principles [56,57,58]. The simplest PNP model is the classic PNP (cPNP) system that contains only the ideal component of electrochemical potential. The cPNP system treats ions essentially as point-charges, and neglects ion size effects. It has been simulated [13,14,16,19,40,48] and analyzed [1,4,5,6,32,39,62,69,72,73,85,97,98,102,104,105] to a great extent. However, a major weak point of the cPNP model is that ions are treated as point of charges, which is only reasonable in the extremely dilute setting. Many extremely important properties of ion channels, such as selectivity, rely on ion sizes critically, in particular, for ions that have the same valence, such as sodium Na+ and potassium K+, the main difference is their ionic sizes. Selectivity of ion channels has been a central issue in the study of cells and tissues at least since Hodgkin, Huxley, and Katz discovered the role of Na+ and K+ currents in the action potential [18,49,50]. Selectivity of ion channels has been theorized to occur is in a variety of ways, ranging from structural discussions [23,24,25,26,79,80,108,109] to scaling models [33], kinetic models [45,46] and electrostatic models [20,21,22]. However, all these different theories of selectivity fail to reproduce experimental measurements over a wide range of conditions.
On the contrary, reduced models, such as the PNP model, using only physical variables, which include the radius of the pore (the channel geometry) and the dielectric constant of the protein, are successful in interpreting the mechanisms that govern selectivity of the L-type Ca++, Na+ channels and also their mutations [9,10,11,12]. It has come as a surprise that a model of selectivity that includes only a few features of the atomic structure has been able to describe the selectivity properties of calcium and sodium channels very well, in all solutions over a wide range of conditions, with only two adjustable parameters using crystal radii of ions. Examining the finite ion size effects on ionic flows, especially for multiple cations with the same valence should provide deep insights into the selectivity phenomenon of ion channels, and this is the motivation of our work.
Ionic flows through ion channels exhibit extremely rich phenomena, which is why ion channels are nano-scale valves for essentially all activities of living organisms. This is the very reason that it is a great challenge to understand the mechanisms of ion channel functions. To study effects on ionic flows from finite ion sizes, one has to consider excess (beyond the ideal) component in the electrochemical potential. One way is to include uncharged hard-sphere potentials to partially account for ion size effects. Physically, this means that each ion is approximated as a hard-sphere with its charges at the center of the sphere. Both local and nonlocal models for hard-sphere potentials were introduced for this purpose [8,91,92]. Nonlocal models give the hard-sphere potentials as functionals of ion concentrations while local models depend pointwise on ion concentrations. The PNP models with ion sizes have been investigated analytically [2,7,61,63,71,76,77,99,106] for two ion species, one positively charged and one negatively charged and computationally [41,42,43,47,56,57,58,68,84,88,96,107] for ion channels and have shown great success. Existence and uniqueness of minimizers and saddle points of the free-energy equilibrium formulation with ionic interaction have also been mathematically analyzed [34,70].
For mathematical analysis, the challenge lies in the fact that specific dynamics depend on complicated nonlinear interplays of multiple physical parameters such as boundary concentrations and potentials, diffusion coefficients, ion sizes and valences, permanent charge distributions, etc. In general, there is no hope to have explicit solution formulae for such a complicated problem even with simple boundary values. The recent development in analyzing classic PNP models [32,72,73] sheds some lights on the voltage-current relationship in simplified settings. This development is based heavily on modern invariant manifold theory of nonlinear dynamical systems, particularly, the geometric theory of singular perturbations. Together with specific structures to PNP models, we are able to, far beyond the existence results, obtain a more or less explicit approximation formula for solutions from which one can further study the qualitative properties of ionic flows and extract concrete information directly related to biological measurements.
In this work, we will study the PNP model with three ion species, two positively charged with the same valence and one negatively charged. Bikerman's local hard-sphere model is included to account for finite ion size effects. Of particular interest is the competition between two cations due to finite ion sizes, which provides useful and deep insights into the selectivity phenomena for open ion channels with given protein structures. Our analysis is based on a further reduction of PNP models. On the basis that ion channels have narrow cross sections relative to their lengths, PNP systems defined on three-dimensional ion channels are further reduced to quasi-one-dimensional models first proposed in [82] and, for a special case, the reduction is rigorously justified in [75]. A quasi-one-dimensional (time-evolution) PNP type model for ion flows of n ion species is
where A(X) is the area of the cross-section of the channel at location X. The boundary conditions are, for i=1,2,⋯,n,
For ion channels, an important characteristic is the I-V relation. Given a solution of the boundary value problem (1.2)–(1.3), the current is
where zkJk is the individual flux of charge of the kth ion species. For fixed boundary concentrations Lk's and Rk's, Jk's depend on V only and formula (1.4) provides a dependence of the current I(V;ε) on the voltage V. In terms of applications, it is important to study properties of individual fluxes Jk due to the fact that most experiments (with some exceptions) can only measure the total current I while individual fluxes contain much more information on channel functions. This is another reason that we mainly focus on the study of individual fluxes in this work. We would like to point out that in general, the I-V relation is not unique for the PNP system with nonzero permanent charge Q(x), even for the classic PNP system with two ion species [32]. However, with the permanent charge Q(x) being zero, the I-V relation is unique, that is, the cPNP system has a unique solution [72]. In our work, we assume the permanent charge to be zero, and view the volume of the ion species as a regular perturbation to the system, and since the linearized system at zero ion-size is nondegenerate, the solution to the PNP system is unique; but the dynamics of the ionic flows is still rich due to the nonlinear interplay between distinct physical parameters.
We comment that our results, for the relatively simple setting and assumptions of our model, are rigorous. We believe these results will provide useful insights for numerical and even experimental studies of ionic flows through membrane channels. At the same time, we point out that the quasi-one-dimensional PNP model and the local hard-sphere model adopted in this paper are rather simple. Aside the fact that they will miss the three-dimensional features of the problem, a major weakness is the omission of the excess electrostatic component in the excess potentials. As a result, important phenomena such as charge inversion and layering may not be detected by this model.
The rest of this paper is organized as follows. In section 2, we set up our problem with further assumptions. In section 3, the existence and (local) uniqueness result for the boundary value problem is established under the framework of the geometric singular perturbation theory. Based on the analysis, treating the ion sizes as small parameters, approximations of individual fluxes are derived, from which the effects on ionic flows from ion sizes are analyzed in details. This leads to our main focus, the competition between two cations due to the nonlinear interplay between finite ion sizes, diffusion coefficients and boundary conditions, studied in section 4. Some concluding remarks are stated in section 5. A detailed proof of Lemma 3.5 is provided in Appendix A.
2.
Problem setup
2.1. Excess potential and a local hard sphere model
The electrochemical potential μi(X) for the ith ion species consists of the ideal component μidi(X) and the excess component μexi(X):
μi(X)=μidi(X)+μexi(X), where
with some characteristic number density C0. The classical PNP system takes into consideration of the ideal component μidi(X) only. This component reflects the collision between ion particles and the water molecules.
It has been accepted that the classic PNP system is a reasonable model in, for example, the dilute case under which the ion particles can be treated as point particles and the ion-to-ion interaction can be more or less ignored.
The excess chemical potential μexi(X) accounts for finite sizes of ions, which is critically important for selectivity−which ion a channel prefers−of ion channel. While channel protein structures play an important role for channel selectivity, the electrodiffusion of ions is clearly another critical component. For different ions with the same valence, their sizes are a crucial factor for the selectivity. The excess potential μexi(X) consists of two components: the (uncharged) hard-sphere component μHSi(X) and the excess electrostatic component μESi. While there are very successful models for μHSi(X), modeling of μESi(X) is itself extremely challenging and is still a very active research area in liquid-state theory of chemistry and physics [34,41,90,91].
In this paper, we will take the following Bikerman's local hard-sphere model to approximate μexi(X)
where νj is the volume of the jth ion species. In particular, in the following analysis, we will take νn=ν so that λn=1.
2.2. The steady-state boundary value problem and assumptions
The main goal of this paper is to examine the qualitative effect of ion sizes via the steady-state boundary value problem of (1.2)–(1.3) with the local hard-sphere model (2.2) for the excess potential. For definiteness, we will take the following settings:
(A1) We consider three ion species (n=3) with z1=z2=−z3=1.
(A2) The permanent charge is set to be zero: Q(X)=0.
(A3) For the electrochemical potential μi, in addition to the ideal component μidi, we also include the local hard-sphere potential μbiki in (2.2).
(A4) The relative dielectric coefficient and the diffusion coefficient are constants, that is, εr(X)=εr and Di(X)=Di.
Remark 2.1. In the study of ion channel problems, the selectivity of cations Na+ and K+ is extremely important. This is exactly the reason that we choose z1=z2=1 together with z3=−1 for the anion Cl−.
In the sequel, we will assume (A1)–(A4). Under the assumptions (A1)–(A4), the steady-state system of (1.2) reads
The boundary conditions become, for i=1,2,3,
We first make a dimensionless rescaling following [39]. Set C0=max{Li,Ri:i=1,2} and let
We would like to point out that the dimensionless parameter ε defined in (2.5) as ε=1l√εrε0kBTe2C0 is directly related to the ratio κD/l, where κD=√εrε0kBT∑j(zje)2Cj is the Debye length; in particular, ε=κD/l when z2j=1 and Cj=C0. Typically, the parameter ε is small due to the fact that the two variables l, the length of the channel, and C0, some characteristic number density could be very large (for many cases, the value of ε is of order O(10−3)).
The boundary value problem (2.3)–(2.4) becomes
with the boundary condition
Remark 2.2. We will take h(x)=1 over the whole interval [0,1] in our analysis. This is because for ion channels with zero permanent charge, it turns out that the variable h(x) contributes through an average, explicitly through the factor 1∫10h−1(x)dx (for example, the individual flux will be DkJk∫10h−1(x)dx, see [71]), which does not affect our analysis of qualitative properties of ionic flows.
Denote
Then, system (2.6) can be rewritten as
Recall that the boundary condition is now
3.
Geometric singular perturbation theory for (2.8)–(2.9)
We will rewrite system (2.8) into a standard form for singularly perturbed systems and convert the boundary value problem (2.8) and (2.9) to a connecting problem.
Denote the derivative with respect to x by overdot and introduce u=ε˙ϕ and τ=x. System (2.8) becomes
System (3.1) will be treated as a dynamical system of phase space R9 with state variables (ϕ,u,C,J,τ).
For ε>0, the rescaling x=εξ of the independent variable x gives rise to the fast system,
where prime denotes the derivative with respect to ξ.
Let BL and BR be the subsets of the phase space R9 defined by
Then the original boundary value problem is equivalent to a connecting problem, namely, finding a solution of (3.1) or (3.2) from BL to BR.
In what follows, instead of studying the boundary value problem, we will consider the equivalent connecting problem for system (3.1) or (3.2) and construct its solution from BL to BR. The construction process involves two main steps: the first step is to construct a singular orbit to the connecting problem, and the second step is to apply geometric singular perturbation theory to show that there is a unique solution near the singular orbit for small ε>0.
Following the idea in [32,71,72,73], we first construct a singular orbit on [0,1] that connects BL to BR. In our coming analysis, we assume the so-called electroneutrality conditions
3.1. Limit fast dynamics and boundary layers
By setting ε=0 in (3.1), we obtain the so-called slow manifold
By setting ε=0 in (3.2), we get the limiting fast system
Note that the slow manifold Z is precisely the set of equilibria of (3.6). It follows from [32,61,63,71,72,73,76] that
Lemma 3.1. For system (3.6), the slow manifold Z is normally hyperbolic.
We would like to point out that the normal hyperbolicity of the slow manifold Z is crucial in our analysis, which guarantees the existence of the stable manifold and the unstable manifold that will be discussed below (see [32,35] for more details for the theory of normally hyperbolic invariant manifolds).
For ν>0 small, treating (3.6) as a regular perturbation of that with ν=0, we look for solutions Γ(ξ;ν)=(ϕ(ξ;ν),u(ξ;ν),c1(ξ;ν),c2(ξ;ν),c3(ξ;ν),J1(ν),J2(ν),J3(ν),τ) of system (3.6) of the form
Lemma 3.2. For ν>0 small, one has, up to the first order in ν,
Proof. A direct computation leads to the result. We omit it here.
Substituting (3.7) into system (3.6), together with (3.8), by careful calculations, we obtain the zeroth order limiting fast system in ν:
and the first order limiting fast system in ν:
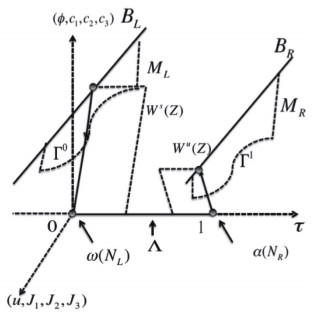
Let ML be the collection of orbits from BL in forward time under the flow of system (3.6) and MR be the collection of orbits from BR in backward time under the flow of system (3.6). Let Ws(Z) be the stable manifold of Z that consists of points approaching Z in forward time, and let Wu(Z) be the unstable manifold of Z that consists of points approaching Z in backward time. Then, for a singular orbit connecting BL to BR, the boundary layer at x=0 must lie in NL=ML∩Ws(Z) and the boundary layer at x=1 must lie in NR=MR∩Wu(Z). Let ω(NL) be the ω-limit set of NL, and α(NR) be the α-limit set of NR, which are defined by
Proposition 3.3. Assume that ν≥0 is small. Under electronutrality conditions (3.4), one has
(ⅰ) The stable manifold Ws(Z) intersects BL transversally at points
and the ω-limit set of NL=ML⋂Ws(Z) is
where Ji(ν)=Ji0+Ji1ν+o(ν),i=1,2,3, can be arbitrary, and
(ⅱ) The unstable manifold Wu(Z) intersects BR transversally at points
and the α-limit set of NR=MR⋂Wu(Z) is
where Ji(ν)=Ji0+Ji1ν+o(ν), i=1,2,3, can be arbitrary, and
Proof. The result for system (3.9), the zeroth order system in ν, has been obtained in [6], we will not repeat it here. For system (3.10), the first order system in ν, it has the following four nontrivial first integrals:
We now establish the results for ϕL1,cL11,cL21,cL31 and ul1 for system (3.10). Those for ϕR1,cR11,cR21 and cR31 can be established in a similar way.
Note that ϕ(0)=c11(0)=c21(0)=c31(0)=0. Using the integrals H1,H2 and H3, one has
Let ξ→∞, careful calculations give
Under electroneutrality conditions (3.4), one has cL10=L1, cL20=L2 and cL30=L3. It follows that cL11=cL21=cL31=0. In view of H4(0)=H4(∞), together with the above analysis, one has ul1=0. This completes the proof.
3.2. Limit slow dynamics and regular layer over [0,1]
We now construct the regular layer Λ on Z that connects ω(NL) and α(NR). Following the ideas in [32,71,72,73], we make a rescaling u=εp and c1+c2−c3=−εq in system (3.1). In term of the new variables, system (3.1) becomes
where c3=c1+c2+εq.
It is again a singular perturbation problem and its limiting slow system is
where c3=c1+c2.
For system (3.12), the slow manifold is
Therefore, the limiting slow system on S is
where c3=c1+c2.
As for the regular layer problem, we look for solutions of (3.13) of the form
to connect ω(NL) and α(NL) given in Proposition 3.3; in particular, for j=0,1,
For convenience, we define quantities Tc0, Tc1, Tm0, Tm1, F1, F2 and a function A(x) as, for k=0,1,
Substituting (3.14) into system (3.13), together with (3.8), by careful calculations, we obtain the zeroth order limiting slow system in ν
and the first order limiting slow system in ν
For the zeroth order system (3.16) (see [6] for details), one has
Lemma 3.4. Under electroneutrality conditions (3.4), there is a unique solution (ϕ0(x),c10(x),c20(x),J10,J20,J30,τ(x)) of (3.16) such that (ϕ0(0),c10(0),c20(0),τ(0))=(ϕL0,cL10,cL20,0,) and (ϕ0(1),c10(1),c20(1),τ(1))=(ϕR0,cR10,cR20,1), where ϕL0,cL10,cL20,ϕR0,cR10, and cR20 are given in Proposition 3.3. It is given by
where
Note that, for x∈(0,1), under (3.4), one has A(x)=1−x+R3L3x>0. For convenience, we define functions Mk(x)=M1(L1,L2,R1,R2;λ1,λ2;x) as, k=1,2,3,4,
For the first order system (3.17), we have (see Appendix A for a detailed proof)
Lemma 3.5. Under electroneutrality conditions (3.4), there is a unique solution (ϕ1(x),c11(x),c21(x),J11,J21,J31,τ(x)) of (3.17) such that (ϕ1(0),c11(0),c21(0),τ(0))=(ϕL1,cL11,cL21,0)=(0,0,0,0), and (ϕ1(1),c11(1),c21(1),τ(1))=(ϕR1,cR11,cR21,1)=(0,0,0,1), where ϕL1, cL11, cL21, ϕR1, cR11 and cR21 are given in Proposition 3.3. It is given by
where J10,J20,J30,Tm0,Tc0 and Mk(x), k=1,2,3,4 are given in (3.15), (3.18), (3.20), and
The next result can be justified directly.
Proposition 3.6. Assume electroneutrality conditions (3.4). Fixing V and treating both the zeroth order approximations Jk0's (in ν) and first order approximations Jk1's (in ν) as functions of boundary concentrations Li and Ri, one has Jk0 is homogeneous of degree one and Jk1 is homogeneous of degree two, that is, for any α>0,
Remark 3.7. This interesting observation actually provides a nice way to adjust the effects on ionic flows (in particular, for the individual flux) from finite ion size by suitably controlling its boundary concentrations. Furthermore, in our later study of the function P(V)=D1J11−D2J21, which provides detailed information that is related to the selectivity of cations due to electrodiffusion properties of ions with a given protein structures, this scaling law can either reduce or enhance the preference of the ion channel for cations.
The slow orbit, up to O(ν),
given in Lemmas 3.4 and 3.5 connects ω(NL) and α(NR). Let ˉML (resp., ˉMR) be the forward (resp., backward) image of ω(NL) (resp., α(NR)) under the slow flow (3.13) on the seven-dimensional slow manifold S. Following the idea in [71,72], we have
Proposition 3.8. There exists ν0>0 small depending on boundary conditions so that, if 0≤ν≤ν0, then, on the seven-dimensional slow manifold S, ˉML and ˉMR intersects transversally along the unique orbit Λ(x;ν) given in (3.21).
3.3. Existence of solutions near the singular orbit
We have constructed a unique singular orbit on [0, 1] that connects BL to BR. It consists of two boundary layer orbits Γ0 from the point
to the point (ϕL,0,cL1,cL2,cL3,J1,J2,J3,0)∈ω(NL)⊂Z and Γ1 from the point (ϕR,0,cR1,cR2,cR3,J1,J2,J3,1)∈z1(NR)⊂Z to the point
and a regular layer Λ on Z that connects the two landing points
of the two boundary layers.
We now establish the existence of a solution of (2.8)–(2.9) near the singular orbit constructed above which is a union of two boundary layers and one regular layer Γ0∪Λ∪Γ1. The proof follows the same line as that in [6,32,71,72,73] and the main tool used is the Exchange Lemma [64,65,66,100] of the geometric singular perturbation theory.
Theorem 3.9. Let Γ0∪Λ∪Γ1 be the singular orbit of the connecting problem system (3.1) associated to BL and BR in system (3.3). Let ν0>0 be as in Proposition 3.8. Then, there exists ε0>0 small (depending on the boundary conditions and ν0) so that, if 0≤ν≤ν0 and 0<ε≤ε0, then the boundary value problem (2.8)–(2.9) has a unique smooth solution near the singular orbit Γ0∪Λ∪Γ1.
Proof. Let ν0 be as in Proposition 3.8. For 0≤ν≤ν0, we define ul=ul0+ul1ν, J1(ν)=J10+J11ν, J2(ν)=J20+J21ν and J3(ν)=J30+J31ν. Fix δ>0 small to be determined. Let
For ε>0, let ML(ε,δ) be the forward trace of BL(δ) under the flow of system (3.1) or equivalently of system (3.2) and let MR(ε) be the backward trace of BR. To prove the existence and uniqueness statement, it suffices to show that ML(ε,δ) intersects MR(ε) transversally in a neighborhood of the singular orbit Γ0∪Λ∪Γ1. The latter will be established by an application of the Exchange Lemma.
Notice that dimBL(δ) = 4. It is clear that the vector field of the fast system (3.2) is not tangent to BL(δ) for ε≥0, and hence, dimML(ε,δ) = 5. We next apply Exchange Lemma to track ML(ε,δ) in the vicinity of Γ0⋃Λ⋃Γ1. First of all, the transversality of the intersection BL(δ)⋂Ws(Z) along Γ0 in Proposition 3.3 implies the transversality of intersection ML(0,δ)⋂Ws(Z). Secondly, we have also established that dimω(NL)=dimNL−1=3 in Proposition 3.3 and that the limiting slow flow is not tangent to ω(NL) in Section 3.2. Under these conditions, the Exchange Lemma [64,65,66,100] states that there exist ρ>0 and ε1>0 so that, if 0<ε≤ε1, then ML(ε,δ) will first follow Γ0 toward ω(NL)⊂Z, then follow the trace of ω(NL) in the vicinity of Λ toward {τ=1}, leave the vicinity of Z, and, upon exit, a portion of ML(ε,δ) is C1O(ε)-close to Wu(ω(NL)×(1−ρ,1+ρ)) in the vicinity of Γ1. Note that dimWu(ω(NL)×(1−ρ,1+ρ))=dimML(ε,δ)=5.
It remains to show that Wu(ω(NL)×(1−ρ,1+ρ)) intersects MR(ε) transversally since ML(ε,δ) is C1O(ε)-close to Wu(ω(NL)×(1−ρ,1+ρ)). Recall that, for ε=0, MR intersects Wu(Z) transversally along NR (Proposition 3.3); in particular, at γ1:=α(Γ1)∈α(NR)⊂Z, we have
where, Tγ1Wu(γ1) is the tangent space of the one-dimensional unstable fiber Wu(γ1) at γ1 and the vector Vs∉Tγ1Wu(Z) (the latter follows from the transversality of the intersection of MR and Wu(Z)). Also,
where the vector Vτ is the tangent vector to the τ-axis as the result of the interval factor (1−ρ,1+ρ). From Proposition 3.8, ω(NL)⋅1 and α(NR) are transversal on Z∩{τ=1}. Therefore, at γ1, the tangent spaces Tγ1MR and Tγ1Wu(ω(NL)×(1−ρ,1+ρ)) contain seven linearly independent vectors: Vs, Vτ, Tγ1Wu(γ1) and the other four from Tγ1(ω(NL)⋅1) and Tγ1α(NR); that is, MR and Wu(ω(NL)×(1−ρ,1+ρ)) intersect transversally. We thus conclude that, there exists 0<ε0≤ε1 such that, if 0<ε≤ε0, then ML(ε,δ) intersects MR(ε) transversally.
For uniqueness, note that the transversality of the intersection ML(ε,δ)∩MR(ε) implies dim(ML(ε,δ)∩MR(ε))=dimML(ε,δ)+dimMR(ε)−9=1. Thus, there exists δ0>0 such that, if 0<δ≤δ0, the intersection ML(ε,δ)∩MR(ε) consists of precisely one solution near the singular orbit Γ0∪Λ∪Γ1.
4.
Competition between cations
In this section, our main interest is the competition between two positively charged ion species due to the nonlinear interplays between finite ion sizes, diffusion coefficients and boundary conditions. Mathematically, this is characterized by the quantity P=D1J11−D2J21 (J11 and J21 are the leading terms corresponding to two cations that include finite size effects), which provides important information of competitions between two cations. For convenience, in the following, we use SI to denote the cation associated with c1 and J1, and SII to denote the one associated with c2 and J2.
Recall from (3.7) that Jk1's (k=1,2) are the main terms that contain ion size effects. From (3.15), Lemmas 3.4 and 3.5, one has
For simplicity in our following discussion, we further assume that λ2>λ1. Define P(V)=P(L1,L2,R1,R2;V;λ1,λ2;D1,D2) as
From Lemma 3.5, P(V) can be rewritten as
with P0(V)=P0(L1,L2,R1,R2;V;λ1,λ2;D1,D2) being defined by
where N1(V)=N1(L1,L2,R1,R2,V;λ1,λ2) and N2(V)=N2(L1,L2,R1,R2,V;λ1,λ2) are defined as follows:
4.1. Competition at singularities
For the function P defined in (4.1), direct calculations lead to the following result, which is crucial for our further study on the qualitative properties of ionic flows.
Lemma 4.1. Assume that V≠0. Under electroneutrality conditions, L3=R3, L3=R3e−V and L3=R3eV are three removable singularities of P(V).
Remark 4.2. From the definition of the function P(V), L3=R3, L3=R3e−V and L3=R3eV are removable singularities of the first order approximations Jk1, k=1,2 in ν of the individual fluxes.
We next consider the competition of two positive charged ion species as L3→R3 and L3→R3e−V, respectively.
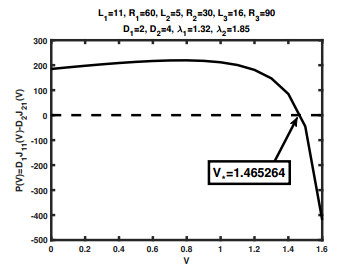
Theorem 4.3. Suppose L1>R1. For small ε>0 and ν>0, there exists a critical potential V∗>ln2 such that, for V>V∗, one has P(V)>0 as L3→R3, that is, the ion channel prefers cation SI over cation SII.
Proof. Direct calculation gives
Under our assumption, one has (λ2−λ1)(L1−R1)Ve−V−1<0, for V>0. Upon introducing K1(V) and K2(V) defined as
Then, as L3→R3, P(V)>0 is equivalent to
Rewrite K1(V) as K1(V)=e−V−12V˜K1(V) with ˜K1(V)=V+2e−V−2. A direct computation gives ˜K1(0)=0 and ˜K1(V)>0 for V>ln2; and ˜K1(V)<0 for V<ln2. Together with e−V−12V<0, one has K1(V)<0 for V>ln2 and K1(V)>0 for V<ln2. Note that K2(V)=K1(V)+VeV−1 with VeV−1>0. Therefore, there must exist a V∗>ln2 such that K2(V)<0 for V>V∗. With L1>R1 and V>0, we have
(ⅰ) R1−L1eV=R1−L1+L1(1−eV)<0, which implies (D1+D2)(R1−L1eV)1−eV>0.
(ⅱ) R2−R1<L2−L1<(L2−L1)eV gives D2V(1−eV)2(R2−R1−(L2−L1)eV)<0.
(ⅲ) (D1+D2)(L1−R1)1−eV<0.
Therefore, with L1>R1, one has, for V>V∗,
This completes the proof.
Theorem 4.4. Suppose D1D2>L2L1 and V>0 (resp. D1D2<L2L1 and V<0). For small ε>0 and ν>0, one has P(V)>0 as L3→R3e−V, that is, the ion channel prefers cation SI over cation SII as L3→R3e−V.
Proof. It follows from P(V)→(D1L1−D2L2)(eV−1)2(λ1L1+λ2L2+R3e−V)V as L3→R3e−V.
4.2. Competitions away from singularities
For fixed boundary concentration R3 and boundary electric potential V>0, the removable singularities L3=R3, L3=R3eV and L3=R3e−V split the L3-region into four subregions: (0,R3e−V), (R3e−V,R3), (R3,R3eV) and (R3eV,+∞), over which the sign of P can be analyzed. Our study will mainly focus on the sign of P over the first subregion (0,R3e−V).
To get started, we establish some results which are crucial to study the sign of P(V), and will be frequently used in our following analysis. Note that, under electroneutrality conditions (3.4), from (3.18), one has
and from (3.15), (5.3) and (5.4), together with A(1)=R3/L3, we have
where
It then follows that
Lemma 4.5. Under electroneutrality conditions, one has
(ⅰ) For L3<R3e−V, one has F1<0 (resp. F1>0) if L1L2<R1R2 (resp. L1L2>R1R2).
(ⅱ) For L3>R3e−V, one has F1<0 (resp. F1>0) if L1L2>R1R2 (resp. L1L2<R1R2).
Lemma 4.6. Fixing V>0. Then,
(Ⅰ) For R3<1, one has
(ⅰ) q1(V;L3,R3)>0 if L3<R3;
(ⅱ) There exists an L∗3>R3 such that q1(V;L3,R3)<0 if R3<L3<L∗3 and q1(V;L3,R3)>0 if L3>L∗3.
(Ⅱ) For R3>1, one has q1(V;L3,R3)>0 if L3<R3; q1(V;L3,R3)<0 if L3>R3.
Lemma 4.7. q2(L3,R3)>0 if L3>R3; and q2(L3,R3)<0 if L3<R3.
Based on Lemma 4.6, we further assume R3>1 in the following argument (the case with R3<1 can be discussed similarly). From the electroneaurality conditions (3.4), one has the following possibilities for L3<R3e−V:(a) L1<R1e−V and L2<R2e−V; (b) L1<R1e−V and L2>R2e−V; and (c) L1>R1e−V and L2<R2e−V. In this section, we will only consider the case (a), which, with V>0, is equivalent to
and study the sign of P, which provides rich dynamical behavior of ionic flows. The other two cases can be analyzed in a similar way, and we leave them to interested readers. From Lemmas 4.5–4.7, we obtain
Lemma 4.8. Under assumption (4.6), one has J10<0, J20<0, J30<0, Tm0<0 and Tc0>0. Furthermore, if L1L2>R1R2, then Tm1<0 and Tc1<0.
Our main result now follows.
Theorem 4.9. Assume (4.6), L1L2>R1R2 and R1−L1R2−L2<D2D1. Then, for small ε>0 and ν>0, there exists a critical potential V∗>0 such that for 0<V<V∗, one has P(V)>0, that is, the ion channel prefers cation SI over cation SII.
Proof. Note that, under our assumption, PP0>0. Instead of showing that P>0, we will prove that P0>0. Recall from (4.2),
where N1 and N2 as defined in (4.3). From Lemma 4.8, one can easily check that for the second term in P0, one has −(D1J10+D2J20)(λ2−λ1)F1Tc0L3Tm0(A(1)−1)>0. Next we show that, under our assumption, (D2J20−D1J10)N1+(D1+D2)(J10+J20)N2>0 for 0<V<V∗, where V∗ is identified at the end of our proof. For convenience, we rewrite N1 and N2 as
where
Notice that, with L1<R1e−V and L2<R2e−V,
Together with Lemma 4.8, one has N10>0 and N20>0.
Finally we prove that
From (3.15), (3.18) and (5.3),
which is true under our assumption. It suffices to show that
which is, from Lemma 3.4 and Lemma 4.8, equivalent to ω(V)<0, where ω(V):=ω(V;L1,L2,L3,R1,R2,R3;D1,D2) is defined as
With R1−L1R2−L2<D2D1, a careful calculation leads to ω(0)=0; ω′(0)<0 and ω″(V)>0 for V>0. It follows that the curve ω(V) is concave up for V>0 with its minimum being negative. Therefore, there exists a unique Vg such that ω(V)<0 for 0<V<Vg. Define V∗=min{Vg,lnR1L1,lnR2L2}, one has P(V)>0 for 0<V<V∗.
Remark 4.10. In Theorem 4.9 (see also Theorems 4.3 and 4.4 in Subsection 4.1), under electroneutrality boundary concentration conditions, we study the competition between two cations in terms of the function P defined in (4.1), which provides useful insights for the study of ionic flows through membrane channels, in particular, the selectivity of cations due to the electrodiffusion property of ions with given protein structures of ion channels (another important factor in studying ion selectivity). Distinct effects of the nonlinear interplays between the physical parameters, such as relative ion size (λ1,λ2), diffusion coefficients (D1,D2), boundary concentrations (L1,L2,L3), (R1,R2,R3) and boundary potential V are characterized in a great detail. For example, under the assumption of (4.6), L1L2<R1R2, and R1−L1R2−L2<D2D1, one is able to identify some critical potential V∗, such that for 0<V<V∗, the ion channel prefers cation SI over cation SII. Together with the scaling law stated in Proposition 3.6 and further illustrated in Remark 3.7, the preference of ion channels for distinct cations could be either reduced or enhanced by choosing some suitable positive parameter α in Proposition 3.6.
To end this section, we perform numerical simulations for the system (3.1) directly with small ε and ν to detect two critical potentials identified in Theorem 4.3 and Theorem 4.9, respectively (Figures 2 and 3).
5.
Concluding remarks
We studied a quasi-one-dimensional PNP model with three ion species, two positively charged with the same valence and one negatively charged, and Bikerman's local hard-sphere potential accounted for ion size effects on ionic flows. Under the framework of a geometric singular perturbation theory, the existence and uniqueness of the boundary value problem was established. Furthermore, treating the ion sizes as small parameters, both zeroth order and first order approximations (in ν) to individual fluxes are derived. Of particular interest is to examine the competition between two positively charged ion species for open ion channels with given protein structures, which provides useful insights into the study of selectivity phenomena. Based on our rigorous analysis, we are able to characterize the distinct effects of the nonlinear interplay between physical parameters, such as relative ion size (λ1,λ2), diffusion coefficients (D1,D2), boundary concentrations (L1,L2,L3), (R1,R2,R3) and boundary potential V, which provides an efficient way to control ionic flows. These are the novelty and main contribution of our work. The results, although established for simple biology settings have demonstrated extremely rich dynamics of ionic flows and sensitive dependence on all those physical parameters. More complex phenomena for more realistic ion channel models are expected. We would like to point out that the topic studied in this work is closely related to artificial nanopores as well, where modeling mainly focuses on computing device functions: ionic currents as responses to the voltage as a stimulus (see [36,38,78,89,101] for more details). We believe this work will be useful for future numerical studies, stimulate further analytical studies of ionic flows concerning the selectivity of cations, and even provide useful insights into biological experiments.
Appendix A. We provide detailed proof for Lemma 3.5 in section 3.2.
Proof of Lemma 3.5 From c11 and c21 equations in (3.17), one has
Together with Proposition 3.3, one has
From (3.18), together with x=2L3Tm0(1−A(x)), we have
Therefore,
Evaluating Eq (5.2) at x=1, we have
It follows that
Solving the ϕ1 equations in (3.17), we have
Note that, from (3.18) and (5.2), together with 1−A(x)=Tm02L3x, one has
Therefore,
Evaluating ϕ1(x) at x=1 gives
By the variation of constant formula, one has, with cL11=cL21=0,
where, from (3.18), (5.1) and (5.2),
Evaluating ϕ1(x), c11(x) and c_{21}(x) at x = 1, the expressions for J_{11}, J_{21} and J_{31} follows directly.
Acknowledgments
The authors are grateful to the anonymous referees whose suggestions have in our opinion, significantly improved the paper. J. Chen and M. Zhang were partially supported by MPS Simons Foundation (No. 628308).
Conflict of interest
The author declares no conflicts of interest in this paper.









 DownLoad:
DownLoad: