Deflection is a crucial indicator to reflect the operating condition of girder bridges, which can be used to evaluate structure condition and identify abnormal loading. The paper analyzed the deflection characteristics of long-span girder bridges based on the coupling vibration between stochastic traffic stream and bridge. First, the latest research advances were integrated to form an analytical model of the coupling vibration between stochastic traffic stream and bridge. Then, a generalized Pareto distribution model based on peaks-over-threshold theory was established to predict the extreme girder deflection. Next, a cellular automaton based microsimulation method was proposed to model the traffic loads on bridges, which utilized the intelligent driver car-following model and acceptance distance based lane-changing model. Finally, these theories were applied in the case study of a long-span prestressed concrete continuous girder bridge. It is discovered from the study that, under the coupling vibration between stochastic traffic stream and bridge, the predicted extreme deflection of the case bridge is far lower than the specified design value. Hence, a grading warning model was established and employed to the analysis of deflection monitoring data of the bridge, showing a wide potential prospect of application.
1.
Introduction
The long-span girder bridge, which has the advantages of simple structural configuration, mature construction technology, and low maintenance cost, is a very competitive structural type within the span length of 50–300 m. However, most of these bridges are suffering the long-term down-warping issue with the increase of service life, which largely influences the normal use and safety of these bridges. For example, the Koror-Babeldaob Bridge built in 1977 reached a maximum deflection of 1.2 m in 1990, and still collapsed though being strengthened [1]. Similar cases of long-term down-warping trouble of long-span girder bridges could be found in other countries [2,3]. To solve this issue, it is not only required to understand its original causes from the perspective of design, construction and operation, and update the service life models of the bridge [4], but also to conduct long-term monitoring of girder deflection. In doing so, the operating state and the management and maintenance of the bridge could be well understood, which effectively raise the usability of the bridge and prevent hidden safety hazards [3,4].
The health condition of a bridge can be reflected by many structural parameters, such as frequency, strain, and deflection. Among them, deflection is a crucial parameter which represents the overall bridge health condition [5]. In order to identify the bridge condition, it is very important to carry out real-time dynamic monitoring on girder deflection. Many studies identify bridge state and evaluate damage through the collected structural deflection information. Its core mechanism is that if the structural deflection exceeds the expected value under a given loading scenario, the structure is damaged compared to its designed state, and the over-limit level reflects the extent of structural damage. Cao et al. [6] compared the use of fundamental mode shape and static deflection for structure damage identification; Zhang et al. [7] used deflection shape curvature extracted from the dynamic response of a passing vehicle to detect structure damage; Elhattab et al. [8] used bridge displacement profile difference to localize damage. These damage analytical methods could complete the numerical verification and laboratory model verification. However, they are not such practical to the monitoring data of realistic bridges. This is mainly because the environmental excitation source of a real bridge is complex, with large environmental noise interference. However, it is feasible to analyze whether the deflection change of the realistic bridge is within a predicted range on the basis of the above ideas. Exceeding the predicted value indicates structural damage, and the management and maintenance strategies should be adjusted, for example, mitigating traffic load, or intensifying routine maintenance frequency.
For long-span girder bridges, vehicle, temperature and long-term down-warping are the main factors causing structural deformation. In which: long-term down-warping can be obtained by long-term tracking test, but this factor is a result under the complex action of structure and environment [2,3]; temperature load, due to its periodicity and limited range, shows limited influence to the structure, so it is not the main cause of structural damage; vehicle load is the main factor leading to instant structural deformation, and overload and heavy load are easy to damage the structure, so the accumulation of damage may be an important fuse for long-term down-warping or even sudden structural failure[9,10]. Therefore, the warning and analysis of deflection should be established based on the fine analysis of girder deflection induced by traffic-bridge interaction.
For the deflection change of long-span girder bridge under the action of vehicle load, it is necessary to make an analysis of the coupled vibration between stochastic vehicle stream and bridge on basis of the vehicle load information investigated in the bridge site, master the time history of bridge deflection within a certain period, and build an extreme deflection model according to the deflection time history information, so as to forecast the possible extreme deflection of the bridge structure in a long period of time. Recently, in the study of bridge traffic load, the Monte Carlo method was widely used to generate stochastic vehicle sequences [11]. However, as for long-span bridges, the acceleration, deceleration, and lane changing behaviors of individual vehicles in the process of driving over the bridge span should be taken into consideration, so it is required to use microcosmic traffic stream simulation technology, which is relatively a new research area [12,13,14]. Some scholars tried to precisely modeling the action of the stochastic traffic stream, and made a refinement consideration of the axle load information of individual vehicles and the load spacing between vehicles [12,13,14]. As they mainly focused on the bridge safety problem in extreme congestion condition, so they didn't take into consideration of the coupled vibration of vehicle and bridge. The other scholars thought about using the vehicle bridge coupled vibration to evaluate the structural safety and fatigue under the action of vehicle and wind load [15], but their microscopic simulation method of the stochastic traffic stream is not accurate enough [12]. Therefore, only forming a refined microscopic traffic stream simulation method and considering the coupled vibration of stochastic traffic stream and bridge can accurately analyze the deflection characteristics of bridge structure under operating traffic.
Based on the basic mathematical theory of vehicle-bridge coupling vibration, this paper built an analytical method of the coupled vibration between stochastic traffic stream and bridge, and analyzed the time history response of bridge structure under the operating traffic condition. Then, according to the classical extreme value theory, a method to predict the extreme girder deflection based on short-time simulation data was built, which can obtain the deflection characteristic under any evaluation periods and provide the foundation for bridge state warning. Next, a cellular automaton based microscopic traffic stream load modeling approach was built, which can simulate the stochastic traffic stream load evolution under given traffic conditions. Finally, combined with a long-span prestressed concrete continuous girder bridge, the paper analyzed the deflection characteristics of this bridge in the process of operation using the proposed mathematical method, and proposed a grading warning system on girder deflections of the bridge, which could be used in bridge operating condition assessment based on deflection monitoring data.
2.
Coupled vibration model of stochastic traffic stream and bridge
2.1. Vehicle dynamic model
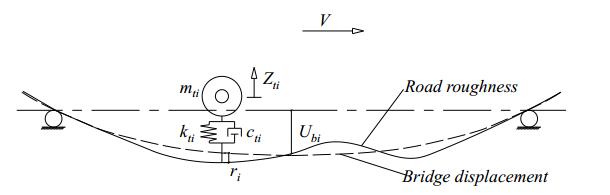
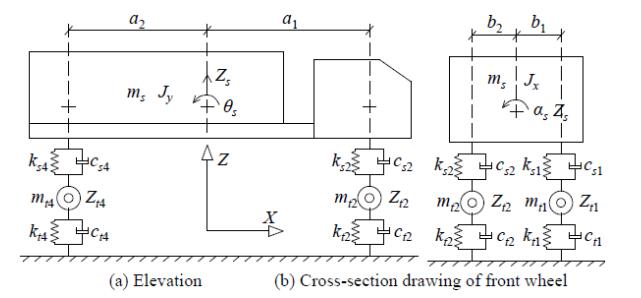
There are various vehicle dynamic models, in which the quality spring model, half-vehicle model, and full vehicle model are frequently used. In the structural dynamic analysis, quality spring model simplifies the vehicle to a larger extent, which will cause large computational deviation; the full vehicle model can fully consider the vertical and horizontal swing characteristics of a vehicle, with high computational accuracy. In the paper, the full vehicle model is utilized. Figure 1 describes the full model of a two-axle vehicle which has seven freedom of motion. The car body is a rigid body supported on a suspension system, with three freedom of motion: vertical translation (Zs), horizontal swing (αs) and vertical swing (θs). Each suspension system is independent and is composed of a damper (csi) and linear spring (ksi). The generalized mass of car body is defined by its mass distribution and physical dimension, all the weight (mti, I = 1, 2, 3, 4) of vehicle wheel, action bar and axle concentrate on the mass block of vehicle wheel, and a damper(cti) and a linear spring (kti) are used to simulate vehicle wheel respectively. The values of relevant parameters of the vehicle model with different axial types can be obtained by referring to the literature [16,17].
Taking a two-axle full vehicle model as an example, the vehicle vibration equation can be established as below:
Where: M, K, and C are the mass stiffness matrix, spring stiffness matrix, and damping stiffness matrix, respectively; z″, z′, andzare the acceleration, speed, and displacement of vehicle motion; Fb-v is the force of the bridge on a vehicle, mainly reflected by the contact force between vehicle tires and bridge pavement.
2.2. Road roughness
The realistic bridge pavement is rugged, which obviously affect the vibration characteristic of a vehicle and influence the coupling vibration behavior of the vehicle bridge system. The road roughness characteristics are usually assumed to be smooth and Gaussian random process. There are many assumptions about road roughness, and the frequently-used is the ISO/WG4 standard. The trigonometric series method is adopted to simulate the road roughness, where the road roughness signals are decomposed into a series of sine waves or other harmonic waves with different frequencies and amplitudes. The road roughness samples are the cumulative sum of these harmonic waves, as below:
Where: N is a sufficiently large number to ensure the integrity of trigonometric series decomposition; φk is random number evenly distributed within the range of 0–2π; x is the vertical coordinate value of bridge pavement; Gd(nk) is the time-frequency spectral density function, which can be converted into the space-frequency power spectral density function according to the vehicle velocity v, i.e. Gd(n)v = Gd(Ω); nk is the kth discrete spectrum value, nk = n1 + (k–0.5) [(n2–n1)/L].
The normal vehicle velocity is between 36 km/h–180 km/h, so it is calculated that the main space frequency as n = 0.01–5.00 cycle/s, saying n1 = 0.01, n2 = 5.00, which is the target spectral range required to consider in the analysis. G(n) can be figured out according to road grade through the following equation:
Where, Ω is the space-frequency, with the unit as cycle/m; Ω0 is 1/2π = 0.16cycle/m; W1 and W2 are valued according to the road grades: A(excellent), B(good), C(general), D(bad) and E(very bad).
2.3. Vehicle bridge coupling vibration equation
The purpose of vehicle-bridge coupling vibration analysis is to solve the vehicle motion equation and bridge motion equation. The vehicle motion equation is shown in Eq. (1), and the bridge motion equation is:
Where: M, K, and C represent the mass stiffness matrix, spring stiffness matrix, and damping stiffness matrix; u″, u′, and u are the acceleration, velocity, and displacement of the bridge motion; the subscript b refers to the bridge subsystem; Fv-b is the force of bridge on the vehicle.
Due to the complex of bridges, it is usually required to divide many units to clearly calculate the structural vibration, so it is very difficult to solve these equations. In most cases, the modal composite superposition method is used to calculate, thus significantly improving the computational analytical efficiency. According to the superposition principle of modal shape, the modal dynamic equilibrium equation of the bridge can be obtained:
Where A is the normal coordinates of the bridge, ϕ is the vibration mode matrix of the bridge.
Thereby, the finite element software can be used to work out the mass matrix, stiffness matrix, damping matrix, and modal matrix of the bridge, and the displacement time-histories of the bridge structure can be solved, Where, the key is to determine the force of vehicle on the bridge (Fv-b). For any vehicle wheel, the vehicle bridge contact can be displayed in Figure 2, then the contact force Fti between vehicle wheel and bridge can be calculated as below:
Where: kti is the vertical stiffness of the ith vehicle wheel, cti is the vertical damping of the ith vehicle wheel, and △i is the displacement difference between vehicle wheel of the ith vehicle wheel and bridge pavement.
Evidently, the displacement difference between the vehicle wheel and bridge pavement can be calculated through the following equation:
Where: Zti is the displacement of the contact position between the ith vehicle wheel and bridge pavement; ui(x, t) and vi(x, t) are the bridge displacement and corner of contact position between vehicle wheel and bridge pavement respectively; ri(x) is the road roughness function at the ith vehicle wheel.
According to the above analysis, the coupling between the vehicle system and the bridge system is established. For the ith vehicle wheel, Fvi-b = FGi–Fti, in which, FGi
= –(msi +
mti)g, msi is the vehicle body weight distributed to this vehicle wheel, and mti is the weight of this vehicle wheel. Therefore, iterative computations are used to solve Eqs 1 and 4 at any moment, and obtain the bridge-vehicle displacement, velocity and acceleration time-history.
2.4. Stochastic traffic stream and bridge coupling vibration model
The coupling vibration equation of a single vehicle and bridge can be simply built and solved. However, if taking into consideration the actions of multiple vehicles on the bridge, the vibration equation become complex. Here, the equivalent wheel load method used in the vehicle-bridge coupling vibration analysis under the action of stochastic traffic stream proposed in the literature [15] is referred for analysis. Through verification, this method can satisfy the computational accuracy need. Under the equivalent vehicle load method, the equivalent force of a vehicle is:
Where: F(t) refers to the equivalent wheel load at moment t, nv is the total vehicle quantity on the bridge at moment t; n is the modal series used in the vehicle-bridge coupling analysis; Gj is the weight of the jth vehicle; xj(t) is the longitudinal location of the jth vehicle on the bridge at the moment t; dj(t) is the transverse location position of the jth vehicle on the bridge at the moment t; hkand αk are the vertical and torsional mode in the kth bridge mode; Rj is the load coefficient of dynamic wheel, i.e. Rj(t) = DWLj(t)/Gj. DWLj(t) is the dynamic wheel load of the bridge at moment t, which is calculated as below:
Where: L and R represent the left wheel and the right wheel, na is the number of axles of the jth vehicle; K and C are the spring stiffness and damping of the wheel; Y and Y' are the relative displacement and velocity of mass block.
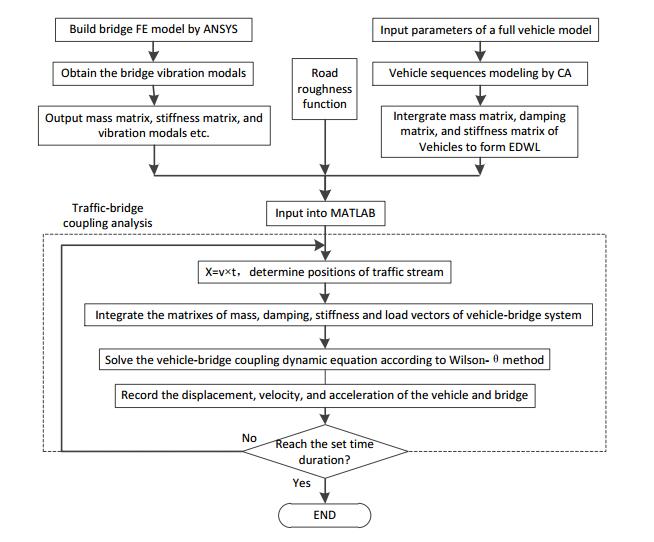
Based on above equivalent wheel load method (for further information, the readers are referred to [15]), the vehicle-bridge coupling vibration issue under the action of stochastic traffic stream could be easily figured out, and the Wilson-θ method can be employed to solve the separation of vehicle vibration equation and bridge vibration equation. The analytical process is summarized in Figure 3.
3.
Extreme value modeling of traffic load effect
Traffic load is integrated with high randomness both in time and space. In the design or evaluation of bridges subjected to traffic load, characteristic load effects in a long period (such as 1000 years) are generally used. However, it is only possible to obtain bridge traffic load effects in short periods due to the limited service life of measuring sensors. Therefore, extreme value modeling theory is needed.
In the research field of bridge traffic load, many scholars studied extreme extrapolation methods. The generalized extreme value distribution model based on block maxima is frequently used. In the block maxima theory, only the maximum from each block is selected, which does not take full use of the extreme information of initial data. When the initial data are limited, the presumption effect of this method will be poor. While, the peak-over-threshold theory uses peak values that exceed a certain threshold in each block, which uses more information of initial data, and has been proved to perform better than the block maxima theory in many fields. This paper adopts the peak-over-threshold theory to predict the extreme traffic load effect.
Suppose the sequence of bridge traffic load effects is Xi(I = 1, 2, …, n), its distribution function is F(x). When setting an upper extreme point, u, If Xi > u, then Xi–u is denoted as the excess, and its distribution function is:
In the Extreme Value Theory, maxima picked from blocks follow the independently identically distribution, and its distribution function could be well represented by the generalized extreme value distribution family. Similarly, as for peaks over threshold samples, when the threshold value is large enough, it is possible to use the generalized Pareto distribution (GPD) as its limit distribution function:
Where, ξ, σ, and u are the shape, scale, and location parameters of the GPD, respectively.
GPD distribution type is completely determined by ξ. ξ = 0 is exponential distribution, ξ > 0 and ξ < 0 shows trailing and censored characteristics respectively. The key to the GPD model is to estimate the shape, scale, and location parameters. Generally, it needs to estimate the location parameter (threshold) first, and then determine the shape and scale parameters. Herein, the goodness test approach is used to estimate these parameters. For a given sample X(I = 1, 2, …n), X(1) < X(2) < … < X(n), the estimation procedures are detailed as follows: first, determine the threshold value u = X(i), and use the maximum likelihood method to estimate the other parameters ξ and σ; then, substitute these parameters into the distribution function of GPD, zj = 1 – [1 + ξ(Xj–u)/σ]–1/ξ, and figure out the distribution of the peaks-over-threshold samples, zj(j = i, …, n); next, conduct the k-s test on the empirical cumulative distribution of zj and the fitting distribution; finally, check the fitting error, if it meets the 5% confidence level then these parameters are the optimal, otherwise re-select the threshold I = I + 1 and repeat above processes.
4.
Cellular automaton based microscopic traffic stream simulation
4.1. Cellular automaton based traffic modeling system
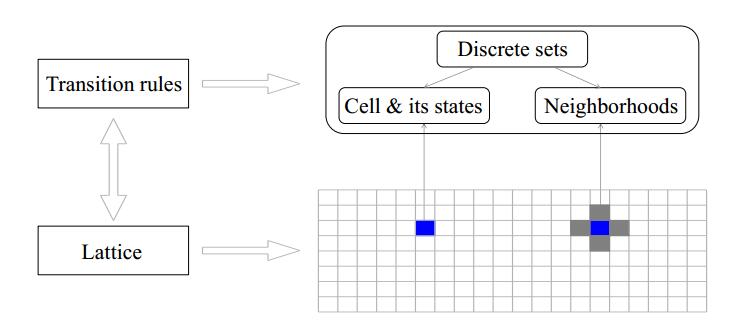
A Cellular automaton is a dynamic system built in discrete time and space, which is widely applied in biological, electronic, mechanical, construction and relative fields [18]. Its basic principle is presented in Figure 4. Any simulated object can be dispersed into cells with a certain shape, forming the lattice. A lattice includes the cells and their states. Any cell and its state define the basic attribute of this cell. The neighborhoods define how the surrounding environment could influence the state of this cell. Transition rules are interactions between cells. Therefore, a typical cellular automaton includes four components of lattice, cells' states, neighborhoods, and transition rules.
For traffic stream simulation, the road can be regarded as the lattice that is divided both longitudinally and laterally. The longitudinal division mainly considers that a vehicle occupies only one cell at any time, and the lateral division is conducted based on the number of traffic lanes. The dimension of the lattice is rectangular, so the traffic stream system is a two-dimensional grid space. The mathematical set of the lattice can be expressed by the following equation:
Where: l refers to the length of road in traffic stream simulation; n is the number of traffic lanes; s is the cell shape; r is the road information, such as lane closure, weight limit, car-following distance control, etc.; △l is the cell size, usually being the average vehicle length of 5–8 m; △t is the simulated time step, set as 1s.
When the lattice is defined, it needs to determine the cell state, including load parameters, dynamic parameters, and motion parameters of vehicles, as shown in the following equation. f represents whether the cell is occupied by a vehicle or not. A vehicle cell indicates that the cell is occupied by a vehicle, i.e., f = 1; a non-vehicle cell indicates that there is no vehicle in the cell, i.e., f = 0. M represents the vehicle load information of a vehicle cell, including weight, axle weight, and axle spacing, etc., which are used to determine the vehicle load distribution on the road. F represents the dynamic parameters of a vehicle cell, which is required for vehicle-bridge coupling analysis. W represents the motion parameter of a vehicle cell, which is composed of velocity, maximum velocity, and vehicle distance, etc.
Once the cell state is defined, it needs to confirm the neighborhoods of a certain vehicle, i.e. the surrounding vehicles that may influence its driving behaviors. For a single-lane traffic cellular automaton, the vehicle at the front of the target vehicle is its neighborhoods, since the front vehicle determines its car-following features. For a multi-lane traffic cellular automaton, the front vehicle of the target vehicle in the same lane, and the front and rear vehicles at the adjacent lanes are its neighborhoods, which determine the car-following and lane-changing features of the target vehicle.
The last is the transition rule of cells, i.e. the traffic rules, which make the cells in the neighborhoods interact with each other and progress the evolution of the system. For the traffic system, two traffic rules of car-following and lane-changing are considered as below.
4.2. Intelligent driver car-following model
The intelligent driver model uses few parameters to describe the car-following behaviors of vehicle, as shown in the following equation. The model is verified that it could well fit many observed traffic phenomena and reproduce various traffic forms from free stream to congestion [12,19].
Where: v0 is the ideal driving velocity; s0 is the static safety distance; T is the safety time interval; Sn* is the driver's expected distance under the current state; vn(t)T represents that the driver attempts to maintain a constant time headway; a is the starting acceleration; b is the comfortable deceleration; δ is the acceleration index, generally δ = 2.
It can be seen that the intelligent driver model determines the vehicle following behavior according to the acceptable acceleration criteria. If the current following distance allows the acceleration operation, the vehicle will accelerate. When a collision risk exists, the vehicle will decelerate. Otherwise, the vehicle moves forward at a constant speed. The intelligent driver model shows clear physical meaning, and is easy for implementation. In the model, the safety time interval, starting acceleration and comfortable deceleration are calibrated by many studies, and the parameter values are shown in Table 1.
4.3. Acceptable distance lane-changing model
Individual vehicles always choose the traffic lane that is comfortable for driving. The vehicle lane-changing behavior defined in the cellular automaton is built on acceptable distance, and the rules are defined as below.
First, the target vehicle cannot accelerate at the current traffic lane:
Then, if the target vehicle changes to the adjacent lane, it can accelerate:
Meanwhile, it will not collide with the rear vehicle if it changes to the adjacent lane:
Where: vit is the velocity of the target vehicle; gapit is the following distance between the target vehicle and its front vehicle; gapi, ft is the following distance between the target vehicle and its front vehicle at the adjacent lane; gapi, bt is the following distance between the target vehicle and its rear vehicle at the adjacent lane.
Based on the above conditions, the target vehicle will change to the target lane with a certain probability. Hence, the traffic system will evolution based on the defined lattice, cells' states, neighborhoods, and traffic rules in the cellular automaton.
4.4. Microscopic traffic stream simulation procedures
With the defined cellular automaton approach, the random traffic stream on long-span bridges can be simulated in a microscopic perspective. Its basic simulation process is summarized as follows:
(1) Obtain the mathematical statistical models of vehicle arrival and vehicle information (such as weight, axle weight, and axle spacing, etc.) based on measured traffic load data;
(2) Generate vehicle at the given time t, according to the time headway statistical model and the average hourly traffic volume change rule;
(3) Determine the vehicle type according to the composition proportion of different vehicle types if a vehicle is generated at the current moment;
(4) Determine which lane the current vehicle will occupy according to the lane-choice probability of different vehicles;
(5) Generate velocity, weight, axle weight and axle distance based on their statistical models of different vehicle types for the current vehicle;
(6) Choose the dynamic parameters based on the type of the current vehicle for vehicle-bridge interaction analysis;
(7) Disperse the simulation road into a lattice, and store these vehicle parameters into the cells' states.
(8) Put the generated vehicle at the starting position of the road, and perform the car-following model and lane-changing model on each vehicle to make vehicles travel on the road;
(9) Repeat these steps until the simulation time is over. The stochastic traffic stream loading condition on the long-span bridge can be generated, and the stochastic traffic load effect of any given traffic condition and traffic parameter can be simulated based on the traffic bridge coupling analysis in Section 2.
5.
Example application
5.1. Bridge overview
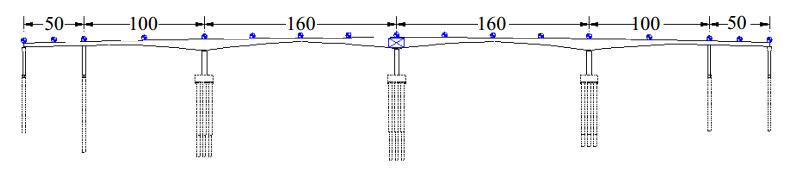
A long-span prestressed concrete continuous girder bridge is illustrated. The arrangement of the bridge is 50 + 100 + 160 + 160 + 100 + 50 m, carrying two-lane unidirectional traffic. The girder uses varied box sections. The bridge was open to traffic in 1996, and has been served for more than 30 years. Recent structure detection on the bridge indicates there are water seepage and crystallization problems. In order to understand the technical state of the bridge, a health monitoring system is established to real-time monitor the bridge deflection, as shown in Figure 5. The road roughness of the bridge pavement is regarded as "general" (C) based on field observation.
5.2. Collection and statistics of traffic loads
Weigh-in-motion (WIM) system has been installed in the highway since 2016. 4-month traffic load data of the bridge site were used for the investigation and analysis of traffic load. Table 3 shows the statistics of truck loads. It is noted light vehicles (such as car and bus etc.) have negligible effects on bridge loading, and therefore are not considered in the traffic bridge coupling analysis. It is found that the average truck weight in the slow lane is obviously higher than that in the fast lane. The overall truck traffic volume is 6646 vehicles per day, which is high for a two-lane highway.
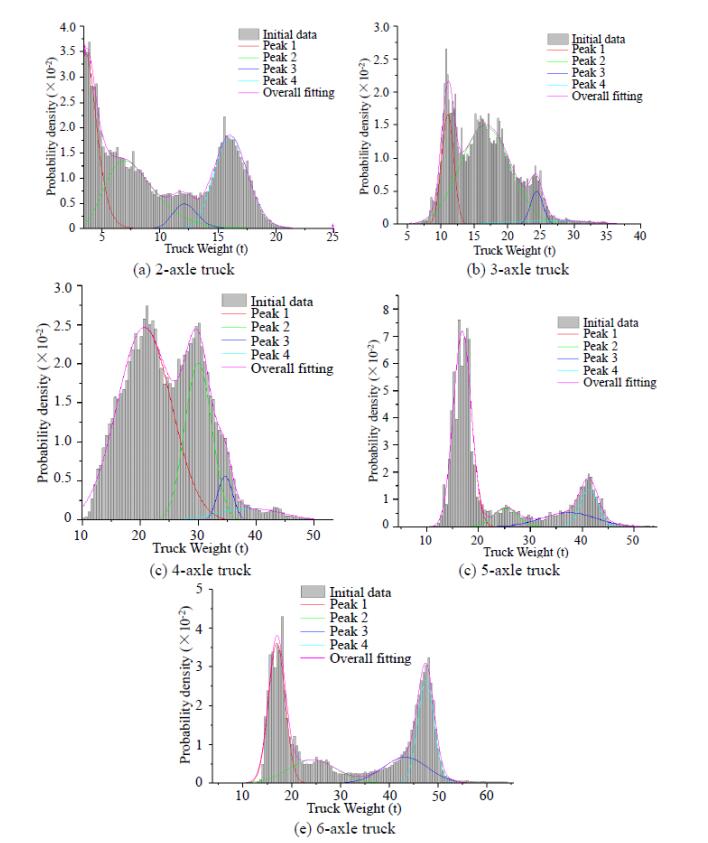
The characteristics of truck weights are very important for the bridge loading effects. A refine modeling of truck weights is performed as shown in Figure 6. It is shown that the use of multi-peak distribution models could well describe the distribution of truck weights, indicating that the vehicle weight can be randomly simulated on the basis of multi-peak distribution models. Moreover, it can be seen that the truck weights are basically lower than 55 t (the weight limit defined in the Chinese bridge design specification). Only few trucks that have many axles exceed the specified weight limit, suggesting that the realistic vehicle stream is basically within the specified load range.
Table 3 gives the fit parameters of multi-peak distributions on different axle-type truck weights. Among them, the two-axle truck has a left truncation, and could be well fit by the lognormal distribution, and therefore the multi-peak lognormal distribution is employed. Other axle-type trucks can obtain a good fitting by using multi-peak normal distribution. Based on these established truck weight distribution model, a stochastic traffic stream simulation can be carried out by generating the vehicle weight from these given distributions.
5.3. Time-history of girder deflection
Combined with the proposed cellular automaton based stochastic traffic stream simulation method and vehicle bridge coupling vibration method, a dynamic girder deflection analysis under stochastic traffic loading was carried out, and the deflections of the mid-span, secondary mid-span, and side-span of the bridge were considered.
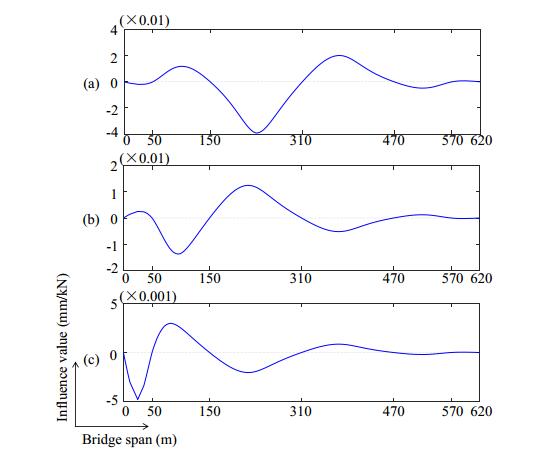
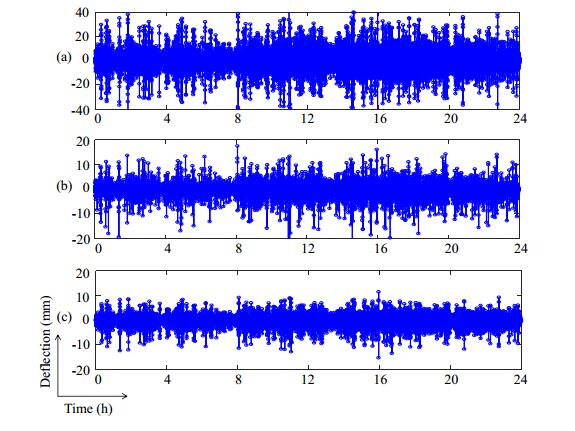
Figure 7 shows the influence line distribution of the girder deflection. It can be seen that the mid-span deflection demonstrates the most obvious structural change, with the maximum influence value reaching to 0.04 mm/kN. Moreover, the structural state change will be reflected in the girder deflection influence line. Based on the three deflection influence lines, the dynamic traffic load effects under the stochastic traffic stream are calculated. In the analysis, the first ten series of modals of the bridge are selected to work out the dynamic effect using modal synthesis method. Finally, the bridge time-history deflections under the stochastic traffic stream are shown. Figure 8 shows the time-history girder deflections with "general" grade of road roughness over a day. The mid-span deflection changes between –40–40 mm, and the secondary mid-span deflection changes between –20–20 mm.
Road roughness has a considerable effect on girder deflections of bridges subjected to traffic loading. Considering potential maintenance or degradation of the pavement of the studied bridge, another two grades of pavement condition (road roughness) being "good" (B) and "bad" (D) are compared. The statistical results of girder deflections caused by the three degrades of road roughness are shown in Table 4. The results indicate that the mean, the 95% quantile, and the maximum values of girder deflections increase when the road roughness grade changes from "good" to "bad". The increased rates of girder deflections under "good" and "bad" condition are about –5% and 10% respectively compared with these under "general" condition. Moreover, it is shown there are significant increases of the mean value under different road roughness grades, but the increases tend to be slight for the 95% quantile value and the maximum value, and this is because when the load intensity increases the dynamic responses of the bridge will be smaller. Nevertheless, the comparisons highlight the necessary consideration of pavement condition on the in-service performance of the bridge. However, since the studied case is a long-span bridge, its pavement condition would be highly regarded in general. Therefore, an adverse "general" pavement condition is only considered in the following analysis of lifetime girder deflections under traffic loading.
5.4. Extreme girder deflection prediction
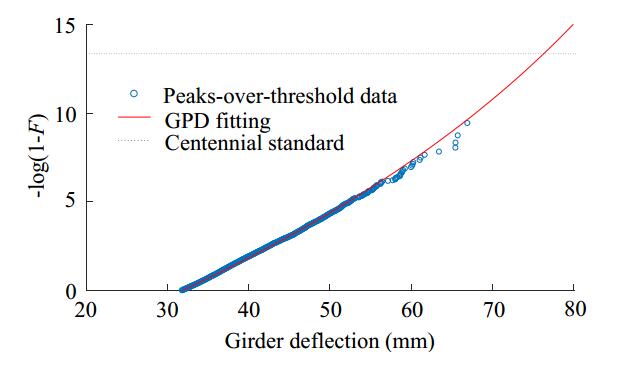
In the evaluation of vehicle driving comfort over bridges, the maximum girder deflection is generally of great concern. It is required that the calculated girder deflection under random traffic loading should be within a tolerable range, therefore the extreme value analysis of girder deflection is needed. In traffic-bridge coupling vibration analysis, time-history of 600-day girder deflections are obtained. Herein, the generalized Pareto distribution modeling based on peaks-over-threshold theory is employed for extreme extrapolation. The local maxima of girder deflections are selected to form the underlying data for extrapolation.
Figure 9 presents the extrapolation of peaks-over-threshold, where the mid-girder deflections are used as an example. Through iterative analysis, it is found 31.8mm is the optimal threshold, and then the shape and scale parameters are estimated by the maximum likelihood method being ξ = –0.0531 and σ = 4.6604 mm. The distribution of these peaks-over-threshold values and the GPD fitting model are drawn on the figure. It can be seen that the GPD model well captures the tail trend of these data, so it is believed that it can accurately predict the extreme girder deflection under any given reference period. Since the design period of the bridge is 100 years, the return period of the extreme girder deflection is assumed to be 100 years, and therefore the predicted maximum mid-span girder deflection is 78.2 mm. This deflection value is a tolerable limit under normal traffic loading. If realistic monitored girder deflection induced by normal traffic loading exceeds this tolerable limit, it indicated the traffic stream involved many overloading trucks or the bridge has suffered significant degradation, which should be warned for the bridge managers. Moreover, the estimated parameters and predicted extreme values of the three girder deflection indicators are shown in Table 4.
5.5. Warning of bridge operation
It is known the centennial deflections of the mid-span, secondary mid-span, and side mid-span are 78.2 mm, 46.9 mm, and 23.4 mm, respectively. The traffic load model specified in the Chinese bridge design code is used to analyze the girder deflections, which are 110.4 mm, 52.4 mm, and 30.1 mm respectively. Consequently, a grading deflection warning values of the studied bridge under traffic loading are shown in Table 5, which mainly focuses on the down-warping effect of the bridge. The red warning indicates it is very dangerous for the bridge, reinforcement or close the bridge to traffic should be implemented, where the tolerable value is the result calculated by the traffic load model defined in the specification. The orange warning means it is serious for the bridge structure, and relative maintenance work should be performed, where the tolerable value is the predicted centennial deflection. The yellow warning shows the bridge has a great risk that there are abnormal trucks or structure damaged, and the 90% of predicted centennial deflection is used as the tolerable value. The blue warning means the operation of the bridge is normal, and the maximal girder deflections are the 90% of predicted centennial values. Therefore, in the evaluation of bridge performance, the following grading warning values are used for analysis. If the realistic exceeds the corresponding warning value, it indicates that the bridge has been degraded significantly, or there are many overloading trucks traveling across the bridge.
6.
Conclusions
This paper studied the deflection characteristics of long-span girder bridges from the perspective of coupling vibration of stochastic traffic stream and bridge. First, a coupling vibration equation of stochastic traffic stream and bridge was established; Second, a generalized Pareto distribution extreme extrapolation method was formed based on peaks-over-threshold theory, which is used to predict the extreme girder deflections induced by the dynamic traffic loading; third, a cellular automaton based microscopic traffic stream simulation was established, and the intelligent driver car-following model and acceptable distance lane-changing model were used; finally, integrated with a prestressed continuous girder bridge, the girder deflections under the action of normal traffic stream was analyzed, which then formed a grading warning system on bridge girder deflection. The main findings are as below:
(1) The generalized Pareto distribution extrapolation method based on peaks-over-threshold theory makes better use of underlying data, which is very efficient for the prediction of traffic load effects.
(2) Based on the cellular automaton method, a microscopic traffic stream simulation approach was built using the intelligent driver car-following model and acceptable distance lane-changing model, which can simulate the on-bridge random traffic loads for any given traffic conditions.
(3) The studied case indicates that the deflections of long-span girder bridge under the action of the coupling vibration of stochastic traffic stream and bridge display a transient-state change rule, and are influenced by the pavement condition (road roughness). Through extrema extrapolation, it is discovered that the extreme girder deflections become truncated in long reference periods, demonstrating that girder deflections in normal traffic condition are limited.
(4) A grading warning system on girder deflections is proposed with red (danger), orange (serious), yellow (little serious), and blue (normal) being the four grades. If the girder deflections under dynamic traffic loading exceed the corresponding limit, it indicates that the bridge has been degraded significantly, or there are many abnormal overloading trucks traveling across the bridge. Therefore, reinforcement and maintenance should be implemented on the bridge.
Acknowledgments
This research was funded by National Natural Science Foundation of China (No. 51808148 and No. 51478192); Science and Technology Program of Guangzhou, China (No. 20190401010188). The authors gratefully acknowledge these generous supports.
Conflict of Interest
All authors declare no conflict of interest in this paper.









 DownLoad:
DownLoad: