1. Introduction
Hepatitis B virus (HBV) infection is an important global health problem implicated in liver cancer and cirrhosis. Nearly 2 billion people worldwide have been infected and 240 million patients have suffered from chronic HBV infection. Eighty percent of all liver cancer is caused by chronic hepatitis B, resulting in half a million fatalities annually [22]. Several therapeutic agents have been approved by the Food and Drug Administration, including interferon and nucleosides/nucleotides analogues (NUCs) such as lamivudine, adefovir, entecavir, telbivudine and tenofovir [1,2,13]. These agents fall into one of two categories: inhibiting de novo infection and inhibiting viral production. Despite the success of these drugs in reducing liver damage and delaying the progression of liver disease in chronically infected people, their long-term use comes with substantial complications. A critical challenge in the treatment of patients with chronic Hepatitis B is the emergence of drug resistance. In addition, high drug cost and complicated drug regimens impose a burden on some patients who have limited access to antiviral agents in developing countries [1].
Mathematical models have recently contributed significantly to understanding many complex biological systems and investigating the dynamics and control of virus such as human immunodeficiency virus (HIV) and hepatitis C virus. Many researchers have used mathematical models to simulate the course of virus infection and predict the potential response to different therapies [10,18]. They also have applied optimal control techniques with mathematical models to suggest optimal treatment strategies for HIV, tuberculosis, and vector-borne diseases [3,4,17]. Several studies have explored the optimization of strategies for vaccination distribution for influenza using control theory [15,16]. A mathematical model was developed to estimate the effects of pre-exposure prophylaxis (PrEP) on the HIV epidemic in South Korea [14].
Optimal control of HBV infection is the subject of research interest because it may contribute to the development of effective treatment strategies. The effectiveness of HBV therapy may be improved by developing dynamic drug strategies, where the treatment schedule changes over time in response to the individual's disease progression. The model we use to derive the optimal drug treatment strategies for HBV infection is originally developed in [13], although the paper did not provide a mathematical analysis of the model. The authors introduced immune effectors as a new compartment in the model to show triphasic viral dynamics since traditional biphasic models is not sufficient to explain long-term viral dynamics of hepatitis B. In this paper, we first perform a qualitative analysis of the HBV model and then consider feedback control of HBV infection incorporating current knowledge of patients. The reproduction number is determined and the stability of the steady state is investigated by using the number which is commonly used to measure the potential for the disease spread in epidemiology. We also derive optimal treatment strategies for HBV infection by formulating a feedback control problem. The model predictive control (MPC) is an advanced feedback control methodology which solves a finite-horizon open-loop control problem iteratively such that the current state is measured at the sampling time [12]. Application of the MPC method requires full information on the current state. In a clinical setting, however, it is impossible to quantify all state variables because of a lack of technical skills. To overcome the imperfection of the observation data, we use the ensemble Kalman filter (EnKF). EnKF is a recursive algorithm that produces estimates of the optimal state of the nonlinear system by using a series of observed data with noise [7,8].
A differential evolution (DE) algorithm is employed to derive the piecewise constant drug schedule, where the current state is sampled at several measurement times. DE, introduced by Price and Storn, is a population-based direct-search global optimization algorithm. In the evolutionary computation, a population of candidate solutions, called agents, iteratively progresses towards the optimum with regard to a given measure of quality. These agents are moved around in the search-space by perturbations using three main steps of mutation, crossover and selection [21,Section 2.1,page 37-47].
The rest of this paper is organized as follows: Section 2 introduces and analyzes a mathematical model describing the dynamics of HBV and immune response during antiviral therapy. The section derives the reproduction number and investigates the stability of the steady state. Section 3 formulates a feedback control problem based on EnKF and DE to derive optimal drug treatment strategies for HBV infection. The section addresses EnKF to estimate full information of the state at sampling time from partial observation data and the DE to derive an optimal piecewise constant control. Section 4 presents the results of numerical simulations with various weights in the objective functional. Section 5 concludes.
2. Model analysis
The system of ordinary differential equations describing the compartmental HBV infection dynamics is given by
|
dTdt=S−dTT−(1−η⋅μ1(t))bVT+αfIEdIdt=(1−η⋅μ1(t))bVT+mI−dII−αIEdVdt=(1−ϵ⋅μ2(t))pI−cVdEdt=SE+BEIE(I+KE)−DEE
|
(1)
|
where the four state variables T, I, V, and E represent the number of uninfected or target cells, infected cells, virus load, and immune effectors, respectively.
Target cells are assumed to be produced at the constant rate S. Target cells die at rate dTT and become infected at the rate bVT, where b is a new infection rate of target cells. New infection with HBV is blocked by treatment with NUCs, nucleoside analogues. The parameter η represents the efficacy of the treatment. Thus, the infection rate is reduced to (1−ημ1)bVT where 0≤η≤1.
Infected cells are produced at the rate of (1−ημ1)bVT and divide by mitosis at the rate of mI, where m is the mitotic production rate of infected cells. Infected cells die at rate dII and are cleared by immune effector at rate αIE, where the immune effector-induced clearance rate of the infected cells is represented as α in the equation of the infected cell. The mechanism for immune effectors involves cytolytic and noncytolytic activities. Immune effectors are thought to perform noncytolytic activity, probably causing noncytolytic, cytokine-induced curing? of infected cells [11,20]. Although there is currently no way to measure noncytolytic immune activity during HBV infection, it was assumed that the scale of noncytolytic activity is related to the scale of cytolytic activity. Therefore, noncytolytic activity was expressed using α with a calibration coefficient f in the first equation of the system where 0≤f≤1.
Free virions are assumed to be produced from infected cells at the rate of pI. The treatment of inhibiting viral production is introduced to reduce the rate by a factor of (1−ϵμ2), where ϵ denotes the efficacy of the treatment. Then, HBV is produced at the reduced rate of (1−ϵμ2)pI where 0≤ϵ≤1 and die at the rate of cV. The immune effectors are produced at the constant rate SE and die at the rate DEE. The immune effectors are stimulated at the rate of BEIEI+KE, where BE is the maximum birth rate for immune effectors and KE is the Michaelis constant. That is, the stimulation of immune response is assumed to be similar to Michaelis-Menten kinetics.
The control variables μ1(t) and μ2(t) represent time-dependent drug treatments of inhibiting de novo infection and viral production satisfying 0≤μi(t)≤1, (i=1,2), respectively. We assume that μi(t)=0 and μi(t)=1, (i=1,2) represent no-and full treatment scenarios, respectively. For simplicity of notation in the qualitative analysis, we assume that μ1(t)≡1 and μ2(t)≡1 in this section. The mathematical model (1) contains many parameters that have to be assigned before numerical simulations. The descriptions and values for the parameters are summarized in Table 1. For a more detailed discussion of this model and parameter values, see [13].
Table 1. Parameters used in the model (1). They are principally extracted from Kim et al. [13].
| Description | value | units |
| S | production rate of target cells | 5×105 | cellsmL⋅day |
| dT | death rate of target cells | 0.003 | 1day |
| η | treatment efficacy of inhibiting de novo infection | ∈[0,1] | ⋅ |
| b | de novo infection rate of target cells | 4×10−10 | mLvirions⋅day |
| f | calibration coefficient of α for target cells | 0.1 | ⋅ |
| m | mitotic production rate of infected cells | 0.003 | 1day |
| dI | death rate of infected cells | 0.043 | 1day |
| α | immune effector-induced clearance rate of infected cells | 7×10−4 | mLcells⋅day |
| ϵ | treatment efficacy of inhibiting viral production | ∈[0,1] | ⋅ |
| p | viral production rate by infected cells | 6.24 | virionscells⋅day |
| c | clearance rate of free virions | 0.7 | 1day |
| SE | production rate of immune effectors | 9.33 | cellsmL⋅day |
| BE | maximum birth rate for immune effectors | 0.5 | 1day |
| KE | Michaelis-Menten type coefficient for immune effectors | 4.07×105 | cellsmL |
| DE | death rate of immune effectors | 0.52 | 1day |
For any biological model to be feasible, it is essential that all states of the model must remain non-negative. A mathematical analysis of the model should include verification of this property. We begin by defining a domain Ω for the HBV model (1) and making assumptions for some parameters.
|
Ω={(T,I,V,E)∈R4+|0≤T+I≤SD,0≤V≤(1−ϵ)pScD,0≤E≤SEDE−BE},
|
where D=min(dT,dI−m).
Assumptions:
A1: The mitotic production rate of infected cells is smaller than the death rate of infected cells, i.e. m<dI.
A2: The maximum birth rate for immune effectors is smaller than the death rate of immune effectors, i.e. BE<DE.
Theorem 2.1. Assume that A1 and A2 hold, then Ω is positively invariant under the system (1).
Proof. Note that the states T, I, V, and E decrease only in proportion to their present sizes, and thus, all states remain nonnegative if their initial values are nonnegative.
Adding the first two equations in the model (1), we obtain
|
ddt(T+I)=S−dTT+mI−dII−αIE(1−f)≤S−dTT−(dI−m)I≤S−D(T+I),
|
where D=min(dT,dI−m). Clearly T(t)+I(t)≤SD for all t when initial value T0+I0≤SD. Similarly, we have V(t)≤(1−ϵ)pScD and E(t)≤SEDE−BE for all t. Therefore, Ω is positively invariant under the system (1)
Now we analyze the stability of the steady states by calculating the reproduction number. In epidemiology, the basic reproduction number, R0, is defined as the average number of secondary infections generated by a typical primary infection in a susceptible population. It is used to determine whether or not a disease can spread through the population. In this paper, the R0 is considered as the expected number of target cells infected through viruses reproduced by a single infected cell. It is a key threshold quantity for conducting qualitative analysis of the model. Because the model (1) include treatment, we speak of a control reproduction number Rc rather than a basic reproduction number R0. If there is no treatment (μ1(t)=0, μ2(t)=0), then Rc reduces to R0.?
Clearly, the HBV model (1) has a unique virus-free equilibrium given by
Using the next generation approach [6,page 230], we calculate Rc, which is critical to the stability of the virus-free equilibrium. To this end, we split the HBV model (1) into two systems with a disease compartment x=(I,V)t and a non-disease compartment y=(T,E)t as
|
dxdt=F−V and dydt=[S−dTT−(1−η)bVT+αfIESE+BEIE(I+KE)−DEE],
|
where
|
F=[(1−η)bVT0]andV=[(dI−m+αE)I−(1−ϵ)pI+cV].
|
The linearized equations for the disease compartment, x, at the virus-free equilibrium can be written as
where
|
F=∂F∂x=[0(1−η)bSdT00]andV=∂V∂x=[dI−m+αSEDE0−(1−ϵ)pc].
|
Then Rc is given by
|
Rc=ρ(FV−1)=(1−η)bS(1−ϵ)pcdT(dI−m+αSEDE),
|
(2)
|
where ρ(A) denotes the spectral radius of a matrix A.
Theorem 2.2. Assume that A1 and A2 hold. The virus-free equilibrium, EQ0 for the system (1) is locally asymptotically stable if Rc<1 and unstable if Rc>1.
Proof. At the virus-free equilibrium, the Jacobian matrix of the system (1) is
|
J(EQ0)=[−dTαfSEDE−(1−η)bSdT00(m−dI−αSEDE)(1−η)bSdT00(1−ϵ)p−c00BESEKEDE0−DE].
|
And the characteristic polynomial of the Jacobian matrix is given by
|
p(λ)=(−dT−λ)(−DE−λ)((m−dI−αSEDE−λ)(−c−λ)−(1−ϵ)p(1−η)bSdT).
|
Clearly, λ1=−dT,λ2=−DE are two of the eigenvalues of the Jacobian matrix. Denote λ3 and λ4 as the other eigenvalues. These values are the roots of the quadratic polynomial in p(λ) given by
|
(m−dI−αSEDE−λ)(−c−λ)−(1−ϵ)p(1−η)bSdT=λ2−(m−dI−αSEDE−c)λ+(m−dI−αSEDE)(−c)−(1−ϵ)p(1−η)bSdT.
|
So we have
|
λ3+λ4=m−dI−αSEDE−c,λ3λ4=(m−dI−αSEDE)(−c)−(1−ϵ)p(1−η)bSdT=(dI−m+αSEDE)c(1−Rc).
|
By assumption A1, we have λ3+λ4<0. Therefore, all of the eigenvalues of the Jacobian matrix have negative real parts when Rc<1. However, not all roots of this polynomial can have negative real parts when Rc>1. This means that the virus-free equilibrium is locally asymptotically stable when Rc<1 and unstable when Rc>1.
We note that the global stability of the virus-free equilibrium can be established by verifying the conditions of the global stability theorem in [5,page 176]. Consider the abstract form of a mathematical model to introduce the theorem:
|
x′=−Ax−ˆf(x,y)y′=g(x,y)
|
(3)
|
where x denotes a disease compartment and y denotes a non-disease compartment.
Definition 2.3. A is called M-matrix if and only if there exists a matrix B≥0 and a real number r≥ρ(B) such that A=rI−B.
Remark 1. [9] A is a M-matrix if and only if A is a real nonsingular matrix such that aij≤0 for all i≠j and each entry of A−1 is nonnegative.
We now assume that y∗ is a globally asymptotically stable equilibrium of y′=g(0,y).
Theorem 2.4. [5,page 176] If A is a nonsingular M-matrix and ˆf≥0, then (0,y∗) is a globally asymptotically stable equilibrium of (3).
Theorem 2.5. Assume that A1 and A2 hold. If Rc<1, then the virus-free equilibrium, EQ0, is globally asymptotically stable when E(0)>SEDE and dT≤dI−m.
Proof. Our model can be written as
|
x′=−Ax−ˆf(x,y)y′=g(x,y)=[S−dTT−(1−η)bVT+αfIESE+BEIE(I+KE)−DEE],
|
(4)
|
where
|
A=[−(m−dI−αSEDE)−(1−η)bSdT−(1−ϵ)pc],
|
|
ˆf(x,y)=[(1−η)bV(SdT−T)+αI(E−SEDE)0].
|
It is clear that y∗=(SdT,SEDE) is a globally asymptotically stable equilibrium of y′=g(0,y) and a12 and a21 in the matrix A are nonpositive.
Now consider the inverse of A,
|
A−1=1(dI−m+αSEDE)c(1−Rc)[c(1−η)bSdT(1−ϵ)pdI−m+αSEDE].
|
Thus A is M-matrix when Rc<1 by Remark 1.
In addition, E≥SEDE when E(0)>SEDE because of the form of the fourth equation in our model (1) and T≤SdT when dT≤dI−m by Theorem 2.1. That is, ˆf(x,y)≥0. Therefore, the virus-free equilibrium, EQ0, is globally asymptotically stable when E(0)>SEDE and dT≤dI−m by Theorem 2.4.
Theorem 2.6. Suppose that assumptions A1 and A2 hold. There exists a unique positive chronic equilibrium if Rc>1 and there is no chronic equilibrium if Rc<1.
Proof. To determine a chronic equilibrium, (T∗,I∗,V∗,E∗), the following equations are solved:
|
S−dTT∗−(1−η)bV∗T∗+αfI∗E∗=0(1−η)bV∗T∗+mI∗−dII∗−αI∗E∗=0
|
(5)
|
|
SE+BEI∗E∗I∗+KE−DEE∗=0
|
(7)
|
By the third and fourth equations, we have
|
V∗=I∗(1−ϵ)pc , E∗=−SE(I∗+KE)I∗(BE−DE)−KEDE.
|
Substituting V∗ and E∗ in the first equation
|
T∗=S+αfI∗E∗dT+(1−η)bV∗=S+αfI∗−SE(I∗+KE)I∗(BE−DE)−KEDEdT+(1−η)bI∗(1−ϵ)pc.
|
(8)
|
By the second equation and the above expression, we finally obtain a quadratic polynomial, P(I∗);
|
P(I∗)=(1−η)b(1−ϵ)p(S(I∗(BE−DE)−KEDE)−I∗αfSE(I∗+KE))+(m−DI)(cdT+I∗(1−η)b(1−ϵ)p)(I∗(BE−DE)−KEDE)+αSE(I∗+KE)(cdT+I∗(1−η)b(1−ϵ)p)=AI∗2+BI∗+C=0
|
where
|
A=(m−dI)(1−η)b(1−ϵ)p(BE−DE)+αSE(1−f)(1−η)b(1−ϵ)pB=(1−η)b(1−ϵ)p(S(BE−DE)−αfSEKE)+(m−dI)cdT(BE−DE)−(m−dI)(1−η)b(1−ϵ)pKEDE+αSEKE(1−η)b(1−ϵ)p+αSEdTC=−(1−η)b(1−ϵ)pSKEDE+αSEKEcdT−(m−dI)cdTKEDE=KE((−m+dI)DE+αSE)cdT(1−Rc)
|
By our assumptions, A>0. And C<0 if Rc>1. This means there exists only one positive root of P(I∗) and thus a corresponding chronic equilibrium, EQ∗=(T∗,I∗,V∗,E∗) if Rc>1. On the other hand, there is no chronic equilibrium if Rc<1.
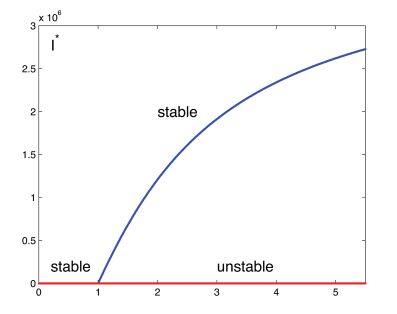
A general qualitative analysis of our model is very challenging due to the high nonlinearities in our model. However, we are still interested in the stability of the steady state, so we conducted a stability analysis of the steady state numerically. Given the parameter values in Table 1, we plot the bifurcation diagram of the model system (1) with varying ϵ and η=0.5. In Figure 1, the x− and y−axes stand for Rc and the steady state I∗, respectively. By checking the eigenvalues of Jacobian, we verify that the virus-free steady state is locally asymptotically stable when Rc<1 and it is unstable when Rc>1. Moreover, our simulation supports that there exists a chronic equilibrium which is locally asymptotically stable when Rc>1.
3. Feedback control
One of the study goals is to design optimal drug treatment strategies using mathematical models and control techniques. One way to achieve this goal is to consider an optimal control problem minimizing the number of virions with consideration for the treatment costs. Thus, we define the objective functional as
|
J(μ1,μ2)=∫w1⋅V(t)+w2⋅μ21(t)+w3⋅μ22(t)dt
|
(9)
|
The weight constants wi, (i=1,2,3) can be chosen to balance the relative costs of the virus load V and control efforts of μ1(t) and μ2(t). Then we formulate an optimal control problem to minimize the objective functional constrained to the dynamics of the HBV infection:
|
minimize J(μ1,μ2) subject to (1).
|
In our optimal control formulation, the MPC method is used in order to reflect the status of patients at both initial time and follow-up visits. Therapy strategies are determined based on the current state of the system at each sampling time, which is the initial state for the open-loop control problem in each subinterval. In order to formulate the MPC, we assume that the current state is measured at ti where ti<ti+1 and Ti is the control horizon time such that ti+1≤ti+Ti for i=0,1,2,⋯. The MPC algorithm proceeds as follows:
1. Solve the open-loop optimal control problem minimizing the objective functional (9) in the interval [ti,ti+Ti] with the initial value x(ti)=xi,
2. Determine the state x(t) in the interval [ti,ti+Ti] by solving the model (1) with the derived optimal control functions,
3. Determine xi+1 by using measured data and the predicted state x(t) at t=ti+1,
4. Repeat this process over the next time interval [ti+1,ti+1+Ti+1] with initial value x(ti+1)=xi+1.
There are several technical issues to be addressed to implement our approach. Synthesis of the nonlinear feedback control requires full knowledge of all the state variables. However, in a clinical setting, only partial information of the state is given due to lack of technical skill to quantify all the state variables. The ideas of the Kalman filter (KF) are employed to design a state estimator. Then we are interested in restricted class of piecewise constant controllers that are usual treatment protocols in practice. DE, an algorithm that optimizes a problem by iteratively improving a candidate solution, has a great potential as a tool for deriving piecewise constant strategies.
In this section, we give a brief summary of two main techniques, KF and DE, used in the MPC. We begin with the basic ideas and background of KF and move to modified algorithms to take care of nonlinearity and the system with continuous dynamics and discrete measurements. In the second part, the DE method is introduced and each step is explained with illustrations.
Figure 2 shows how these techniques are incorporated to solve a control problem to yield an efficient treatment strategy.
3.1. Hybrid ensemble Kalman filter (EnKF)
Kalman filter (KF) uses a series of measurements observed over time containing noise and produces estimates of state variables by a combination of the probability distribution from the model prediction and the measurement. It is a recursive algorithm that only utilizes the first two moments of the state, mean and covariance, to characterize the entire optimal estimate for linear systems with additive Gaussian noise in both the process model and the observation. Consider a linear, discrete system of dynamics and measurement:
|
xk=Fk−1xk−1+wk−1zk=Hkxk+vk
|
(10)
|
where xk is a state vector, Fk the state transition model, and Hk the observation model which maps the true state xk into the observation zk. There are several assumptions for KF regarding noise terms in process and measurement models. The initial state x0 is a Gaussian with a known mean ˉx0 and a covariance matrix P0. Noise wk and vk are assumed to be zero-mean Gaussian processes with covariances Qk and Rk, respectively.
The KF algorithm consists of a prior step to predict by the process model and a posterior step to update based on the measurement, which can be summarized as
• Prior estimation (prediction):
|
ˆx−k=Fk−1ˆxk−1P−k=Fk−1Pk−1FTk−1+Qk−1
|
• Posterior estimation (update):
|
K=P−kHTk(HkP−kHTk+Rk)−1ˆxk=ˆx−k+K(zk−Hkˆx−k)Pk=(I−KHk)P−k
|
The probability distribution of state variables in a linear model is completely characterized by its mean and covariance for all times if the initial condition follows a normal distribution. For a nonlinear model, however, the first two moments of the state will not characterize the full probability density, but do determine the mean path and the dispersion about that path. A number of extensions have been proposed to deal with nonlinear dynamics. We also note that physical systems are often represented as continuous-time dynamics in conjunction with discrete-time measurements.
|
˙x(t)=f(x,t)+w(t)zk=Hkxk+vk
|
(11)
|
The extended Kalman filter approximates the nonlinear dynamics model by a linearization about the current state. This linear model is then propagated forward under the basic KF algorithm and is used to approximate the optimal mean and covariance for the state of the system. It has been observed that the extended Kalman filter may fail to achieve meaningful results, in the case of large nonlinearity or poor initial guess. Another set of approaches based on sampling techniques have been developed, as opposed to deterministic ones, to characterize the distributions. One such approach, EnKF, generates numerous points sampled from the assumed distribution and propagates them forward to calculate the mean and variance of these samples [8,page 38-46]. Adjustments have to be made to account for nonlinearity and discrepancy in time. In this particular problem, we only shows the numerical results obtained by applying EnKF because the results of both EKF and EnKF algorithms are consistent. The hybrid version EnKF algorithm is given as follows:
• Initialize: Generate particles X={x0,j} sampled from initial distribution
|
ˆx(0)=E[x0,j]P(0)=E[(x0,j−E[x0,j])(x0,j−E[x0,j])T]
|
• Prior estimation (prediction):
|
X−={x−k,j|˙x−k,j=f(x−k,j,t)+w(t) with initial values xk−1,j∈X}ˆx−=E[X−]P−=Cov[X−,X−]
|
• Posterior estimation (update):
|
Z−={z−k,j=Hkx−k,j}Z={zk,j=zk+vk,j}K=Cov[X−,Z−]⋅(Cov[Z−,Z−]+Cov[Z,Z])−1X={xk,j=x−k,j+K(zk,j−z−k,j)}ˆxk=E[X]Pk=Cov[X,X]
|
In order to apply the KF technique, we introduce the notation x and r to denote the state and control vectors, respectively. Thus we define
With the above notation, the HBV model (1) can be expressed in the form
For feedback control, we need current knowledge on the state of the system. We assume that partial state observation of viral load V is available, which is representative of the type of data in a clinical setting. Hence, the measurement or observation takes the form
3.2. Differential evolution (DE) method
DE is a direct-search global optimization algorithm that was originally developed by Price and Storn in 1997. Let J:RD→R be the cost functional to be minimized. The DE algorithm can then be described as follows:
Step 1. Initialization The initial population of possible candidate vectors {xi:i=1,2,..,Np} are generated by random sampling in the search-space. Each element of a candidate vector of dimension D is denoted by xi=[xi,j:j=1,2,...,D].
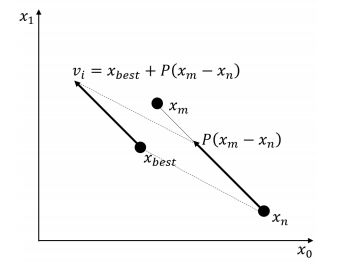
Step2. Mutation Mutant vectors {vi} are generated according to
|
vi=xbest+P(xm−xn)i=1,2,...,Np
|
(12)
|
where xbest is the best candidate, {xm,xn} are two distinct arbitrary candidate solution vectors and P∈(0,2) is a mutation scale factor.
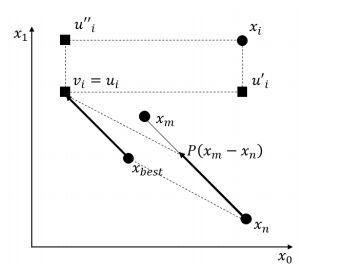
Step3. Crossover A set of vectors {ui} is formed for each i=1,2,...,Np,
|
ui,j={vi,j,if randj(0,1)≤CRxi,j,otherwise
|
(13)
|
where j=1,2,...,D and CR∈[0,1] is a crossover probability.
Step4. Selection The next generation vectors are selected as
|
xi={ui,if J(ui)<J(xi)xi,otherwise
|
(14)
|
Repeat steps 2-4 until the termination criteria are met.
DE creates mutant agents using the scaled difference of two randomly selected candidate vectors in the mutation step (Figure 3). In the algorithm, the scale factor P∈[0,2] gives the scatter around xbest and P>1 is required for a successfully optimized result, in general. The crossover step allows the construction of new candidate vectors by combining the current and mutant agents (Figure 4). CR∈[0,1], called a crossover probability, determines the extent of preference given to the mutant in recombination of components in each candidate vector. The average number of parameters mutated depends on the crossover probability and many genetic algorithms recommend a crossover probability of 1/D, where D is the dimension of a solution vector. In the selection, replace the current agent in the population if the candidate vector is an improvement.
In summary, mutation expands the search space, crossover incorporates candidate vectors from the previous generation and new candidate vectors for recombination, and selection admits the one with the best fitness to the next generation. Therefore, mutation and crossover tend to increase the diversity of a population, whereas selection reduces it. To avoid premature convergence due to the selection pressure, it is crucial to choose P and CR that are of sufficient magnitude. Selecting desirable parameters in DE has been the subject of much research, since the choice of parameters can have a large impact on optimization performance [19].
4. Numerical results
We illustrate the nonlinear feedback control incorporating EnKF and DE algorithms using synthetic data. We consider a drug treatment strategy over 200 days with monthly measurement. A set of synthetic data is constructed by adding 5% random noise to the model prediction of viral load V for every time point for the measurement. The parameters used are summarized in Table 1 and the initial values for state variables are
|
T0=1.4×108,I0=3.75×105,V0=5×108,E0=100
|
At each sampling time, an initial guess for the covariance to start the EnKF is chosen to be a diagonal matrix in which diagonal entries are 10. In the DE algorithm, the population size Np, the differential weight P, and the crossover probability CR are selected to be Np=500,P=1.1, and CR=0.7, respectively. The values of the drug efficacy for η and ϵ are set to 0.9.
To suggest general policies for efficient treatment, we run the simulations under various settings. The weight constants wi in the objective functional (9) can be chosen to balance the difference in the magnitudes and/or relative costs of the viral load and the drug treatment. In fact, the second and third terms in the objective functional (9) with weights w2 and w3 represent systemic costs of the drug treatments which mean severity of unintended side effects as well as treatment cost. In numerical simulations, weights for drug treatments w2 and w3 are varied to compare the optimal treatment strategies under different relative costs, keeping the weight for virus cells w1=10−7 fixed to balance the magnitudes.
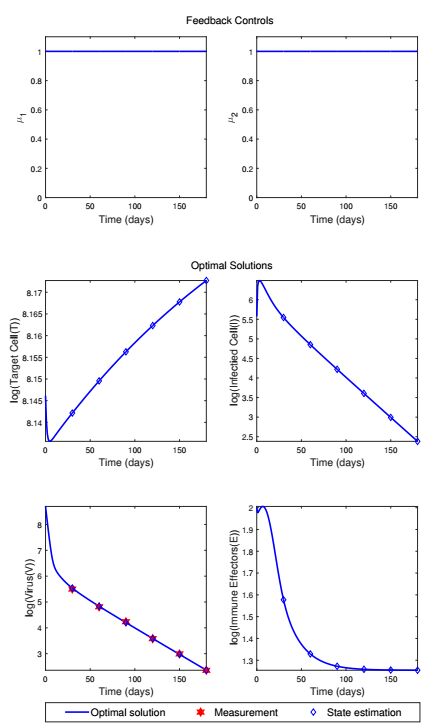
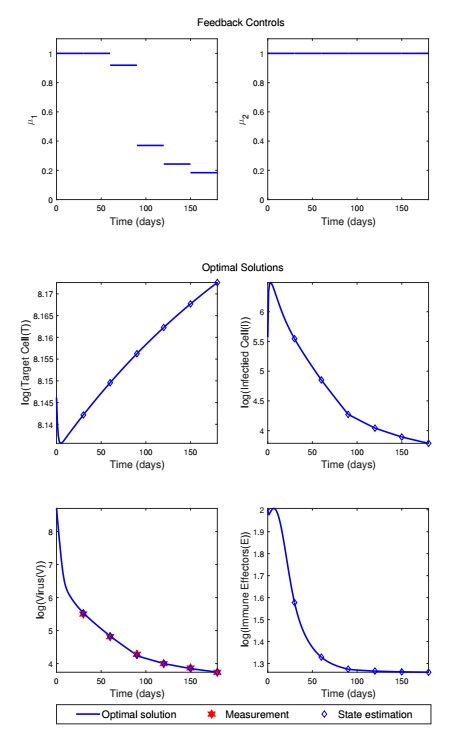
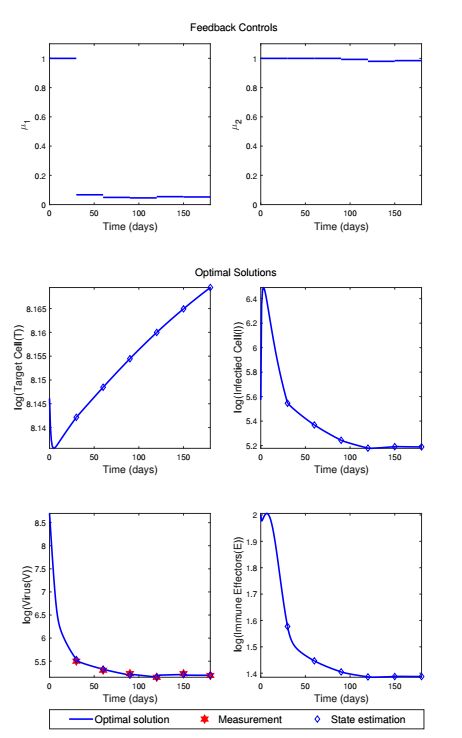
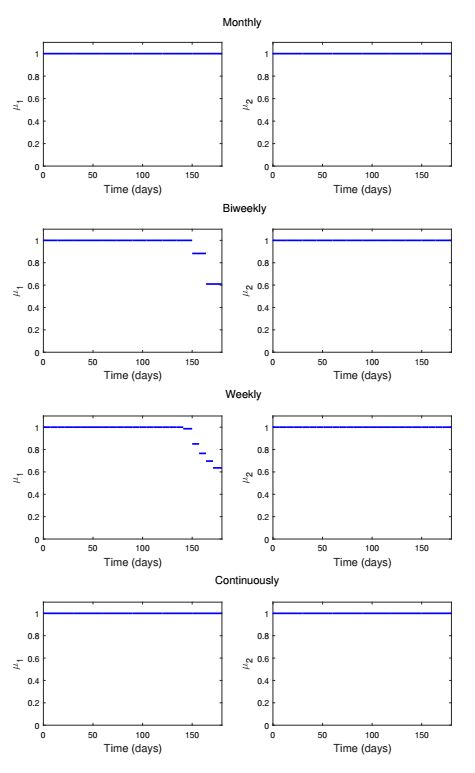
Figure 5 displays the time dependent feedback controls and the corresponding states with the choice of w2=10−5 and w3=10−5. Hybrid EnKF is used to recover the full states (diamond) from the partial measurement (star). Then the DE algorithm is followed to obtain the optimal piecewise constant functions. The derived drug schedules for both treatments are nearly identical to the full treatment in this case. That is, the maximum dosage of the both drugs are recommended for the whole duration if the systemic costs of the drug treatments are relatively low (w2=10−5 and w3=10−5). The corresponding optimal states obtained by solving the system (1) are also presented. Drug treatment causes the low viral load, which discourages an immune response.
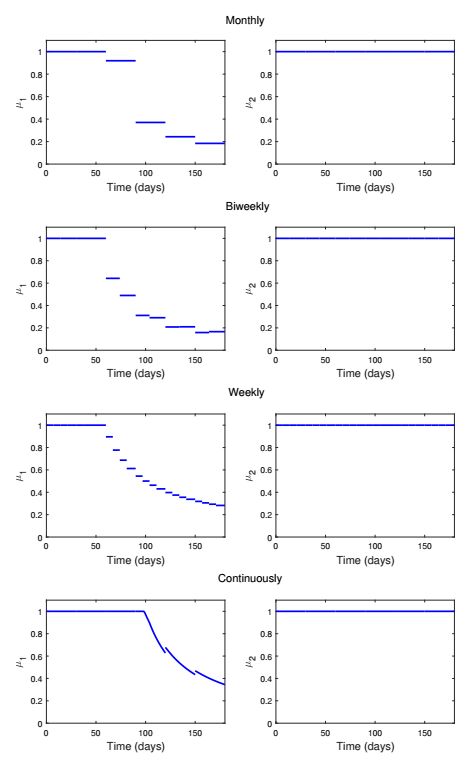
The impact of different weights on feedback control is explored by varying the weights for w2 and w3 in Figure 6 and Figure 7. The dosage of μ1 tapers off from the end of treatment duration, whereas the dosage of μ2 is maintained, as the weights for μ1 and μ2 increase simultaneously. In Figure 6, the temporal schedule of optimal control μ1 stays at full dosage for 60 days and begins to reduce until it reaches the level of 20% approximately in the end. We note that the decline in the dosage of the drug inhibiting de novo infection is closely related to the virus load. Figure 7 shows that μ1 is almost zero except in the first 30 days whereas μ2 maintains its maximum value during the whole period in the case of w2=10−1, and w3=10−1. One may conclude that μ2 is more effective than μ1 in reducing the viral load and infected cells due to underlying mechanisms when both controls have the same level of reduction in inhibition. That is, it is more efficient that some patients who have limited access to therapeutic agents due to high cost should reduce their use of drugs that inhibit de novo infection while maintaining their use of drugs that inhibit viral production.
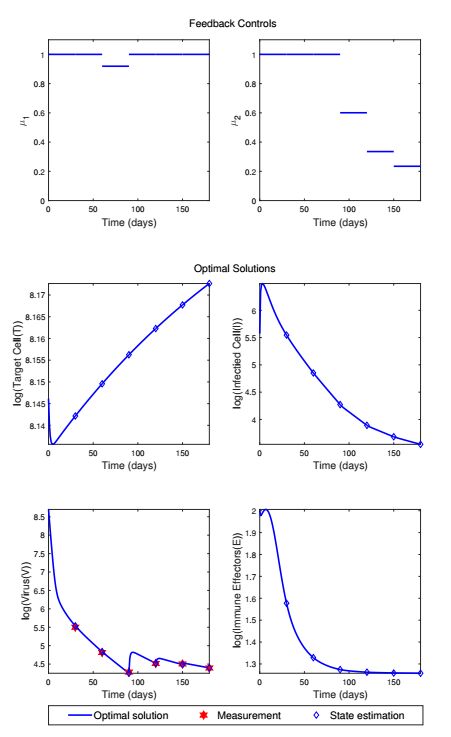
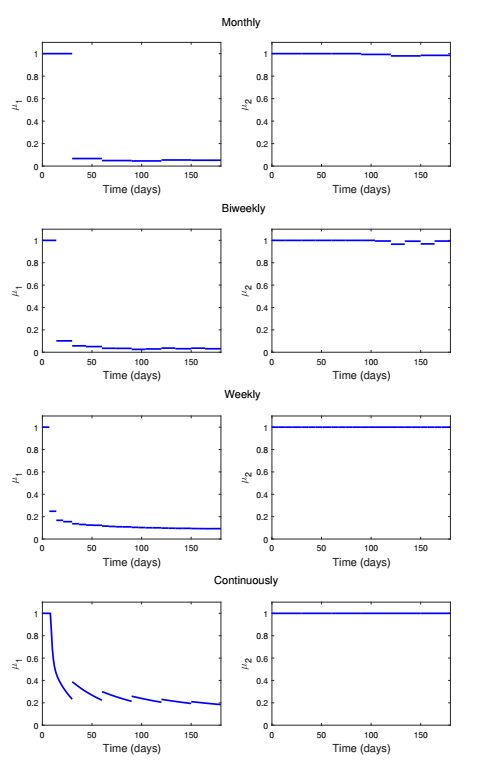
In Figure 8, w2=10−3 and w3=10−2 are chosen to consider the case when μ1 and μ2 have different costs to implement. It is observed that the dosage of μ2 maintains its maximum value up to the 90th day and then tapers off whereas the dosage of μ1 maintains its full dosage for the whole treatment duration when the cost of μ2 is higher than the cost of μ1.
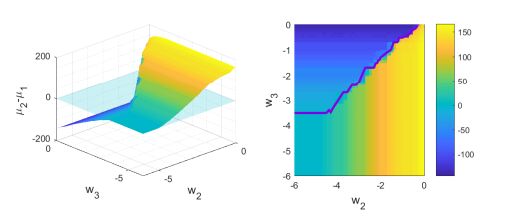
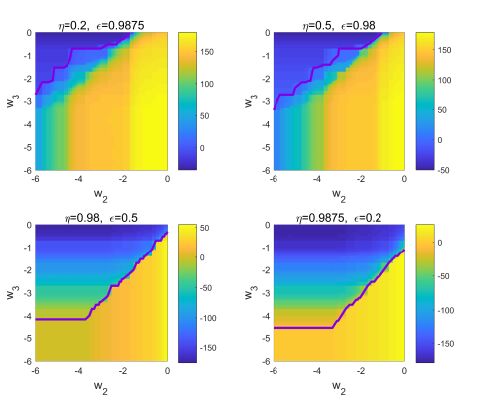
The relation between the relative dosage and the weights of two drugs are investigated further in Figure 9 and Figure 10. In the baseline case, we set efficacy of both drugs η=ϵ=0.9 and vary the weights w2 and w3 in the range [10−6,100]. To compared the total dosage of drugs that inhibit de novo infection and inhibit viral production regarding to the change of weights, the difference μ2−μ1 between the total amount of μ2 and μ1 for the whole duration is displayed in the Figure 9. Then the positive region of difference where the total dosage of μ2 is higher than μ1, is divided from the negative one by a threshold curve (solid line). As it is noticed in previous results, the case of same weights is included in the positive region because μ1 begins first to reduce its dosage when the weights increase simultaneously.
In Figure 10, simulations are performed using various combinations of treatment efficacy assuming the total efficacy of 99%. In the first row, threshold is portrayed when the efficacy of viral production inhibitor is higher than the efficacy of de novo infection inhibitor. The region where the dosage of μ2 is higher than μ1 is enlarged as the efficacy of viral production inhibitor, ϵ, increases. On the other hand, the positive region decreases if η rises as illustrated on the bottom.
We performed numerical simulations with monthly, biweekly, and weekly measurement to investigate the influence of measurement time in Figure 11-13. Optimal treatment strategies are illustrated as weights w2 and w3 increase simultaneously. We also derived piecewise continuous optimal controls to carry out comparative assessments of different treatment schedules. While the resulting strategies are slightly different in details, the general conclusions are consistent. That includes that μ2 is more effective than μ1 in reducing the viral load and infected cells assuming the same level of reduction in inhibition.
5. Conclusion
This paper formulates and analyzes a mathematical model of the HBV infection for a better understanding of the interaction between the HBV infection and the immune response during antiviral therapy. The qualitative analysis shows that the proposed model possesses one virus-free equilibrium and one chronic equilibrium with some assumptions. A detailed local/global stability analysis of the virus-free steady state is conducted using the Jacobian matrix method combined with the reproductive number. Bifurcation analysis is also performed to support our theoretical results for the stability analysis numerically.
In addition, the paper considers a feedback control problem to reflect the status at each sampling instance. The ideas of EnKF are used to address the issue of incomplete observation data. Then we apply the DE algorithm to derive piecewise constant control, which is the usual protocol in practice. The results of numerical simulations indicate that as the treatment costs increase, the drug dosage tapers off, resulting in decreased drug use. It is observed that μ2, which inhibits viral production, may be more effective than μ1, which inhibits de novo infection, in reducing the viral load assuming both controls have the same cost. However, drug dosage is a function of weight and is determined by the relative costs of drugs, in general.









 DownLoad:
DownLoad: