1. Biochemistry of the Transglutaminases
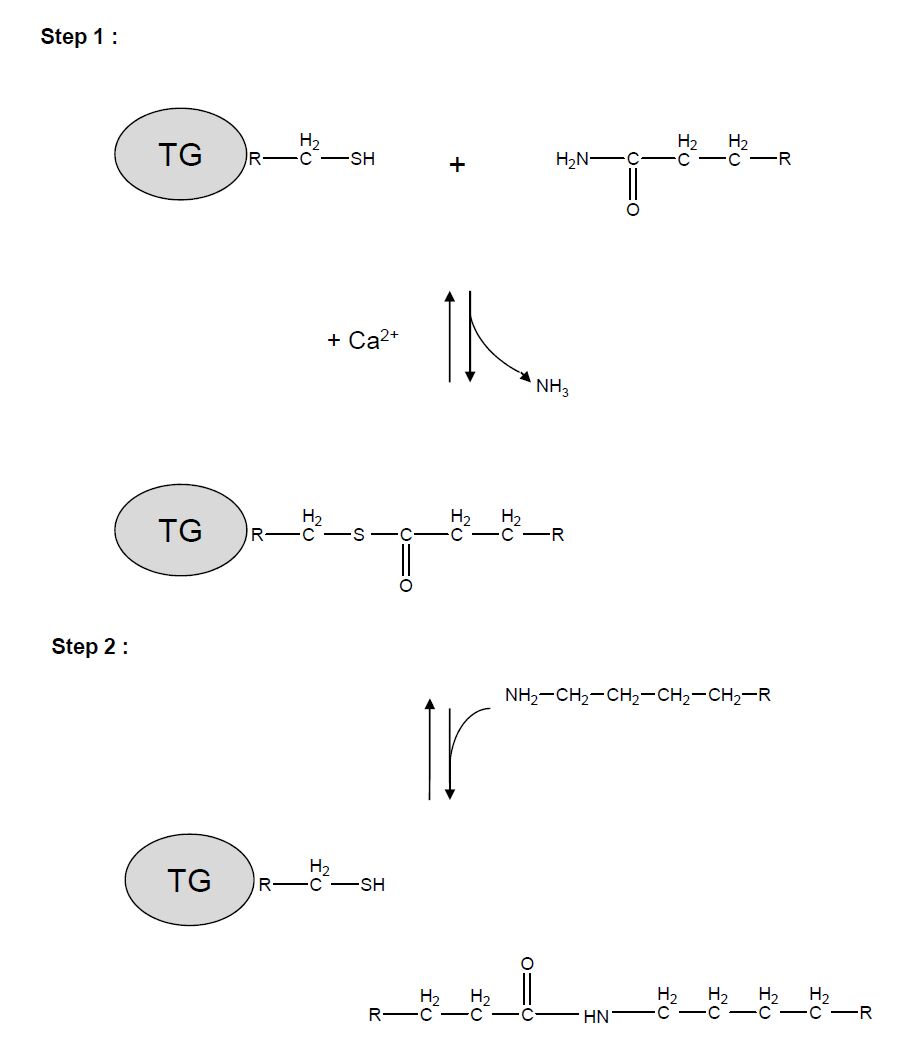
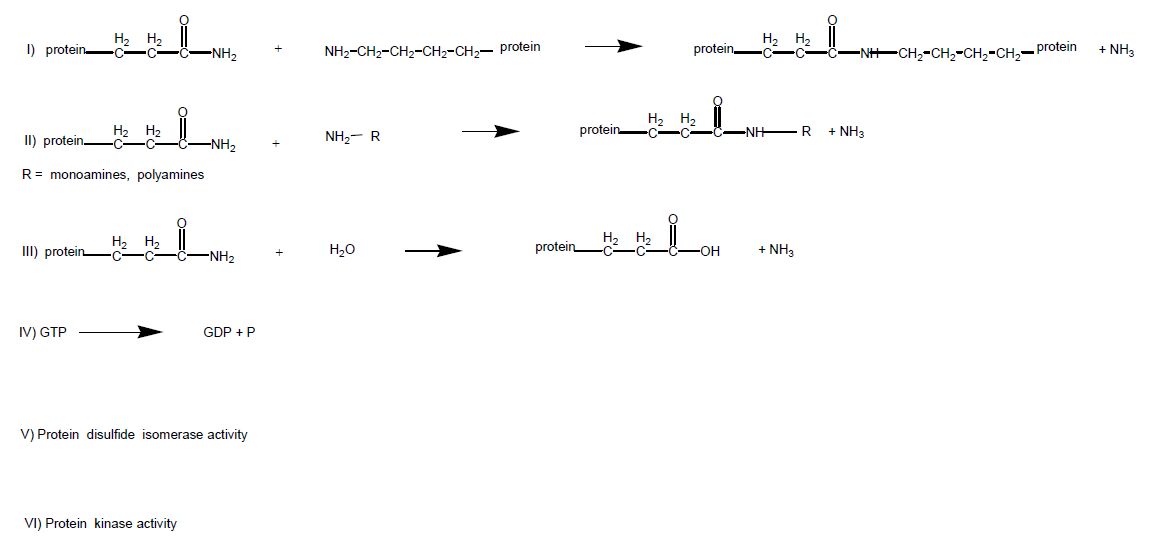
Transglutaminases (TGs, E.C. 2.3.2.13) are Ca2+-dependent enzymes that catalyze post-translational modifications of proteins. Examples of TG-catalyzed reactions include: I) acyl transfer between the γ-carboxamide group of a protein/polypeptide glutaminyl residue and the ε-amino group of a protein/polypeptide lysyl residue; II) attachment of a polyamine to the γ-carboxamide of a glutaminyl residue; III) hydrolytic deamidation of the γ-carboxamide group of a protein/polypeptide glutaminyl residue (Figure 1) [1,2]. The reactions catalyzed by TGs occur by a two-step mechanism (pinγ-pong type) (Figure 2). The transamidating activity of TGs is activated by the binding of Ca2+, which exposes an active-site cysteine residue. This cysteine residue reacts with the γ-carboxamide group of an incoming glutaminyl residue of a protein/peptide substrate to yield a thioacyl-enzyme intermediate and ammonia, (Figure 2,Step 1). The thioacyl-enzyme intermediate then reacts with a nucleophilic primary amine substrate, resulting in the covalent attachment of the amine-containing donor to the substrate glutaminyl acceptor and regeneration of the cysteinyl residue at the active site, (Figure 2,Step 2). If the primary amine is donated by the ε-amino group of a lysyl residue in a protein/polypeptide, a Nε-(γ-L-glutamyl)-L-lysine (GGEL) isopeptide bond is formed, (Figure 1,example I). On the other hand, if a polyamine or another primary amine (e.g. histamine, serotonin and others) acts as the amine donor, a γ-glutamylpolyamine (or γ-glutamylamine) residue is formed, (Figure 1,example II). It is also possible for a polyamine to act as an N, N-bis-(γ-L-glutamyl)polyamine bridge between two glutaminyl acceptor residues either on the same protein/polypeptide or between two proteins/polypeptides [3]. If there is no primary amine present, water may act as the attacking nucleophile, resulting in the deamidation of glutaminyl residues to glutamyl residues, (Figure 1,example III). It is worthwhile to note that two of these reactions, in particular, the deamidation of peptides obtained from the digestion of the gliadin, a protein present in wheat, and the Nε-(γ-L-glutamyl)-L-lysine (GGEL) isopeptide formation between these peptides and TG2 (tissue transglutaminase), have been shown to be responsible for the formation of new antigenic epitopes responsible for the Celiac disease, one of the most common human autoimmune diseases [4,5]. Regarding the physiological roles played by the transglutaminase activity, recently transglutaminase-catalyzed polyamination of tubulin has been shown to stabilize axonal microtubules, suggesting an important role for these reactions also during some physiological processes, such as neurite outgrowth and axon maturation [6]. The reactions catalyzed by TGs occur with little change in free energy and hence should theoretically be reversible. However, under physiological conditions the cross linking reactions catalyzed by TGs are usually irreversible. This irreversibility partly results from the metabolic removal of ammonia from the system and from thermodynamic considerations resulting from altered protein conformation. Some scientific reports suggest that TGs may be able to catalyze the hydrolysis of Nε-(γ-L-glutamyl)-L-lysine cross-links (GGEL) isopeptide bonds in some soluble cross-linked proteins. Furthermore, it is likely that TGs can catalyze the exchange of polyamines onto proteins [2]. In TG2 other catalytic activities, such as the ability to hydrolyze GTP (or ATP) into GDP (or ADP) and inorganic phosphate (Figure 1,example IV), a protein disulfide isomerase activity (Figure 1,example V), and a kinase activity that leads to phosphorylation of histones, retinoblastoma (RB) and P53 (Figure 1,example VI), are present, while only some of these activities have been identified also in other TGs [7,8,9].
2. Transglutaminases are Multifunctional Enzymes
Numerous lines of experimental evidence indicate that some TGs are multifunctional proteins with distinct and regulated enzymatic activities. In fact, under physiological conditions, the transamidation activity of TGs is latent [10], while other activities, recently identified, could be present. For example, in some physiological states, when the concentration of Ca2+ increases, the crosslinking activity of TGs may contribute to important biological processes. As previously described, one of the most intriguing properties of some TGs, such as TG2, is the ability to bind and hydrolyze GTP and furthermore, to bind to GTP and Ca2+. GTP and Ca2+ regulate its enzymatic activities, including protein cross-linking, in a reciprocal manner: the binding of Ca2+ inhibits GTP-binding and GTP-binding inhibits the transglutaminase cross-linking activity of the TG2 [7]. Interestingly, TG2 shows no sequence homology with heterotrimeric or low-molecular-weight G-proteins, but there is evidence that TG2 (TG2/Ghα) is involved in signal transduction, and, therefore, TG2/Ghα should also be classified as a large molecular weight G-protein. Other studies, along with ours, showed that TG2/Ghα can mediate the activation of phospholipase C (PLC) by the α1b-adrenergic receptor [11] and can modulate adenylyl cyclase activity [12]. TG2/Ghαcan also mediate the activation of the d1 isoform of PLC and of maxi-K channels [13]. Interestingly, the signaling function of TG2/Ghα is preserved even with the mutagenic inactivation of its crosslinking activity by the mutation of the active site cysteine residue [14].
3. Molecular Biology of the Transglutaminases
To date at least eight different TGs, distributed in the human body, have been identified (Table 1) [15,16,17,18,19,20]. Complex gene expression mechanisms regulate the physiological roles that these enzymes play in both the intracellular and extracellular compartments. In the Nervous System, for example, several forms of TGs are simultaneously expressed [21,22,23]. Moreover, in these last years, several alternative splice variants of TGs, mostly in the 3x-end region, have been identified [24]. Interestingly, some of them are differently expressed in human pathologies, such as Alzheimer’s Disease (AD) [25]. On the basis of their ubiquitous expression and their biological roles, we may speculate that the absence of these enzymes would be lethal. However, this does not always seem to be the case, since, for example, null mutants of the TG2 are usually phenotypically normal at birth [13,26,27]. This result may be explained by the multiple expressions of other TG genes that may substitute the TG2 missing isoform, although other TG isoform mutations have been associated to severe phenotypes, such as lamellar ichthyosis for TG1 isoform mutations. Bioinformatic studies have shown that the primary structures of human TGs share some identities in only few regions, such as the active site and the calcium binding regions. However, high sequence conservation and, therefore, a high degree of preservation of secondary structure among TG2 (transglutaminase 2), TG3 (transglutaminase 3) and FXⅢa (Factor XⅢa) indicate that these TGs all share four-domain tertiary structures which could be similar to those of other TGs [28].
Table1. TGs and their physiological roles when known.
| TG |
Physiological role |
Gene map location |
Reference |
| Factor XIIIa |
Blood clotting |
6p24-25 |
[15] |
| TG1 (Keratinocyte TG,kTG) |
Skin differentiation |
14q11.2 |
[16] |
| TG2 (Tissue TG,tTG,cTG) |
Apoptosis,cell adhesion,signal transduction,extra- cellular matrix stabilisation |
20q11-12 |
[17] |
| TG3 (Epidermal TG,eTG) |
Hair follicle differentiation |
20p11.2 |
[18] |
| TG4 (Prostate TG,pTG) |
Suppression of sperm immunogenicity |
3q21-2 |
[19] |
| TG5 (TG X) |
Epidermal differentiation |
15q15.2 |
[20] |
| TG6 (TG Y) |
Central Nervous System development |
20p13 |
[20] |
| TG7 (TG Z) |
Unknown function |
15q15.2 |
[20] |
4. Roles of the Transglutaminases in Neurodegenerative Diseases
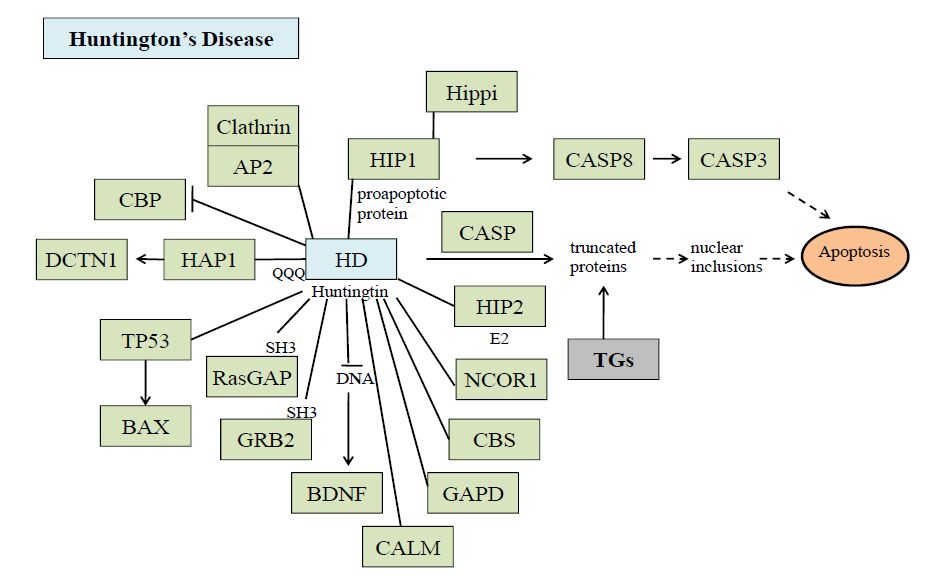
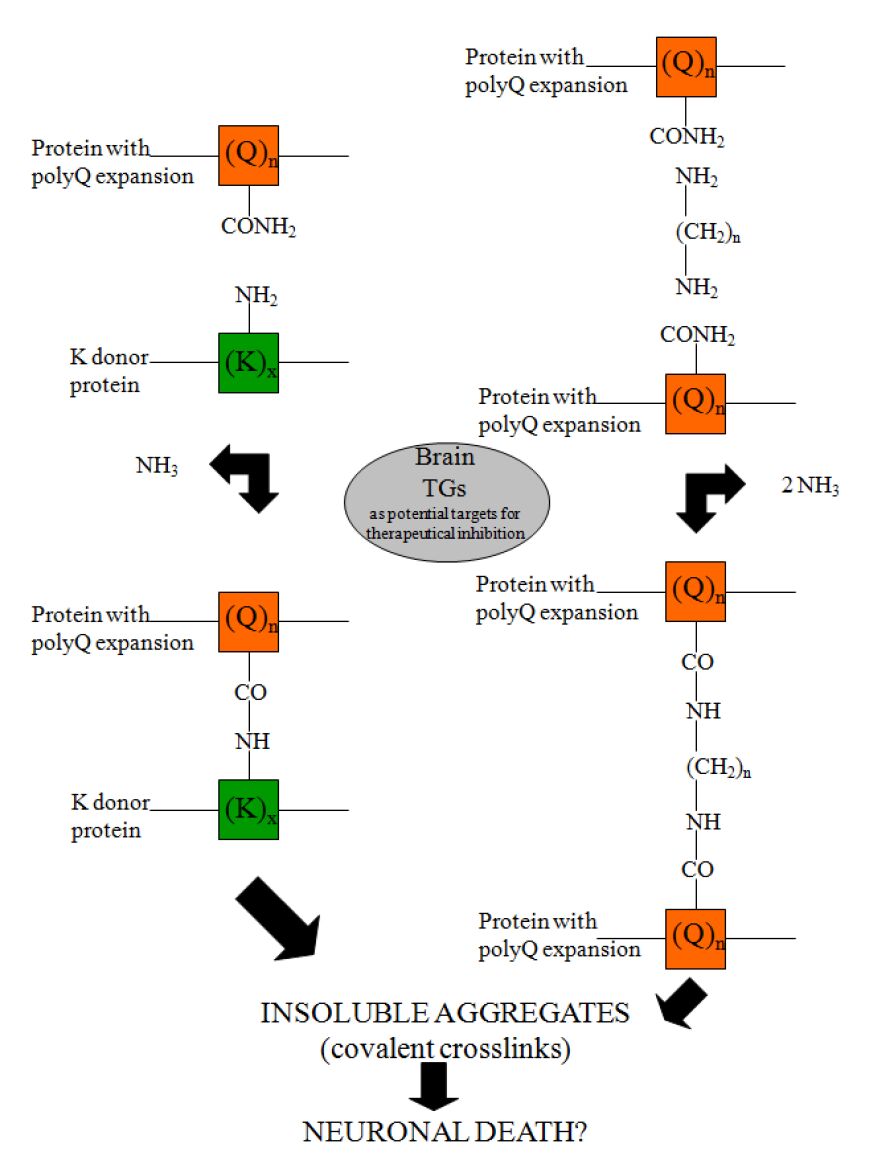
Although numerous scientific reports suggest that the transglutaminase activity is involved in the pathogenesis of neurodegenerative diseases, to date, however, persistently controversial experimental findings about the role of the TGs enzymes in these diseases have been obtained [29,30,31]. Protein aggregates in affected brain regions are histopathological hallmarks of many neurodegenerative diseases [32]. More than 20 years ago Selkoe et al. [33] suggested that TG activity might contribute to the formation of protein aggregates in AD brain. In support of this hypothesis, tau protein has been shown to be an excellent in vitro substrate of TGs [34,35] and GGEL cross-links have been found in the neurofibrillary tangles and paired helical filaments of AD brains [36]. Interestingly, a recent work showed the presence of bis γ-glutamyl putrescine in human CSF, which was increased in Huntington’s Disease (HD) CSF [37]. This is an important evidence that protein/peptides crosslinking by polyamines does indeed occur in brain, and that this is increased in HD brain. TG activity has been shown to induce also amyloid b-protein oligomerization [38] and aggregation at physiologic levels [39]. By these molecular mechanisms, TGs could contribute to AD symptoms and progression [39]. Moreover, there is evidence that TGs also contribute to the formation of proteinaceous deposits in Parkinson’s Disease (PD) [40,41], in supranuclear palsy [42,43] and in HD, a neurodegenerative disease caused by a CAG expansion in the affected gene [44]. For example, expanded polyglutamine domains have been reported to be substrates of TG2 [45,46,47] and therefore aberrant TG activity could contribute to CAG-expansion diseases, including HD (Figure 3). However, although all these studies suggest the possible involvement of the TGs in the formation of deposits of protein aggregates in neurodegenerative diseases, they do not indicate whether aberrant TG activity per se directly determines the disease progression. For example, several experimental findings reported that TG2 activity in vitro leads to the formation of soluble aggregates of α-synuclein [48] or polyQ proteins [49,50]. To date, as previously reported, at least ten human CAG-expansion diseases have been described (Table 2) [51,52,53,54,55,56,57,58,59,60] and in at least eight of them their neuropathology is caused by the expansion in the number of residues in the polyglutamine domain to a value beyond 35-40. Remarkably, the mutated proteins have no obvious similarities except for the expanded polyglutamine domain. In fact, in all cases except SCA 12, the mutation occurs in the coding region of the gene. However, in SCA12, the CAG triplet expansion occurs in the untranslated region at the 5' end of the PPP2R2B gene. It has been proposed that the toxicity results from overexpression of the brain specific regulatory subunit of protein phosphatase PP2A [57]. Most of the mutated proteins are widely expressed both within the brain and elsewhere in the body. A major challenge then is to understand why the brain is primarily affected and why different regions within the brain are affected in the different CAG-expansion diseases, i.e., what accounts for the neurotoxic gain of function of each protein and for a selective vulnerability of each cell type. Possibly, the selective vulnerability [61] may be explained in part by the susceptibility of the expanded polyglutamine domains in the various CAG-expansion diseases to act as cosubstrates for a brain TG (Figure 4). To strengthen the possible central role of the TGs in neurodegenerative diseases, a study by Hadjivassiliou et al. [62] showed that anti-TG2 IgA antibodies are present in the gut and brain of patients with gluten ataxia, a non-genetic sporadic cerebellar ataxia, but not in ataxia control patients. Recently, anti-TG2, -TG3 and -TG6 antibodies have been found in sera from CD patients, suggesting a possible involvement also of other TGs in the pathogenesis of dermatitis herpetiformis and gluten ataxia, two frequent extra intestinal manifestations of gluten sensitivity [63,64].
Table 2. List of polyglutamine (CAG-expansion) diseases.
| Disease |
Sites of neuropathology |
CAG triplet number |
Gene product (Intracellular localization of protein deposits) |
Reference |
| Normal |
Disease |
| Corea Major or Huntington’s Disease (HD) |
Striatum (medium spiny neurons) and cortex in late stage |
6-35 |
36-121 |
Huntingtin (n,c) |
[51] |
| Spinocerebellar Ataxia Type 1 (SCA1) |
Cerebellar cortex (Purkinje cells),dentate nucleus and brain stem |
6-39 |
40-81 |
Ataxin-1 (n,c) |
[52] |
| Spinocerebellar Ataxia Type 2 (SCA2) |
Cerebellum,pontine nuclei,substantia nigra |
15-29 |
35-64 |
Ataxin-2 (c) |
[53] |
| Spinocerebellar Ataxia Type 3 (SCA3) or Machado-Joseph disease (MJD) |
Substantia nigra,globus pallidus,pontine nucleus,cerebellar cortex |
13-42 |
61-84 |
Ataxin-3 ? |
[54] |
| Spinocerebellar Ataxia Type 6 (SCA6) |
Cerebellar and mild brainstem atrophy |
4-18 |
21-30 |
Calcium channel Subunit (a1A) (m) |
[55] |
| Spinocerebellar Ataxia Type 7 (SCA7) |
Photoreceptor and bipolar cells,cerebellar cortex,brainstem |
7-17 |
37-130 |
Ataxin-7 (n) |
[56] |
| Spinocerebellar Ataxia Type 12 (SCA12) |
Cortical,cerebellar atrophy |
7-32 |
41-78 |
Brain specific regulatory subunit of protein phosphatase PP2A (?) |
[57] |
| Spinocerebellar Ataxia Type 17 (SCA17) |
Gliosis and neuronal loss in the Purkinje cell layer |
29-42 |
46-63 |
TATA-binding protein (TBP) (n) |
[58] |
| Spinobulbar Muscular Atrophy (SBMA) or Kennedy Disease |
Motor neurons (anterior horn cells,bulbar neurons) and dorsal root ganglia |
11-34 |
40-62 |
Androgen receptor (n,c) |
[59] |
| Dentatorubral-pallidoluysian Atrophy (DRPLA) |
Globus pallidus,dentato-rubral and subthalamic nucleus |
7-35 |
49-88 |
Atrophin (n,c) |
[60] |
In support of the hypothesis of the toxic effect of TG activity in other neurodegenerative diseases, such as Alzheimer's disease and Parkinson's Disease, TG activity has been shown to induce amyloid beta-protein and a-synuclein oligomerization and aggregation at physiologic levels [65,66]. In fact, TG activity induces protofibril-like amyloid beta-protein assemblies that are protease-resistant and inhibit lonγ-term potentiation [39]. To support the role of the TGs also in Parkinson's disease, a recent work by Grosso et al. [67] has shown that TG2 exacerbates a-synuclein toxicity in mice and yeast. Therefore, by different molecular mechanisms, TG activity could contribute to Alzheimer's and Parkinson's diseases symptoms and progression. In addition, a recent work by Basso et al. [68] found that in addition to TG2, TG1 gene expression level is significantly induced following stroke in vivo or due to oxidative stress in vitro. Moreover, structurally diverse inhibitors, used at concentrations that inhibit TG1 and TG2 simultaneously, are neuroprotective. Together, these last studies suggested that multiple TG isoforms, not only TG2, participate in oxidative stress-induced cell death signalling, and that isoform nonselective inhibitors of TG will be most efficacious in combating oxidative death in neurological disorders. These are interesting and worthwhile studies, suggesting that multiple TG isoforms can participate in neuronal death processes. Therefore, all these studies suggest that the involvement of brain TGs could represent a common denominator in several neurological diseases, which can lead to the determination of pathophysiological consequences through different molecular mechanisms.
5. Transglutaminase Inhibition as Possible Therapeutical Approach
In consideration of the fact that up to now there have been no lonγ-term effective treatments for the human neurodegenerative diseases previously reported, the possibility that selective TG inhibitors may be of clinical benefit has been seriously considered. In this respect, some encouraging results have been obtained with TG inhibitors in preliminary studies with different biological models of CAG-expansion diseases. For example, cystamine (Figure 5) [69], is a potent in vitro inhibitor of enzymes that require an unmodified cysteine at the active site [70]. Inasmuch as TGs contain a crucial active-site cysteine, cystamine has the potential to inhibit these enzymes by a sulfide-disulfide interchange reaction. A sulfide-disulfide interchange reaction results in the formation of cysteamine and a cysteamine-cysteine mixed disulfide residue at the active site. Recent studies have shown that cystamine decreases the number of protein inclusions in transfected cells expressing the atrophin (DRPLA) protein containing a pathological-length polyglutamine domain [71]. In other studies, cystamine administration to HD-transgenic mice resulted in an increase in life expectancy and amelioration of neurological symptoms [72,73]. Neuronal inclusions were decreased in one of these studies [73]. Although all these scientific reports seem to support the hypothesis of a direct role of transglutaminase activity in the pathogenesis of the polyglutamine diseases, cystamine is also found to act in the HD-transgenic mice by mechanisms other than the inhibition of TGs, such as the inhibition of caspases [74], suggesting that this compound can have an additive effect in the therapy of HD. Currently, cysteamine is already in phase I studies in humans with HD [75], but several side effects, such as nausea, motor impairment and dosing schedule have been reported as reasons for non-adherence during phase II studies in human patients affected by cystinosis [76,77]. Another critical problem in the use of TG inhibitors in treating neurological diseases relates to the fact that, as previously reported, the human brain contains at least four TGs, including TG1, 2, 3 [23] and TG6 [78], and a strong non-selective inhibitor of TGs might also inhibit plasma Factor XIIIa, causing a bleeding disorder. Therefore, from a number of standpoints it would seem that a selective inhibitor, which discriminates between TGs, would be preferable to an indiscriminate TG inhibitor. In fact, although most of the TG activity in mouse brain, at least as assessed by an assay that measures the incorporation of radioactive putrescine (amine donor) into N, N-dimethyl casein (amine acceptor), seems to be due to TG2 [79], no conclusive data have been obtained by TG2 gene knock-out experiments about the involvement of this TG in the development of the symptoms in HD-transgenic mice [27,80,81]. Finally, while a recent scientific report showed that cystamine reduces aggregate formation in a mouse model of oculopharyngeal muscular dystrophy (OMPD), in which the TG2 knockdown is also capable of suppressing the aggregation and the toxicity of the mutant protein PABPN1 [82], suggesting this compound as a possible therapeutic for OMPD, vice versa, a more recent work reported that in a SCA3 gene knockdown drosophila model the inhibition of transglutaminase exacerbates polyglutamine-induced neurotoxicity by increasing the aggregation of mutant Ataxin-3[83].
6. Conclusions
In conclusion, numerous scientific reports have implicated aberrant TG activity in neurodegenerative diseases, but the need still exists for experimental findings that could definitely confirm the direct involvement of TGs in the pathogenetic mechanisms responsible for these diseases. However, as result of the putative role of specific TG isoforms, such as TG2, in some human diseases, there is a considerable interest in developing inhibitors of these enzymes. Of those currently available, cystamine is the most commonly used experimentally to inhibit TG2 activity. In addition to cystamine, several types of TG2 inhibitors have been developed up to now [84,85]. Interestingly, some of these inhibitors have shown promising results in experimental diabetic models [86]. Therefore, the use of these inhibitors of TGs could be then useful also for other clinical approaches. To minimize the possible side effects, however, more selective inhibitors of the TGs should be required in the future. Progress in this area of research could be achieved also through pharmaco-genetic techniques.
Acknowledgements
This work is supported by the Italian Education Department and the Regione Campania (L.R. n.5 del 28.03.2002, finanziamento 2008).
Conflict of Interest
Authors do not have any conflict of interest.









 DownLoad:
DownLoad: