New convergence on inertial neural networks with time-varying delays and continuously distributed delays

1.   Introduction

Inertial neural networks system is a class of second order delay differential equations proposed by Babcock and Westervelt ^[1]. It is established by introducing an inertia term into the multi-directional associative memory neural networks, and is widely used in the fields of optimization, associative memory, image processing, psychophysics, and adaptive pattern recognition ^[1]. Therefore, it is of great significance to study the dynamic behaviors (such as stability ^[2,3,4,5,6], dissipation ^[7,8,9], Hopf bifurcation ^[10,11,12], Lagrange stability ^[13,14,15], synchronization ^{[16,17,18,19,20]}, etc.) of the system in the application of inertial neural networks. It is worth noting that the dynamics analysis on inertial neural networks is usually to convert them into a first-order differential system by reducing order variable substitution under the assumption that the activation functions are bounded ^{[21,22,23,24]}. In particular, the periodicity, stability and convergence for the inertial neural networks systems have been established in ^{[25,26,27,28,29,30]} by using the reduced order method. However, this method needs to introduce some new parameters, which will raise the dimension in the inertial neural networks system. This will increase huge amounts of computation and it is difficult to achieve in practice ^[3,4,20]. Therefore, the authors of ^[3,4,20] have developed some non-reduced order methods to establish the stability and synchronization conditions of inertial neural networks with constant or time-varying delays, respectively.

Because there are many parallel paths with a series of different axon sizes and lengths in the neural networks, it is necessary to introduce continuous distributed delays to describe the transmission of neuron signals. In recent years, a large number of literatures have studied the dynamic behaviors of inertial neural networks with unbounded distributed delays ^{[31,32,33,34,35,36,37]}. In particular, the author of literature ^[36] studied the global convergence of inertial neural networks with continuous distributed delays by using a non-reduced order method:

and

where $BC((-\infty, 0], \mathbb{R})$ is the set of all continuous and bounded functions from $(-\infty, 0]$ to $\mathbb{R}$, $x(t) = (x_1(t), \ x_2(t), \cdots, x_n(t))$ is the state vector, $x''(t)$ is called an inertial term of (1.1), the time-varying connection weights $c_{ij}, \ h_{ij} : \mathbb{R} \rightarrow \mathbb{R}$ and $a_i, \ b_i : \mathbb{R} \rightarrow (0, +\infty)$ are bounded and continuous functions, the delay kernel $K_{ij}: [0, \ +\infty)\rightarrow \mathbb{R}$ is a continuous function, the external input $J_i(t)$ and the activation function $\tilde{P}_j$ and $\tilde{R}_j$ are continuous, and $i, \ j\in S$.

Unfortunately, in the initial values (1.2) which also adopted in ^[24,35], the assumption that

is incorrect. In fact, in the system (1.1), the transmission term $a_i(t)x'_i (t)$ is not affected by the delays. Combined with the theory of the delay differential equation, we can see that in the initial problem (1.2), it is not necessary to assume that $x'_i (t)$ is bounded and continuous on $(-\infty, \ 0]$, which leaves room for further improvement.

On the other hand, the dynamic characteristics of the inertial neural networks are usually affected by time-varying delays and distributed delays. Therefore, it is especially significant to study the following inertial neural networks system with bounded time-varying delays and unbounded continuously distributed delays:

where $J_{i}, c_{ij}, d_{ij}, h_{ij} :\mathbb{R}\rightarrow \mathbb{R}$, $a_{i}, \ b_{i} :\mathbb{R}\rightarrow (0, +\infty)$ and $\tau_{ij}:\mathbb{R}\rightarrow \mathbb{R}^+$ are bounded and continuous functions, the delay kernel $K_{ij} \in C([0, +\infty), \mathbb{R})$ is a continuous function, the activation functions $\tilde{P}_i, \ \tilde{Q}_i, \ \tilde{R}_i$ are continuous, and $i, j \in S$.

As is well known that the Lyapunov function structure of unbounded time-delay systems is more complex than bounded time-delay systems, therefore, the stability of the former is more difficult to establish than the latter. Especially, there are few studies on the dynamic behaviors of inertial neural networks with bounded time-varying delays and unbounded distributed delays. So far, we only find that the authors of ^[38] have discussed the existence and exponential stability of the periodic solution of system (1.3) with periodic input functions. However, to the best of our knowledge, there has not yet been research work on the global convergence analysis for the system (1.3) by utilizing a non-reduce method.

Regarding the above discussions, in this manuscript, the initial value (1.2) is modified to

and the global convergence criterion of the inertial neural networks (1.3) is established by applying a non-reduce method. In a nutshell, the contributions of this paper can be summarized as follows. 1) Without adopting the periodicity on the input functions, a class of inertial neural networks with bounded time-varying delays and unbounded continuously distributed delays are proposed; 2) Under some appropriate assumptions, a non-reduce approach is developed to show that all solutions and their derivatives in the proposed model are convergent to the zero vector; 3) The initial value conditions (1.2) in ^[24,35,36] are relaxed into a broader situation; 4) Numerical results including comparisons are presented to verify the obtained theoretical results.

The structure of this paper is as follows. The global convergence of the solutions and their derivatives of system (1.3) is established in section 2. Then, section 3 presents a concrete example with the numeric simulations to show the feasibility of the main results. Section 4 contains a conclusion of this paper and the further research of the topic.

2.   Global convergence of system (1.3)

In this section, we use the following Barbarat's lemma to prove the global convergence of the system (1.3).

Lemma 2.1 ^[36] If $g(t)$ is uniformly continuous on interval $[0, \ +\infty)$, and $\int_0^{+\infty} g(s)ds$ exists and is bounded, then $\lim\limits_{t\rightarrow +\infty}g(t) = 0$.

Assumptions:

$(G_{1})$ there exist three constants $L^{P}_{j}$, $L^{Q}_{j}$ and $L^{R}_{j}$ such that

$(G_{2})$ for $i, j \in S$, $|K_{ij}(t)|$ is integrable on $[0, +\infty)$.

$(G_{3})$ $u(t) = \max\limits_{i\in S}|J_i(t)|, \ U(t) = \int_0^t u(s)ds$ is bounded on $[0, +\infty)$.

$(G_{4})$ for $i, j \in S$, $a'_i(t), \ b'_i(t)$ and $(|c_{ij}(t)|L^{P}_{j} +|d_{ij}(t)|L^{Q}_{j} + |h_{ij}(t)|L^{R} _{j}\int_{0}^{+\infty}| K_{ij}(u)| du)'$ are bounded and continuous on $[0, +\infty)$.

$(G_{5})$ there exist constants $\beta_{i} > 0$ and $\alpha_{i}\geq 0, \gamma_{i}\geq 0$ satisfying

where

$(G_{6})$ for $i, \ j\in S$, $\tau_{ij}$ is continuously differentiable, and $\tau_{ij}'(t) = \dot{\tau}_{ij} < 1$ for all $t\in \mathbb{R}$.

Remark 2.1. Combining $(G_{1})$, $(G_{2})$ and the basic theory on functional differential equation with infinite delay in ^[40], one can show that all solutions of the initial value problem $(1.3)$ and (1.4) exist on $[0, \ +\infty).$

Remark 2.2. In this paper, $(G_{3})$ means that the input functions are absolutely integrable on $[0, \ +\infty),$ and $(G_{4})$, which is related the delay kernels, implies the specific effect of time delay functions on the convergence of system (1.3).

Theorem 2.1 Assume that $(G_{1})$–$(G_{6})$ hold. Let $x(t) = (x_{1}(t), x_{2}(t), \cdots, x_{n}(t))$ be a solution of the initial value problem (1.3) and (1.4). Then $\lim\limits_{t\rightarrow+\infty}x_{i}(t) = 0, \ \ \lim\limits_{t\rightarrow+\infty}x'_{i}(t) = 0.$

Proof. According to $(G_{3})$, $(G_{5})$ and the boundedness of coefficients in (1.3), one can choose two positive constants $\rho$ and $\varrho$ such that

Let

It follows from $(G_{2})$, $(G_{3})$, $(G_{6})$ and (1.3) that

The assumption $(G_{1})$ and the fact that $uv \leq \frac{1}{2}(u^{2} + v^{2}) (u, v\in \mathbb{R})$ entail that

and

which, together with $(G_4)$, (2.2) and (2.3), give

This implies that $W(t)\leq W(0)$ for all $t \in [0, +\infty)$, and

Since $\alpha_{i} | x'_{i}(t)|\leq |\alpha_{i}x'_{i}(t)+\gamma_{i}x_{i}(t)|+|\gamma_{i}x_{i}(t)|,$ it follows that $x'_{i}(t)$ and $x_{i}(t)$ are uniformly bounded on $[0, \ +\infty)$ for all $i\in S$. According to the continuity of right-hand side functions in (1.3), it is easy to see that $x''_{i}(t)$ is also uniformly bounded on $[0, \ +\infty)$ for all $i\in S$, which combining with $(G_4)$ lead that $\sum\limits_{i = 1}^{n}\Big(x'_{i}(t)+\frac{F_{i}(t)}{2D_{i}(t)}x_{i}(t)\Big)^{2}$ and $\sum\limits_{i = 1}^{n}x_{i}^{2}(t)$ are uniformly continuous on $[0, \ +\infty)$.

In addition, (2.4) entails that

and

which, together with Lemma 2.1, lead to

The proof is complete.

Remark 2.3. Obviously, system (1.1) is a special case of system (1.3) when $d_{ij} = 0, \ i, j\in S$, and the restrictions on initial value condition (1.4) are weaker than those ones in (1.2), hence all the results in ^[30] can be derived from theorem 2.1. Moreover, the global Lipschitz conditions on the activation functions were crucial in ^[3,20,31] where the convergence on the state vector of inertial neural networks system was considered. However, in this paper, the global Lipschitz conditions have been abandoned and the global convergence on the inertial neural networks system with bounded time-varying delays and unbounded continuously distributed delays has been established. This implies that Theorem 2.1 generalizes and complements the main results of ^[3,20,30,31].

3.   A numerical example

Example 3.1. Regard the following inertial neural networks with mixed delays:

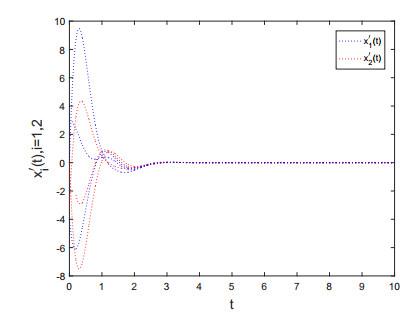
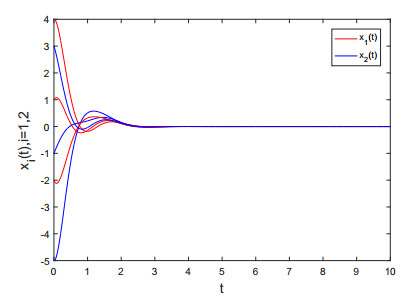
where $\tilde{P}_{1}(u) = \tilde{Q}_{1}(u) = \tilde{ R}_{1}(u) = 0.25(|u + 1|-|u-1|), \ \tilde{P}_{2}(u) = \tilde{Q}_{2}(u) = \tilde{ R}_{2}(u) = 0.5 u (\sin^3 u).$ Take $\alpha_{i} = \gamma_{i} = 1, \ \beta_{1} = 18.14, \ \beta_{2} = 19.16, \ L^{P}_{i} = L^{Q}_{i} = L^{K}_{i} = 0.5, \ i = 1, 2,$ we gain $D_{i} (t) < 0, \ \ \ 4D_{i} (t) E_{i } (t) > (F_{i} (t))^{2}, \ i = 1, 2, \ t\in \mathbb{R}.$ By Theorem 2.1, we can conclude that all solutions of (3.1) and the derivatives are convergent to the zero vector, respectively. Simulations in Figures 1 and 2 reflect that the theoretical convergence is in sympathy with the numerically observed behavior. Here, it can be seen from the moving trend of the trajectories in Figures 1, 2 that $x_{i}(t)$ and $x_{i}'(t)$ are convergent to $0$ as $t\rightarrow +\infty$.

Remark 3.1. It should be pointed out that $\tilde{P}_{2}(u) = \tilde{Q}_{2}(u) = \tilde{ R}_{2}(u) = 0.5 u (\sin^3 u)$ does not satisfy the global Lipschitz condition, and $d_{11}, \ d_{12}, \ d_{21}, d_{22}\neq 0$, then all results in the references ^{[24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70]} can not be straightly applied to show that every solution and its derivative convergent to the zero vector in system (3.1). Moreover, as far as the authors know, the convergence on inertial neural networks with bounded time-varying delays and unbounded continuously distributed delays without applying the reduced-order method has not been touched in the previous literature. Consequently, the main results established in this paper are essentially new and complement some existing ones.

4.   Conclusions

In this paper, applying differential inequality techniques coupled with Lyapunov function method instead of the reduced order method, we study the global convergence on inertial neural networks with bounded time-varying delays and unbounded continuously distributed delays. Some sufficient assertions have been established to guarantee that every solution and its derivative of the addressed model are convergent to the zero vector. It should be mentioned that the method applied in this paper provides a possible approach to study the topic on dynamical behaviours of other inertial neural networks model with bounded time-varying delays and unbounded continuously distributed delays.

Acknowledgments

The authors would like to express the sincere appreciation to the editor and reviewers for their helpful comments in improving the presentation and quality of the paper. This work was supported by the Postgraduate Scientific Research Innovation Project of Hunan Province (No. CX20200892).

Conflict of interest

We confirm that we have no conflict of interest.