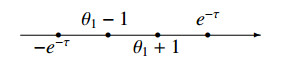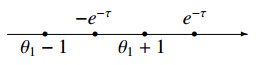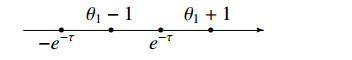For two continual bases in the representation space, we obtain the matrix elements of the linear operator transforming the first basis into the second. These elements are expressed in terms of Coulomb wave functions. Computing the matrix elements of subrepresentations to some subgroups or their separate elements and using the connection between above bases, we evaluate some integrals involving Coulomb wave functions.
1.
Introduction and preliminaries
The Coulomb wave functions Fσ(ρ,λ) and H±σ(ρ,λ) are functions belonging to the kernel of the Coulomb differential operator (see, e.g., [18,Chapter 33])
where λ∈R+, ρ∈R (Sommerfeld parameter), and σ∈N0 (angular momentum quantum number). Here and throughout, we denote C, R, R+, Z, and N by the sets of complex numbers, real numbers, positive real numbers, integers, and positive integers, respectively, and let N0:=N∪{0}, Z−0:=Z∖N. The functions Fσ(ρ,λ) and H±σ(ρ,λ) satisfy the following formulas (see [6]):
and
where i=√−1, Mμ,ν(z) and Wμ,ν(z) are Whittaker functions of the first kind and the second kind (see, e.g., [1,Sections 4.3 and 4.4]), respectively, and the normalizing constant (Gamow factor) Nσ(ρ) and Coulomb phase shift nσ(ρ) are given as follows:
and
where Γ is the familiar Gamma function (see, e.g., [27,Section 1.1]). The functions Fσ(ρ,λ) and H±σ(ρ,λ) may also be continued analytically to λ∈C∖{0}, and ρ,σ∈C (see, e.g., [5,8]; see also [18,Entry 33.13]).
Recall the generalized hypergeometric series pFq (p,q∈N0) defined by (see, e.g., [22,p. 73]):
where (λ)ν denotes the Pochhammer symbol which is defined (for λ,ν∈C), in terms of the familiar Gamma function Γ, by
it being understood conventionally that (0)0:=1.
Since the two Whittaker functions are determined by the confluent hypergeometric function 1F1 (see, e.g., [7,Entries 6.5(7),6.9(1) and 6.9(2)]) which satisfies the following Kummer's transformation formula (e.g., [7,Entry 6.3(7)])
the choice of ambiguous signs in (1.1) and (1.2) is immaterial, provided that either all upper signs are taken or all lower signs are taken (see, e.g., the comment after [18,Entry 33.2.5]).
Also recall (see, e.g., [18,Entry 33.2(ⅲ)])) that H+σ(ρ,λ) and H−σ(ρ,λ) are complex conjugates, and their real and imaginary parts are given by
Here Fσ(ρ,λ) is the regular solution of the Coulomb wave equation d[y]=0 while Gσ(ρ,λ) and H±σ(ρ,λ) are its irregular solutions.
Since the dimension of the space Kerd is 2, the linearly independent functions Fσ(ρ,λ) and Gσ(ρ,λ) form a basis in Kerd. Another basis consists of H+σ(ρ,λ) and H−σ(ρ,λ). Curtis [4] considered two other bases in Kerd consisting of functions which are still named Coulomb functions (see also [11,14]).
Recall another differential operator (see [12]):
The so-called Bessel-Clifford function of the first kind
is one of the functions belonging to Kerb. The function Cσ(λ) in (1) is related to the Bessel function Jσ as follows:
Likewise the modified Bessel-Clifford function of the second kind Kσ(λ) can be expressed via the Macdonald function Kσ:
We also need the following integral transformations:
The first Hankel-Clifford integral transform (see [16,Eq. (2.7)])
The second Hankel-Clifford integral transform (see [13]; see also [16,Eq. (2.9)])
The Macdonald-Clifford transform
In this paper, we aim to present new formulas which involve Coulomb functions and are related to a representation of the three-dimensional proper Lorentz group in one appropriate carrier functional space (called here the representation space). The paper is organized as follows: In Section 2 we describe the representation space and two bases in it. In Section 3 we express the connection between above bases in terms of Coulomb functions (basically, in terms of Fσ(ρ,λ)). In Sections 4–8 we consider some restrictions of our representation to some subetaoups or their separate elements and, using the connections between bases, obtain some integral formulas. In particular, for diag(−1,1,−1) and the (circle) rotations through π and π2 in the plane Ox2x3 we obtain the Bessel–Clifford and Mellin transforms or Coulomb functions, respectively, which are expressed in terms of Coulomb functions and Gaussian hypergeometric functions. Considering the product of the maximal nilpotent subetaoup and the subetaoup of hyperbolic rotations in the plane Ox1x2, we express one integral involving product of Coulomb functions in terms of Appell hypergeometric function.
The same problem for two different pairs of bases in the similar representation space for the four-dimensional analogue of our group has been considered in the papers [25] and [26], in which the related theorems have been formulated in terms of 4F3 and Macdonald functions, respectively.
2.
Representation space, its bases, and functionals F1 and F2
We recall that the three-dimensional Lorentz group is the subetaoup of matrices (gij) in GL(3,R) satisfying the equalities
where E(μ) denotes the integer part of μ∈R, and gi1gj1−gi2gj2−gi3gj3=0 for different i,j∈{1,2,3}. In this paper, we consider the intersection G of this group with SL(3,R), calling G the proper Lorentz group. Let σ∈R and T be the representation of G in the linear space D consisting of σ-homogeneous and infinitely differentiable functions defined on the cone
acting according to rule T(g)[f(x)]=f(g−1x) (see [30]). The similar realization of the G-representation can be considered on hyperboloid x21−x22−x23=r2 (see [32]).
We recall that the functions xμ± on R, which generate the generalized functions (xμ±,f), are defined as follows (see [9]): For μ∈C, xμ± is equal to |x|μ for x∈R+ and coincides with zero function otherwise. Here we deal with the bases (see [31])
and
In the following, we use two bilinear functionals defined on pairs of representation spaces in the same way as in [24]. In order to introduce them, we define the following subsets on Λ: parabola γ1:x1+x2=1 and hyperbola γ2=γ2,+∪γ2,−, where γ2,±:x2=±1. Let Hi be a subetaoup of G, which acts transitively on γi. We define F1 and F2 as
where dγi is a Hi-invariant measure on γi. Let γ1 and γ2,± be parameterized as follows:
where α1,α2∈R. Since the subetaoups H1 and H2 consist of matrices, respectively,
and
where θ1,θ2∈R, and
we have dγi=dαi. Also these identities mean that fλ is an eigenfunction of the operator T(h1(θ1)) and fρ,± is an eigenfunction of T(h2(θ2)) with eigenvalues exp(−θ1λ) and exp(−θ2ρ), respectively. It was shown in [24] that F1 and F2 coincide on pairs (D,D∙) such that degree of homogeneity of D∙ is equal to −σ−1.
3.
Matrix elements of B1⇄B2 and B∙1⇄B∙2 transformations in terms of Coulomb functions
Express a function fλ∈B∙1 as a linear combination of vectors belonging to B∙2:
Since
we have
where δ(ρ+ˆρ) is the ˆρ-delayed Dirac delta function. Therefore,
Likewise, if
then
Considering that σ is the third argument (after ρ and λ) of c∙ρ,±,λ, we derive from (3.4) that
Theorem 3.1. The c∙λ,ρ,+ in (3.3) is expressed in terms of the Coulomb wave function in (1.1) as follows:
Proof. Recall a known formula (see, e.g., [10,Entry 3.383-1] and [19,Entry 2.3.6-1])
where B(α,β) is the familiar Beta function given by (see, e.g., [27,Section 1.1])
Then
where (3.7) is applied for the fifth equality. For the 1F1 of the last expression, using the following known relation (see, e.g., [1,Eq. (4.3.2)], [17,p. 290])):
we find
which, in view of (3.8), is equivalent to
Since Γ(z) is analytic in the half plane ℜ(z)>0 whose domain is symmetric with respect to the real axis x=ℜ(z)∈R+ and Γ(x)∈R on the real axis x=ℜ(z)∈R+, by reflection principle (see, e.g., [3,p. 57]), we have Γ(ˉz)=¯Γ(z) for each z in the half plane ℜ(z)>0. Therefore (3.10) is rewritten as follows:
From (1.1) and (1.3),
Finally, using (3.12) in (3.11), we obtain the desired result (3.6).
Theorem 3.2. Let −1<σ<0 and λ≠0. Then
Or, equivalently,
Proof. We have
Recalling an integral formula (see, e.g., [19,Entry 2.3.2.(3)])
and using (3.9) and (1.1), we obtain
where
(see also [10,Entry 9.220.(4)]). Using (1.2), we derive (3.13). Using (3.13) and (1.4), we obtain (3.14).
4.
Formulae related to the matrix diag(−1,1,−1)
For any f∙λ and any g∈G, let us express T∙(g)[f∙λ] as the integral operator
where t∙λˆλ are the matrix elements of the representation T∙. Then
Choosing here i=1, in view of
where δ(ˆλ+˜λ) is the (−˜λ)-delayed Dirac delta function, we have
Thus
From (3.1) and (4.1), for any g∈G, we have
where
On the other hand,
Since f∙ρ,+ is an eigenfunction of the linear operator T∙(diag(−1,1,−1)) with eigenvalue (−1)iρ, we have
We express the matrix elements tλˆλ(diag(−1,1,−1)) in terms of Bessel-Clifford functions as in the following theorem.
Theorem 4.1. Let −1<σ<0. Then
and
Proof. Since
and
we find from (4.2) that
Using known integral formulas (see [19,Entry 2.5.24.4]), we obtain the following integral formulas: For ab>0 and |ℜ(α)|<1,
and
Using (4.7) and (4.8) to evaluate the integral (4.6), with the aid of the relations (1.5) and (1.6), we derive the expressions (4.4) and (4.5).
Using (4.3) and Theorems 3.1 and 3.2, we obtain the following identity
The identity (4.9) can be rewritten in the following theorem.
Theorem 4.2. Let λ>0 and −1<σ<0. Then
Considering the case λ<0 in (4.3), we obtain the following similar result.
Theorem 4.3. Let λ<0 and −1<σ<0. Then
5.
Formulae related to the rotation through π in the plane Ox2x3
Let Un be the multiplicative group of all complex roots of the equation zn=1 (n∈N). Then, for any ε∈U2, we have diag(1,ε,ε)∈G and
Therefore,
The trivial case ε=1 gives tλˆλ(id)=δ(λ−ˆλ). The case ε=−1 yields the following theorem.
Theorem 5.1. Let λ>0 and −1<σ<0. Then
Proof. The proof of (5.1) would run parallel to that of Theorems 4.1 and 4.2. We omit the details.
Another result corresponding to (5.1) for the case λ<0 is left to the interested reader.
6.
One formula related to the rotation through π2 in the plane Ox2x3
In this section we use the subetaoup H∘ consisting of (circle) rotations
Note that the subetaoup H∘ is isomorphic to the group SO(2).
For any g∈G, let us express the function T∙(g)[f∙ρ,±] as linear combinations of functions belonging to the basis B∙2:
The equation (6.1) gives that, for any k∈Z,
Choosing here j=1 and considering (3.2), we have
Therefore,
Or, equivalently,
Theorem 6.1. Let −1<σ<0. Then
Proof. We find
Using a known integral formula (see [19,Entry 2.2.6.(1)])
we obtain
We also find
where
Thus, t∙ρ,+,ˆρ,+(h∘(π2)) can be expressed in terms of Gamma functions (see, e.g., [19,Entry 2.3.4(1)]). Now, the statement of the theorem follows from (3.5), (6.2), and (6.4).
Remark 1. From Theorem 4.2 and throughout, F−σ−1(−ρ,−λ) can be changed by the linear combination of basis functions in Kerd (see [5])
where
7.
Formulae related to the hyperbolic rotations in the plane Ox1x2
In this section we deal with the subetaoup H∗ of matrices
in G.
Theorem 7.1. Let −1<σ<0 and τ>0. Then
where Qμν(x) is the associated Legendre function of the second kind.
Proof. Computing the matrix elements of the subrepresentation T∙ to H∗, we obtain
Since coshτcoshα2+sinhα2+sinhτ>0 and σ+1>0, using a known integral formula (see [19,Entry 2.5.48.(6)])
we have
Also,
Here
where the last integral is evaluated by using (3.7). Therefore we have
Finally, considering (7.1) and (7.2), we complete the proof.
Remark 2. Cylindrical (ordinary) and spherical Bessel functions can be expressed in terms of Coulomb function, respectively, by the following formulas (see, e.g., [29,Eqs. (2.1a) and (2.1c)]
8.
Formulae related to the product of subgroups H1 and H∗
In this section we show that the matrix elements of the subrepresentation T∙ to the subetaoup H1H∗ yield four integral representations of the Appell function F1, which depend on the relations between parameters θ1 and τ and correspond to Figures 1–4.
Theorem 8.1. Let −1<σ<0 and e−τ<|θ1±1|. Then
Proof. We show that both functionals F1 and F2 are invariant with respect to the pair (T∙(h∗),T(h∗)) of representation operators. Indeed, in view of homogeneity of u and v,
Since T∙ is a homomorphism (of G to the group GL(D∙) of linear operators of D∙ with trivial kernels) and H1 is an one-parameter subetaoup (that is, h−11(θ1)=h1(−θ1)), we have
where Ω is the intersection of the segments |α1|≤e−τ and [θ1−1,θ1+1]. Under the assumption e−τ<|θ1±1| (Figure 1), this integral can be evaluated by using a known integral formula (see [10,Entry 3.211]): For min{ℜ(μ),ℜ(ν)}>0,
Also,
We thus have
Using (1.1), (3.7) and (3.9), we get
Using (3.5), we have
Considering (8.1) and (8.2), we complete the proof.
Employing the same proof as in Theorem 8.1 for the cases corresponding to Figures 2–4, we obtain the following results, without their proofs, which are given in Theorems 8.2, 8.3 and 8.4.
Theorem 8.2. Let r -1 < \sigma < 0 and |\theta_1\pm1| < e^{-\tau} . Then
Theorem 8.3. Let -1 < \sigma < 0 , \big|\theta_1+e^{-\tau}\big| < 1 , and |\theta_1+1| < e^{-\tau} . Then
Theorem 8.4. Let -1 < \sigma < 0 , \big|e^{-\tau}-\theta_1\big| < 1 , and |\theta_1-1| < e^{-\tau} . Then
Remark 3. In Theorems 8.1–8.4, the Appell function F_1 can be rewritten in terms of the hypergeometric function {}_2F_1 by using the following relation (see, e.g., [21,Entry 7.2.4.(63)])
9.
Concluding remarks
The group theoretic approach gives a natural (in some sense) technique to obtain formulas for integral transforms of special functions, since they occur in relations between kernels of integral operators of representations calculated in different ordinary and mixed bases and matrix elements of basis transformations. For instance, by evaluating the Mellin-Laplace transform of the Coulomb Sturmian radial function, Morales [15] used series decomposition and integration term-by-term to show that the integral
is equal up to multiplicative constant to
where l, j\in\mathbb{N}_0 and \omega > -1 . For investigation of matrix elements of two-body Coulomb interaction in the lowest Landau level, Bentalha [2,Lemma 1] obtained the following integral formula for product of associated Laguerre polynomials (l, m, n\in\mathbb{N}_0) expressed in terms of Appell F_2 function:
which may be also expressed in terms of {}_3F_2 (see, e.g., [20,Entry 2.19.14.(9)] and [28]). Since L_n^{2l+1}(x) up to multiplicative constant coincides with {}_1F_1(-n; 2l+2;x) , we have in (9.1) and (9.2) Mellin-Laplace integrals for Whittaker functions of the first kind, which are related to regular Coulomb function F_\sigma(\rho, \lambda) . The results in Theorems 8.1–8.4 are concerned with the Mellin-Fourier transform for Coulomb functions and, in this regard, are closely related to the examples (9.1) and (9.2). It may be said that, in some sense, Theorems 8.1–8.4 are complexifications of these examples.
Theorems 4.1–8.4 are based on the fact (described in Theorems 3.1 and 3.2) that the matrix elements c_{\rho, \pm, \lambda} and c_{\lambda, \rho, \pm} (kernels of corresponding integral operators) of the transformations B_1\longrightarrow B_2 and B_2\longrightarrow B_1 can be expressed in terms of Coulomb wave function F_\sigma(\rho, \lambda) . In all these theorems (except Theorem 5.1), we have used only integrals of the following forms
Analogous integral transforms to those in this paper, containing kernels c_{\rho, -, \lambda} and c_{\lambda, \rho, -} , can yield similar results. Also these kernels were considered for two dual cases \sigma = -\frac12\pm\frac14 in [23].
Acknowledgments
The authors are grateful to the anonymous referees for the constructive and valuable comments which improved this paper.
Conflict of interest
The authors declare that they have no conflict of interest.
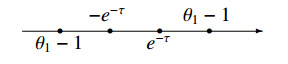









 DownLoad:
DownLoad: