1. Introduction

Energy use in global urban areas is responsible for 69% of anthropogenic GHG emissions, 90% of which is CO₂ ^[1]. The global and US national average proportions of on-road emissions are 24 and 27% of the total FFCO₂ emissions ^[1] but in California, it is 43% of the total ^[2]. Because of the importance of on-road FFCO₂ emissions, particularly within urban domains, sub-national climate change policy must include means to reduce emissions from this sector.

The most comprehensive policies and strategies for mitigation of FFCO₂ emissions in the US transportation sector are being implemented in California ^[3,4]. These aim to reduce fossil fuel use, diversify the fuel mix, and reduce vehicle kilometers traveled ^[5]. For instance, Senate Bill 375, focusing solely on light-duty vehicle emissions, specifically targets GHG emission reductions from passenger vehicles that account for 78% of California's GHG emissions from the transportation sector ^[3]. The Southern California Association of Governments (SCAG) has designed the 2012–2035 Regional Transport Plan/ Sustainable Communities Strategy (RTP/SCS) to achieve the state's GHG reduction goals and address the requirements of SB 375. At the local level, the City of Los Angeles and other cities in the larger LA megacity are moving towards reduction of FFCO₂ emissions. However, in order to predict future emissions accurately and analyze different mitigation options in a more targeted fashion, reliable urban fossil fuel carbon dioxide (FFCO₂) emission inventories ^[6], with explicit spatio-temporal and functional detail (e.g. road type, vehicle type), are needed ^[7,8,9]. Such information would offer the opportunity to target particular locations of travel modes, difficult to achieve with the limited information cities have at their disposal now.

A number of approaches have been used to quantify on-road FFCO₂ emissions and can be employed to generate high-resolution emissions. For example, travel demand models that characterize different travel activities have been integrated with emissions factors or meteorological data to model on-road traffic emissions ^[10,11]. These activity-based models are based on predicted travel behavior and hence, cannot account for sudden changes in travel behavior. Our approach (Hestia Project version 1.0), on the other hand, takes into account the actual traffic volume observed. Researchers have also used an approach that is driven from fuel sales, as a proxy for vehicle activity, to estimate FFCO₂ emissions ^[12,13]. However, this approach can lead to space and time inaccuracies because the points of fuel sales are typically not co-located with vehicle travel.

An alternative to these approaches is to use estimates of vehicle activity (vehicle kilometers traveled–VKT) combined with fleet composition and vehicle fuel efficiency to estimate FFCO₂ emissions. This approach is particularly well-suited to estimating space/time-explicit, functionally-detailed estimates of on-road FFCO₂ emissions as traffic monitoring (at the core of both the activity and temporal distribution) can be tied to individual road segments. The advantage of this approach is the emphasis on vehicle combustion in space and time. However, it does not contain information related to the purpose, origin, or destination of travel.

In this paper, we describe the on-road FFCO₂ emissions estimates in the Los Angeles Megacity domain developed as part of the Hestia Project version 1.0. This project has generated high-resolution FFCO₂ emissions estimates of all fossil combustion sources within whole urban domains down to the scale of individual buildings and roadways. Begun roughly 8 years ago, Hestia estimates have been generated for Indianapolis, Salt Lake City, the Los Angeles Basin, and Baltimore. By quantifying emissions down to individual buildings and road segments, the Hestia Project provides spatial, temporal, and mechanistic (building type, vehicle type, fuel, etc.) detail for an entire city. The Hestia effort was initially begun to complement urban emissions estimation using atmospheric CO₂ inversion approaches ^[14], but is also valuable as a detailed inventory of emissions offering city decision makers guidance to optimize GHG emission mitigation.

Our aim is to report on hourly estimates of FFCO₂ emissions for each road segment in the LA megacity, deconstructing characteristics of the on-road emissions and highlighting emission hotspots. In section 2 we provide a description of the methods used to estimate on-road FFCO₂ emissions and the statistical techniques to analyze the results. In section 3 we report on our results, analyzing both the spatial and temporal patterns and emission hotspots. We also provide uncertainty estimates and a comparison to two other available data products derived from different approaches. Finally, in section 4 we discuss the implications of these results for the development of abatement technologies and policies, and the mitigation of FFCO₂ emissions.

2. Materials and Methods

Our study area is the Los Angeles megacity within the South Coast Air Basin. The megacity comprises 153 cities, has a population of around 16.3 million people (~42% of California's population) ^[15], and a geographical area of 17,100 km². It includes all of Orange county, most of Los Angeles county and the urbanized portions of Riverside and San Bernardino counties. The Los Angeles megacity consists of two major metropolitan areas, Los Angeles-Long Beach-Anaheim and Riverside-San Bernardino-Ontario, and therefore, is California's largest metropolitan region ^[16].

The LA megacity contributes to ~43% (41.5 million tC) of California's FFCO₂ emissions ^[2,17]. On-road transportation is the largest FFCO₂ emissions sector in the LA megacity, constituting around 49% (19 million tC yr^-1) of the total. The topography of the basin, with mountains in the north and east and Pacific ocean in the south and west, contributes to its persistent elevated pollution levels.

2.1. Annual on-road FFCO₂ emissions

Annual 2012 on-road FFCO₂ emissions for the LA megacity were derived from the EMFAC2011 transportation emissions model ^[18] developed by the California Air Resources Board (CARB). EMFAC2011 uses updated travel activity data such as vehicle populations, vehicle type, and fleet age from metropolitan planning organizations (MPOs) and estimates emissions for diesel trucks, buses and gasoline powered vehicles (as three different modules). It applies annual average emission factors, adjusts for changes in the fuel economy and provides estimates for different seasons on a regional basis. For each county, we use daily emissions for 13 vehicle types (both gasoline and diesel fuels; Table 1) across aggregated vehicle speeds, and aggregated EMFAC model years. Currently, we use the modeled emissions estimates for the aggregated vehicle speeds but in the next version of this data product we will take into account the emissions due to different vehicle speed classes. Table 1 shows the 2012 EMFAC annual FFCO₂ emissions (tC yr^-1) for 13 vehicle types in the four counties. A detailed description of the 13 EMFAC vehicle types can be found under the FHWA 13—Category Scheme ^[19].

Table 1. Vehicle type classification and 2012 FFCO₂ emissions (tC/year) from EMFAC 2011 for the entire four counties within which lies the South Coast Air Basin.

EMFAC Vehicle Type		2012 FFCO2 emissions (tC/year)
Original	Final	Los Angeles	Orange	Riverside	San Bernardino
Passenger Cars	Passenger Cars	4,665,708	1,405,089	909,965	1,103,935
Light-Duty Trucks (0–3750 lbs)	Light Trucks	601,571	181,331	153,945	182,114
Light-Duty Trucks (3751–5750 lbs)	Light Trucks	2,131,467	713,799	453,826	556,188
Light-Heavy-Duty Trucks (8501–10000 lbs)	Single-Unit Trucks	571,635	181,084	149,467	201,903
Light-Heavy-Duty Trucks (10001–14000 lbs)	Single-Unit Trucks	88,442	25,585	24,877	32,234
Motorcycles	Motorcycles	14,137	5,351	4,947	6,960
Medium-Duty Trucks (5751–8500 lbs)	Single-Unit Trucks	1,997,160	739,904	558,597	643,960
Motor Homes	Single-Unit Trucks	28,950	11,443	12,347	14,532
Motor Coach & Other Buses	Buses	61,661	11,834	6,284	6,988
School Buses	Buses	15,955	4,776	5,563	5,836
Medium-Heavy Duty Trucks	Combination Trucks	337,100	108,520	64,034	78,287
Heavy-Heavy Duty Trucks	Combination Trucks	1,013,835	160,410	517,375	544,616
Urban Buses	Buses	165,240	32,704	12,612	14,426
	Total	11,692,860	3,581,830	2,873,840	3,391,977

 | Show Table

DownLoad: CSV

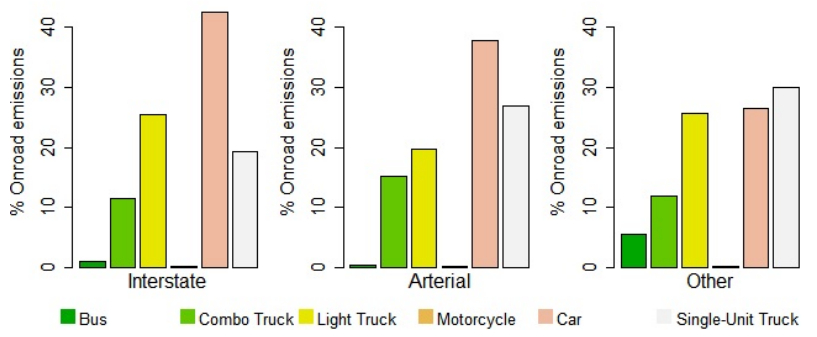
EMFAC emissions are produced in terms of vehicle types. To convert these estimates to categorization by road type, necessary for our space/time allocation (Figure 1, Table 2), we combined it with statewide data on road type-specific VKT and vehicle type-specific proportions of annual VKT on different road types (Tables 3 and 2 adapted from Tables VM-2 and VM-4) ^[20]. The statewide road and vehicle VKT proportions are available for three road and six vehicle types. Therefore, we aggregated the original 13 EMFAC vehicle types and 18 SCAG road types to match these six vehicle (Table 2) and three road (Table 4) types, respectively. Ideally we would have preferred to have information about the vehicle fleet composition for different road types in LA rather than for the entire state as currently available.

Figure 1. Annual vehicle FFCO2 emissions (EMFAC 2012) converted to road specific emissions based on state-level vehicle-road proportions (Source: Tables VM-2 and VM-4 revised in December 2012) ^[20]. Light Trucks include Light-Duty Trucks (0-3,750 lbs; e.g. passenger cars, light trucks, vans and sport utility vehicles) & Light-Duty Trucks (3,751-5,750 lbs; e.g. large passenger cars, vans, pickup trucks, and sport/utility vehicles). Single-Unit Trucks are Light-Heavy-Duty Trucks (8,501-10,000 lbs), Light-Heavy-Duty Trucks (10,001-14,000 lbs), Medium-Duty Trucks (5,751-8,500 lbs), and Motor Homes.

DownLoad: Full-Size ImgPowerPoint

Table 2. California state-wide proportional allocation of VKT among vehicle types. Adapted from Table VM-4 ^[20].

Road Type	Vehicle Type	Percent VKT
INTERSTATE SYSTEM	MOTORCYCLES	0.6
	PASSENGER CARS	61.5
	LIGHT TRUCKS	22.0
	BUSES	0.2
	SINGLE-UNIT TRUCKS	3.7
	COMBINATION TRUCKS	12.3
	TOTAL	100.0
OTHER ARTERIALS	MOTORCYCLES	0.7
	PASSENGER CARS	59.5
	LIGHT TRUCKS	28.3
	BUSES	0.2
	SINGLE-UNIT TRUCKS	4.1
	COMBINATION TRUCKS	7.4
	TOTAL	100.0
OTHER	MOTORCYCLES	0.3
	PASSENGER CARS	73.5
	LIGHT TRUCKS	23.0
	BUSES	0.4
	SINGLE-UNIT TRUCKS	1.5
	COMBINATION TRUCKS	1.4
	TOTAL	100.0

 | Show Table

DownLoad: CSV

Table 3. California state-wide VMT values specified by road type used in the LA megacity onroad FFCO₂ estimation. Adapted from Table VM-2 ^[20].

ROAD FUNCTIONAL TYPE	VMT(million miles)
INTERSTATE	85,772
OTHER FREEWAYS AND EXPRESSWAYS	53,407
OTHER PRINCIPAL ARTERIAL	74,394
MINOR ARTERIAL	58,100
MAJOR COLLECTOR	28,023
MINOR COLLECTOR	2,635
LOCAL	20,517
TOTAL	322,848

 | Show Table

DownLoad: CSV

Table 4. Crosswalk between SCAG and EMFAC road classifications.

SCAG Road Type	SCAG Code	EMFAC Road Type
Freeways	10	Interstate
HOV	20
Expressway/Parkway	30
Principal Arterial	40	Arterial
Minor Arterial	50
Major Collector	60	Collector
Minor Collector	70
Freeway to Freeway Connector	80	Interstate
Freeway to arterial	81
Arterial to freeway	82
Ramp Distributor	83
Ramp from Arterial to HOV	84
Ramp from HOV to Arterial	85
Collector distributor	86	Collector
Shared HOV Ramps to MF	87	Interstate
Truck only	89
Trucks -Urban	90
Centroid Connector	100	Local

 | Show Table

DownLoad: CSV

2.2. Annual traffic volume and road network

We used the annual average weekday traffic (AAWT) data from SCAG ^[21] for 18 functional road types (Table 4). The AAWT estimates are validated every four years against traffic count measurements from the California Department of Transportation (Caltrans) Performance Measurement System (PeMS) ^[22] and the Screenline Traffic Count Database ^[23]. The AAWT data is joined to SCAG's GIS road network (Figure 2) that is updated periodically. The road network completely represents all the actual roads in LA megacity except local roads. Local roads are represented by centroid connectors ^[24], a standard technique in transportation engineering when representing local roads. We assigned the traffic density (traffic count per segment length) of the nearest segment of the similar road type for road segments with missing traffic count. For the centroid connectors, we use traffic count instead of traffic density since centroid connectors are notional and their lengths have no meaning.

Figure 2. 2012 annual on-road FFCO₂ emissions (metric tonnes C per km) in the Los Angeles megacity classified by three major road types (interstate–red; arterial–orange; collector–green). Local roads are not shown in the map but their annual emissions are included in the table. Larger emissions are represented by thicker segments.

DownLoad: Full-Size ImgPowerPoint

2.3. Hourly traffic volume

The SCAG AAWT dataset reflects annual-level information. Therefore, we relied upon traffic count information from the Caltrans PeMS to distribute FFCO2 emissions in time. This dataset contains traffic count data collected at 5-minute intervals at measurement stations, primarily along freeways and less frequently along principal arterials, and aggregated across all traffic lanes. We used only those measurement stations on the mainline and HOV lanes of the freeways that had data for the entire year. We aggregated the 5-minute traffic counts to hourly data, and for each road type we estimated 8760 (365 days × 24 hours) fractions of annual traffic count by averaging over all measurement stations for that particular road type. Since traffic monitoring data was available primarily for interstates and some arterials, for the smaller road types that did not have traffic monitoring data we used the annual fraction data of the closest higher road type. Table 5 shows the data sources and the number of measurement stations included in calculating hourly fractions for each road type in each county. The hourly fractions remain the same for all segments of a road type in a county. For local roads, we estimated the weekday hourly fractions of traffic count from the SCAG AAWT data, which contained five distinct time periods within a 24-hour cycle (6–9 am, 9 am–3 pm, 3–7 pm, 7–9 pm, 9 pm–6 am). Hourly fractions on local roads during the weekend were derived from the county average of weekend hourly time fractions (see Table 5). The weekday and weekend hourly fractions were combined to form a complete week, and then replicated for all 52 weeks in the entire year. This was done because there was no significant seasonality in weekday and weekend traffic across the year as observed from PeMS data.

Table 5. Temporal profiles constructed for county-specific road types from PeMS and AAWT data.

Road type	Los Angeles	Orange	Riverside	San Bernardino
Interstate	n = 2236; PeMS	n = 1470; PeMS	n = 435; PeMS	n = 477; PeMS
Arterial	n = 14; PeMS	n = 7; PeMS	n = 4; PeMS	n = 2; PeMS
Collector	n = 6; PeMS	n = 2; PeMS	n = 3; PeMS	n = 3; PeMS
Local Roads	Uniform weekday; AAWT	Uniform weekday; AAWT	Uniform weekday; AAWT	Uniform weekday; AAWT

 | Show Table

DownLoad: CSV

2.4. Spatio-temporal disaggregation of annual emissions

We spatially allocated the road-and county-specific EMFAC annual FFCO₂ emissions estimates (from 2.1) to individual road segments based on their VKT as described in the steps below.

(1) We calculated VKT for all road types except centroid connectors. The segment length of centroid connectors is not physically-based since they are virtual roads denoted by straight lines joining the TAZ polygon boundary and centroid. Therefore, the length of centroid connectors was assigned a zero value, and VKT was calculated for all other road types as follows:

where L is the length of the road segment j.

(2) We added up segment AAWT to arrive at the total AAWT traffic count for the road type "Other" which includes collectors and local roads.

(3) The total FFCO₂ emissions for each road segment (within each county) were estimated by allocating the annual FFCO₂ emissions based on the proportion of segment VKT to the total VKT:

where E is the on-road FFCO₂ emissions for the segment j of road type r, N is the total number of road segments for the road type r, and TE is the total annual emissions for the road type r. The annual county-level vehicle emissions estimates were converted to road type estimates (TE^r) based on the proportions of road type VKT and vehicle type VKT for each road type (see subsection 2.1 in Materials and Methods).

(4) For the road type 'Other', which includes centroid connectors, major and minor collectors, and collector distributors, we estimated FFCO₂ emissions based on AAWT. Although collectors and collector distributors have VKT information, centroid connectors have only traffic count data. Hence, the FFCO₂ emissions for these two road types were estimated using AAWT as follows:

where TC is the AAWT traffic count and TE is the total annual emissions for road type "Other".

(5) Annual emissions per road segment were normalized by the segment length to arrive at emissions per road length for each road type. The physical length of each road segment was multiplied by the number of lanes incorporated from SCAG's network data. By taking into account the average number of lanes per road type, we have developed a more accurate metric for representing on-road emissions.

(6) Finally, the segment-specific annual FFCO₂ emissions were disaggregated at an hourly resolution using the 8760 average hourly fractions described above in subsection 2.3.

2.5. Hotspot and statistical analysis

The on-road FFCO₂ emissions estimates are logarithmically distributed so a log₁₀ transformation was used to normalize the distributions. Cumulative distribution function (CDF) of the on-road FFCO₂ emissions helped identify the top 5% of all non-local road segments with the highest FFCO₂ emissions (> 635.2 tC ln-km^-1). Subsequently, a CDF of only the arterial and collector roads helped identify the top 5% (> 419 tC ln-km^-1) of the highest-emitting road segments. GIS datasets of the truck and metrolink network, 2012 daily average truck volume data from Caltrans, and the 2005 landuse data from SCAG were used to identify potential drivers of high FFCO₂ emissions.

We did not have any information on the uncertainty estimates of the input datasets so we followed the root sum square method ^[25,26] where the uncertainty components are pooled to produce the combined uncertainty estimates. We bootstrapped ^[27] estimates of FFCO₂ and VKT per road length to estimate their means and 95% confidence intervals (CI) for the three road types. The standardized error on FFCO₂ emissions, E, was estimated for each of the three road types as follows:

where σ_i and σ_j are the estimates of uncertainty (CI) in FFCO₂km^-1 (from EMFAC) and VKT km^-1 (from SCAG), respectively, and μ_i and μ_i are the corresponding estimates of mean. Hence, these uncertainty estimates take into account the uncertainties in both the primary data sources.

3. Results

3.1. Spatial variations in annual FFCO₂ emissions

The 2012 annual on-road FFCO₂ emissions for the entire megacity, including local roads, are 19 million metric tonnes C (tC yr^-1). The relative contribution of each county within the LA megacity is as follows: Los Angeles-59%; Orange-19%; San Bernardino-11%; Riverside-11% (Table 6). The city of Los Angeles, with 17% of the inhabited area and 27% of the population in the megacity ^[28], accounts for 4.2 million tC yr^-1 or 25.4% of the total emissions. The next largest city contribution comes from the city of Long Beach with 0.51 million tC yr^-1, nearly 8x smaller. Figure 2 shows the on-road FFCO₂ emissions for the LA megacity categorized by road classification.

Table 6. County-and road-specific annual emissions for 2012.

2012 Onroad FFCO2 emissions (metric tonnes C/year) within the megacity
Road Type	Los Angeles	Orange	Riverside	San Bernardino
Interstate	4,538,925 (41%)	1,412,041 (39%)	853,119 (40%)	812,838 (37%)
Arterial	4,531,913 (41%)	1,499,246 (42%)	870,061 (41%)	989,321 (45%)
Other	2,066,813 (19%)	669,710 (19%)	383,811 (18%)	375,003 (17%)
County Total	11,137,651	3,580,997	2,106,991	2,177,162

 | Show Table

DownLoad: CSV

When examined according to road type, the interstate and arterial road types dominate the on-road FFCO₂ emissions, accounting for 81% of the total; the remaining 19% are on collectors and local roads. Though arterials and interstates account for a similar proportion of the total FFCO₂ emissions (41% and 40%, respectively), the total length of arterial roads is almost twice that of interstates. Hence, they have much lower FFCO₂ emissions per unit road length. Given the large traffic volume throughout the domain, interstates have high total and per unit road length emissions. Collectors have the lowest annual emissions, lower than local roads, and also the lowest FFCO₂ emissions per unit road length.

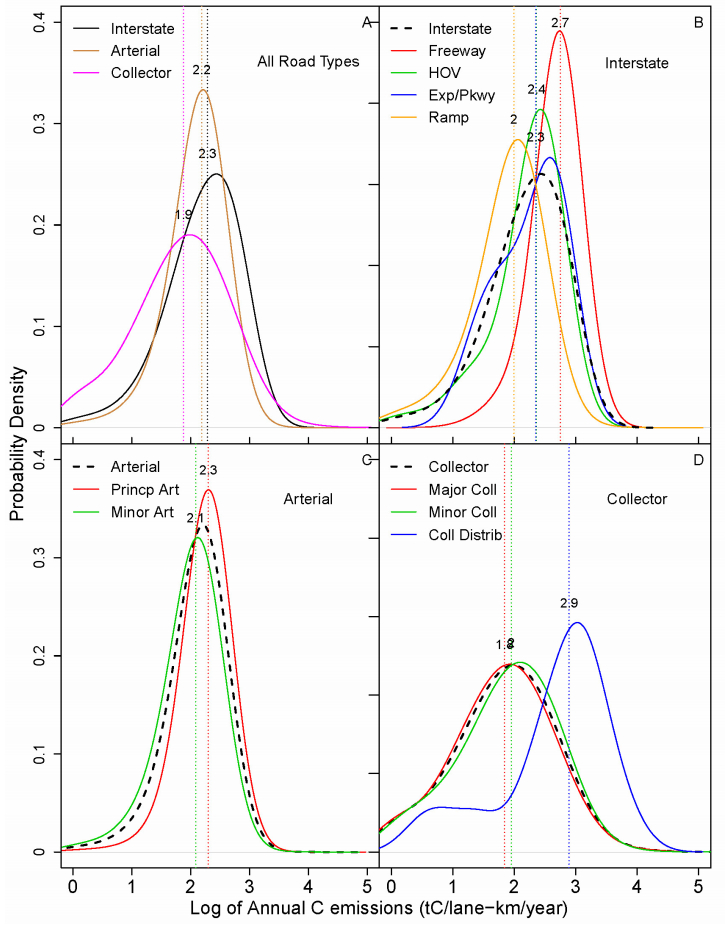
When normalized by distance and accounting for the number of lanes (lane-length), the probability density functions (PDF) of FFCO₂ road segment emissions for the major road types (and their sub-types) exhibit lognormal distributions (Figure 3, 3a). The interstates (Figure 3b) have the highest median normalized emission value followed by the arterials (Figure 3c) and collectors (Figure 3d), confirming the large traffic volume on interstates. Collectors & interstates have long-tailed distributions with more within-class variability in emissions. The wider distribution of the interstate and collector road types can be explained by examination of the sub-types within each. The interstate sub-types-freeway, HOV lanes, expressway/parkway, and ramp–have different median emissions values, some greater and some smaller than the parent interstate road type. Collectors have the most variation in emissions, with more extremely low and high estimates while arterials have the least variation.

Figure 3. Probability density function (PDF) of 2012 log₁₀ annual on-road FFCO₂ emissions per lane-length (tC lane-km^-1 yr^-1) for the (a) three major road types, (b) interstates, (c) arterials, and (d) collectors and their sub-types (interstates: freeways, HOVs, expressway/parkways, ramps; arterials: principle arterial, minor arterial; collector: major collector, minor collector, collector distributor). The vertical lines show the median of each distribution.

DownLoad: Full-Size ImgPowerPoint

Collectors have the least road length (length = 4,997 km or 14,163 lane-km; Figure 2) and the smallest median normalized emission value (log₁₀ median of 1.9; Figure 3A). They are low-to-moderate capacity roads that move traffic from local streets to arterial roads, and have potentially lower speed limits than arterials and interstates. The collector distributor is unique among the collector sub-types with a much higher median value of 2.9 (the highest median emissions compared to all other sub-road types). This is likely driven by the fact that collector distributors are transitional roadways between the main lanes of a freeway and frontage or arterial roads. Their purpose is to help increase traffic flow and speed and improve safety by reducing traffic weaving and conflict points arising from merging and diverging traffic ^[29]. This road type is a hybrid version of ramp and collector and though it has shorter length and fewer VKT, the emissions per VKT are the greatest (even larger than freeways), likely from traffic congestion.

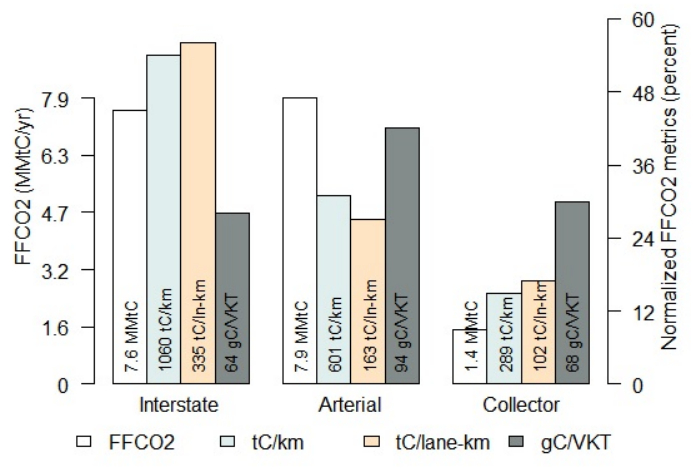
Figure 4 shows the total 2012 FFCO₂ emissions by major road type, emissions per road length (by linear physical road length and inclusive of all lanes), and the on-road FFCO₂ carbon emissions intensity (ratio of FFCO₂ emissions to vehicle kilometers travelled -gC/VKT). The three emissions metrics progressively account for physical road length, total number of lanes, and the traffic volume.

Figure 4. 2012 total annual FFCO₂ emissions (million metric tons C; primary Y-axis) and normalized FFCO₂ emissions metrics (per road length, per lane length, per vehicle distance travelled; secondary Y-axis) in the LA megacity for the three major road types. The normalized emissions metrics for each road type, with their dissimilar ranges, are represented as percent of the total of all the road types. For instance, the interstates have the highest emissions per road length (1060 tC/km) and when accounting for the number of lanes as well, their emissions per lane length (335 tC/lane-km) reduces by a factor of 3, the mean number of lanes for interstates. Local roads are not included (see text).

DownLoad: Full-Size ImgPowerPoint

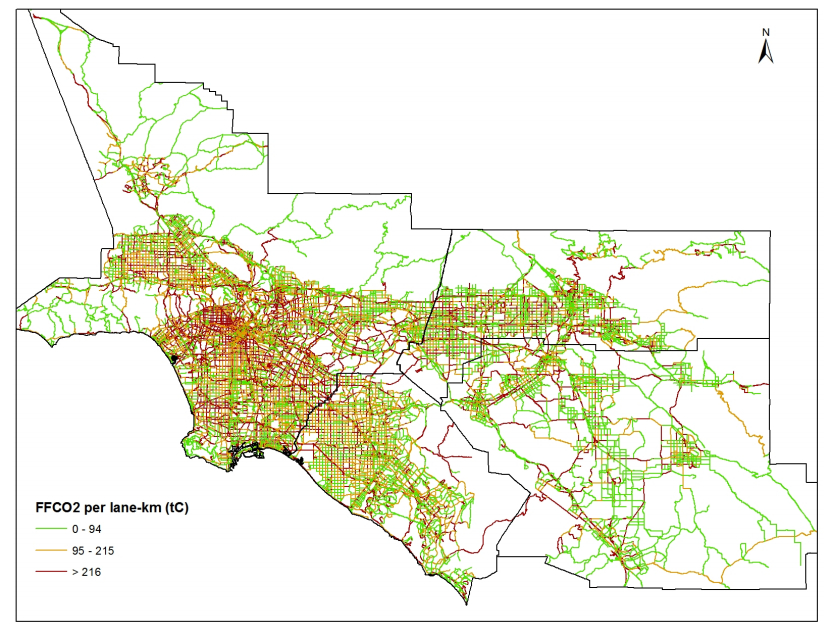
In the LA megacity, interstates have a mean of 3 lanes, arterials have 4 and collectors have 3. The contrast between normalization by physical road length only versus length and number of lanes incorporates these differences and provides greater insight. The emissions per road length decreased by a factor equivalent to the average number of lanes per road type. Having a larger number of lanes reduces the emissions per lane-length. In contrast to Figure 2 where emissions are depicted per unit of physical road length, we characterized the spatial distribution of on-road FFCO₂ emissions in the LA megacity by FFCO₂ per lane-length (Figure 5). The highest emissions are concentrated in the downtown area irrespective of the road type and, many of the freeways show lesser emissions due to the fact that freeways generally have a large number of lanes. Therefore, normalizing by the number of lanes rather than just the physical length of the road provides an additional piece of information on on-road emissions.

Figure 5. 2012 annual onroad FFCO₂ emissions normalized by lane-length. (tC per lane-km) in the LA megacity. The emissions are displayed in three quantile classes.

DownLoad: Full-Size ImgPowerPoint

Because the arterial road type contains the largest amount of total on-road FFCO₂ emissions (47% of the total on-road emissions from all road types except local) and a proportionally smaller amount of VKT (37% of total VKT), it has the largest FFCO₂ emissions intensity value (94 gC/VKT). These results imply that arterial roads are comprised of a vehicle fleet with a lower-average fuel economy and/or the vehicles on these roads are experiencing a proportionately larger amount of stop-and-go driving. By contrast, both the interstate and collector road types have nearly the same carbon emissions intensity at 64 and 68 gC/VKT, respectively. Interstates have 3.3x higher FFCO₂ emissions per ln-km than collectors because of the large traffic volume, greater physical length and number of lanes. But overall, interstates and collectors have similar C emission intensities, likely due to them having the same fleet makeup and similar driving conditions.

3.2. Emissions hotspots

Table 7 and Figure 6 present an analysis of the largest 5% of total on-road FFCO₂ emissions in the Los Angeles megacity in an attempt to explore the spatial pattern and potential common underlying attributes driving these large FFCO₂ emissions. The largest 5% are represented by road segments with annual FFCO₂ emissions exceeding 635.2 tC ln-km^-1 (Table 7). Interstates dominate this high-emitting cohort in terms of FFCO₂ emissions (76.5% of the cohort) followed by collectors and arterials (Figure 6a). Overall, the highest-emitting road segments are spread out across the entire megacity, with 67% of the FFCO₂ emissions from this cohort occurring in the Los Angeles county and 18% in the Orange county. If we exclude interstates and extract the top 5% of on-road FFCO₂ emissions (> 419 tC ln-km^-1; Figure 6b), we observe that arterials and collectors have similarly high emissions though collectors have a higher VKT than arterials (Table 7). These high-emitting arterials and collectors mostly occur in the more developed land use classes (not shown here) and densely populated areas of the megacity, especially in and around downtown Los Angeles.

Table 7. Summary of the 2012 annual onroad FFCO₂ emission hotspots (the largest 5% by road class in tC ln-km^-1) in the Los Angeles megacity, with and without the interstate road type.

Road Class	Road length (ln-km)	VKT (billion km)	FFCO2 (103 tC)	tC/ln-km	gC/VKT
ALL ROAD TYPES (Top 5%)
Interstate	4,212 (86%)	49 (76%)	3,130 (76.5%)	743	64
Arterial	281 (6%)	4 (6.5%)	389 (9.5%)	1,387	95
Collector	424 (8%)	11 (17.5%)	574 (14%)	1,354	52
TOTAL	4,917	63.87	4,094
ROAD TYPES OTHER THAN INTERSTATES (Top 5%)
Arterial	1,087 (61%)	8 (40%)	779 (52%)	717	96
Collector	708 (39%)	12 (60%)	721 (48%)	1,019	60
TOTAL	1,794	20	1,500

 | Show Table

DownLoad: CSV

Figure 6. 2012 annual on-road FFCO₂ emission hotspots (tC ln-km^-1) in the Los Angeles megacity. (a) spatial distribution of the largest 5% shown in three quantile intervals for all road types except local; (b) spatial distribution of the largest 5% without the interstate road type (only arterials and collectors).

DownLoad: Full-Size ImgPowerPoint

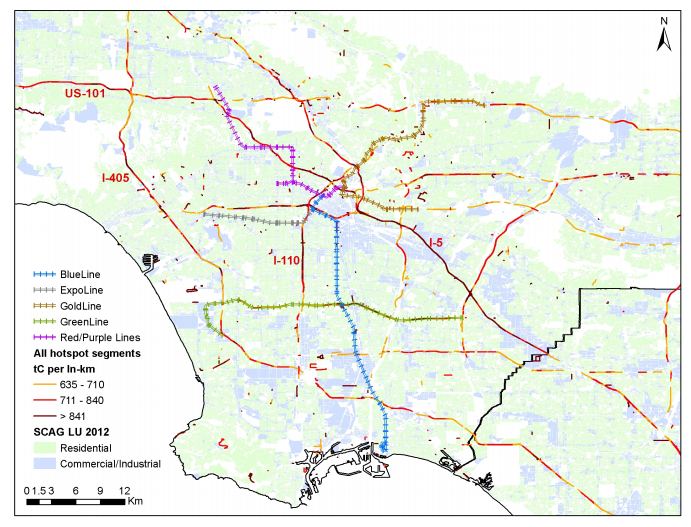
We combined ancillary GIS datasets such as landuse ^[21], the LA metro network ^[30] and on-road emissions hotspots (Figure 6a) for a preliminary spatial analysis of emissions hotspots in conjunction with alternate transportation modes. Additionally, bus routes and temporal information on the alternate transportation modes can be incorporated. Temporal information can further help in narrowing down to specific mitigation strategies, say for rush-hour traffic or mid-morning long-distance truck traffic. The emissions hotspots along sections of the I-5 in east LA, I-110 in south LA, and US-101 and I-405 in north-west LA indicate the need for alternative transportation options (Figure 7). On the other hand, the Red/Purple Lines in northern LA and Gold Metro Line in east LA currently operate along sections of US-101 and I-5 that have high emissions. Clearly, there is a need for additional reinforcement to ease the traffic. Perhaps, the eastern ends of the Gold and Green Lines need to be connected to reduce the traffic congestion along that section of I-5. Having such updated spatio-temporal information on segment-specific traffic emissions can help plan effective strategies for mitigation of FFCO₂ emissions.

Figure 7. Preliminary GIS analysis to explore on-road emissions hotspots in conjunction with the current LA metro network, identify potential drivers, and prioritize strategies for emissions reduction. The landuse data from SCAG identifies residential vs. commercial/industrial areas. Additional layers such as bus and truck routes can be further added for a more comprehensive analysis.

DownLoad: Full-Size ImgPowerPoint

3.3. Temporal variations in on-road FFCO₂ emissions

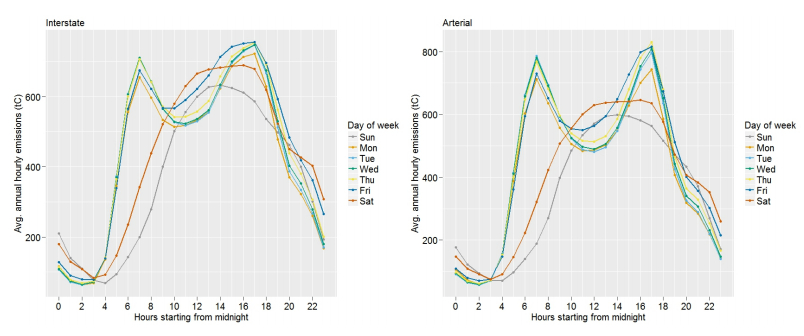
In addition to the large spatial variation in on-road FFCO₂ emissions in the LA megacity, there are similarly large variations in time. Because the PeMS monitoring stations are limited to interstates and arterials, we estimated sub-annual time structure on these road types only. There is little seasonal variation (~ 10% of mean levels) in on-road emissions and hence we focus only on diurnal and day-of-week variations. This limited variation was also noted by McDonald ^[32].

Weekday peak hour emissions (6–8 am and 4–6 pm; 636–717 tC hr^-1) were 41–59% higher than the 24 hour mean (451 tC hr^-1) for interstates. The afternoon emissions minima (10 am–12 pm; ~ 543 tC hr^-1) was 20% higher than the 24 hour mean. For arterials, the morning/evening maxima were 57–67% higher and the afternoon minima 17% higher than the 24 hour mean (439 tC hr^-1; Figure 8). Of the seven days of the week, Tuesday, Wednesday and Thursday exhibit the greatest similarity in time structure. Monday evening rush hour exhibits the smallest peak (723 tC hr^-1) while Friday evenings show the largest (756 tC hr^-1). Marr and Harley ^[13] also observed similar trends in weekday rush hour traffic with a higher peak on Fridays than on Mondays and attributed these trends to commuter traffic.

Figure 8. 2012 average hourly on-road FFCO₂ emissions (tC hr^-1) for interstates and arterials in the LA megacity. Emissions represent an unweighted spatial average of all road segments in the domain.

DownLoad: Full-Size ImgPowerPoint

Interstates and arterials weekend emissions are 85–88% of the weekday values and have a single maximum extending from 10am to 6pm rather than the morning and evening rush hour maxima. This change in the weekend time structure is likely driven by the decrease in 9–to–5 commuters. Traffic emissions on Saturdays are larger (626–666 tC hr^-1) and more broadly peaked (11 am–6 pm) than on Sundays (569–597 tC hr^-1; Figure 8). These weekend emission patterns are influenced more by commuter than commercial vehicle traffic ^[31,32].

Interstates have a smaller weekday difference (~ 136 tC) between morning rush hour and midday maximum emissions compared to arterials (~ 248 tC). This is perhaps attributable to greater commercial traffic on interstates in the afternoons (Figure 8). The greater difference between morning and midday emissions on arterials may be due to a higher proportion of commuter traffic, a less fuel efficient fleet mixture, or sub-optimal driving conditions such as congestion or stop-and-go driving conditions ^[33]. McDonald et al. ^[31] disaggregated these diurnal patterns into two vehicle types—passenger vehicles and commercial trucks—and observed that trucks have a single midday peak unlike the morning and evening commuter peaks from passenger vehicles. Therefore, the pattern observed in this study for urban interstates likely reflects the combined effect of passenger vehicles and trucks. Also, since our study area is primarily urban, our results are not expected to reflect the rural temporal patterns found in McDonald et al. ^[31].

3.4. Uncertainty estimates and comparison with existing datasets

This study integrated data from SCAG's traffic count data, CARB's EMFAC2011, and CALTRANS PeMS to estimate on-road FFCO₂ emissions in the LA megacity domain. These input data have inherent uncertainties. Errors in these inputs will propagate to the on-road FFCO₂ emissions estimates ^[34]. Moreover, gap-filling the input data can add further uncertainty. Errors in estimated emissions can also arise because of the assumptions incorporated in our methods. We applied state-level VKT proportions to convert county-specific EMFAC vehicle emissions to road emissions. However, the proportions in the LA megacity, the most urbanized region in California, can deviate from the state level average. In a future version, we could use vehicle registration data of LA to see how they compare to the state vehicle proportions or perhaps from SCAG's screenline count data.

Since the segment FFCO₂ estimates are derived from VKT and FFCO₂ emissions per road type, uncertainties in either of these terms lead to uncertainty in the final estimated emissions. Exact estimates of errors in the input data are not available. We assumed that bootstrapped confidence interval (CI) will provide a reliable, alternate measure of uncertainty. From analysis of the VKT data, we found that the mean and 95% CI of VKT km^-1 for interstates, arterials, and collectors are 13.9 ± 0.4, 6.9 ± 0.1, 2.4 ± 0.1 million km, respectively (see Methods section). These equate to the uncertainty estimates of 2.7, 0.8, and 2.0% of the mean, respectively. Similarly, the mean and CI of FFCO₂ km^-1 were 898 ± 19,653 ± 3, and 794 ± 144 tC km^-1 for interstates, arterials and collectors, respectively. This translates to the uncertainty estimates of 2.1, 0.5, and 18.0% of the mean. The higher uncertainty of collector road type stems from the fact that it includes collector distributors that have significantly higher mean FFCO₂ emissions per lane-length than major and minor collectors (Figure 3). Combining the uncertainty in VKT and FFCO₂ emissions per road length, according to Equation 4, leads to an overall uncertainty of 3.5, 0.9, and 18% in FFCO₂ emissions for interstates, arterials, and collectors, respectively.

Comparison of Hestia version 1.0 on-road emissions estimates with two existing on-road emissions inventories, DARTE ^[35] and FIVE ^[31] show differences due to data inputs and estimation methodologies. DARTE is a 1 km, annual on-road FFCO₂ emissions inventory for 1980–2012 derived from roadway-level traffic counts from the highway performance monitoring system (HPMS) and state-level VMT for collectors and local roads. The annual roadway-level VMT was partitioned by roadway functional classes and vehicle classes from the FHWA's Highway Statistics for each county in the US. VMT and state-level fuel consumption data was then converted to CO₂ emissions using emissions factors from US Environmental Protection Agency (EPA). The primary difference between the Hestia and DARTE approaches is that Hestia has finer spatial and temporal resolution data inputs such as traffic count data from SCAG, hourly traffic counts for highways, and modeled emissions estimates from EMFAC, a California-specific traffic emissions model. FIVE, on the other hand, uses state-level fuel sales data apportioned to finer spatial scales based on traffic count monitoring and road density. It is a 500 m gridded inventory with an hourly temporal resolution.

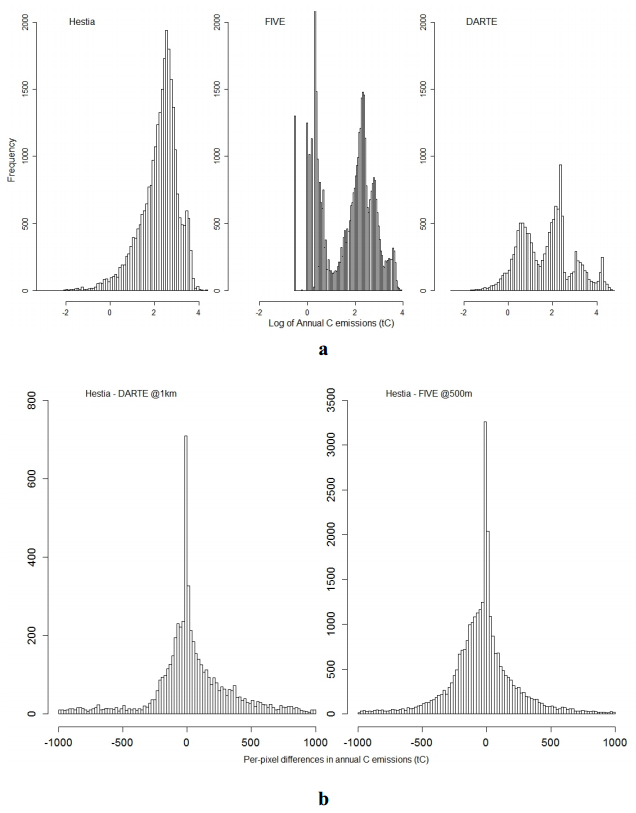
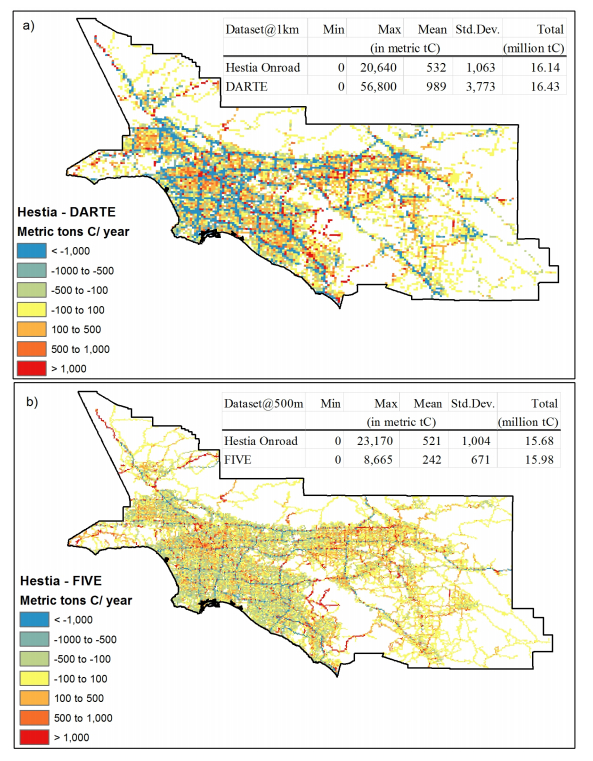
For the LA megacity, the overall annual estimates of FFCO₂ emissions from Hestia, FIVE and DARTE are 15.68, 15.98 and 16.43 tC respectively. The total annual estimates are quite similar but the finer spatial distributions are distinctly different for the three datasets (Figure 9a). Hestia, FIVE and DARTE have mean emissions of 520.80,242.30 and 989.20 tC, and median estimates at 192. 10, 3.44 and 15.70, respectively. The methods and data sources to spatially distribute the FFCO₂ emissions vary considerably for each dataset. Compared to Hestia's unimodal distribution, FIVE and DARTE have bimodal and multi-modal distributions. Both FIVE and DARTE use different spatial proxies to assign emissions to the large and small road types. FIVE has a large number of road segments with low emissions (log₁₀ of annual emissions between 0 and 1) and is likely to be an artifact. DARTE has some unusually high estimates (log₁₀ of annual emissions greater than 4) that might be because of its coarser resolution. The log₁₀ per-pixel differences between Hestia and DARTE at 1 km and Hestia and FIVE at 500 m show a higher proportion of road segments with zero and near-zero differences (Figure 9b). However the longer tails at either ends indicate that the actual (non-logarithmic) differences between the datasets are rather high.

Figure 9. Histograms showing the data distribution of the annual FFCO₂ emissions estimates from the three datasets in the top panel (a), and that of the differences between Hestia and DARTE, and Hestia and FIVE in the lower panel (b).

DownLoad: Full-Size ImgPowerPoint

A visual inspection of the difference maps indicates that the largest differences between Hestia and DARTE at 1 km are present in the interstate and arterial road types, and the correlation coefficient, r between these two datasets is 0.49 (Figure 10a). These differences are mainly because Hestia data inputs include Southern California-specific emissions estimates and traffic volume information from EMFAC and SCAG, respectively as opposed to the national-level HPMS data in case of DARTE. Another factor could be the resampling of Hestia estimates from 500 m to 1 km so as to be comparable to DARTE. By contrast, the Hestia estimate exhibits greater correlation to the FIVE emissions (correlation coefficient, r = 0.72; Figure 10b) with lower differences per road type.

Figure 10. Spatial difference maps of the Hestia on-road FFCO₂ emissions estimates with (a) DARTE at 1km and with (b) FIVE at 500m. The red and the blue colors highlight areas with the most differences.

DownLoad: Full-Size ImgPowerPoint

4. Discussion and Conclusions

4.1. On-road FFCO₂ emissions hotspots and their policy implications

Emissions per unit area is a frequently reported FFCO₂ emissions metric particularly when reporting emissions in gridded form ^[31] where its accuracy depends on the spatial resolution of the grid cell, among other things. Quantifying emissions by linear road length normalizes on-road FFCO₂ emissions by physical length of road segments preserving the inherent spatial resolution of the road network and allocating the emissions onto the road itself ^[36]. Furthermore, we quantified on-road FFCO₂ emissions by physical road length, road lane-length and vehicle kilometers traveled (VKT, the carbon intensity), thus providing much greater insight into actual driving conditions and a more comprehensive basis for comparison within the on-road landscape. For example, the carbon emissions intensity isolates difference due to the mean fuel economy (miles per gallon, MPG) of all vehicles travelling on a particular road with inherent fleet composition or driving characteristics.

We find that arterials have the highest carbon emissions intensity (94 gC VKT^-1) compared to interstates and collectors. Arterials connect urban centers and transfer traffic from collectors to interstates, thus providing greater levels of access (in terms of travel origin and destination) to the traveler while interstates offer more mobility and higher speed limits than arterials ^[37]. The very nature of the arterial road types implies that the lower traffic speeds and greater congestion could be a significant driver of greater FFCO₂ emissions intensity on these roads. Barth and Boriboonsomsin ^[33] found that vehicles on arterials in Southern California travel at mean traffic speeds of less than 80 kph in contrast to interstates where the mean travel speed is 72–121 kph. Based on field observations, they estimated that an average trip in Southern California produces FFCO₂ emissions of ~ 205 g km^-1 corresponding to ~ 11 km per liter (26 miles per gallon) of fuel economy. However, for average vehicle speeds of 8–40 kph (such as on arterials) FFCO₂ emissions can increase 2x (~ 466 g km^-1). Despite arterials having a lower VKT, their higher FFCO₂ emissions seem to be additionally influenced by fleet composition. Arterials have 7.6% more single-unit trucks and 3.6% more combination trucks (multiple cargo units) than interstates (Figure 1) and are more likely to occur in the less urbanized areas of the megacity. These diesel vehicles have lower fuel economy than the equivalent gasoline-based vehicles ^[38,39]. Diesel engines are actually more fuel-efficient than equivalently sized gasoline engines but because of their larger size, they tend to have a lower fuel economy. Fleet age, especially in passenger (light-duty) vehicles, and fuel efficiencies on urban roads are more variable, and have higher uncertainties ^[34]. These could be contributing factors for the higher C emissions intensity of arterials especially in more urbanized areas.

The finer spatial differences between Hestia version 1.0 on-road, DARTE and FIVE FFCO₂ emissions estimates (Figures 9 and 10) are attributable to differences in data sources and proxies used to spatially allocate the emissions. Estimates from these three datasets can help define the uncertainty in emissions per road segment. Additional ground data is required to further analyze and compare these datasets so as to identify inadequacies of each dataset and potential measures to reduce the uncertainties. It must be noted here that, unlike DARTE and FIVE, we further identified FFCO₂ emissions hotspots in the study area, and the Hestia on-road estimates presented here are part of a larger, comprehensive dataset that includes other sectoral FFCO₂ emissions. The high-emitting cohort (road segments with FFCO₂ emissions > 635 tC ln-km^-1) is dominated by specific freeways, arterials and collectors. The high-emitting cohort sans interstates is equally dominated by arterials and collectors (including collector distributors; Table 7 and Figure 6) in terms of emissions. Therefore, these arterials have a clearly identifiable potential for FFCO₂ emissions mitigation. Further, we see that collector distributors are outliers in terms of FFCO₂ emissions per lane-km (sub-road type with the highest median emissions of log₁₀ median value of 2.9; Figure 3). Given the nature of the collector distributor road type, further information from the transportation engineering and policy communities would be required to determine the scope for emissions mitigation on this road type. Focusing on just this high-emitting cohort should therefore be useful to policy makers interested in understanding the detailed spatial and temporal distribution of FFCO₂ and its relationship to ancillary data in order to develop the most effective FFCO₂ mitigation policies. The temporal details of these high-emitting segments also offer important information for choosing optimal on-road FFCO₂ mitigation options. For instance, it may be useful to focus on areas with large persistent emissions versus those with intermittent emissions. Combining ancillary GIS datasets such as adjoining landuse, truck routes, and proximity to other modes of transportation with this FFCO₂ emissions data product can provide insights on potential drivers of high-emitting road segments (Figure 7). Hence, a proximity analysis of the high-emitting segments with other modes of transportation could help determine where new metro or bus routes can be planned, and at what frequency such services be provided to mitigate the traffic congestion and FFCO₂ emissions on those road segments.

Based on its 2012–2035 RTP/SCS plan for per capita transportation emissions reductions in the LA megacity, SCAG has defined some performance metrics to monitor progress towards these goals such as a decrease in average trip length by ~1.61 km/day, a per capita VKT decrease of 4.82 km/day, and a 5–15% increase in availability of transportation modes such as HOV lanes, bike/walk paths and public transit routes. Also, the 153 cities within LA megacity are increasingly developing and implementing climate change mitigation plans to reduce FFCO₂ emissions and other atmospheric pollutants ^[3,4]. Cities can access our link-level emissions estimates to quantitatively assess the current emissions and develop their mitigation strategies. Our on-road emissions estimates, when updated annually, can help monitor changes in VKT and associated emissions at the link level. Understanding the space and time distribution of FFCO₂ emissions and their magnitude across the LA megacity road network (as discussed above) offers the ability to quantitatively compare different mitigation options, and monitor the implementation of such policy goals.

4.2. Future work

While this data product provides the first, high-resolution, hourly estimate of on-road FFCO₂ emissions in the Los Angeles megacity, there are a number of improvements that could be made. Incorporating traffic monitoring data for collectors and local roads from SCAG's Screenline count database could improve temporal information for smaller road types. Similarly, maintaining the spatial content of the temporal information in the larger road types rather than averaging within a road type, would offer insight into how the rush hours and other high-emission traffic events vary in space. The translation from FFCO₂ emissions quantified in vehicle classes to emissions quantified by road type utilized state averages. Performing this with information specific to the LA megacity would likely alter the results, given how much variation in on-road activity exists in the State of California. Accurate data on fleet composition can also improve the assessment of congestion and fleet fuel economy.

Barth and Boriboonsomsin ^[33] reported that driving behavior, road type and traffic congestion influence FFCO₂ emissions per road length and also, showed the effect of vehicle speed on FFCO₂ emissions. Mean travel speed, in turn, is influenced by the level of traffic congestion and also the road type as shown by their study. We used the EMFAC emissions from aggregated vehicle speed (mean of modeled emissions across all speed classes) rather than for different speed classes in this version but hope to incorporate the different speed classes and their associated emissions in the future. The EMFAC model also includes FFCO₂ emissions from starting, running, and idling processes for different vehicle-speed classes. Incorporating such information will be useful to further disaggregate the segment FFCO₂ emissions and achieve a deeper understanding of the carbon emissions intensity observed for different road types. Congestion information can be directly retrieved from the embedded freeway loop sensors similar to the work by Barth and Boriboonsomsin. Emission-speed relationships assuming an average fleet were modeled from historical freeway loop sensor data. Current loop sensor data applied to these emission-speed curves can inform about emissions due to traffic congestion.

4.3. Conclusions

This study presents on-road FFCO₂ emissions estimated for the Los Angeles megacity for individual road segments and for each hour of the year 2012. We define three different metrics to characterize FFCO₂ emissions for the three road classes, and identify emissions hotspots in space and time. Such finely resolved emissions estimates can help cities design and monitor emissions mitigation strategies. These on-road emissions estimates, combined with other sectoral estimates in Hestia 1.0, provide a-priori inputs to modeling of atmospheric CO₂ mixing ratios in the LA air basin.

Acknowledgments

This research is supported by the National Institute of Standards and Technology (NIST) Greenhouse Gas Measurement Science Program through interagency agreement with NASA, and was performed at the Jet Propulsion Laboratory, California Institute of Technology under contract with the NASA. The data used are listed in the references, tables, supplements and PANGAEA repository at URL: https://doi.pangaea.de/10.1594/PANGAEA.869894.

Conflict of Interest

The authors declare they have no conflicts of interest in this article.