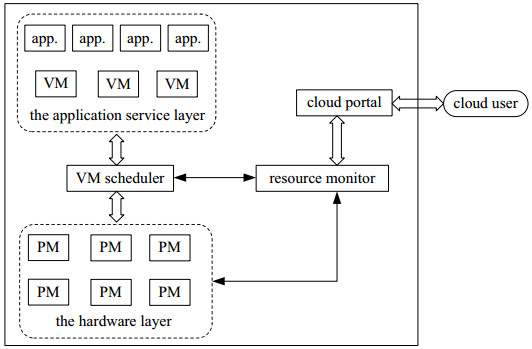
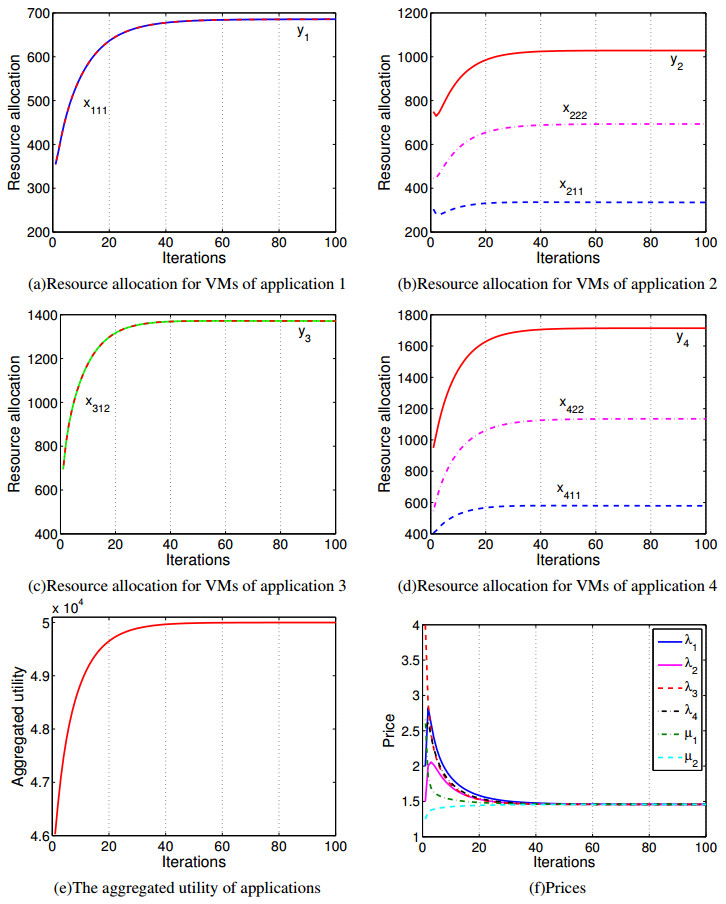
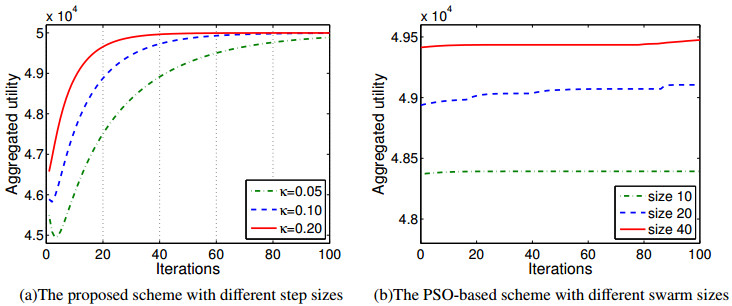
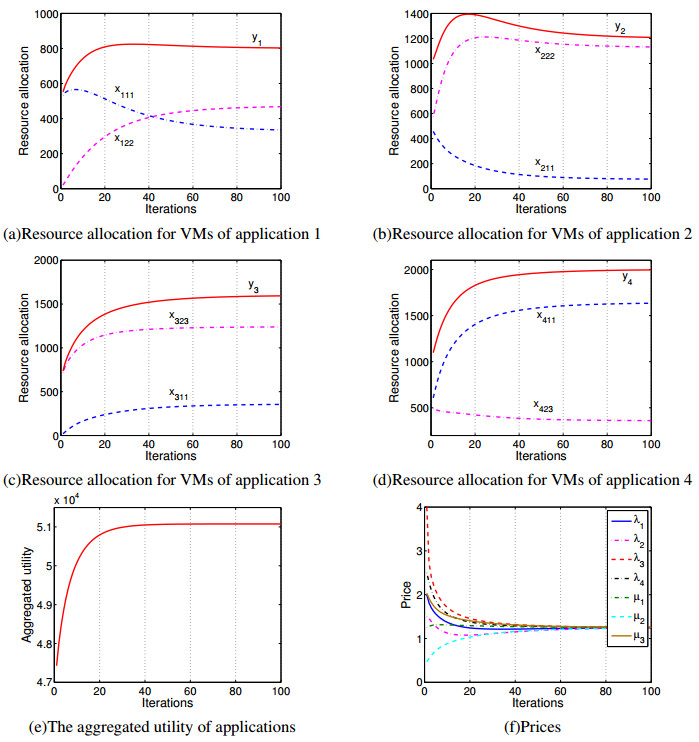
The emergence of cloud computing can help enterprises reduce their hardware and software investment and save their own operation and maintenance costs, thus more and more enterprises deploy their applications into the cloud. Generally, components of enterprise applications are resided in virtual machines and then hosted by physical machines. In order to achieve the efficiency and utilization of physical machines, reasonable virtual machines placement becomes very important. In this paper we propose a scheme of resource allocation model for virtual machines placement and investigate it with convex optimization approach. We also present a heuristic algorithm to achieve the optimal resource allocation and discuss its equilibrium and stability by applying the asymptotic stability of the continuous dynamic system of Lyapunov stability theory. Finally, we give some numerical examples to illustrate the performance of the resource allocation scheme and confirm its convergence with a certain number of iterations.
Dedicated to Giuseppe Mingione on the occasion of his 50th birthday, with admiration.
1.
Introduction
In this paper we provide a limiting partial regularity criterion for vector-valued minimizers u:Ω⊂Rn→RN, n≥2, N>1, of nonhomogeneous, quasiconvex variational integrals as:
with standard p-growth. More precisely, we infer the optimal [31, Section 9] ε-regularity condition
and the related borderline function space criterion
This is the content of our main theorem.
Theorem 1.1. Under assumptions (1.6)1,2,3, (1.7) and (1.10), let u∈W1,p(Ω,RN) be a local minimizer of functional (1.1). Then, there exists a number ε∗≡ε∗(data)>0 such that if
then there exists an open set Ωu⊂Ω with |Ω∖Ωu|=0 such that
Moreover, the set Ωu can be characterized as follows
where E(⋅) is the usual excess functional defined as
We immediately refer to Section 1.2 below for a description of the structural assumptions in force in Theorem 1.1. Let us put our result in the context of the available literature. The notion of quasiconvexity was introduced by Morrey [38] in relation to the delicate issue of semicontinuity of multiple integrals in Sobolev spaces: an integrand F(⋅) is a quasiconvex whenever
Under power growth conditions, (1.5) is proven to be necessary and sufficient for the sequential weak lower semicontinuity on W1,p(Ω;RN); see [1,4,35,36,38]. It is worth stressing that quasiconvexity is a strict generalization of convexity: the two concepts coincide in the scalar setting (N=1), or for 1-d problems (n=1), but sharply differ in the multidimensional case: every convex function is quasiconvex thanks to Jensen's inequality, while the determinant is quasiconvex (actually polyconvex), but not convex, cf. [24, Section 5.1]. Another distinctive trait is the nonlocal nature of quasiconvexity: Morrey [38] conjectured that there is no condition involving only F(⋅) and a finite number of its derivatives that is both necessary and sufficient for quasiconvexity, fact later on confirmed by Kristensen [29]. A peculiarity of quasiconvex functionals is that minima and critical points (i.e., solutions to the associated Euler-Lagrange system) might have very different behavior under the (partial) regularity viewpoint. In fact, a classical result of Evans [22] states that the gradient of minima is locally Hölder continuous outside a negligible, " singular" set, while a celebrated counterexample due to Müller and Šverák [39] shows that the gradient of critical points may be everywhere discontinuous. After Evans seminal contribution [22], the partial regularity theory was extended by Acerbi and Fusco [2] to possibly degenerate quasiconvex functionals with superquadratic growth, and by Carozza, Fusco and Mingione [8] to subquadratic, nonsingular variational integrals. A unified approach that allows simultaneously handling degenerate/nondegenerate, and singular/nonsingular problems, based on the combination of A-harmonic approximation [21], and p-harmonic approximation [20], was eventually proposed by Duzaar and Mingione [19]. Moreover, Kristensen and Mingione [30] proved that the Hausdorff dimension of the singular set of Lipschitz continuous minimizers of quasiconvex multiple integrals is strictly less than the ambient space dimension n, see also [5] for further developments in this direction. We refer to [3,15,16,25,26,27,28,37,41,42] for an (incomplete) account of classical, and more recent advances in the field. In all the aforementioned papers are considered homogeneous functionals, i.e., f≡0 in (1.1). The first sharp ε-regularity criteria for nonhomogeneous quasiconvex variational integrals guaranteeing almost everywhere gradient continuity under optimal assumptions on f were obtained by De Filippis [12], and De Filippis and Stroffolini [14], by connecting the classical partial regularity theory for quasiconvex functionals with nonlinear potential theory for degenerate/singular elliptic equations, first applied in the context of partial regularity for strongly elliptic systems by Kuusi and Mingione [33]. Potential theory for nonlinear PDE originates from the classical problem of determining the best condition on f implying gradient continuity in the Poisson equation −Δu=f, that turns out to be formulated in terms of the uniform decay to zero of the Riesz potential, in turn implied by the membership of f to the Lorentz space L(n,1), [9,31]. In this respect, a breakthrough result due to Kuusi and Mingione [32,34] states that the same is true for the nonhomogeous, degenerate p-Laplace equation–in other words, the regularity theory for the nonhomogeneous p-Laplace PDE coincides with that of the Poisson equation up to the C1-level. This important result also holds in the case of singular equations [18,40], for general, uniformly elliptic equations [6], up to the boundary [10,11,13], and at the level of partial regularity for p-Laplacian type systems without Uhlenbeck structure, [7,33]. We conclude by highlighting that our Theorem 1.1 fits this line of research as, it determines for the first time in the literature optimal conditions on the inhomogeneity f assuring partial BMO-regularity for minima of quasiconvex functionals expressed in terms of the limiting function space L(n,∞).
1.1. Outline of the paper
In Section 2 we recall some well-known results from the study of nonlinear problems also establishing some Caccioppoli and Gehring type lemmas. In Section 3 we prove the excess decay estimates; considering separately the nondegenerate and the degenerate case. Section 4 is devoted to the proof of Theorem 1.1.
1.2. Structural assumptions
In (1.1), the integrand F:RN×n→R satisfies
for all z∈RN×n, Λ≥1 being a positive absolute constant and μ:[0,∞)→[0,1] being a concave nondecreasing function with μ(0)=0. In the rest of the paper we will always assume p≥2. In order to derive meaningful regularity results, we need to update (1.5) to the stronger strict quasiconvexity condition
holding for all z∈RN×n and φ∈W1,p0(B,RN), with λ being a positive, absolute constant. Furthermore, we allow the integrand F(⋅) to be degenerate elliptic in the origin. More specifically, we assume that F(⋅) features degeneracy of p-Laplacian type at the origin, i.e.,
which means that we can find a function ω:(0,∞)→(0,∞) such that
for every z∈RN×n and all s∈(0,∞). Moreover, the right-hand side term f:Ω→RN in (1.1) verifies as minimal integrability condition the following
which, being p≥2, in turn implies that
Here it is intended that, when p≥n, the Sobolev conjugate exponent p∗ can be chosen as large as needed - in particular it will always be larger than p. By (1.5) and (1.6)2 we have
with c≡c(n,N,Λ,p); see for example [35, proof of Theorem 2.1]. Finally, (1.7) yields that for all z∈RN×n, ξ∈RN, ζ∈Rn it is
see [24, Chapter 5].
2.
Preliminaries
In this section we display our notation and collect some basic results that will be helpful later on.
2.1. Notation
In this paper, Ω⊂Rn is an open, bounded domain with Lipschitz boundary, and n≥2. By c we will always denote a general constant larger than one, possibly depending on the data of the problem. Special occurrences will be denoted by c∗,˜c or likewise. Noteworthy dependencies on parameters will be highlighted by putting them in parentheses. Moreover, to simplify the notation, we shall array the main parameters governing functional (1.1) in the shorthand data:=(n,N,λ,Λ,p,μ(⋅),ω(⋅)). By Br(x0):={x∈Rn:|x−x0|<r}, we denote the open ball with radius r, centred at x0; when not necessary or clear from the context, we shall omit denoting the center, i.e., Br(x0)≡Br - this will happen, for instance, when dealing with concentric balls. For x0∈Ω, we abbreviate dx0:=min{1,dist(x0,∂Ω)}. Moreover, with B⊂Rn being a measurable set with bounded positive Lebesgue measure 0<|B|<∞, and a:B→Rk, k≥1, being a measurable map, we denote
We will often employ the almost minimality property of the average, i.e.,
for all z∈RN×n and any t≥1. Finally, if t>1 we will indicate its conjugate by t′:=t/(t−1) and its Sobolev exponents as t∗:=nt/(n−t) if t<n or any number larger than one for t≥n and t∗:=max{nt/(n+t),1}.
2.2. Tools for nonlinear problems
When dealing with p-Laplacian type problems, we shall often use the auxiliary vector field Vs:RN×n→RN×n, defined by
incorporating the scaling features of the p-Laplacian. If s=0 we simply write Vs(⋅)≡V(⋅). A couple of useful related inequalities are
and
where the constants implicit in " ≲", " ≈" depend on n,N,p. A relevant property which is relevant for the nonlinear setting is recorded in the following lemma.
Lemma 2.1. Let t>−1, s∈[0,1] and z1,z2∈RN×n be such that s+|z1|+|z2|>0. Then
with constants implicit in "≈" depending only on n,N,t.
The following iteration lemma will be helpful throughout the rest of the paper; for a proof we refer the reader to [24, Lemma 6.1].
Lemma 2.2. Let h:[ϱ0,ϱ1]→R be a non-negative and bounded function, and let θ∈(0,1), A,B,γ1,γ2≥0 be numbers. Assume that h(t)≤θh(s)+A(s−t)−γ1+B(s−t)−γ2 holds for all ϱ0≤t<s≤ϱ1. Then the following inequality holds h(ϱ0)≤c(θ,γ1,γ2)[A(ϱ1−ϱ0)−γ1+B(ϱ1−ϱ0)−γ2].
We will often consider the "quadratic" version of the excess functional defined in (1.4), i.e.,
In the particular case z0=(Dw)Bϱ(x0) (z0=(V(Dw))Bϱ(x0), resp.) we shall simply write E(w,(Dw)Bϱ(x0);Bϱ(x0))≡E(w;Bϱ(x0)) (˜E(w,(V(Dw))Bϱ(x0);Bϱ(x0))≡˜E(w;Bϱ(x0)), resp.). A simple computation shows that
Moreover, from (2.1) and from [23, Formula (2.6)] we have that
2.3. Basic regularity results
In this section we collect some basic estimates for local minimizers of nonhomogeneous quasiconvex functionals. We start with a variation of the classical Caccioppoli inequality accounting for the presence of a nontrivial right-hand side term, coupled with an higher integrability result of Gehring-type.
Lemma 2.3. Under assumptions (1.6)1,2,3, (1.7) and (1.10), let u∈W1,p(Ω,RN) be a local minimizer of functional (1.1).
● For every ball Bϱ(x0)⋐Ω and any u0∈RN, z0∈RN×n∖{0} it holds that
where E(⋅) is defined in (1.4), ℓ(x):=u0+⟨z0,x−x0⟩ and c≡c(n,N,λ,Λ,p).
● There exists an higher integrability exponent p2≡p2(n,N,λ,Λ,p)>p such that Du∈Lp2loc(Ω,RN×n) and the reverse Hölder inequality
is verified for all balls Bϱ(x0)⋐Ω with c≡c(n,N,λ,Λ,p).
Proof. For the ease of exposition, we split the proof in two steps, each of them corresponding to the proof of (2.7) and (2.8) respectively.
Step 1: proof of (2.7).
We choose parameters ϱ/2≤τ1<τ2≤ϱ, a cut-off function η∈C1c(Bτ2(x0)) such that 1Bτ1(x0)≤η≤1Bτ2(x0) and |Dη|≲(τ2−τ1)−1. Set φ1:=η(u−ℓ), φ2:=(1−η)(u−ℓ) and use (1.7) and the equivalence in (2.2)1 to estimate
where we have used the simple relation Dφ1+Dφ2=Du−z0. Terms I1 and I3 can be controlled as done in [19, Proposition 2]; indeed we have
for c≡c(n,N,λ,Λ,p). Concerning term I2, we exploit (1.10), the fact that φ1∈W1,p0(Bτ2(x0),RN) and apply Sobolev-Poincaré inequality to get
where c≡c(n,N,m) and we also used that ϱ/2≤τ2≤ϱ. Merging the content of the two above displays, recalling that η≡1 on Bτ1(x0) and choosing ε>0 sufficiently small, we obtain
with c≡c(n,N,λ,Λ,p). At this stage, the classical hole-filling technique, Lemma 2.2 and (2.3) yield (2.7) and the first bound in the statement is proven.
Step 2: proof of (2.8).
To show the validity of (2.8), we follow [33, proof of Proposition 3.2] and first observe that if u is a local minimizer of functional F(⋅) on Bϱ(x0), setting fϱ(x):=ϱf(x0+ϱx), the map uϱ(x):=ϱ−1u(x0+ϱx) is a local minimizer on B1(0) of an integral with the same integrand appearing in (1.1) satisfying (1.6)1,2,3 and fϱ replacing f. This means that (2.10) still holds for all balls Bσ/2(˜x)⊆Bτ1(˜x)⊂Bτ2(˜x)⊆Bσ(˜x)⋐B1(0), with ˜x∈B1(0) being any point, in particular it remains true if |z0|=0, while condition |z0|≠0 was needed only in the estimate of term I2 in (2.11), that now requires some change. So, in the definition of the affine map ℓ we choose z0=0, u0=(uϱ)Bσ(˜x) and rearrange estimates (2.10) and (2.11) as:
and, recalling that φ1∈W1,p0(Bτ2(˜x),RN), via Sobolev Poincaré, Hölder and Young inequalities and (1.11)2, we estimate
with c≡c(n,N,p). Plugging the content of the two previous displays in (2.9), reabsorbing terms and applying Lemma 2.2, we obtain
for c≡c(n,N,Λ,λ,p). Notice that
with equality holding when p<n, while for p≥n any value of p∗>1 will do. We then manipulate the second term on the right-hand side of (2.12) as
where we set
Plugging the content of the previous display in (2.12) and applying Sobolev-Poincaré inequality we get
with c≡c(n,N,Λ,λ,p). Now we can apply a variant of Gehring lemma [24, Corollary 6.1] to determine a higher integrability exponent s≡s(n,N,Λ,λ,p) such that 1<s≤m/(p∗)′ and
for c≡c(n,N,Λ,λ,p). Next, notice that
so plugging this last inequality in (2.14) and recalling that s(p∗)′≤m, we obtain
Setting p2:=sp>p above and recalling that ˜x∈B1(0) is arbitrary, we can fix ˜x=0, scale back to Bϱ(x0) and apply (2.1) to get (2.8) and the proof is complete. □
3.
Excess decay estimate
In this section we prove some excess decay estimates considering separately two cases: when a smallness condition on the excess functional of our local minimizer u is satisfied and when such an estimate does not hold true.
3.1. The nondegenerate scenario
We start working assuming that a suitable smallness condition on the excess functional E(u;Bϱ(x0)) is fulfilled. In particular, we prove the following proposition.
Proposition 3.1. Under assumptions (1.6)1,2,3, (1.7) and (1.10), let u∈W1,p(Ω,RN) be a local minimizer of functional (1.1). Then, for τ0∈(0,2−10), there exists ε0≡ε0(data,τ0)∈(0,1) and ε1≡ε1(data,τ0)∈(0,1) such that the following implications hold true.
● If the conditions
and
are verified on Bϱ(x0), then it holds that
for all β0∈(0,2/p), with c0≡c0(data)>0.
● If condition (3.1) holds true and
is satisfied on Bϱ(x0), then
for c0≡c0(data)>0.
Proof of Proposition 3.1. For the sake of readability, since all balls considered here are concentric to Bϱ(x0), we will omit denoting the center. Moreover, we will adopt the following notation (Du)Bς(x0)≡(Du)ς and, for all φ∈C∞c(Bϱ;RN), we will denote ‖Dφ‖L∞(Bϱ)≡‖Dφ‖∞. We spilt the proof in two steps.
Step 1: proof of (3.3).
With no loss of generality we can assume that E(u;Bϱ)>0, which clearly implies, thanks to (3.1), that |(Du)ϱ|>0.
We begin proving that condition (3.1) implies that
for a constant c≡c(p,ε0)>0. Indeed,
and (3.6) follows.
Consider now
and
Let us note that we have
Since |(Du)ϱ|>0 we have that the hypothesis of [12, Lemma 3.2] are satisfied with
Then,
Fix ε>0 and let δ≡δ(data,ε)>0 be the one given by [33, Lemma 2.4] and choose ε0 and ε1 sufficiently small such that
With this choice of ε0 and ε1 it follows that u0 is almost A-harmonic on Bϱ, in the sense that
with A as in (3.8). Hence, by [33, Lemma 2.4] we obtain that there exists h0∈W1,2(Bϱ;RN) which is A-harmonic, i.e.,
such that
and
We choose now τ0∈(0,2−10), which will be fixed later on, and estimate
where c≡c(data)>0 and where we have used the following property of A-harmonic functions
with γ>1 and c depending on n, N, and on the ellipticity constants of A.
Now, choosing
we have that this together with (3.9) gives that ε0≡ε0(data,τ0) and ε1≡ε1(data,τ0). Recalling the definition of u0 in (3.7) and (3.12) we eventually arrive at
for c≡c(data)>0. By a similar computation, always using (3.13), (3.10) and (3.11), we obtain that
In this way, as for (3.14), by the definition of u0 in (3.7), we eventually arrive at
with c≡c(data).
Denote now with ℓ2τ0ϱ the unique affine function such that
Hence, by (3.14) and (3.15), we conclude that
Notice that we have also used the property that
for p≥2, c≡c(n,N,p)>0 and for any affine function ℓ; see [33, Lemma 2.3].
Recalling the definition of the excess functional E(⋅), in (1.4), we can estimate the following quantity as follows
where we have used the following property of the affine function ℓ2τ0ϱ
for a constant c≡c(n,p)>0; see for example [33, Lemma 2.2].
Now, starting from (3.1) and (3.9), we further reduce the size of ε0 such that
where c≡c(n) is the same constant appearing in (3.17). Thus, combining (3.17) and (3.18), we get
The information provided by (3.18) combined with (3.16) allow us to conclude that
By triangular inequality and (3.19) we also get
which, therefore, implies that
where c≡c(data)>0. By triangular inequality, we can further estimate
where c≡c(p)>0. We now separately estimate the previous integrals. We begin considering I1. By Young and triangular inequalities we get
with c≡c(data)>0. In a similar fashion, we can treat the integral I2
where we have used the following property of the affine function ℓ2τ0ϱ
for a given constant c≡c(n,p)>0; see [33, Lemma 2.2]. Finally, the last integral I3 can be treated recalling (3.21) and (2.1), i.e.,
All in all, combining the previous estimate
up to choosing ε1 such that
Step 2: proof of (3.5).
The proof follows by [12, Lemma 2.4] which yields
Multiplying both sides by E(u;Bτ0ϱ)p−22 we get the desired estimate. □
3.2. The degenerate scenario
It remains to considering the case when condition (3.1) does not hold true. We start with two technical lemmas. The first one is an analogous of the Caccioppoli inequality (2.7), where we take in consideration the eventuality z0=0.
Lemma 3.1. Under assumptions (1.6)1,2,3, (1.7) and (1.10), let u∈W1,p(Ω,RN) be a local minimizer of functional (1.1). For every ball Bϱ(x0)⋐Ω and any u0∈RN, z0∈RN×n it holds that
where E(⋅) is defined in (1.4), ℓ(x):=u0+⟨z0,x−x0⟩ and c≡c(n,N,λ,Λ,p).
Proof. The proof is analogous to estimate (2.7), up to treating in a different way the term I2 in (2.9), taking in consideration the eventuality z0=0. Exploiting (1.10) and fact that φ1∈W1,p0(Bτ2(x0),RN), an application of the Sobolev-Poincaré inequality yields
where c≡c(n,N,m) and we also used that ϱ/2≤τ2≤ϱ. Hence, proceeding as in the proof of (2.7), we obtain that
with c≡c(n,N,λ,Λ,p). Concluding as in the proof of (2.7), we eventually arrive at (3.22). □ We will also need the following result.
Lemma 3.2. Under assumptions (1.6)1,2,3, (1.7) and (1.10), let u∈W1,p(Ω,RN) be a local minimizer of functional (1.1). For any Bϱ(x0)⋐Ω and any s∈(0,∞) it holds that
for any φ∈C∞0(Bϱ(x0),RN), with c≡c(n,N,Λ,λ,p).
Proof. Given the regularity properties of the integrand F, we have that a local minimizer u of (1.1) solves weakly the following integral identity (see [42, Lemma 7.3])
Now, fix φ∈C∞0(Bϱ(x0),RN) and split
We begin estimating the first integral I1. For s∈(0,∞) we get
On the other hand, the integral I2 can be estimated as follows
Combining the inequalities above we obtain (3.24). □
In this setting the analogous result of Proposition 3.1 is the following one.
Proposition 3.2. Under assumptions (1.6)1,2,3, (1.7) and (1.10), let u∈W1,p(Ω,RN) be a local minimizer of functional (1.1). Then, for any χ∈(0,1] and any τ1∈(0,2−10), there exists ε2≡ε2(data,χ,τ1)∈(0,1) such that if the smallness conditions
are satisfied on a ball Bϱ(x0)⊂Rn, then
for any β1∈(0,2α/p), with α≡α(n,N,p)∈(0,1) is the exponent in (3.34), and c1≡c1(data,χ).
Proof. We adopt the same notations used in the proof of Proposition 3.1. Let us begin noticing that condition (3.27)1 implies the following estimate
Indeed, by (1.4) and (3.27), we have
Consider now
for ε3∈(0,1], which will be fixed later on. Applying (3.24) to the function v0 yields
For any ε>0 and ϑ∈(0,1) and let δ be the one given by [17, Lemma 1.1]. Then, up to choosing s, ε2 and ε3 sufficiently small, we arrive at
Then, Lemma 1.1 in [17] implies
up to taking ε as small as needed. Now, denoting with h0:=hκ, we have that
Now, we choose ϑ:=(s)′/2, with s being the exponent given by (2.8). Note that by the proof of (2.8) it actually follows that ϑ<1. Thus, choosing εεp2κp≤τ2n+4α1 (where α∈(0,1) is given by (3.34)) we arrive at
By Hölder's Inequality, we have that
Hence, since by (2.3) V(z)≈|z|p, an application of estimates (2.8) and (3.29) now yields
with c≡c(data,χ).
On the other hand, by classical properties of p-harmonic functions, we have that
Hence, combining (3.30)–(3.32), we get that
Let us recall that, for any τ1∈(0,2−10), given the p-harmonic function h0 we have
Moreover, using Jensen's Inequality we can estimate the following difference as follows
Thus, up to taking ε2 sufficiently small, by the triangular inequality, we obtain that
Hence, (2.2) yield
and
Then,
and the desired estimate (3.28) follows. □
4.
Proof of the main result
This section is devoted to the proof of Theorem 1.1. First, we prove the following proposition.
Proposition 4.1. Under assumptions (1.6)1,2,3, (1.7) and (1.10), let u∈W1,p(Ω,RN) be a local minimizer of functional (1.1). Then, there exists ε∗≡ε∗(data)>0 such that if the following condition
is satisfied on Br⊂Ω, for some ε∈(0,ε∗], then
for c3≡c3(data)>0.
Proof. For the sake of readability, since all balls considered in the proof are concentric to Br(x0), we will omit denoting the center.
Let us start fixing an exponent β≡β(α,p) such that
where β0 and β1 are the exponents appearing in Propositions 3.1 and 3.2. Moreover, given the constant c0 and c1 from Propositions 3.1 and 3.2, choose τ≡τ(data,β) such that
With the choice of τ0 as in (4.4) above, we can determine the constant ε0 and ε1 of Proposition 3.1. Now, we proceed applying Proposition 3.2 taking χ≡ε0 and τ1 as in (4.4) there. This determines the constant ε2 and c2. We consider a ball Br⊂Ω such that
and
where the constant c2:=c1+c0, with c0 appearing in (3.5) and c1 in (3.28). In particular, see that by (4.5) and (4.6) we are in the case when (4.1) does hold true.
Now, we recall Proposition 3.2. Seeing that (3.27)2 is satisfied (being (4.5)) we only check whether (3.27)1 is verified too. If ε0|(Du)Br|≤E(Du;Br) is satisfied then we obtain from (3.28), with τ1≡τ in (4.4) that
where the last inequality follows from (4.5) and (4.6). If on the other hand it holds ε0|(Du)Br|≥E(Du;Br), by Proposition 3.1, then by (3.3) or (3.5) we eventually arrive at the same estimate (4.7).
Iterating now the seam argument we arrive at
and the estimate
holds true. By the inequality above we have that for any k≥0
Applying a standard interpolation argument we conclude that, for any t≤r, it holds
where c3≡c3(data). The desired estimate (4.2) now follows. □
Proof of Theorem 1.1. We proceed following the same argument used in [33, Theorem 1.5]. We star proving that, for any 1≤m<n and any O⊂Ω, with positive measure, we have that
Indeed, fix ˉλ which will be chosen later on. Then, we have that
The first integral on the righthand side of (4.10) can be estimated in the following way
On the other hand, the second integral can be estimated recalling the definition of the Ln,∞(O)-norm. Indeed,
Hence, putting all the estimates above in (4.10), choosing ˉλ:=‖f‖Ln,∞(O)/|O|1/n, we obtain (4.9).
Now, recalling condition (1.2) we have that
where ε∗ is the one obtained in the proof of Proposition 4.1. From this it follows that, we can choose a radius ϱ1 such that
We want to show that the set Ωu appearing in (1.3) can be characterized by
thus fixing ϱx0:=ϱ1 and εx0:=ε∗/(4c3). We first star noting that the the set Ωu defined in (1.4) is such that |ΩsetminusΩu|=0. Indeed, let us consider the set
which is such that |ΩsetminusLu|=0 by standard Lebesgue's Theory. Moreover, by (2.5) it follows that
so that, Lu⊂Ωu and we eventually obtained that |ΩsetminusΩu|=0. Now we show that Ωu is open. Let us fix x0∈Ωu and find a radius ϱx0≤ϱ1 such that
By absolute continuity of the functional E(⋅) we have that there exists an open neighbourhood O(x0) such that, for any x∈O(x0) it holds
This prove that Ωu is open. Now let us start noting that (4.11) and (4.14) yield that condition (4.1) is satisfied with Br≡Bϱx0(x). Hence, an application of Proposition 4.1 yields
for any x∈O(x0). Thus concluding the proof. □
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The author is supported by INdAM Projects "Fenomeni non locali in problemi locali", CUP_E55F22000270001 and "Problemi non locali: teoria cinetica e non uniforme ellitticità", CUP_E53C220019320001, and also by the Project "Local vs Nonlocal: mixed type operators and nonuniform ellipticity", CUP_D91B21005370003.
Conflict of interest
The author declares no conflict of interest.













 DownLoad:
DownLoad: