AIMS Mathematics, 2020, 5(4): 3762-3782. doi: 10.3934/math.2020244

Research article

Export file:

Format

  • RIS(for EndNote,Reference Manager,ProCite)
  • BibTex
  • Text

Content

  • Citation Only
  • Citation and Abstract

Positivity preserving interpolation by using rational quartic spline

Noor Adilla Harim, Samsul Ariffin Abdul Karim, Mahmod Othman, Azizan Saaban, Abdul Ghaffar, Kottakkaran Sooppy Nisar, Dumitru Baleanu

1 Fundamental and Applied Science Department, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 32610 Seri Iskandar, Perak DR, Malaysia
2 Fundamental and Applied Sciences Department and Centre for Smart Grid Energy Research (CSMER), Institute of Autonomous System, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 32610 Seri Iskandar, Perak DR
3 School of Quantitative Sciences, UUMCAS, Universiti Utara Malaysia, 06010 Sintok, Kedah, Malaysia
4 Informetrics Research Group, Ton Duc Thang University, Ho Chi Minh City 700000, Vietnam
5 Faculty of Mathematics & Statistics, Ton Duc Thang University, Ho Chi Minh City 700000, Vietnam
6 Department of Mathematics, College of Arts and Sciences, Wadi Aldawaser, 11991, Prince Sattam bin Abdulaziz University, Saudi Arabia
7 Department of Mathematics, Cankaya University, Ankara 06530, Turkey
8 Institute of Space Sciences, 077125 Magurele-Bucharest, Romania
9 Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, 40447, Taiwan

Received: , Accepted: , Published:

Abstract    Full Text(HTML)    Figure/Table    Related pages

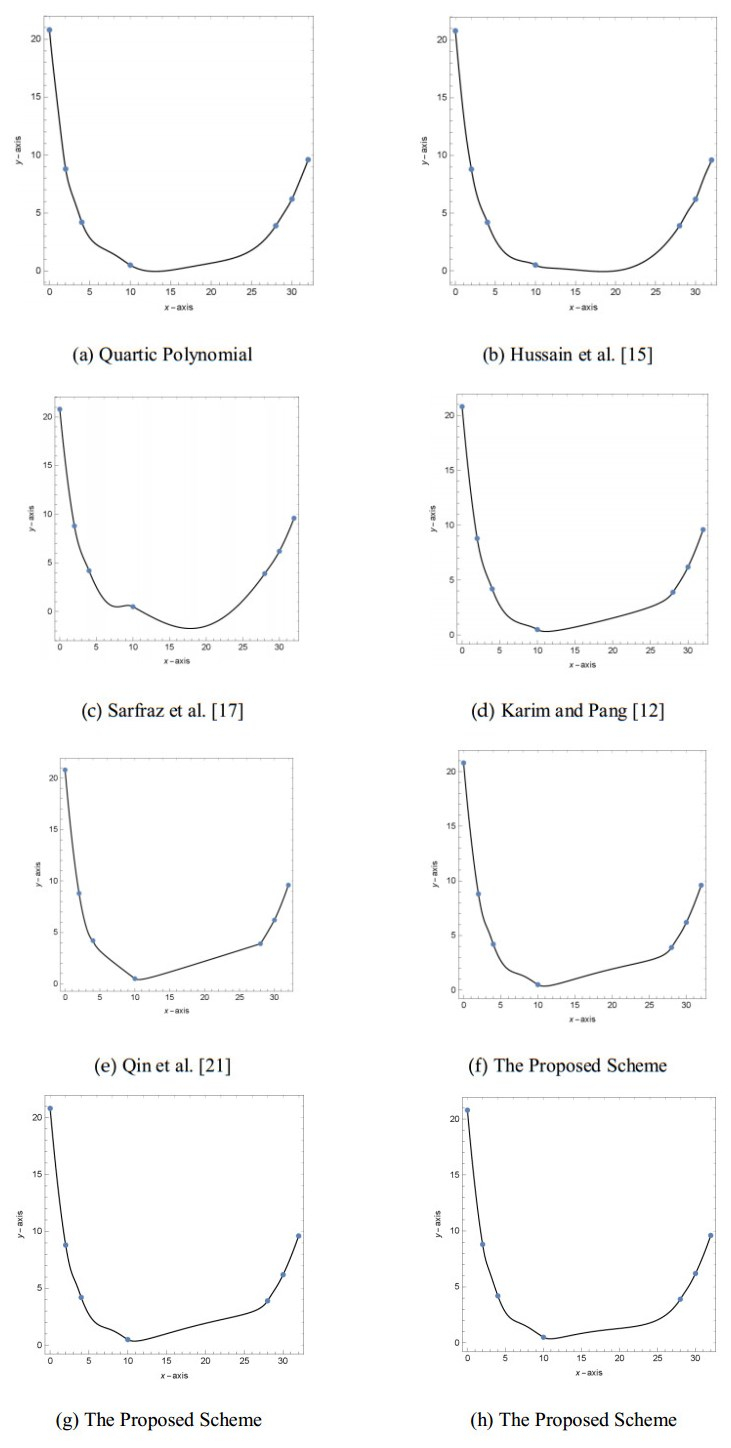
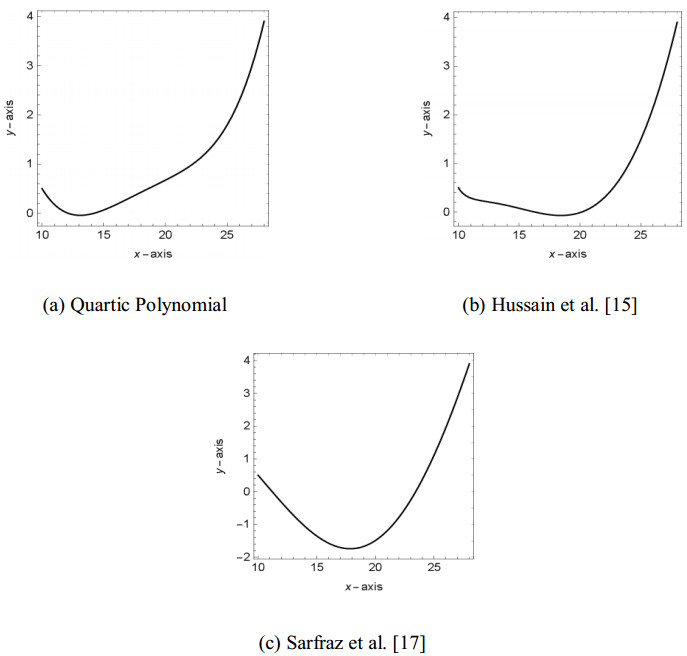
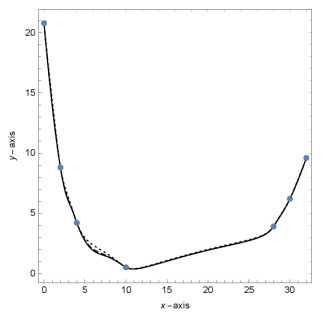
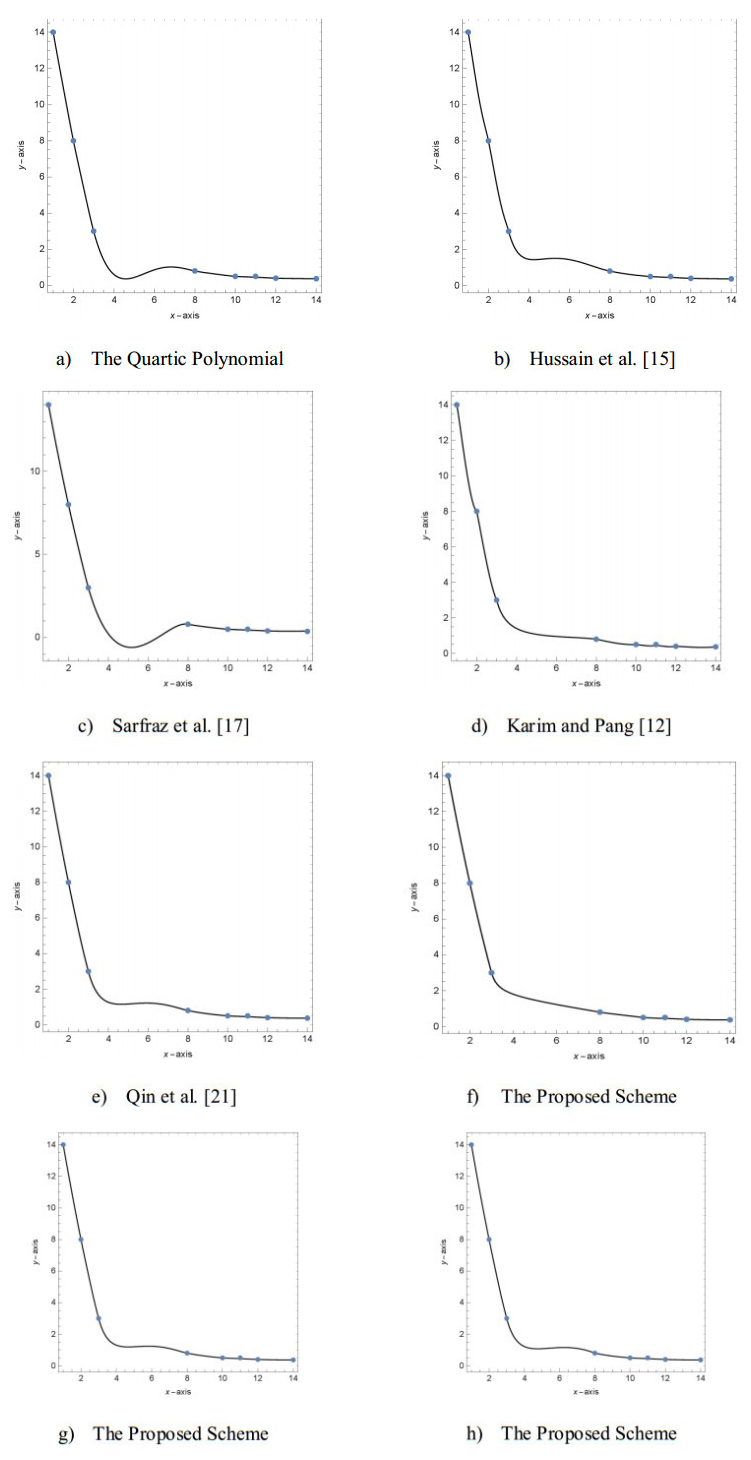
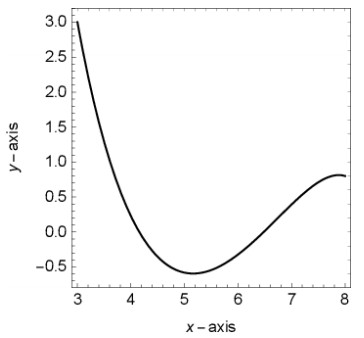
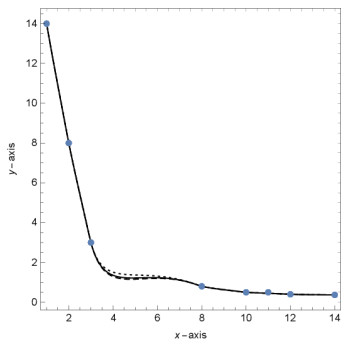
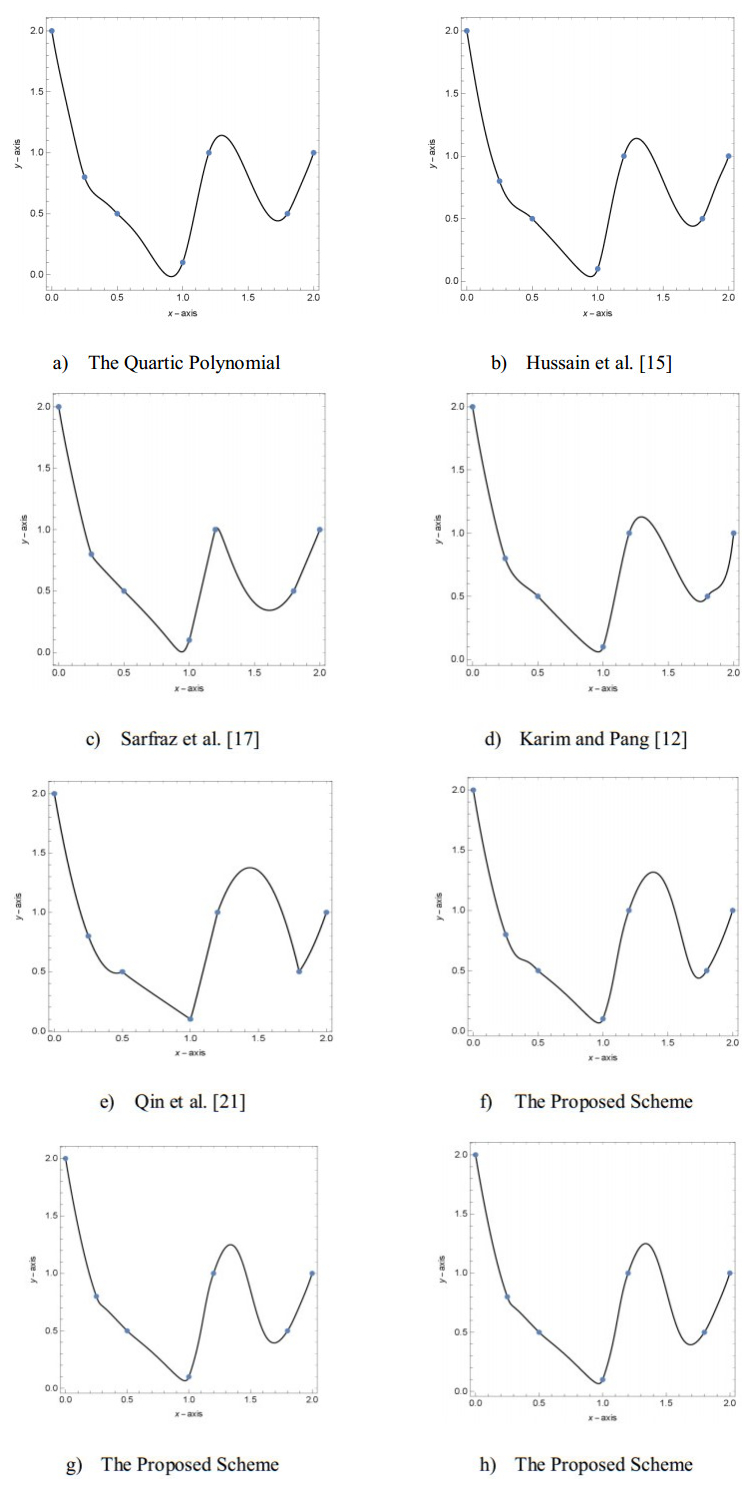
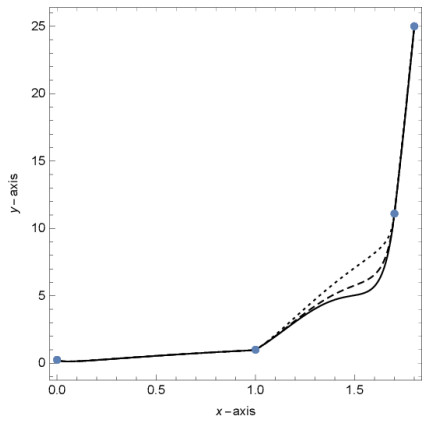
In this study, a new scheme for positivity preserving interpolation is proposed by using C1 rational quartic spline of (quartic/quadratic) with three parameters. The sufficient condition for the positivity rational quartic interpolant is derived on one parameter meanwhile the other two are free parameters for shape modification. These conditions will guarantee to provide positive interpolating curve everywhere. We tested the proposed positive preserving scheme with four positive data and compared the results with other established schemes. Based on the graphical and numerical results, we found that the proposed scheme is better than existing schemes, since it has extra free parameter to control the positive interpolating curve.
  Figure/Table
  Supplementary
  Article Metrics

References

1. M. R. Asim, K. W. Brodlie, Curve drawing subject to positivity and more general constraints, Comput. Graphics, 27 (2003), 469-485.    

2. T. N. T. Goodman, Shape preserving interpolation by curves, Proceeding of Algorithms for approximation IV, J. Levesley, I. J. Anderson, J. C. Mason,Eds., University of Huddersfield, Huddersfield, UK, 2002, 24-35.

3. M. Sarfraz, A rational cubic spline for the visualization of monotonic data, Comput. Graphics, 24 (2000), 509-516.    

4. M. Sarfraz, Visualization of positive and convex data by a rational cubic spline interpolation, Infor. Sci., 146 (2002), 239-254.

5. R. Delbourgo, J. A. Gregory, Shape preserving piecewise rational interpolation, SIAM J Sci. Stat. Comput., 6 (1985), 967-976.    

6. K. W. Brodlie, S. Butt, Preserving convexity using piecewise cubic interpolation, Comput. Graphics, 15 (1991), 15-23.    

7. K. W. Brodlie, P. Mashwama, S. Butt, Visualization of surface data to preserve positivity and other simple constraints. Comput. Graphics, 19 (1995), 585-594.

8. M. Sarfraz, M. Z. Hussain, M. Hussain, Shape-preserving curve interpolation, Int. J. Comput. Math., 89 (2012), 35-53.    

9. X. Peng, Z. Li, Q. Sun, Nonnegativity preserving interpolation by C1 Bivariate Rational Spline Surface. J. Appl. Math., 624978 (2010), 11.

10. E. S. Chan, V. P. Kong, B. H. Ong, Constrained C1 interpolation on rectangular grids, In: Computer Graphics, Imaging and Visualization, 2004, CGIV 2004, Proceedings, International Conference on (239-244), IEEE.

11. S. Butt, K. W. Brodlie, Preserving positivity using piecewise cubic interpolation, Comput. Graphics, 17 (1993), 55-64.

12. S. A. A. Karim, V. P. Kong, Shape Preserving Interpolation Using C2 Rational Cubic Spline, J. Appl. Math., Article ID 4875358, 2016.

13. S. A. A. Karim, A. Saaban, Shape Preserving Interpolation Using Rational Cubic Ball Function and Its Application in Image Interpolation, Math. Probl. Eng., Article ID 7459218, 2017.

14. S. A. A. Karim, V. P. Kong, Shape preserving interpolation using rational cubic spline, Res. J. Appl. Sci., Eng. Technol., 8 (2014), 167-178.    

15. M. Z. Hussain, M. Hussain, S. Samreen, Visualization of shaped data by rational quartic spline interpolation, Int. J. Appl. Math. Stat., 13 (2008), 34-46.

16. Q. Wang, J. Tan, Rational quartic spline involving shape parameter, J. Infor. Comput. Sci., 1 (2004), 127-130.

17. M. Sarfraz, M. Z. Hussain, A. Nisar, Positive data modeling using spline function, Appl. Math. Comput., 216 (2010), 2036-2049.

18. A. Harim, S. A. A. Karim, M. Othman, et al. High Accuracy Data Interpolation using Rational Quartic Spline with Three parameters, Int. J. Sci. Technol. Res., 2019, 1219-27432.

19. R. Delbourgo, Shape preserving interpolation to convex data by rational functions with quadratic numerator and linear denominator, IMA J. Numer. Anal., 9 (1989), 123-136.    

20. R. Delbourgo, J. A. Gregory, The determination of derivative parameters for a monotonic rational quadratic interpolant, IMA J. Numer. Anal., 5 (1985), 397-406.

21. X. Qin, L. Qin, Q. Xu, C1 positivity-preserving interpolation schemes with local free parameters, IAENG Int. J. Comput. Sci., 43 (2016).

22. M. Z. Hussain, J. Ali, Positivity-preserving piecewise rational cubic interpolation, MATEMATIKA: Malaysian J. Ind. Appl. Math., 22 (2006), 147-153.

23. J. Wu, X. Zhang, L. Peng, Positive approximation and interpolation using compactly supported radial basis functions, Math. Probl. Eng., Article ID 964528, 2010.

24. M. Z. Hussain, M. Sarfraz, M. T. S. Shaikh, Shape preserving rational cubic spline for positive and convex data, Egyptian Infor. J., 12 (2011), 231-236.

25. Y. Zhu, C2 positivity-preserving rational interpolation splines in one and two dimensions, Appl. Math. Comput., 316 (2018), 186-204.

26. Y. Zhu, C2 Rational Quartic/Cubic Spline Interpolant with Shape Constraints, Results Math., 73 (2018), 127.

© 2020 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution Licese (http://creativecommons.org/licenses/by/4.0)

Download full text in PDF

Export Citation

Article outline

Show full outline
Copyright © AIMS Press All Rights Reserved