Normalization proofs for the un-typed μμ-calculus

1.   Introduction

Solving completely integrable models is very important for observing and meaning dynamical behaviors of the physical systems. The shallow water wave model is one of the completely integrable models illustrating many physical problems. Euler is the first derived the water wave model in the 18th century. Using many models in applied mathematics and in physics such as Boussinesq equations, KdV equation, Davey–Stewarts on equation, Kadomtsev–Petviashvili (KP) equation, Benjamin–Bona–Mahony (BBM) equation are derived by Euler equations. The Benney–Luke equation is also water wave approximation to the Euler equation.

The KdV equation and the Benjamin–Bona–Mahony describe water waves that travel mainly in one direction. The Benney–Luke equation allows two-directional approximation to the Euler equations ^[1,2]. The KP equation is the 2D general form of KdV equation. It describes long wavelength water waves in a weak dispersion medium. The Benjamin–Bona–Mahony (BBM) equation is also known regularized long-wave equation is an improvement form of KdV equation. It is derived to model long waves propagation in nonlinear dispersion. The KP equation and the BBM equations are used to symbolize for acoustic waves in fluids, long wavelength surface wave in liquids.

In this study we consider the combined the two equations which is KP-BBM equation given as ^[3];

where $a, b, k$ are constants and non-zero.

Many scientists have investigated the KP-BBM equation via various methods. In ^[4], the bifurcation of solitary waves of Eq. (1) is studied. The (3+1)-dimensional KP-BBM equation has been extracted to find analytical solutions by the auxiliary equation method ^[5]. Trigonometric and hyperbolic function solutions have been presented by new generalized (G′/G) expansion method ^[6]. The bell-shaped solitary wave and periodic wave solutions of KP-BBM equation have been obtained by bifurcation method and analyzed relation between of solutions under the different conditions ^[7]. The KP-BBM equation has been turned into Hirota bilinear form and obtained lump solutions by this way. The authors have investigated interactions lump-kink solutions and lump-soliton solutions ^[8].

In this work, we consider the Benney-Luke equation, the other model is derived from 3-dimensional Euler’s equation.

The Benney-Luke equation is given by ^[9,10]

where are arbitrary constants such that, is the Bond number capturing the effects of surface tension and gravity forces. Eq. (2) models an approximation of the full water wave equation and is formally suitable to describe the two way propagation of water waves in the presence of surface tension. Firstly, Eq. (2) is presented by Benney and Luke ^[11]. There are comprehensive studies such as numerical studies, stability analysis, traveling wave solutions, analytical solutions, Cauchy problem on this equation in the literature ^{[1,9,10,11,12,13,14,15]}.

The shallow water wave equations used in geophysical fluid dynamics, oceanography, coastal engineering and atmospheric science. Especially, in the past fifty years, solitary waves and soliton solutions have been intensively studied in mathematical, physical and engineering fields. Some powerful methods are recommended to find solitary wave solutions such as Hirota’s method ^[16], inverse scattering transform method ^[17], the solitary wave ansatz method ^[18,19], the tanh method ^[20], the extended auxiliary equation mapping, the extended direct algebraic mapping methods ^{[21,22,23,24,25,26,27,28,29,30,31,32,33]}, Riemann–Hilbert method ^[34,35], the Lie symmetry method ^[36,37], and many others ^{[38,39,40,41,42,43]}.

In this study, we focus on the sine-Gordon expansion method to construct to exact solutions of the KP-BBM equation and the Benney–Luke equation.

This paper rested as, the general properties of the mentioned method are given in Section 2. To obtain the soliton solutions the SGEM is applied to Eqs. (1) and (2), then 2D, 3D and contour simulations of the new solutions are plotted in Section 3. Finally, we give conclusion by submitted findings.

2.   The sine-Gordon expansion method

In this section, we describe SGEM. Firstly, we need to explain how we get two significant equations. We suppose that the sine-Gordon equation is given as following ^{[44,45,46,47]};

Where $u = u(x, t)$, $m$is a real constant. Applying the wave transform $u = u(x, t) = U(\xi ),$$\xi = x - ct$to Eq. (3), we get the following nonlinear ordinary differential equation;

Where $U = U(\xi ), \xi$ and $c$are the amplitude and velocity of the travelling waves, respectively. We integrate Eq. (4) and it can be written as follows;

Where $K$ is the constant of integration. Substituting $K = 0, w\left( \xi \right) = \frac{U}{2}$ and ${a^2} = \frac{{{m^2}}}{{\left( {1 - {c^2}} \right)}}$in Eq. (5), it yields;

Setting $a = 1$ in Eq. (6), gives;

Solving Eq. (7) by variables separable, we obtain the two significant equations as;

Where $p$ is the integral constant and non-zero.

We suppose that the general nonlinear partial differential equation of the following form;

where $u = u(x, t)$. We consider the solution of Eq. (10) as following expression,

Eq. (11) can be rearranged according to Eq. (8) and Eq. (9) as follows;

Using the homogenous balance principle to determine the value of$n$between the highest power nonlinear term and highest derivative in the ordinary differential equation. We suppose that the summation of coefficients of ${\sin ^i}\left( w \right){\cos ^j}\left( w \right)$ with the same power is zero, this yields an equation system. With aid of the computational program, we solve the equation system to find the values of ${A_i}, {B_i}, \mu {\rm{ and }}c.$Finally, substituting the values of ${A_i}, {B_i}, \mu {\rm{ and }}c$into Eq. (11), we get the new travelling wave solutions to the Eq. (10).

3.   Applications of the method

In this section, we will present the application of the SGEM to the KP-BBM and the Benney–Luke equations.

3.2.   The KP-BBM equation

Let consider the following wave transform as,

Using above transformation into Eq. (1), we get the following ordinary differential equation by integrating twice with respect to $\zeta$,

We choose the integration constant to be zero. Balancing between $U''$ and ${U^2}$gives $n = 2$.

For the value $n = 2$, the Eq. (12) takes the form,

Differentiating Eq. (15) twice, yields

Substituting Eq. (15) and Eq. (16) into Eq. (14), we have a polynomial in term of trigonometric functions. Equating to zero all sum of coefficients of the same power of the trigonometric functions, we get the following algebraic equation system. Putting the values of the coefficients into Eq. (15), we obtain the following cases.

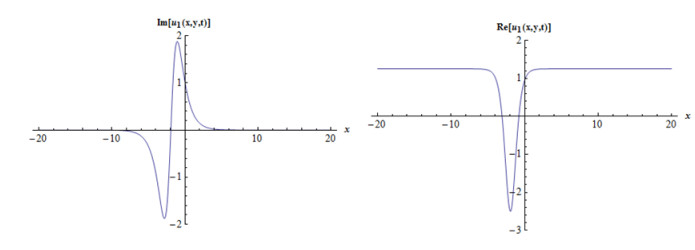
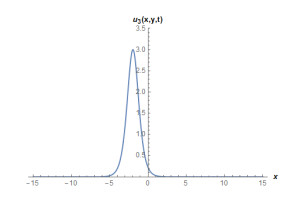
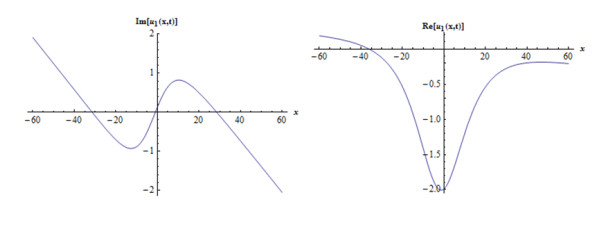
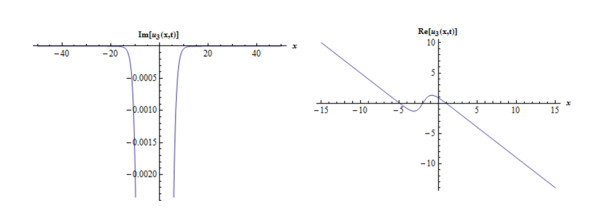
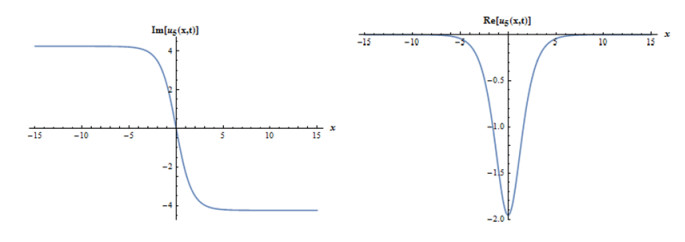
Case 1: When we consider as ${A_0} = - \frac{{2b(1 + k)}}{{a(1 + b)}}, {A_2} = \frac{{3b(1 + k)}}{{a(1 + b)}}, {B_2} = \frac{{3ib(1 + k)}}{{a(1 + b)}},$ $c = \frac{{1 + k}}{{1 + b}}, {A_1} = {B_1} = 0,$ gives following complex mixed dark-bright soliton solution,

where $f\left( {x, y, t} \right) = \frac{{(1 + k)t}}{{1 + b}} - x - y$. Considering suitable values of parameters, various figures may be observed as in Figures 1 and 2.

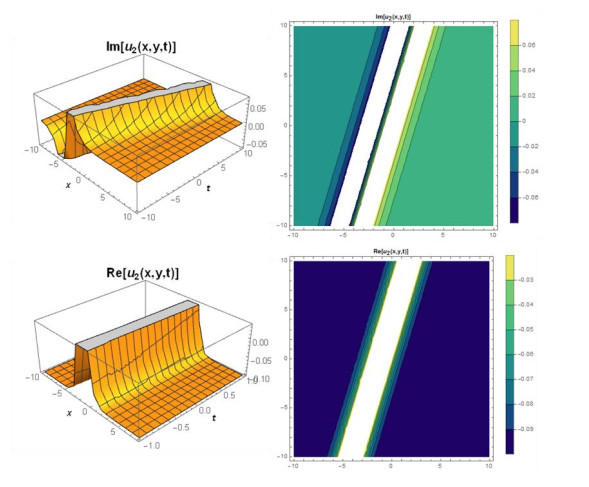
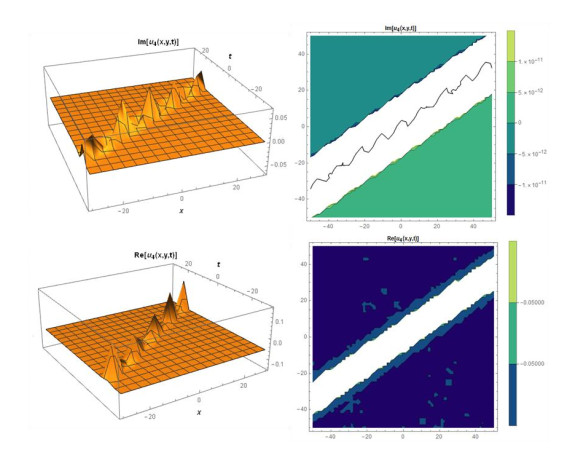
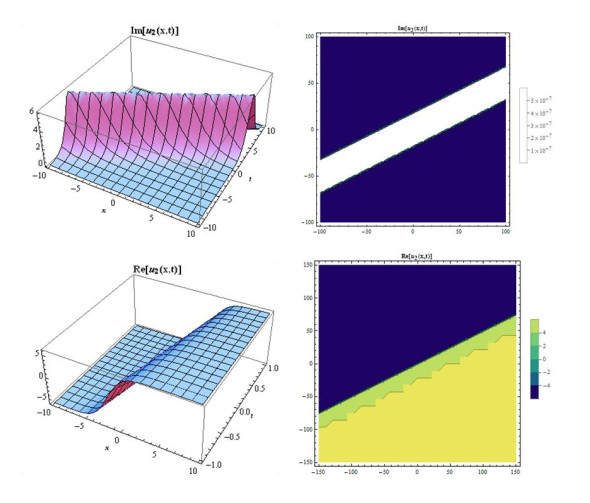
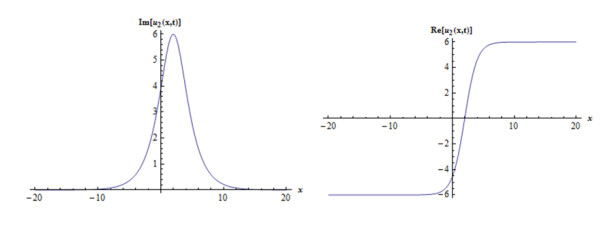
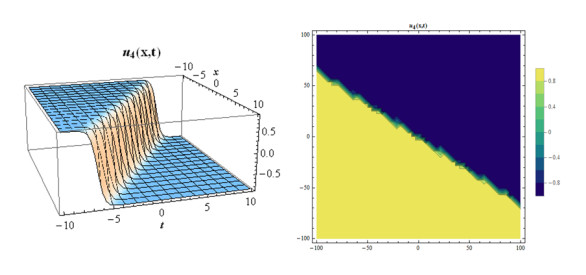
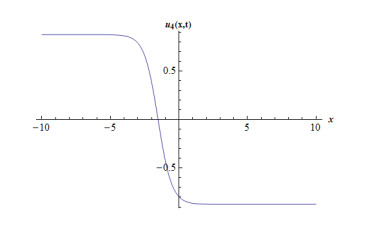
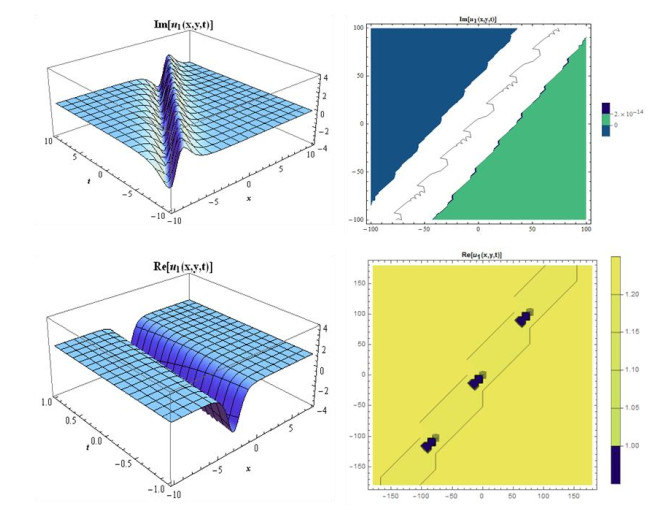
Case 2: When we take coefficients as, ${A_2} = - \frac{{3{A_0}}}{2}, {B_2} = \frac{{3i{A_0}}}{2}, b = - \frac{{a{A_0}}}{{2c}}, k = - 1 + c - \frac{{a{A_0}}}{2}, {A_1} = {B_1} = 0,$gives the following,

Considering suitable values of parameters, various figures may be observed as in Figures 3 and 4.

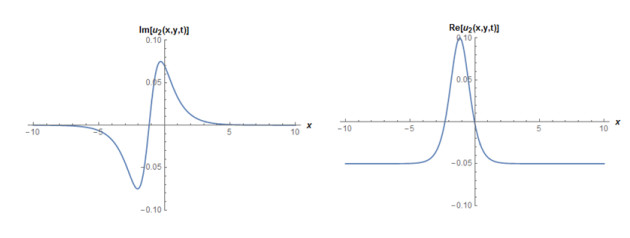
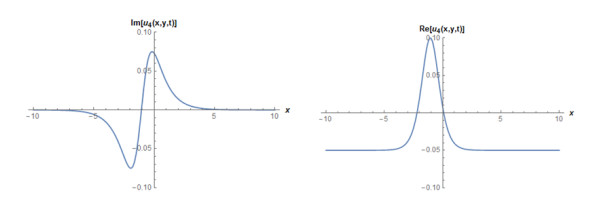
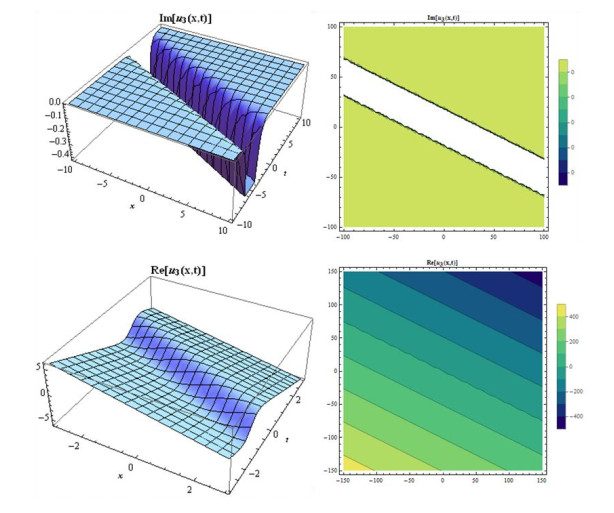
Case 3: If ${A_2} = - {A_0}, b = \frac{{a{A_0}}}{{ - 6\left( {1 + k} \right) + 4a{A_0}}}, c = 1 + k - \frac{{2a{A_0}}}{3}, {A_1} = {B_1} = {B_2} = 0,$enable to write the solution as,

We consider suitable values of parameters at above solution, then some figures may be observed as in Figures 5 and 6.

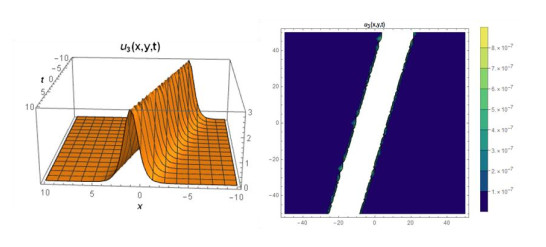
Case 4: Considering aswe find the

We found various figures for suitable values of parameters as Figures 7 and 8,

3.2.   The Benney-Luke equation

Let consider the following wave transform as,

Using above transformation into Eq. (2), we get the following nonlinear ordinary differential equation,

Integrating Eq. (22) with respect to $\zeta$once, we find,

After getting transform $V' = U$, we can write as

We choose the integration constant to be zero. Balancing between $U''$ and ${U^2}$ gives $n = 2$.

Substituting Eq. (15) and Eq. (16) into Eq. (24), we have a polynomial in term of trigonometric functions.

Equating to zero all sum of coefficients of the same power of the trigonometric functions, we get the following algebraic equation system. Putting the values of the coefficients into Eq. (15), we obtain the following cases.

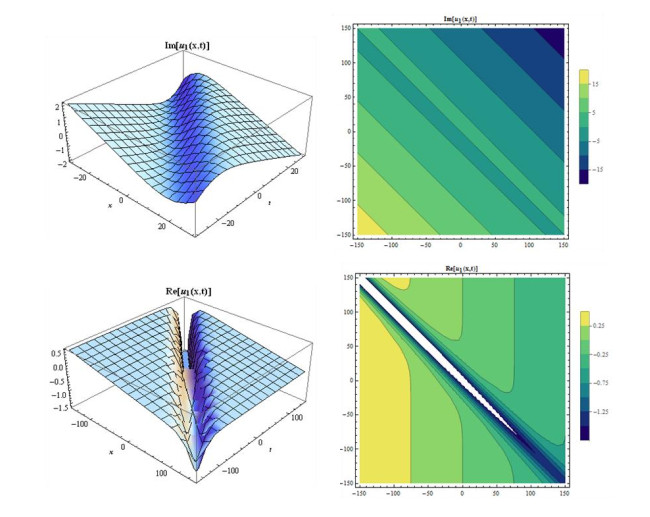
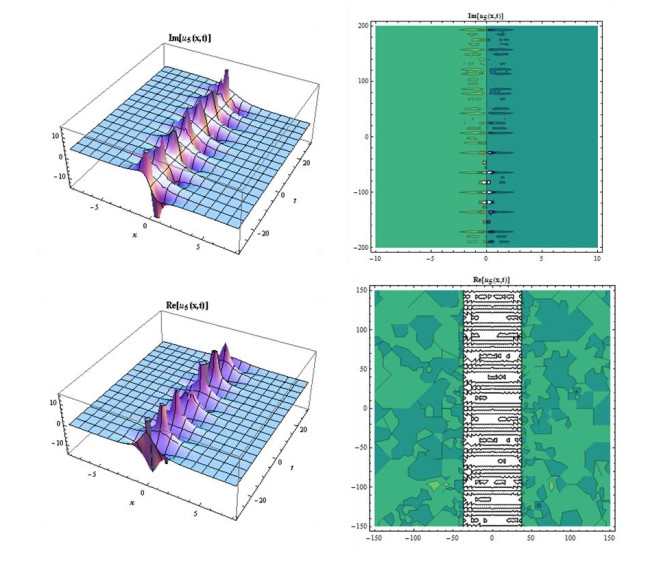
Case 1: When we consider ${A_0}{\rm{ }} = - \frac{{2i{B_2}}}{3}, {A_2} = i{B_2}, \beta = - \frac{1}{2}i\left( {\frac{{{B_2}}}{c} + \frac{{4\alpha }}{{ - 2i + {B_2}c}}} \right), k = - \frac{{\left( {1 + i} \right)c}}{{\sqrt {2i - {B_2}c} }}, {A_1} = {B_1} = 0,$gives the following complex mixed dark-bright soliton solution,

We consider suitable values of parameters to Eq. (25), then some figures may be observed as in Figures 9 and 10.

Case 2: If we take following coefficients, ${A_0}{\rm{ }} = \frac{{{c^2} - {k^2} + 5\left| {{c^2} - {k^2}} \right|}}{{3c{k^2}}}, {A_2}{\rm{ }} = - \frac{{2\left| {{c^2} - {k^2}} \right|}}{{c{k^2}}}, {B_2} = \frac{{2i}}{c} - \frac{{2ic}}{{{k^2}}}, \alpha = \frac{{ - \left| {{c^2} - {k^2}} \right| + {c^2}{k^2}\beta }}{{{k^4}}}, {A_1} = {B_1} = 0,$enable to write the solution as,

We consider suitable values of parameters at above solution, then some figures may be observed as in Figures 11 and 12.

Case 3: When the coefficients are taken as, ${A_0}{\rm{ }} = - \frac{{2{A_2}}}{3}, {B_2} = i{A_2}{\rm{, }}\alpha {\rm{ = }}\frac{{\left( {2 + {A_2}c} \right)\left( {{A_2} + 2c\beta } \right)}}{{4c}}, k = - c\sqrt {\frac{2}{{2 + {A_2}c}}} , {A_1} = {B_1} = 0,$we find another dark soliton solution,

Taking suitable values of parameters, various figures may be observed as in Figures 13 and 14.

Case 4: When we consider following coefficients,

gives the following,

We found various figures for suitable values of parameters as above Figures 15 and 16.

Case 5:${A_0}{\rm{ }} = \frac{{\sqrt 2 \left( {\alpha - \beta } \right)}}{{\sqrt { - \alpha - \beta } }}, {A_2} = \frac{{\sqrt 2 \left( { - \alpha + \beta } \right)}}{{\sqrt { - \alpha - \beta } }}, {B_2} = \sqrt {\frac{{2{{\left( {\alpha - \beta } \right)}^2}}}{{\alpha + \beta }}} , c = \frac{{\sqrt { - \alpha - \beta } }}{{\sqrt 2 \beta }}, k = \frac{i}{\beta }, {A_1} = {B_1} = 0,$gives us,

Taking suitable values of parameters in Eq. (29), we found some simulations as in Figures 17 and 18.

4.   Results and discussion

We would like to thank you for following the instructions above very closely in advance. It will definitely save us lot of time and expedite the process of your paper's publication.

We consider the sine-Gordon expansion method which is based on sine-Gordon equation to construct new type solution to Eq. (1) and Eq. (2). In the literature, there have been many techniques submitted such as Lie symmetry analysis, extended auxiliary equation mapping, extended direct algebraic mapping method, Hirota bilinear method, reductive perturbation technique. Kink, anti-kink solutions, lump solutions, line soliton, periodic waves and others have been shown by these mathematical tools. When we compare our results with other solutions, one can see that complex structure of obtained solutions are the feature that distinguishes it from others. Complex dark soliton, complex bright soliton solutions have more general structure than obtained by other techniques. In physics, complex calculus is considered to be of a formal mathematical, auxiliary type. Physical quantities can currently be defined by negative as well as by irrational number. Complex quantities extend some concepts as stability, convergence, conservation laws to reality. Consequently, complex-valued solutions can be verified in the experimental tests by physicist and engineers.

Complex numbers are particularly useful in explaining wave propagation. It is much easier to deal with the wave equation if we consider complex solutions. Since complex representation makes it much simpler to manage wave super-positions. If the refractive index of wave is enabled to be complex, the wave equation can be used to explain wave amplification and wave attenuation. In physical meaning, amplified waves are the fundamental basis for lasers when attenuated waves explain the absorption of light into black surfaces or the dissipation of sound into ambient heat ^[48].

Therefore, it is estimated that the results found in this paper may be used to explain such relationship of the governing models.

5.   Conclusion

In this work, we have successfully performed SGEM to construct new complex combined dark-bright soliton solutions of the KP-BBM and the Benney–Luke equation. We have obtained many new soliton solutions. We observed that providing all solutions the mentioned two nonlinear partial differential equations by using a software. When we compare the SGEM with other analytical methods such as the extended tanh method, the new generalized (G′/G)-expansion method, the auxiliary equation method, we can deduce that this method is very effective and powerful tool for nonlinear models. To the best of our knowledge, these new complex combined dark-bright soliton solutions have been firstly submitted to the literature. It may be observed that wave behavior have shown their estimated wave propagations and distributions, physically, in Figures 1–18. Moreover, the submitted solutions may be helpful understanding physical phenomena especially in oceanography, geophysical science. The results show that the proposed method can be efficiently used to such completely integrable equations.

Conflict of interest

The authors declare no conflict of interest.