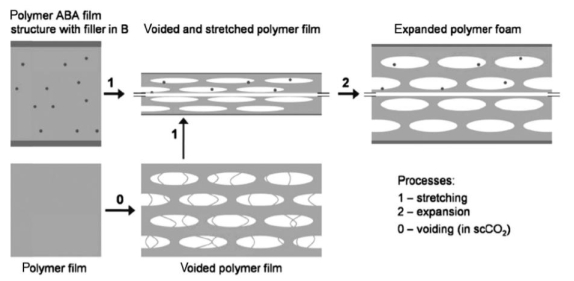
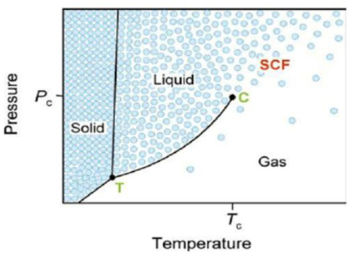
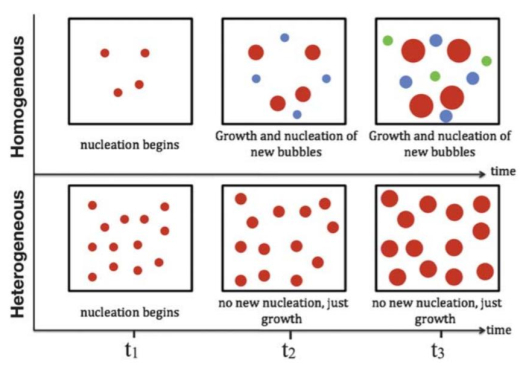
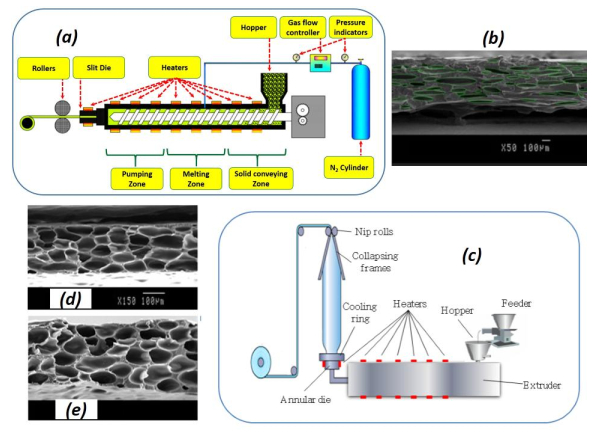
|
[1]
|
Dagdeviren C, Joe P, Tuzman OL, et al. (2016) Recent progress in flexible and stretchable piezoelectric devices for mechanical energy harvesting, sensing and actuation. Extreme Mech Lett 9: 269–281. doi: 10.1016/j.eml.2016.05.015

|
|
[2]
|
Mohebbi A, Mighri F, Ajji A, et al. (2018) Cellular polymer ferroelectret: A review on their development and their piezoelectric properties. Adv Polym Tech 37: 468–483. doi: 10.1002/adv.21686

|
|
[3]
|
Harrison JS, Ounaies Z (2002) Piezoelectric polymers, In: Encyclopedia of Polymer Science and Technology, 474–498.
|
|
[4]
|
Mohebbi A, Mighri F, Ajji A, et al. (2015) Current issues and challenges in polypropylene foaming: A review. Cell Polym 34: 299–337.
|
|
[5]
|
Hamdi O, Mighri F, Rodrigue D (2018) Optimization of the cellular morphology of biaxially stretched thin polyethylene foams produced by extrusion film blowing. Cell Polym [In press].
|
|
[6]
|
Zhai W, Wang H, Yu J, et al. (2008) Cell coalescence suppressed by crosslinking structure in polypropylene microcellular foaming. Polym Eng Sci 48: 1312–1321. doi: 10.1002/pen.21095

|
|
[7]
|
Rachtanapun P, Selke SEM, Matuana LM (2004) Effect of the high‐density polyethylene melt index on the microcellular foaming of high‐density polyethylene/polypropylene blends. J Appl Polym Sci 93: 364–371. doi: 10.1002/app.20428

|
|
[8]
|
Rachtanapun P, Selke SEM, Matuana LM (2004) Relationship between cell morphology and impact strength of microcellular foamed high‐density polyethylene/polypropylene blends. Polym Eng Sci 44: 1551–1560. doi: 10.1002/pen.20152

|
|
[9]
|
Huang HX (2005) HDPE/PA-6 blends: Influence of screw shear intensity and HDPE melt viscosity on phase morphology development. J Mater Sci 40: 1777–1779. doi: 10.1007/s10853-005-0692-x

|
|
[10]
|
Huang HX, Jiang G, Mao SQ (2005) Effect of flow fields on morphology of PP/Nano/CaCO3 composite and its rheological behavior. ASME International Mechanical Engineering Congress and Exposition,Orlando, Florida, USA, 80830: 567–574.
|
|
[11]
|
Huang HX, Wang JK, Sun XH (2008) Improving of cell structure of microcellular foams based on polypropylene/high-density polyethylene blends. J Cell Plast 44: 69–85. doi: 10.1177/0021955X07086082

|
|
[12]
|
Ding J, Shangguan J, Ma W, et al. (2013) Foaming behavior of microcellular foam polypropylene/modified nano calcium carbonate composites. J Appl Polym Sci 128: 3639–3651.
|
|
[13]
|
Wang C, Ying S, Xiao Z (2013) Preparation of short carbon fiber/polypropylene fine-celled foams in supercritical CO2. J Cell Plast 49: 65–82. doi: 10.1177/0021955X12459642

|
|
[14]
|
Zheng WG, Lee YH, Park CB (2010) Use of nanoparticles for improving the foaming behaviors of linear PP. J Appl Polym Sci 117: 2972–2979.
|
|
[15]
|
Mohebbi A, Mighri F, Ajji A, et al. (2017) Effect of processing conditions on the cellular morphology of polypropylene foamed films for piezoelectric applications. Cell Polym 36: 13–34.
|
|
[16]
|
Audet E (2015) Films cellulaires en polypropylène chargé de talc et de carbonate de calcium utilisés comme matériaux piézoélectriques: optimisation de la structure cellulaire par étirage bi-axial et par gonflement sous atmosphère d'azote [Thesis]. Laval University.
|
|
[17]
|
Wegener M, Wirges W, Fohlmeister J, et al. (2004) Two-step inflation of cellular polypropylene films: void-thickness increase and enhanced electromechanical properties. J Phys D Appl Phys 37: 623–627. doi: 10.1088/0022-3727/37/4/013

|
|
[18]
|
Sborikas M, Wegener M (2013) Cellular-foam polypropylene ferroelectrets with increased film thickness and reduced resonance frequency. Appl Phys Lett 103: 252901.
|
|
[19]
|
Qiu X, Xia Z, Wang F (2007) Piezoelectricity of single-and multi-layer cellular polypropylene film electrets. Front Mater Sci China 1: 72–75. doi: 10.1007/s11706-007-0013-1

|
|
[20]
|
Rychkova D, Altafim RAP, Qiu X, et al. (2012) Treatment with orthophosphoric acid enhances the thermal stability of the piezoelectricity in low-density polyethylene ferroelectrets. J Appl Phys 111: 124105.
|
|
[21]
|
An Z, Zhao M, Yao J, et al. (2009) Improved piezoelectric properties of cellular polypropylene ferroelectrets by chemical modification. Appl Phys A-Mater 95: 801–806.
|
|
[22]
|
Padasalkar GG, Shaikh JM, Syed YD, et al. (2015) A Review on Piezoelectricity. IJAREEIE 4: 8231–8235.
|
|
[23]
|
Pandey A, Shukla S, Shukla V (2015) Innovation and application of piezoelectric materials: a theoretical approach. IJATES 3: 1413–1417.
|
|
[24]
|
Li W, Torres D, Diaz R, et al. (2017) Nanogenerator-based dual-functional and self-powered thin patch loudspeaker or microphone for flexible electronics. Nat Commun 8: 15310.
|
|
[25]
|
Curie J, Curie P (1880) Development by pressure of polar electricity in hemihedral crystals with inclined faces. Bull Soc Min de France 3: 90–93.
|
|
[26]
|
Defay E (2013) Dielectricity, Piezoelectricity, Pyroelectricity and Ferroelectricity, In: Defay E, Integration of Ferroelectric and Piezoelectric Thin Films: Concepts and Applications for Microsystems, Great Britain and United States: ISTE Ltd and John Wiley & Sons, Inc., 1–24.
|
|
[27]
|
Setter N, Damjanovic D, Eng L, et al. (2006) Ferroelectric thin films: Review of materials, properties, and applications. J Appl Phys 100: 051606. doi: 10.1063/1.2336999

|
|
[28]
|
Abraham CS (2011) A review of ferroelectric materials and their applications. Ferroelectrics 138: 307–309.
|
|
[29]
|
Graz I, Mellinger A (2016) Polymer Electrets and Ferroelectrets as EAPs: Fundamentals, In: Carpi F, Electromechanically Active Polymers. Polymers and Polymeric Composites: A Reference Series, Springer, Cham.
|
|
[30]
|
Kirjavainen K (1987) Electromechanical film and procedure for manufacturing same. U.S. Patent, No: 4654546.
|
|
[31]
|
Savolainen A, Kirjavainen K (1989) Electrothermomechanical film. Part I. Design and characteristics. J Macromol Sci A 26: 583–591.
|
|
[32]
|
Rychkov D, Altafim RAP (2016) Polymer Electrets and Ferroelectrets as EAPs: Models, In: Carpi F, Electromechanically Active Polymers. Polymers and Polymeric Composites: A Reference Series, Springer, Cham.
|
|
[33]
|
Hillenbrand J, Sessler G, Zhang X (2005) Verification of a model for the piezoelectric d33 coefficient of cellular electret films. J Appl Phys 98: 0641051.
|
|
[34]
|
Sessler GM, Hillenbrand J (1999) Electromechanical response of cellular electrets films. Appl Phys Lett 75: 3405–3407. doi: 10.1063/1.125308

|
|
[35]
|
Zhanh H (2010) Scale-up of extrusion foaming process for manufacture of polystyrene foams using carbon dioxide [Thesis]. University of Toronto.
|
|
[36]
|
Wegener M (2010) Piezoelectric polymer foams: transducer mechanism and preparation as well as touch-sensor and ultrasonic-transducer properties. Proceedings Volume 7644, Behavior and Mechanics of Multifunctional Materials and Composites, 76441A.
|
|
[37]
|
Hossieny N (2010) Morphology and properties of polymer/carbon nanotube nanocomposite foams prepared by super critical carbon dioxide [Thesis]. The Florida State University.
|
|
[38]
|
Nawaby AV, Zhang ZY (2004) Solubility and Diffusivity, In: Gendron R, Thermoplastic Foam Processing: Principles and Development. Boca Raton, FL: CRC Press, 1–42.
|
|
[39]
|
Kumar V, Suh NP (1990) A Process for Making Microcellular Thermoplastic Parts. Polym Eng Sci 30: 1323–1329. doi: 10.1002/pen.760302010

|
|
[40]
|
Kumar V, Weller JE, Montecillo R (1992) Microcellular PVC. J Vinyl Technol 14: 191–197. doi: 10.1002/vnl.730140406

|
|
[41]
|
Schirmer HG, Kumar V (2003) Novel reduced-density materials by solid-state extrusion: Proof-of-concept experiments. Cell Polym 23: 369–385.
|
|
[42]
|
Park CB, Cheung LK (1997) A study of cell nucleation in the extrusion of polypropylene foams. Polym Eng Sci 37: 1–10. doi: 10.1002/pen.11639

|
|
[43]
|
Park CB, Suh NP (1996) Filamentary extrusion of microcellular polymers using a rapid decompressive element. Polym Eng Sci 36: 34–48.
|
|
[44]
|
Chen L, Rende D, Schadler LS, et al. (2013) Polymer nanocomposite foams. J Mater Chem A 1: 3837–3850. doi: 10.1039/c2ta00086e

|
|
[45]
|
Colton JS, Suh NP (1986) The nucleation of microcellular thermoplastic foam: process model and experimental results. Adv Manuf Process 1: 341–364. doi: 10.1080/10426918608953169

|
|
[46]
|
Colton JS, Suh NP (1987) The nucleation of microcellular thermoplastic foam with additives: Part I: Theoretical considerations. Polym Eng Sci 27: 485–492. doi: 10.1002/pen.760270702

|
|
[47]
|
Colton JS, Suh NP (1987) The nucleation of microcellular thermoplastic foam with additives: Part II: Experimental results and discussions. Polym Eng Sci 27: 493–499. doi: 10.1002/pen.760270703

|
|
[48]
|
Bae SS (2005) Preparation of polypropylene foams with micro/nanocellular morphology using a Sorbitol-based nucleating agent [Thesis]. University of Toronto.
|
|
[49]
|
Liu F (1998) Processing of polyethylene and polypropylene foams in rotational molding [Thesis]. University of Toronto.
|
|
[50]
|
Shi J (2017) Ferro-electrets material in human body energy harvesting [Thesis]. University of Southampton.
|
|
[51]
|
Gerhard-Multhaupt R (2002) Less can be more. Holes in polymers lead to a new paradigm of piezoelectric materials for electret transducers. IEEE T Dielect El In 9: 850–859.
|
|
[52]
|
Bauer S, Gerhard-Multhaupt R, Sessler GM (2004) Ferroelectrets: Soft electroactive foams for transducers. Phys Today 57: 37–43.
|
|
[53]
|
Ramadan KS, Sameoto D, Evoy S (2014) A review of piezoelectric polymers as functional materials for electromechanical transducers. Smart Mater Struct 23: 1–26.
|
|
[54]
|
Qiu X, Gerhard R, Mellinger A (2011) Turning polymer foams or polymer-film systems into ferroelectrets: dielectric barrier discharges in voids. IEEE T Dielect El In 18: 34–42. doi: 10.1109/TDEI.2011.5704490

|
|
[55]
|
Qiu X, Mellinger A, Wegener M, et al. (2007) Barrier discharges in cellular polypropylene ferroelectrets: How do they influence the electromechanical properties. J Appl Phys 101: 104112. doi: 10.1063/1.2735410

|
|
[56]
|
Qiu X, Mellinger A, Gerhard R (2008) Influence of gas pressure in the voids during charging on the piezoelectricity of ferroelectrets. Appl Phys Lett 92: 052901. doi: 10.1063/1.2841037

|
|
[57]
|
Montanari GC, Mazzanti G, Ciani F, et al. (2004) Effect of gas expansion on charging behavior of quasi-piezoelectric cellular PP. The 17th Annual Meeting of the IEEE Lasers and Electro-Optics Society, 153–157.
|
|
[58]
|
Zhang P, Xia Z, Qiu X, et al. (2005) Influence of charging parameters on piezoelectricity for cellular polypropylene film electrets. 12th International Symposium on Electrets, 39–42.
|
|
[59]
|
Koliatene F (2009) Contribution à l'étude de l'existence des décharges dans les systèmes de l'avionique 'Contribution to the study of the existence of discharges in avionics systems' [Thesis]. Toulouse University.
|
|
[60]
|
Wegener M, Tuncer E, Gerhard-Multhaupt R, et al. (2006) Elastic properties and electromechanical coupling factor of inflated polypropylene ferroelectrets. 2006 IEEE Conference on Electrical Insulation and Dielectric Phenomena, 752–755.
|
|
[61]
|
Tuncer E, Wegener M (2006) Soft polymeric composites for electro-mechanical applications: predicting and designing their properties by numerical simulations, In: Dillon KI, Soft Condensed Matter: New Research, Nova Science publishers, 217–275.
|
|
[62]
|
Gibson LJ, Ashby M (1997) Cellular Solids: structure and properties, In: Solid state science, Cambridge University Press.
|
|
[63]
|
Lindner M, Hoislbauer H, Schwodiaue R, et al. (2004) Charged cellular polymers with ferroelectretic behavior. IEEE T Dielect El In 11: 255–263. doi: 10.1109/TDEI.2004.1285895

|
|
[64]
|
Xu BX, von Seggern H, Zhukov S, et al. (2013) Continuum modeling of charging process and piezoelectricity of ferroelectrets. J Appl Phys 114: 094103. doi: 10.1063/1.4819441

|
|
[65]
|
Torquato S (2001) Random Heterogeneous Materials: Microstructure and macroscopic properties, New York: Springer Science & Business Media.
|
|
[66]
|
Tuncer E (2005) Numerical calculations of effective elastic properties of two cellular structures. J Phys D Appl Phys 38: 497–503. doi: 10.1088/0022-3727/38/3/023

|
|
[67]
|
Qui X (2016) Polymer Electrets and Ferroelectrets as EAPs: Materials, In: Carpi F, Electromechanically Active Polymers. Polymers and Polymeric Composites: A Reference Series, Springer, Cham.
|
|
[68]
|
Thyssen A, Almdal K, Thomsen EV (2015) Electret Stability Related to the Crystallinity in Polypropylene. 2015 IEEE Sensors, 1–4.
|
|
[69]
|
Fang P (2010) Preparation and Investigation of Polymer-Foam Films and Polymer-Layer Systems for Ferroelectrets [Thesis]. University of Potsdam.
|
|
[70]
|
Mellinger A, Wegener W, Wirges W, et al. (2006) Thermal and Temporal Stability of Ferroelectret Films Made from Cellular Polypropylene/Air Composites. Ferroelectrics 331: 189–199. doi: 10.1080/00150190600737933

|
|
[71]
|
Nakayama M, Uenaka Y, Kataoka S, et al. (2009) Piezoelectricity of ferroelectret porous polyethylene thin film. Jpn J Appl Phys 48: 09KE05.
|
|
[72]
|
Tajitsu Y (2011) Piezoelectric properties of ferroelectret. Ferroelectrics 415: 57–66. doi: 10.1080/00150193.2011.577372

|
|
[73]
|
Brañaa GO, Segoviab PL, Magranera F, et al. (2011) Influence of corona charging in cellular polyethylene film. J Phys Conf Ser 301: 012054. doi: 10.1088/1742-6596/301/1/012054

|
|
[74]
|
Mellinger A, Wegener M, Wirges W, et al. (2011) Thermally stable dynamic piezoelectricity in sandwich films of porous and nonporous amorphous fluoropolymer. Appl Phys Lett 79: 1851–1854.
|
|
[75]
|
Altafim RAP, Qiu X, Wirges W, et al. (2009) Template-based fluoroethylenepropylene piezoelectrets with tubular channels for transducer applications. J Appl Phys 106: 014106.
|
|
[76]
|
Wirges W, Wegener M, Voronina O, et al. (2007) Optimized preparation of elastically soft, highly piezoelectric cellular ferroelectrets from nonvoided poly(ethylene terephthalate) films. Adv Funct Mater 17: 324–329. doi: 10.1002/adfm.200600162

|
|
[77]
|
Wegener M, Wirges W, Dietrich JP, et al. (2005) Polyethylene terephthalate (PETP) foams as ferroelectrets. 12th International Symposium on Electrets, 28–30.
|
|
[78]
|
Fang P, Wegener M, Wirges W, et al. (2007) Cellular polyethylene-naphthalate ferroelectrets: foaming in supercritical carbon dioxide, structural and electrical preparation, and resulting piezoelectricity. Appl Phys Lett 90: 192908. doi: 10.1063/1.2738365

|
|
[79]
|
Fang P, Wirges W, Wegener M, et al. (2008) Cellular polyethylene-naphthalate films for ferroelectret applications: foaming, inflation and stretching, assessment of electromechanically relevant structural features. E-Polymers 8: 487–495.
|
|
[80]
|
Fang P, Qiu X, Wirges W, et al. (2010) Polyethylene-naphthalate (PEN) ferroelectrets: cellular structure, piezoelectricity and thermal stability. IEEE T Dielect El In 17: 1079–1087. doi: 10.1109/TDEI.2010.5539678

|
|
[81]
|
Li Y, Zeng C (2013) Low-temperature CO2-assisted assembly of cyclic olefin copolymer ferroelectrets of high piezoelectricity and thermal stability. Macromol Chem Phys 214: 2733–2738. doi: 10.1002/macp.201300440

|
|
[82]
|
Information of the company Xonano smart foam (USA). Available from: http://www.xonano.com/.
|
|
[83]
|
Dobkin BH, Dorsch A (2011) The promise of mHealth: Daily activity monitoring and outcome assessments by wearable sensors. Neurorehab Neural Re 25: 788–798. doi: 10.1177/1545968311425908

|
|
[84]
|
Patel S, Park H, Bonato P, et al. (2012) A review of wearable sensors and systems with application in rehabilitation. J Neuroeng Rehabil 9: 1–17. doi: 10.1186/1743-0003-9-1

|
|
[85]
|
Li X, Fisher M, Rymer WZ, et al. (2015) Application of the F-response for estimating motor unit number and amplitude distribution in hand muscles of stroke survivors. IEEE T Neur Sys Reh 24: 674–681.
|
|
[86]
|
Jarrasse N, Nicol C, Touillet A, et al. (2017) Classification of phantom finger, hand, wrist, and elbow voluntary gestures in transhumeral amputees with sEMG. IEEE T Neur Sys Reh 25: 71–80. doi: 10.1109/TNSRE.2016.2563222

|
|
[87]
|
Fang P, Ma X, Li X, et al. (2018) Fabrication, structure characterization, and performance testing of piezoelectret-film sensors for recording body motion. IEEE Sens J 18: 401–412. doi: 10.1109/JSEN.2017.2766663

|
|
[88]
|
Information of the company Emfit (Finland). Available from: https://www.emfit.com/.
|
|
[89]
|
Wegener M, Wirges W (2004) Optimized electromechanical properties and applications of cellular polypropylene-a new voided space-charge electret material, In: Fecht HJ, Werner M, The nano-micro interface: Bridging the micro and nano worlds, Wiley-VCH Verlag GmbH & Co. KGaA, 303–317.
|
|
[90]
|
Kim JY (2013) Parylene C as a new piezoelectric material [Thesis]. California Institute of Technology.
|
|
[91]
|
Saarimaki E, Paajanen M, Savijarvi A, et al. (2006) Novel heat durable electromechanical film: processing for electromechanical and electret applications. IEEE T Dielect El In 13: 963–972. doi: 10.1109/TDEI.2006.247820

|
|
[92]
|
Doring J, Bovtun V, Bartusch J, et al. (2010) Nonlinear electromechanical response of the ferroelectret ultrasonic transducers. Appl Phys A-Mater 100: 479–485. doi: 10.1007/s00339-010-5752-7

|
|
[93]
|
Lei W (2017) Ferroelectret nanogenerator (FENG) for mechanical energy harvesting and self-powered flexible electronics [Thesis]. Michigan State University.
|
|
[94]
|
Information of the company B-Band (Finland). Available from: http://www.b-band.com/.
|
|
[95]
|
Kogler A, Buchberger G, Schwodiauer R, et al. (2011) Ferroelectret based Flexible Keyboards and Tactile Sensors. 14th International Symposium on Electrets, 201–202.
|
|
[96]
|
Hillenbrand J, Kodejska M, Garcin Y, et al. (2010) High sensitivity piezoelectret film accelerometers. IEEE T Dielect El In 17: 1021–1027. doi: 10.1109/TDEI.2010.5539670

|
|
[97]
|
Hillenbrand J, Haberzettl S, Motz T, et al. (2011) Electret accelerometers: physics and dynamic characterization. J Acoust Soc Am 129: 3682–3687. doi: 10.1121/1.3585833

|
|
[98]
|
Information of 2020 armor products (USA). Available from: http://www.2020armor.com/.
|
|
[99]
|
Zhuo Q, Tian L, Fang P, et al. (2015) A piezoelectric-based approach for touching and slipping detection in robotic hands. 2015 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), 918–921.
|
|
[100]
|
Ning C, Zhou Z, Tan G, et al. (2018) Electroactive polymers for tissue regeneration: Developments and perspectives. Prog Polym Sci 81: 144–162. doi: 10.1016/j.progpolymsci.2018.01.001

|
|
[101]
|
Wan YP, Zhong Z (2012) Effective electromechanical properties of cellular piezoelectret: A review. Acta Mech Sinica 28: 951–959. doi: 10.1007/s10409-012-0125-4

|









 DownLoad:
DownLoad: