A Global Integration Platform for Optimizing Cooperative Modeling and Simultaneous Joint Inversion of Multi-domain Geophysical Data

1.   Introduction

Rectifying curves have been studied a lot in three-dimensional Euclidean space. Rectifying curve whose definition and equivalent definitions are provided in ^[1]. Chen and Dillen revealed the relationship between the center point of the spatial curve and the rectifying curve in ^[2]. Rectifying curves have many properties in Euclidean space ^[3]. In four-dimensional Euclidean space, İşbilir and Tosun ^[4] studied rectifying curves. Many scholars studied the properties of multiple curves in three-dimensional Minkowski space ^[5,6]. There have also been studies about rectifying curves, such as three-dimensional Minkowski space ^[7,8], three-dimensional hyperbolic space ^[9], and three-dimensional spheres ^[10]. There is a new article about rectifying curves ^[11]. These are all valuable geometric information obtained by analyzing the curvature and the torsion of the regular rectifying curve and the Frenet-Serret formula. If the curve has singularities, then other methods need to be used for research. The definition of framed curves has been given in ^[12]. Framed curves are spatial curves that have moving frames. The framed base curve may have singularities. Next, the rectifying curve was studied by the adapted frame in ^[13].

Inspired by the above work, we study non-lightlike framed rectifying curves. We define the non-lightlike framed rectifying curves, study the construction of the non-lightlike framed rectifying curves, and obtain valuable geometric information.

In Section 2, we review the basic knowledge of non-lightlike framed curves. In Section 3, the non-lightlike framed rectifying curves are defined and their equivalent definitions are given. In Section 4, a method for constructing non-lightlike framed rectifying curves is provided, and examples of regular curves and singular curves are also provided. In Section 5, we define non-lightlike framed helices to obtain the relationship between them and non-lightlike framed rectifying curves. The centrodes of non-lightlike framed rectifying curves are also studied.

All maps and manifolds considered here are differentiable of class $ C^\infty $.

2.   Preliminary

Let $ \mathbb{R}_1^3 $ be Minkowski 3-space with the pseudo scalar product $ \langle, \rangle, $ the pseudo vector product $ \wedge $, and the norm $ ||\quad || $. The pseudo scalar product is equipped with the signature $ (-, +, +) $.

For any nonzero vector $ \mathit{\boldsymbol{a}}\in\mathbb{R}_1^3 $, it is called spacelike, timelike, or lightlike if $ \langle\mathit{\boldsymbol{a}}, \mathit{\boldsymbol{a}}\rangle $ is positive, negative, or zero, respectively. We say the regular curve $ \gamma:I \rightarrow \mathbb{R}_1^3 $ is spacelike, timelike, or lightlike if the vector $ \gamma^{'}(t) $ is spacelike, timelike or lightlike for all $ t\in I $, respectively. For $ {\mathit{\boldsymbol{n}}} \in \mathbb{R}_1^3\backslash\{\mathit{\boldsymbol{0}}\} $, define a set $ P = \{\mathit{\boldsymbol{a}}\in\mathbb{R}_1^3|\langle\mathit{\boldsymbol{a}}, \mathit{\boldsymbol{n}}\rangle = 0\} $. It is obvious that $ P $ is a plane in $ \mathbb{R}_1^3 $. The vector $ \mathit{\boldsymbol{n}} $ is called the pseudo normal vector of the plane $ P $. The plane $ P $ is called spacelike, timelike, or lightlike if the vector $ \mathit{\boldsymbol{n}} $ is timelike, spacelike, or lightlike, respectively.

There are three pseudo spheres in $ \mathbb{R}_1^3 $:

and

We call them de Sitter 2-space, (open) lightcone, and hyperbolic 2-space, respectively. Let $ \Delta = \{(\boldsymbol{\beta}_1, \boldsymbol{\beta}_2)\in\mathbb{R}_1^3\times\mathbb{R}_1^3|\langle\boldsymbol{\beta}_1, \boldsymbol{\beta}_2\rangle = 0, ||\boldsymbol{\beta}_1|| = 1, ||\boldsymbol{\beta}_2|| = 1\} $ and $ \gamma:I \rightarrow \mathbb{R}_1^3 $ be a non-lightlike curve.

Definition 2.1. We call $ (\gamma, \mathit{\boldsymbol{\beta}}_1, \mathit{\boldsymbol{\beta}}_2):I \rightarrow \mathbb{R}_1^3\times\Delta $ a non-lightlike framed curve if $ \langle\gamma^{'}(t), \mathit{\boldsymbol{\beta}}_1(t)\rangle = 0 $, $ \langle\gamma^{'}(t), \mathit{\boldsymbol{\beta}}_2(t)\rangle = 0 $ for any $ t\in I $. We call $ \gamma:I \rightarrow \mathbb{R}_1^3 $ a non-lightlike framed base curve if there exists $ (\mathit{\boldsymbol{\beta}}_1, \mathit{\boldsymbol{\beta}}_2):I \rightarrow \Delta $ such that $ (\gamma, \mathit{\boldsymbol{\beta}}_1, \mathit{\boldsymbol{\beta}}_2) $ is a non-lightlike framed curve.

Define $ \boldsymbol{\mu}(t) = \mathit{\boldsymbol{\beta}}_1(t)\wedge\mathit{\boldsymbol{\beta}}_2(t) $. There exists a function $ \alpha : I \rightarrow \mathbb{R} $ satisfying $ \gamma^{'}(t) = \alpha(t)\boldsymbol{\mu}(t) $. $ \{\mathit{\boldsymbol{\beta}}_1(t), \mathit{\boldsymbol{\beta}}_2(t), \boldsymbol{\mu}(t)\} $ is a moving frame along $ \gamma. $ Frenet-type formulas are

where

$ (l_1, l_2, l_3, \alpha): I \rightarrow \mathbb{R}^4 $ is called the curvature of $ (\gamma, \mathit{\boldsymbol{\beta}}_1, \mathit{\boldsymbol{\beta}}_2) $. If $ \boldsymbol{\mu}(t) $ is spacelike (timelike), we call $ \gamma $ a spacelike (timelike) framed base curve.

We know $ t_0 $ is a singular point of $ \gamma $ if and only if $ \alpha(t_0) = 0 $.

Proposition 2.2. $ \gamma:I \rightarrow \mathbb{R}_1^3 $ is a non-lightlike regular curve, and $ (\gamma, \mathit{\boldsymbol{\beta}}_1, \mathit{\boldsymbol{\beta}}_2):I \rightarrow \mathbb{R}_1^3\times\Delta $ is a non-lightlike framed curve. The relations between the curvature $ (l_1, l_2, l_3, \alpha) $ of $ (\gamma, \mathit{\boldsymbol{\beta}}_1, \mathit{\boldsymbol{\beta}}_2) $ and the curvature $ \kappa $ and the torsion $ \tau $ of $ \gamma $ are

We assume $ l_2^2(t)\neq\sigma l_3^2(t) $ and denote $ \varepsilon = {\rm sgn}(l_2^2-\sigma l_3^2)(t) $.

Definition 2.3. $ (\gamma, \mathit{\boldsymbol{\beta}}_1, \mathit{\boldsymbol{\beta}}_2):I \rightarrow \mathbb{R}_1^3\times\Delta $ is a non-lightlike framed curve, and its curvature is $ (l_1, l_2, l_3, \alpha) $. Let

We call $ \overline{\mathit{\boldsymbol{\beta}}}_1 $ direction the principal normal direction of $ (\gamma, \mathit{\boldsymbol{\beta}}_1, \mathit{\boldsymbol{\beta}}_2) $ and $ \overline{\mathit{\boldsymbol{\beta}}}_2 $ direction the binormal direction of $ (\gamma, \mathit{\boldsymbol{\beta}}_1, \mathit{\boldsymbol{\beta}}_2) $.

We have $ \boldsymbol{\mu}(t) = \overline{\mathit{\boldsymbol{\beta}}}_1(t) \wedge \overline{\mathit{\boldsymbol{\beta}}}_2(t) $. $ \{\overline{\mathit{\boldsymbol{\beta}}}_1(t), \overline{\mathit{\boldsymbol{\beta}}}_2(t), \boldsymbol{\mu}(t)\} $ is called the Frenet-type frame along $ \gamma $. Frenet-type formulas are

where

Then $ (L_1, L_2, 0, \alpha) $ is the curvature of $ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2) $.

Remark 2.4. $ (\gamma, \mathit{\boldsymbol{\beta}}_1, \mathit{\boldsymbol{\beta}}_2):I \rightarrow \mathbb{R}_1^3\times\Delta $ is a non-lightlike framed curve, and its curvature is $ (l_1, l_2, 0, \alpha) $. If $ l_2(t) > 0 $, then $ \overline{\mathit{\boldsymbol{\beta}}}_1(t) = \mathit{\boldsymbol{\beta}}_1(t) $ and $ \overline{\mathit{\boldsymbol{\beta}}}_2(t) = \mathit{\boldsymbol{\beta}}_2(t) $. If $ l_2(t) < 0 $, then $ \overline{\mathit{\boldsymbol{\beta}}}_1(t) = -\mathit{\boldsymbol{\beta}}_1(t) $ and $ \overline{\mathit{\boldsymbol{\beta}}}_2(t) = -\mathit{\boldsymbol{\beta}}_2(t). $

In this article, we only study the non-lightlike framed curve $ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2) $ and its frame is the Frenet-type frame $ \{\overline{\mathit{\boldsymbol{\beta}}}_1(t), \overline{\mathit{\boldsymbol{\beta}}}_2(t), \mathit{\boldsymbol{\mu}}(t)\} $.

Remark 2.5. $ \gamma:I \rightarrow \mathbb{R}_1^3 $ is a non-lightlike regular curve and $ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2):I \rightarrow \mathbb{R}_1^3\times\Delta $ is a non-lightlike framed curve. Let $ l_3 = 0 $ be in Proposition 2.2. We have the relations among the curvature $ \kappa $, the torsion $ \tau $ of $ \gamma $ and the curvature $ (L_1, L_2, 0, \alpha) $ of $ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2) $ are

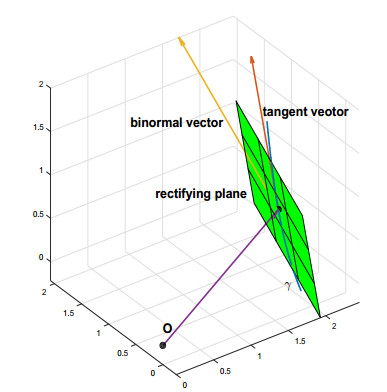
For a non-lightlike framed curve $ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2):I \rightarrow \mathbb{R}_1^3\times\Delta $, the rectifying plane of $ \gamma $ at $ t_0 $ is the plane through $ \gamma(t_0) $ and spanned by $ \overline{\mathit{\boldsymbol{\beta}}}_2(t_0) $ and $ \mathit{\boldsymbol{\mu}}(t_0) $.

3.   Non-lightlike framed rectifying curves

Definition 3.1. $ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2):I \rightarrow \mathbb{R}_1^3\times\Delta $ is a non-lightlike framed curve. We call $ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2) $ a non-lightlike framed rectifying curve if $ \gamma $ satisfies

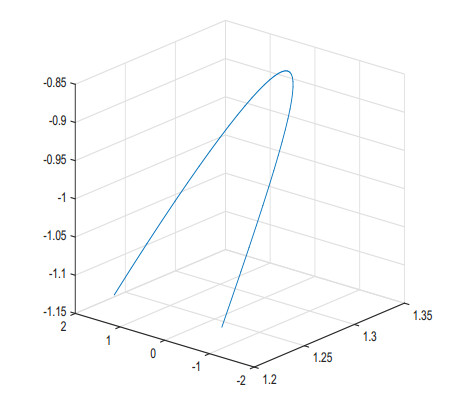
for two functions $ \psi(t), \phi(t): I \rightarrow \mathbb{R} $. $ \gamma $ is called a base curve of a non-lightlike framed rectifying curve (Figure 1).

We call $ f(t) = \langle\gamma(t), \gamma(t)\rangle $ the distance squared function of a non-lightlike framed curve $ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2) $.

Theorem 3.2. $ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2):I \rightarrow \mathbb{R}_1^3\times\Delta $ is a non-lightlike framed curve. The following statements are equivalent.

(1) $ \langle\gamma(t), \boldsymbol{\mu}(t)\rangle^{'} = \sigma\alpha(t). $

(2) The distance squared function satisfies

(3) $ \langle\gamma(t), \overline{\mathit{\boldsymbol{\beta}}}_2(t)\rangle = \phi\varepsilon\delta, \; \phi \in \mathbb{R}\backslash\{0\}. $

(4) $ \gamma(t) $ is a base curve of a non-lightlike framed rectifying curve.

Proof. Let $ \gamma(t) $ be a base curve of a non-lightlike framed rectifying curve. We know there exist two functions $ \psi(t) $ and $ \phi(t) $ such that

According to the Frenet-type formulas and deriving (3.1), we have

Then

From the first equation of (3.2), we obtain $ \langle\gamma, \mathit{\boldsymbol{\mu}}\rangle^{'}(t) = \sigma\psi^{'}(t) = \sigma\alpha(t) $. This proves the statement (1).

By (3.1) and (3.2), we can obtain that

If $ \phi = 0 $, then $ \psi(t) = 0 $ and $ \gamma(t) $ is a point. So $ \phi\neq0 $. This proves statements (2) and (3).

Conversely, we assume the statement (1) holds, then

By assumption, we obtain $ \langle\gamma(t), \overline{\mathit{\boldsymbol{\beta}}}_1(t)\rangle = 0 $. So $ \gamma(t) $ is a base curve of a non-lightlike framed rectifying curve.

If the statement (2) holds, then

Then,

So we get $ \langle\gamma(t), \overline{\mathit{\boldsymbol{\beta}}}_1(t)\rangle = 0. \; \gamma(t) $ is a base curve of a non-lightlike framed rectifying curve.

If the statement (3) holds, $ \langle\gamma(t), \overline{\mathit{\boldsymbol{\beta}}}_2(t)\rangle = \phi\sigma\varepsilon\delta. $ By taking the derivative, we have

So $ \langle\gamma(t), \overline{\mathit{\boldsymbol{\beta}}}_1(t)\rangle = 0. \; \gamma(t) $ is a base curve of a non-lightlike framed rectifying curve. □

Remark 3.3. $ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2) $ is a non-lightlike framed rectifying curve. If the base curve of a non-lightlike framed rectifying curve $ \gamma $ is singular at $ t_0 $, then from Eq (3.2) and the statement (2) in Theorem 3.2, we have

So $ \left(\dfrac{L_1(t_0)}{L_2(t_0)}\right)^{'} = 0 $. Moreover, we know

So $ f^{'}(t_0) = 0 $.

4.   The construction of non-lightlike framed rectifying curves

Theorem 4.1. $ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2):I \rightarrow \mathbb{R}_1^3\times\Delta $ is a non-lightlike framed rectifying curve. $ \gamma(t) $ is a base curve of a non-lightlike framed rectifying curve if and only if $ \gamma(t) $ can be expressed as one of the following two equations

where $ M $ is a constant, $ \rho \in \mathbb{R}\backslash\{0\} $ and $ \mathit{\boldsymbol{y}}(t) $ is a spacelike framed base curve on $ S_1^2 $. Or

where $ M $ is a constant, $ \phi \in \mathbb{R}\backslash\{0\} $ and $ \mathit{\boldsymbol{y}}(t) $ is a spacelike (timelike) framed base curve on $ H_0^2 $ ($ S_1^2 $).

Proof. First, we prove the first equation. Let $ \gamma(t) $ be a base curve of a spacelike framed rectifying curve, which has a spacelike rectifying plane. So $ \langle\gamma, \gamma\rangle(t) = (\psi^2(t)+\rho^2)(t) $, where $ \rho \in \mathbb{R}\backslash\{{0}\} $. Let $ \mathit{\boldsymbol{y}}(t) = \left(\dfrac{1}{({\psi}^2+\rho^2)^{\tfrac{1}{2}}}\gamma\right)(t) $ be a spacelike framed base curve on $ S_1^2 $. We have

Since $ \gamma^{'}(t) = \alpha(t)\boldsymbol{\mu}(t) $ and $ \mathit{\boldsymbol{y}}^{'}(t) $ is orthogonal to $ \mathit{\boldsymbol{y}}(t) $, we can obtain

So

We only consider $ \rho\alpha(t)\geq0 $, and it is similar for $ \rho\alpha(t)\leq0 $. Then

That is

So

Conversely, let $ ({\mathit{\boldsymbol{y}}}, \boldsymbol{\beta}_{y_1}, \boldsymbol{\beta}_{y_2}) $ be a spacelike framed curve and $ \gamma(t) $ be defined by

Let $ \overline{\psi}(t) = \rho(\tan^2(\int||\mathit{\boldsymbol{y}}^{'}(t)||{\rm d}t+M)) $ and $ \overline{\alpha}(t) = \overline{\psi}^{'}(t) $. Then

Since $ \mathit{\boldsymbol{y}}(t) $ is also a spacelike framed curve, we define that $ \mathit{\boldsymbol{y}}^{'}(t) = \psi(t)\boldsymbol{\mu}_{y}(t) $, where $ \boldsymbol{\mu}_{y}(t) = \mathit{\boldsymbol{\beta}}_{y_1}(t) \wedge\mathit{\boldsymbol{\beta}}_{y_2}(t) $. We can obtain

and

Therefore, we denote that $ \mathit{\boldsymbol{y}}^{'}(t) = \left(\dfrac{\rho\overline{\alpha}}{\overline{\psi}^2+\rho^2}\boldsymbol{\mu}_{y}\right)(t) $. That is $ y(t) = \left(\dfrac{\rho\overline{\alpha}}{\overline{\psi}^2(t)+\rho^2}\right)(t) $. Then we have

Hence, we can calculate that $ \langle\gamma, \mathit{\boldsymbol{\mu}}\rangle^2(t) = \overline{\psi}(t) $. Since $ \langle\gamma, \gamma\rangle(t) = (\overline{\psi}^2+\rho^2)(t) $, we have

It indicates that the function satisfies the statement (2) in Theorem 3.2. So $ \gamma(t) $ is a base curve of a spacelike framed rectifying curve.

Next we prove the second equation. Let $ \gamma(t) $ be the base curve of a spacelike framed rectifying curve, which has a timelike rectifying plane and a spacelike position vector. (We only prove this case, and the proof for other cases is similar to it.) So $ \langle\gamma, \gamma\rangle(t) = (\psi^2-\phi^2)(t) $, where $ \phi \in \mathbb{R}\backslash\{{0}\} $. Let $ \mathit{\boldsymbol{y}}(t) = \left(\dfrac{1}{({\psi}^2-\phi^2)^{\tfrac{1}{2}}}\gamma\right)(t) $ be a spacelike framed base curve on $ S_1^2 $. We have

Since $ \gamma^{'}(t) = (\alpha\boldsymbol{\mu})(t) $ and $ \mathit{\boldsymbol{y}}^{'}(t) $ is orthogonal to $ \mathit{\boldsymbol{y}}(t) $,

So

and

Then,

So

Conversely, we can obtain the proof of this section by referring to the proof of the first equation. □

Remark 4.2. If $ \gamma(t) $ is a base curve of a spacelike framed rectifying curve, which has a timelike rectifying plane and a lightlike position vector, then $ \langle \gamma(t), \gamma(t)\rangle = 0 $. That means $ \psi^2(t) = \phi^2 $, $ \alpha(t) = 0 $, then $ \gamma(t) $ is a point. So $ \gamma(t) $ does not exist.

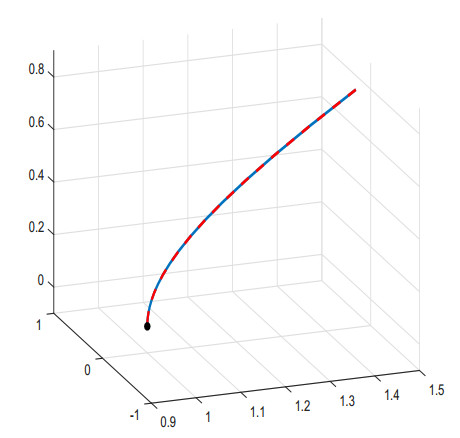
Example 4.3. Let $ {\mathit{\boldsymbol{y}}}_1(t) = \left(-\dfrac{\sqrt{3}}{2}, \dfrac{\sqrt{7}}{2}\cos2t, \dfrac{\sqrt{7}}{2}\sin2t\right), t\in\left(-\dfrac{\pi}{2\sqrt{3}}, \dfrac{\pi}{2\sqrt{3}}\right) $ be a curve on $ S_1^2 $. We have $ ||\mathit{\boldsymbol{y}}_1^{'}(t)|| = \sqrt{7} $. Let $ \rho = 1 $ and $ M = 0 $. We have the curve

is a base curve of a non-lightlike framed rectifying curve in $ \mathbb{R}_1^3 $ (Figure 2).

Example 4.4. Let $ \mathit{\boldsymbol{y}}_2(t) = (\sinh t^2, \cosh t^2, 0), t\in\left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right) $ be a curve on $ S_1^2 $. We have $ ||\mathit{\boldsymbol{y}}_2^{'}(t)|| = 2|t| $. Let $ \rho = 1 $ and $ M = 0 $. We have the curve

is a base curve of a non-lightlike framed rectifying curve with a singular point $ \mathbb{R}_1^3 $ (Figure 3).

5.   Non-lightlike framed rectifying curves versus non-lightlike framed helices and centrodes

Definition 5.1. $ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2):I \rightarrow \mathbb{R}_1^3\times\Delta $ is a non-lightlike framed curve. $ \gamma $ is called a non-lightlike framed helix if there exists a fixed unit vector $ \boldsymbol{\eta} $ satisfying

where $ p \in \mathbb{R}\backslash\{0\} $.

Remark 5.2. For a non-lightlike framed curve $ (\gamma, \mathit{\boldsymbol{\beta}}_1, \mathit{\boldsymbol{\beta}}_2) $, we can also call $ \gamma $ a non-lightlike framed helix if there exists a fixed unit vector $ \boldsymbol{\eta} $ satisfying

where $ p \in \mathbb{R}\backslash\{0\} $.

$ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2):I \rightarrow \mathbb{R}_1^3\times\Delta $ is a non-lightlike framed curve with the curvature $ (L_1, L_2, 0, \alpha) $. $ \gamma $ is a non-lightlike framed helix. We consider the ratio $ \dfrac{L_1(t)}{L_2(t)} $.

Since

Then

$ \mathit{\boldsymbol{\eta}} $ is located in the plane, and the plane has basis vectors $ \boldsymbol{\mu}(t) $ and $ \overline{\mathit{\boldsymbol{\beta}}}_2(t) $. Since $ \langle\boldsymbol{\mu}(t), \mathit{\boldsymbol{\eta}}\rangle = p $, we have $ \langle\overline{\mathit{\boldsymbol{\beta}}}_2(t), \mathit{\boldsymbol{\eta}}\rangle $ is a constant, denoted by $ p_1 $. If $ p_1 = 0 $, then $ \boldsymbol{\mu}(t) = \dfrac{\sigma}{p}\mathit{\boldsymbol{\eta}} $. At this point, $ \gamma $ is a segment of a straight line. So we always assume $ p_1\neq0 $. We take the derivative of (5.1), so

Then

By Theorem 3.2, we can obtain $ \gamma(t) $ is a base curve of the non-lightlike framed rectifying curve if and only if

where $ c_1, c_2 \in \mathbb{R} $, $ c_1\neq0 $.

Proposition 5.3. $ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2):I \rightarrow \mathbb{R}_1^3\times\Delta $ is a non-lightlike framed curve and its curvature is $ (L_1, L_2, 0, \alpha) $. The curvature satisfies $ \left(\dfrac{L_1(t)}{L_2(t)}\right)^{'} = c_1\alpha(t). $

(1) If $ c_1 = 0 $, then $ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2) $ is a non-lightlike framed helix.

(2) If $ c_1\neq0 $, then $ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2) $ is a non-lightlike framed rectifying curve.

Definition 5.4. $ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2):I \rightarrow \mathbb{R}_1^3\times\Delta $ is a non-lightlike framed curve and its curvature is $ (L_1, L_2, 0, \alpha) $. We call $ {\mathit{\boldsymbol{d}}}(t) $ the centrode of $ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2) $ if

Proposition 5.5. $ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2):I \rightarrow \mathbb{R}_1^3\times\Delta $ is a non-lightlike framed curve, and its curvature is $ (L_1, L_2, 0, \alpha) $. Where $ L_1(t) $ is a nonzero constant and $ L_2(t) $ is a nonconstant function.

(1) Let $ {\mathit{\boldsymbol{d}}}(t) = (L_1\boldsymbol{\mu}+L_2\overline{\mathit{\boldsymbol{\beta}}}_2)(t) $ be the centrode of $ (\gamma, \overline{\mathit{\boldsymbol{\beta}}}_1, \overline{\mathit{\boldsymbol{\beta}}}_2) $. Then $ \mathit{\boldsymbol{d}}(t) $ is a base curve of a non-lightlike framed rectifying curve.

(2) The base curve of any non-lightlike framed rectifying curve in $ \mathbb{R}_1^3 $ is the centrode of some non-lightlike framed curve.

6.   Conclusions

Future research could extend the concept of non-lightlike framed rectifying curves to high-dimensional Minkowski space or it could study lightlike framed rectifying curves. This provides assistance in studying the properties and classification of higher-dimensional non-lightlike framed rectifying curves.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant No. 11671070).

Conflict of interest

The authors declare that there is no conflict of interest.