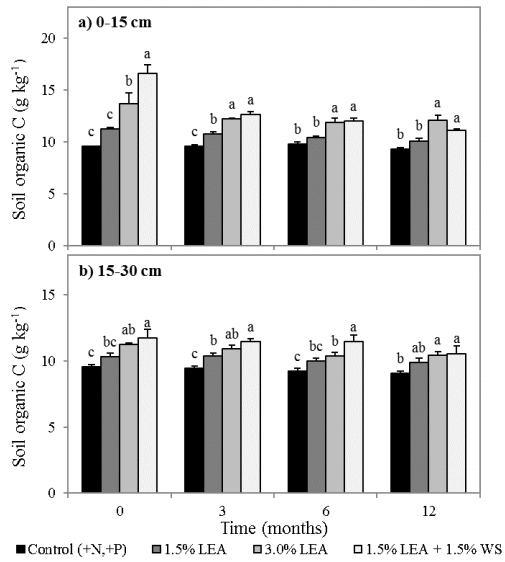
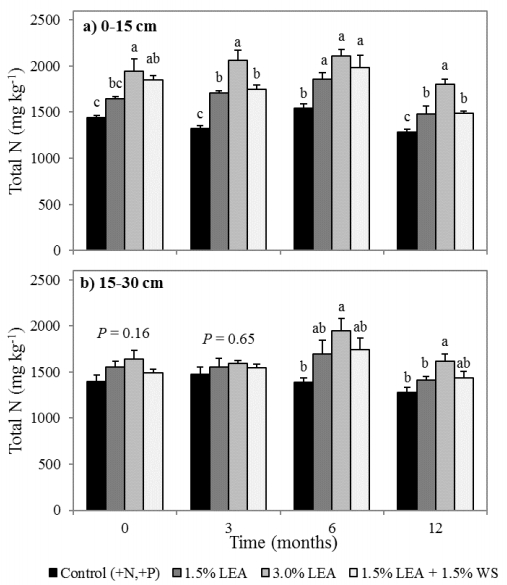
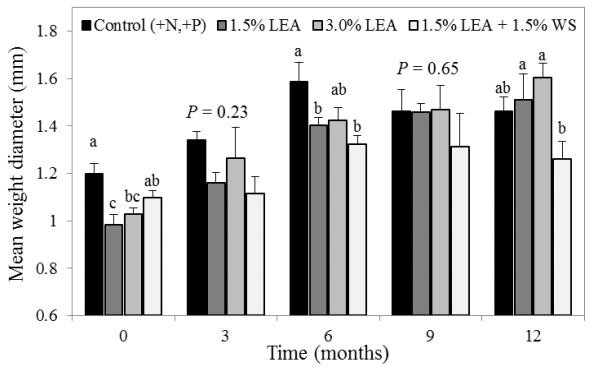
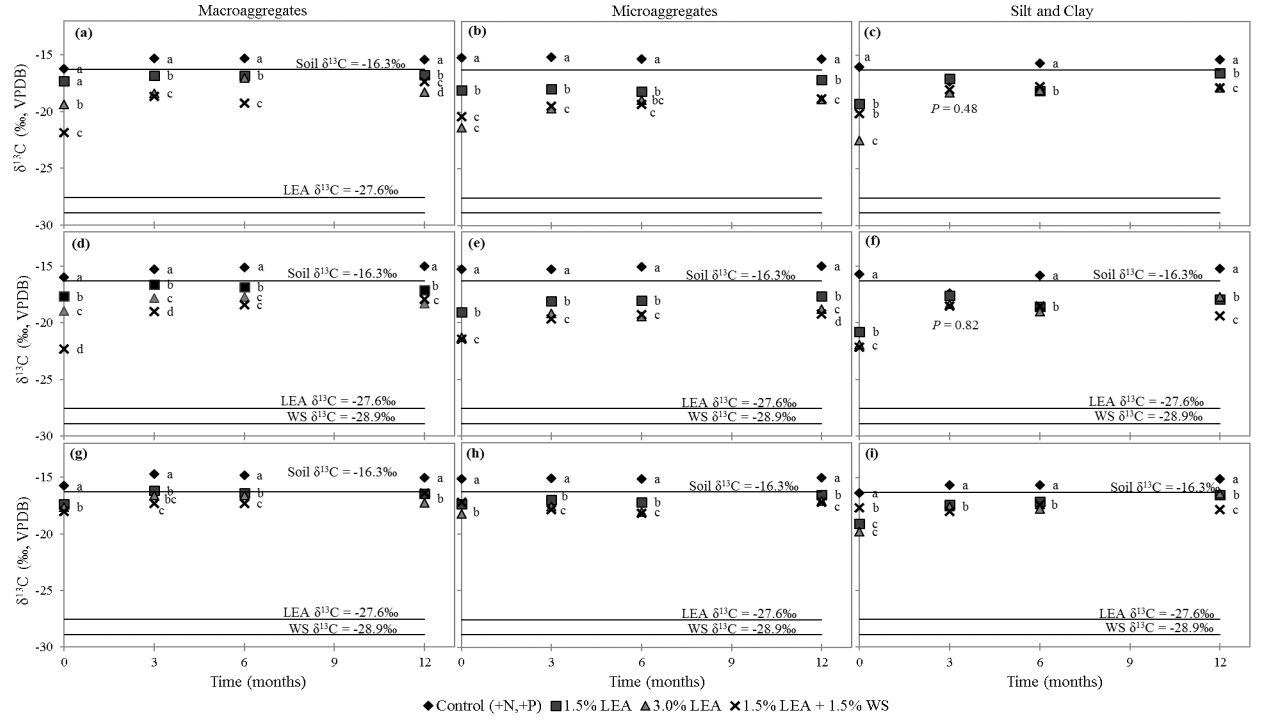
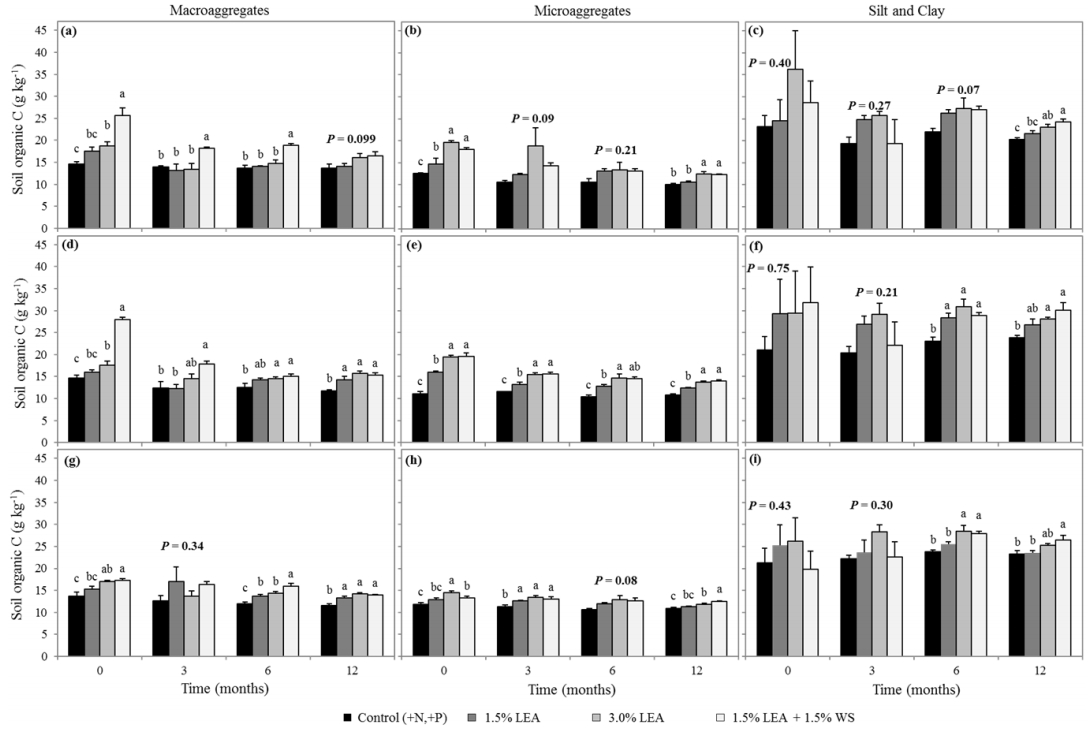
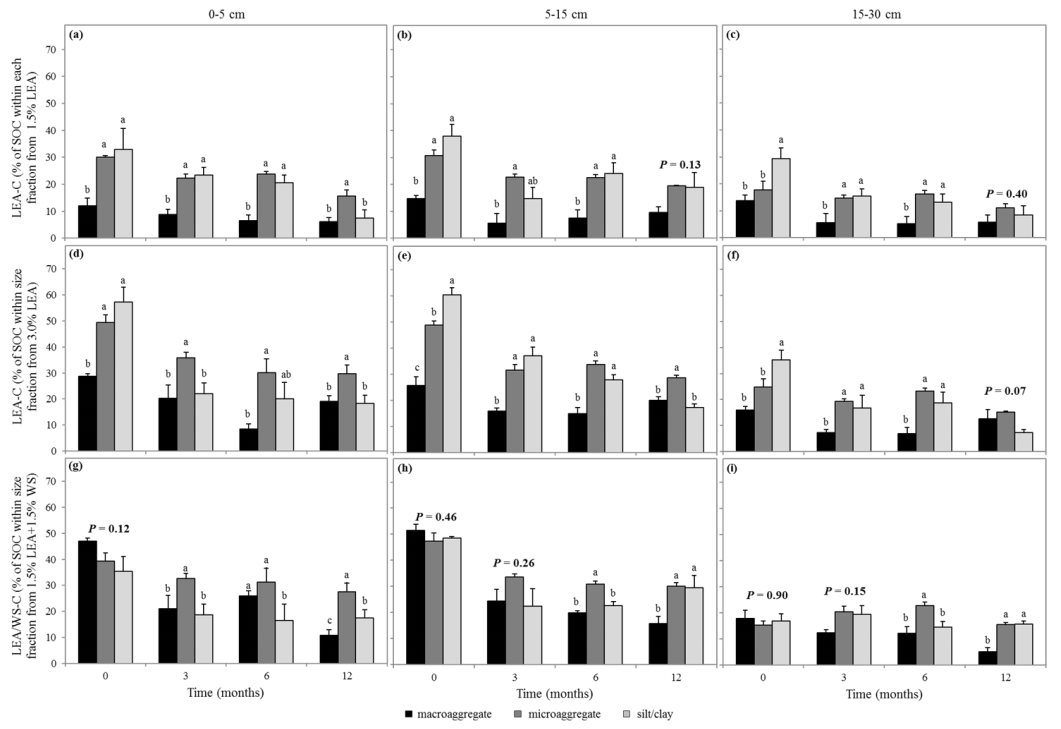
Soil organic C (SOC) storage results when organic matter inputs to soil exceed losses through decomposition, and is strongly influenced by organic matter effects on soil aggregation. We evaluated the initial effects of lipid-extracted algae (LEA), a byproduct of biofuel production, on soil aggregate formation and SOC storage. In situ field incubations were conducted by amending soil with (1) 1.5% LEA, (2) 3.0% LEA, (3) 1.5% LEA + 1.5% wheat straw (WS) and (4) soil plus inorganic N (140 kg ha−1 NH4NO3) and P [112 kg ha−1 Ca(H2PO4)2·H2O] as the control. Soil samples were collected 0, 3, 6, 9, and 12 months after treatment application at 0–5, 5–15, and 15–30 cm. Soil was separated into macroaggregate (>250 µm), microaggregate (250–53 µm), and silt and clay (<53 µm) fractions by dry-sieving, and mean weight diameter was calculated. Soils and soil fractions were analyzed to determine C concentrations and associated δ13C values. Mean weight diameter 12 months after 3.0% LEA application was greater than the 1.5% LEA + 1.5% WS addition at the 5–15 cm depth. Soil amended with 1.5% LEA, 3.0% LEA or 1.5% LEA + 1.5% WS resulted in greater SOC after 12 months for all soil size fractions and depths. δ13C indicated that most LEA-C was initially associated with the silt and clay fraction, but later became more strongly associated with the macro- and microaggregate fractions after 12 months. Soil application of LEA enhanced initial aggregate formation and SOC storage by increasing aggregate MWD and macro- and microaggregate associated SOC over time. As the world population grows and resources become more limited, use of alternative energy sources, soil conservation, and environmental protection must be top research priorities. Our research emphasized all three and demonstrated that LEA can enhance soil structure and C storage.
1.
Introduction
Load frequency control (LFC) is significant for the safe and stable work of the power grids [1,2,3]. With the continuous breakthrough of new energy technology, new energy power generation methods are gradually combined with traditional power generation methods and the penetration rate of modern smart grids continues to increase. Wind power and photovoltaic power are the most widely used forms of new energy generation. However, wind energy and photovoltaic energy are characterized by dispersion, randomness, fluctuation and intermittency [4], which can affect the power grid, especially the frequency.
Usually, when the frequency of the power system fluctuates, the aggregator load changes its working state according to the scheduling instruction to prevent frequency fluctuation [5,6]. Most dynamic demand control models have been with thermostatically controlled devices, with air conditioning loads (ACs) accounting for a huge percentage of them [7,8]. However, most literature focused on how ACs can be controlled based on optimized thought, such as the method based on the load frequency modulation model [9]. Only a few studies have applied ACs to resolve external perturbations [10,11].
With the progress of ultra-high voltage technology and the increasing proportion of new energy in power generation [12,13,14], the communication data between power grid systems has become more complex, which also increases the communication pressure between power grids. In recent years, there has been a growing interest in event-triggered mechanisms (ETM) due to their potential in reducing communication and computation resources while maintaining stability and performance in complex systems [15,16,17,18,19]. ETM is designed to trigger actions and update processes in a system only when certain predefined conditions, or events, are met rather than at fixed time intervals. This smart adaptive strategy is particularly beneficial for systems in which resources are constrained or in dynamic environments where unnecessary updates could be costly. Kazemy et al. [15] have addressed synchronization of master-slave neural networks under deception attacks using event-triggered output feedback control to enhance stability and resilience.
While considering the limited network resources, we should also consider the security problems faced by networked systems [20]. Especially in recent years, industrial open networks have been attacked frequently. At present, network attacks are mainly divided into denial-of-service (DoS) attacks and spoofing attacks. DoS attacks can cause the loss of transmitted data [21], while spoofing attacks are launched by attackers that attempt to disrupt the availability of data [22]. Foroush and Martinez [23] showed that the general security problem of networked is DoS attack, which attempts to transmit a large amount of invalid data and intentionally interfere with network communication resources. Persis and Tesi [24] proved that on the premise of ensuring the asymptotic stability of the system, and the average active time of DoS attacks cannot exceed a certain percentage. In recent years, the research on the security of event-triggered networked systems has made some progress [15].
Inspired by the analysis presented above, this paper explores the application of an observer-based ETM for secure LFC in power systems, with the aim of ensuring the safety and stability of the power system. Considering the inherent instability caused by the increasing penetration of renewable energy in the grid, we treat it as a perturbation. In addition, this study proposes the integration of AC demand response as a control strategy to effectively regulate system frequency fluctuations. Additionally, this paper addresses key challenges related to network bandwidth limitations and potential DoS attacks by incorporating the ETM. A novel aspect of this work is the application of ETM to the observer rather than directly to the system state to mitigate the complexity and impracticalities associated with direct state measurement in real-world applications. The contribution of this paper is as follows:
ⅰ) The volatility associated with renewable energy generation is modeled as a perturbation, accounting for its unpredictable nature in the power system. To enhance the LFC, ACs demand response is incorporated as an effective tool to dynamically adjust the system's frequency in response to fluctuating generation conditions, thereby improving overall system resilience.
ⅱ) In contrast to conventional ETM that rely on direct measurement of system states, this paper introduces an observer-based ETM. By using an observer to estimate system states, this approach avoids the challenges and limitations of directly measuring these values, offering a practical solution for real-time control in large-scale, decentralized power networks.
Notations. U>0 means the matrix U is positive definite. ∗ stands for the corresponding symmetric term in the matrix. diag{⋯} stands for diagonal matrix.
2.
Problem formulation
2.1. Model description
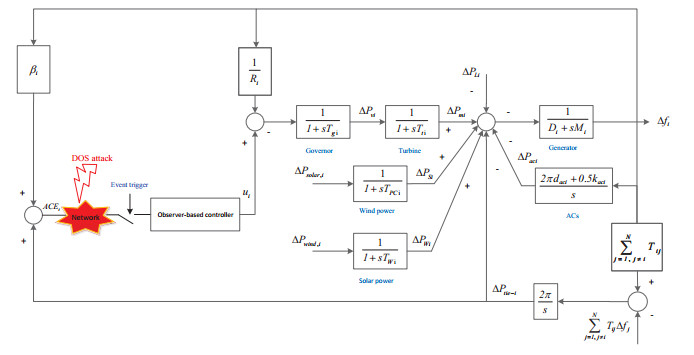
First, considering the random disturbance of wind power and photovoltaic power generation, a multi-area smart grid control model is established with ACs participating in grid frequency regulation, as shown in Figure 1 [25]. System parameters and meanings are shown in Table 1, where kaci=micpikEER.
According to Figure 1, we can obtain
where Daci=2πdaciMi, Tii=∑nj=1,j≠iTij,i,j=1,2,…,n. Define
Then, we can obtain that
where
From (2.2), the state-space form of multi-area ACs LFC model can be described as
with
2.2. Full-order state observer
The full-order state observer is constructed as
where ˆy(t) is the observer output; ˆx(t) is the observer state and L is the observer gain to be solved.
2.3. Observer-based ETM under DoS attacks
In this paper, inspired by [26,27], and periodic event-triggered control schemes [28], we select the ETM activations:
where the difference between the most recent data sample and the current one is referred to as ζ(t), i.e., ζ(t)=ˆx(tk+lh)−ˆx(tk), lh is the intervals between tk and tk+1, l∈N,ikh∈(tk,tk+1], and σ is a threshold parameter.
Remark 1. Unlike traditional ETM that rely on state controllers, this paper introduces a novel approach using observer packets for triggering. This approach leverages the observer pattern, which offers significant advantages in terms of modularity and flexibility. Specifically, the observer pattern enables the seamless addition of new observers to the system without disrupting or modifying other components, ensuring a high degree of decoupling. Similarly, the observed object itself is free to evolve or modify its internal implementation without causing any adverse effects on the observers.
In addition, consider the time-varying delay dk caused by the network between the observer and the event generator [29]. Define d(t) as follows:
where I1=[tk+dk,tk+dk+h), Il2=[tk+dk+lh,tk+dk+lh+h), I2=∪l=m−1l=1Il2, I3=[tk+dk+mh,tk+1+dk+1), [tk+dk,tk+1+dk+1)=I1∪I2∪I3. Moreover, ˆx(tk) and ˆx(tk+ιh) with ι=1,2,…,m satisfy (2.5); dm (dM) denotes the lower (upper) bound on the time delay.
Remark 2. In a multi-area power system, data transmission is routine, but network delays are inevitable. These delays can arise from factors like communication latency or network congestion, and if ignored, they may compromise the accuracy of the measured data. In this study, we define the delay as dk and focus on the case where dk is shorter than the sampling interval. This ensures that the integrity of the data sequence is preserved, with each measurement arriving and being processed within its designated sampling period.
For t∈[tk+dk,tk+1+dk+1), we can define
In what follows, inspired by [30], the observer-based ETM u(t) can be written as
where K is the control gain matrix.
Based on (2.6) and (2.7), the observer-based ETM u(t) can be rewritten as
For a DOS attack in a network, define τ(ikh) as the attack state, τ(ikh)=1 as the attack occurred, and τ(ikh)=0 as the attack did not occur. In a typical power system, most DoS attacks fail to achieve their purpose, and only a fraction of these attacks cause notable disruptions. We divide DoS attacks into the following four types:
In addition, the energy of general DoS attacks is limited. Facing such attacks, we introduce elastic variable ζDoS(t) on the event triggering mechanism to represent the packet loss and delay caused by DoS attacks on the system [31]. We can obtain
where ΔDoS denotes the longest duration of a DoS attack and tDoSk+1 refers to an upcoming sampling moment affected by DoS.
2.4. Modeling augmented systems
Substituting (2.8) into sysetm (2.3) yields
Substituting (2.8) into system (2.4) yields
Define the state error as δ(t)=x(t)−ˆx(t), then
Define the augmented state as ˜xT(t)=[xT(t)δT(t)], the augmented system is
where
Definition 1 [32,33] For an arbitrary initial condition, given γ>0, the augmented system (2.15) is thought to be stable with H∞ performance if the following two conditions are met:
1) for ω(t)=0, the system is asymptotically stable;
2) for ω(t)∈ℓ2[0,∞), the following condition is satisfied:
Lemma 1. [34] For a given time delays constant dm and dM satisfying d(t)∈[dm,dM], for dM>dm>0, there exist matrices R2 and H when
for which the following inequality holds:
3.
Main results
Two theorems are given in this section. Theorem 1 illustrates the stability and H∞ performance of the augmented system, and Theorem 2 gives the design of an observer-based controller.
Theorem 1. For some given positive constants σ, dm and dM, the augmented system (2.15) is asymptotically stable with an H∞ performance index γ, if there exist positive definite matrices P, Q1, Q2, R1, R2, H and V with appropriate dimensions such that
where
Proof. Select Lyapunov function as
From the augmented system (2.15), we have
Using Jessen inequality, Lemma 1 and the Schur complement theorem, at the same time to join the event trigger condition, it can be concluded that
where
Further, we achieve
According to (3.4) and (3.5), the presence of λ>0 ensures that ˙V(t)<0 is satisfied when ω(t)=0, and we can achieve limt→∞V(t)=0.
By Definition 1, the augmented system (2.15) is asymptotically stable.
When ω(t)≠0, both sides of (3.5) integrate from 0 to +∞,
At zero original condition, we obtain
Since Ω<0, there exists a proper positive ε so that
Multiply the upper expression by eεt and integrate the result. Subsequently,
It is evident that
In the presence of an attack, the system's security performance bounds uniformly, with a degradation no greater than Δ. This finishes the proof.
Theorem 2. For some given positive constants σ, dm and dM, the augmented system (2.15) is asymptotical stable with an H∞ performance index γ, if there exist positive definite matrices Xi, Y, S, ¯Qi, ¯Ri, ¯H and ¯V (i=1,2) with appropriate dimensions such that
where
The control coefficient matrix of the observer-based controller is shown by: K=YX2−1, L=S¯X−12, with CX2=¯X2C.
Proof. Set P=[P10∗P2] and define X=P−1=[X10∗X2], ¯Qi=XTQiX, ¯Ri=XTRiX (i=1,2), ¯H=XTHX, ¯V=X2TVX2, Y=KX2, S=L¯X2. For X2=W[X210∗X22]WT, on the basis of [35], there exist ¯X2=MNX22N−1MT such that CX2=¯X2C.
Define Φ=diag{X,X,X,X,X2,I,I,I,I,I}, then pre- and postmultiply Φ and its transpose on both sides of (3.1). It is easy to know that −X¯R−1iX≤¯Ri−2X,(i=1,2), −X2¯V−1X2≤¯V−2X2. Finally, we can conclude that (3.1) is a sufficient condition to guarantee (3.6) holds. The proof is accomplished.
Remark 3. The power system under investigation is a complex continuous system, whose stabilization is further complicated by disturbances such as wind power generation, making the calculation of controller parameters a challenging task. Lyapunov theory is well used to facilitate analysis and predict system behavior, especially for complex systems.
4.
Simulation results
In this part, we consider a simulation example for a two-area power system and demonstrate the usefulness of this method. The parameter values of system (2.15) are shown in Table 2 [25].
Set σ=0.01, dM=0.1, dm=0.02 and the sampling period is h=0.05. The initial condition, in this simulation analysis, is given by ˜x(0)=[0.0010.001…0.001]. Next, by solving Theorem 2, the control gain K and the observer gain L are given by
Meanwhile, H∞ performance index γ=15.4285. Here we set the disturbance ω(t) occurs at every sampling instant as ω(t)=√0.161+t2, and the probability that the system suffers from an effective DoS is 0.3.
In this simulation, we analyze the effects of a DoS attack on system dynamics and control responses.
Figure 2 illustrates DoS attack signals from 0−10s denoted by τ(ikh), highlighting the attack's temporal characteristics and intervals of disrupted transmission.
The frequency deviation Δfi in the affected region, as depicted in Figure 3, shows fluctuations due to the DoS attack. However, it gradually stabilizes and tends toward zero, indicating a system tendency to regain frequency balance over time. This response underscores the system's capacity for frequency recovery even under compromised conditions.
Figure 4 presents the output power deviation ΔPaci of the ACs in the region under DoS attack. Notably, the fluctuations are contained within a narrow range, remaining below 0.1, demonstrating a limited impact on the output power deviation of the ACs. This outcome suggests that the control strategy maintains a relatively stable response in the face of attack-induced disturbances.
The area control error ACEi in Figure 5 provides insights into area control performance under the DoS attack.
Meanwhile, Figure 6 depicts the error between the observer state and the system state, revealing a similar pattern between them. While exhibiting oscillatory behavior, the rapid reduction of the error, however, is not completely zero due to the presence of perturbations. This suggests that the observer maintains some accuracy despite the attacks.
The timing of event triggers, illustrated in Figure 7, reveals that the maximum trigger interval significantly exceeds the sampling period. This long trigger interval shows the efficacy of the proposed ETM in maintaining system stability and efficiency under DoS conditions. The extended trigger interval also highlights the ETM's capability to manage communication load, triggering transmissions only when essential and thus enhancing safety and stability in the presence of network-based attacks.
5.
Conclusions
In this paper, we have studied the problem of LFC with ACs under DoS attack considering ETM in network environment. When constructing the system model, we have considered the randomness of wind power generation and photovoltaic power generation and have also added the ACs to participate in the frequency regulation. In order to improve the utilization efficiency of network resources while resisting DoS attacks, an ETM has been proposed. During DoS attacks, system stability criteria and control design methods have been derived using H∞ stability theory and LMI techniques for co-designing controller and observer gains. Finally, the proposed control strategy has been applied to the two-area smart grid, and the results have shown that the control method is effective.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work was supported by Science and Technology Project of State Grid Anhui Electric Power Co., Ltd. (Grant No. 521205240016).
Conflict of interest
The authors declare there are no conflicts of interest.









 DownLoad:
DownLoad: