1. Introduction
Recently, there has been much discussion about the potential for bioenergy production from forest-derived biomass. For example, forests could provide important sources of cellulosic feedstocks for second-generation liquid biofuels [1]. In addition, wood pellets from forest biomass may be a critical part of the global renewable electricity portfolio in the near future [2]. Whether for liquid biofuels or wood pellets, forest biomass may lower some ecological impacts compared with crop-based biofuel feedstocks, which are usually grown in monocultures [3]. However, compared with energy sources such as coaland petroleum, cellulosic biofuels and electricity from biomass require more land per unit of energy [4]. Therefore, widespread forest biomass production for bioenergy has the potential to cause substantial land-use change, and thus impact landscapes, habitats, and ecosystems [5, 6, 7].
In the southeastern U.S., biomass from forests could be an important source of bioenergy [8, 9, 10]. Forest biomass production in the region would likely lead to increased conversion of naturally-regenerating forests and agricultural lands to intensively managed forests, elevated thinning and harvest rates in all forests, and increased use of forest residues such as small trees and branches [9].While several studies have investigated ecological impacts of these types of changes at local scales, the landscape impacts of large-scale biomass production has been identified as a critical research need in the Southeast and beyond [3, 10, 11]. Investigating landscape impacts and tradeoffs using plausible future scenarios of biomass production over time is a particularly important research need [12]. In the Southeast, future scenarios that incorporate forest economics will be especially critical because factors like demand for forest products and forest land are key drivers of land change there [13, 14]. Here, we model landscape dynamics of potential forest biomass production scenarios in North Carolina using state-and -transition simulation models (STSMs), along with an economics-based timber supply model.
Several features of STSMs make them ideal for simulating land conversion and elevated management that are likely under alternative biomass production scenarios. In STSMs, vegetation stages, land-use types, and transitions among them, whether due to ecological or anthropogenic drivers, are represented by discrete model components much like Markov models or conceptual state-and -transition models [15, 16]. But, additional features in STSMs also facilitate the simulation of transitions such as land-use change or management regimes that can change over time [15]. Furthermore, unlike other simulation models built exclusively for forest vegetation types, the flexibility of STSMs allows representation of any vegetation or anthropogenic land-use type. For these reasons, STSMs have become increasingly popular tools for investigating scenarios of landscape and forest dynamics [17, 18, 19, 20] and make them well-suited for our study.
Our objective in this study was to link STSMs with an economics-based timber supply model to examine landscape dynamics in North Carolina (NC) through 2050 under two scenarios of forest biomass production along with a baseline, or business-as-usual scenario. The SubRegional Timber Supply (SRTS) model [21, 22], was used to incorporate the important economic drivers of forest land change and management into STSMs. Specifically, our objectives were to: (1) simulate potential future landscape dynamics in NC using STSMs based on output from a timber supply model, and (2) examine how alternative simulated scenarios of forest biomass production are likely to affect landscape dynamics in NC. To address our first objective, we used SRTS to generate annual target areas for land-use conversion and forest management transitions, then input these targets into an STSM and examined how closely target areas from SRTS matched areas simulated by the STSM. To address our second objective, we compared the three scenarios in terms of areas of vegetation and land-use types in NC through time, and annual areas experiencing transitions such as forest disturbance and management. The result is a new application of STSMs for underst and ing potential landscape dynamics due to bioenergy production.
2. Materials and Methods
We linked timber supply and state-and -transition simulation models (STSMs) to examine the effects of forest biomass production for bioenergy in NC using the following approach. First, we used supply chain analysis and existing literature to determine how much demand for forest biomass might be expected in the future. We developed two scenarios of forest biomass production to fit that demand , along with a third, baseline, or business-as-usual scenario. Second, we developed a series of state-and -transition model pathways in the STSM software platform ST-Sim to represent ecological dynamics, forest management, and land-use change within and among vegetation and land-use types across the state. Third, we used recent land cover and other spatial data to determine the composition of vegetation (forest and non-forest) and land-use types across North Carolina in the year 2010. Fourth, we used the SubRegional Timber Supply (SRTS) model to project areas of forest that are thinned or harvested under each scenario, along with changes in the area of major forest types, urban lands, and agricultural lands across four regions of the state. Fifth, we input the SRTS projections, and initial conditions into ST-Sim to project changes in land use and vegetation from 2011 through 2050.
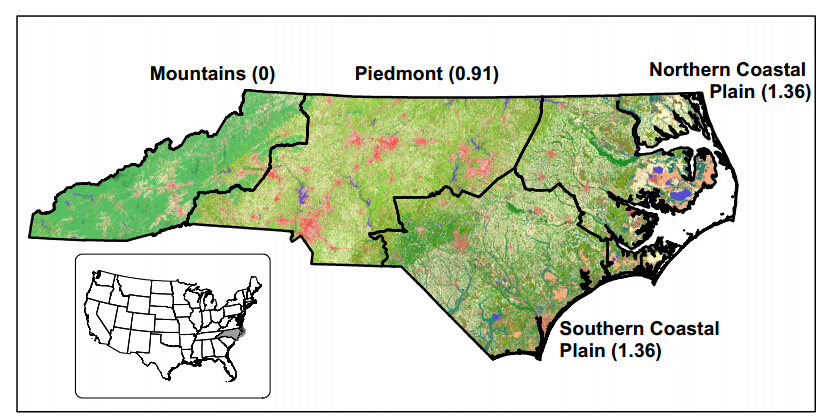
For modeling, we divided NC into four regions that are analogous to those used by the USDA Forest Service’s Forest Inventory and Analysis (FIA) program (Figure 1): groups of counties corresponding to the Northern Coastal Plain, Southern Coastal Plain, Piedmont and Mountains. The SRTS model is designed to work at regional extents, and these are regions of similar land use and vegetation, with relatively homogenous drivers of change (see below). In addition, the regional domains allowed reasonably fast simulation by the STSMs.
2.1. Study area: North Carolina
The state of NC has three distinct physiographic regions: the Coastal Plain, Piedmont, and Mountains. Major forested vegetation types across the state include longleaf pine ecosystems and oak-pine forests (Table 1). The majority (89%) of the state is privately owned, with most large public areas occurring in the Mountains and on the outer Coastal Plain [23]. Planted loblolly pine (Pinus taeda) plantations make up 8% of the state, and much of that area (58%) is in the Coastal Plain region. Agricultural land uses, including row crops and pastures, cover 23% of the state’s area, most of which is in the Coastal Plain (56%) and Piedmont (35%). Urban areas occur across the state, making up 11% of the land use statewide. The majority (52%) of urban land is in the Piedmont region, which contains the state’s largest urban areas, including Charlotte and the Raleigh-Durham area. The Piedmont region is also projected to see the highest future rate of urbanization [24]. The state contains some of the most highly-diverse ecosystems in the world, and in particular, the Coastal Plain occurs in a global biodiversity hotspot [25]. Therefore, it is important to determine how biomass production will affect landscapes in NC. To meet future energy demand in NC, forest bio mass will likely be produced from the major forest types, including managed and non-managed pine and hardwood forests, which are already present on the landscape, and are used to produce other forest-based products such as timber and paper products.
Table 1. Information about the land-use and vegetation types modeled and their initial extents.
| Name | Initial area (ha) | % of total extent | SRTS general forest typea | General type | Model sourceb | |
| Appalachian Hemlock-Hardwood Forest | 8, 927 | 0.09% | Mixed pine hardwood | Forest | LANDFIRE | |
| Atlantic Coastal Plain Central Fresh-Oligohaline Tidal Marsh | 4, 036 | 0.04% | NA | Wetland | LANDFIRE | |
| Atlantic Coastal Plain Central Maritime Forest | 5, 277 | 0.05% | NA | Forest | LANDFIRE | |
| Atlantic Coastal Plain Central Salt and Brackish Tidal Marsh | 14, 142 | 0.14% | NA | Wetland | LANDFIRE | |
| Atlantic Coastal Plain Clay-Based Carolina Bay Forested Wetland | 3, 581 | 0.04% | NA | Forest | LANDFIRE | |
| Atlantic Coastal Plain Dry and Dry-Mesic Oak Forest | 387, 324 | 3.87% | Upland hardwood | Forest | LANDFIRE | |
| Atlantic Coastal Plain Embayed Region Tidal Freshwater Marsh | 2, 639 | 0.03% | NA | Wetland | LANDFIRE | |
| Atlantic Coastal Plain Embayed Region Tidal Salt and Brackish Marsh | 33, 485 | 0.33% | NA | Wetland | LANDFIRE | |
| Atlantic Coastal Plain Fall-line S and hills Longleaf Pine Woodland | 137, 623 | 1.37% | Natural pine | Forest | LANDFIRE | |
| Atlantic Coastal Plain Mesic Hardwood and Mixed Forest | 38, 982 | 0.39% | Upland hardwood | Forest | LANDFIRE | |
| Atlantic Coastal Plain Nonriverine Swamp and Wet Hardwood Forest | 123, 793 | 1.24% | NA | Forest | LANDFIRE | |
| Atlantic Coastal Plain Northern Basin Swamp and Wet Hardwood Forest | 8, 451 | 0.08% | Lowland hardwood | Forest | LANDFIRE | |
| Atlantic Coastal Plain Northern Dune and Maritime Grassland | 232 | 0.00% | NA | Wetland | LANDFIRE | |
| Atlantic Coastal Plain Northern Fresh and Oligohaline Tidal Marsh | 216 | 0.00% | NA | Wetland | LANDFIRE | |
| Atlantic Coastal Plain Northern Maritime Forest | 435 | 0.00% | NA | Forest | LANDFIRE | |
| Atlantic Coastal Plain Northern Tidal Salt Marsh | 7, 165 | 0.07% | NA | Wetland | LANDFIRE | |
| Atlantic Coastal Plain Northern Tidal Wooded Swamp | 711 | 0.01% | Lowland hardwood | Forest | LANDFIRE | |
| Atlantic Coastal Plain Peatland Pocosin | 247, 828 | 2.47% | NA | Forest | LANDFIRE | |
| Atlantic Coastal Plain Small Blackwater River Floodplain Forest | 268, 943 | 2.68% | Lowland hardwood | Forest | LANDFIRE | |
| Atlantic Coastal Plain Small Blackwater Stream Floodplain Forest | 129, 921 | 1.30% | Lowland hardwood | Forest | LANDFIRE | |
| Atlantic Coastal Plain Small Brownwater Floodplain Forest | 150 | 0.00% | Lowland hardwood | Forest | LANDFIRE | |
| Atlantic Coastal Plain Small Brownwater River Floodplain Forest | 100, 975 | 1.01% | Lowland hardwood | Forest | LANDFIRE | |
| Atlantic Coastal Plain Southern Dune and Maritime Grassland | 3, 392 | 0.03% | NA | Grass/shrub | LANDFIRE | |
| Atlantic Coastal Plain Southern Tidal Wooded Swamp | 4, 843 | 0.05% | Lowland hardwood | Forest | LANDFIRE | |
| Atlantic Coastal Plain Streamhead Seepage Swamp, Pocosin, and Baygall | 2, 233 | 0.02% | NA | Forest | LANDFIRE | |
| Atlantic Coastal Plain Upland Longleaf Pine Woodland | 676, 615 | 6.75% | Natural pine | Forest | LANDFIRE | |
| Centralandsouthern Appalachian Montane Oak Forest | 40, 591 | 0.41% | Upland hardwood | Forest | LANDFIRE | |
| Centralandsouthern Appalachian Northern Hardwood Forest | 15, 132 | 0.15% | Upland hardwood | Forest | LANDFIRE | |
| Centralandsouthern Appalachian Spruce-Fir Forest | 199 | 0.00% | Natural pine | Forest | LANDFIRE | |
| Central Atlantic Coastal Plain Wet Longleaf Pine Savanna and Flatwoods | 45, 846 | 0.46% | Natural pine | Forest | LANDFIRE | |
| Pasture/Hay | 1, 484, 970 | 14.82% | NA | Agriculture | New model | |
| Planted Pine -Private | 1, 068, 082 | 10.66% | Planted pine | Forest | New model | |
| Row Crop | 1, 623, 992 | 16.21% | NA | Agriculture | New model | |
| South-Central Interior Large Floodplain | 281 | 0.00% | Lowland hardwood | Forest | LANDFIRE | |
| South-Central Interior Small Stream and Riparian | 2, 927 | 0.03% | Lowland hardwood | Forest | LANDFIRE | |
| Southeastern Interior Longleaf Pine Woodland | 88 | 0.00% | Natural pine | Forest | LANDFIRE | |
| Southern and Central Appalachian Cove Forest | 41, 855 | 0.42% | Upland hardwood | Forest | LANDFIRE | |
| Southern and Central Appalachian Oak Forest | 545, 218 | 5.44% | Upland hardwood | Forest | LANDFIRE | |
| Southern and Central Appalachian Oak Forest -Xeric | 306, 289 | 3.06% | Upland hardwood | Forest | LANDFIRE | |
| Southern Appalachian Grass and Shrub Bald | 138 | 0.00% | NA | Grass/shrub | LANDFIRE | |
| Southern Appalachian Low Mountain Pine Forest | 23, 445 | 0.23% | Natural pine | Forest | LANDFIRE | |
| Southern Appalachian Montane Pine Forest and Woodland | 694 | 0.01% | Natural pine | Forest | LANDFIRE | |
| Southern Piedmont Dry Oak Pine Forest | 2, 065, 837 | 20.62% | Mixed pine hardwood, natural pinec | Forest | LANDFIRE | |
| Southern Piedmont Large Floodplain Forest | 5, 223 | 0.05% | Lowland hardwood | Forest | LANDFIRE | |
| Southern Piedmont Mesic Forest | 748 | 0.01% | Upland hardwood | Forest | LANDFIRE | |
| Southern Piedmont Small Floodplain and Riparian Forest | 42, 428 | 0.42% | Lowland hardwood | Forest | LANDFIRE | |
| Southern Ridge and Valley Dry Calcareous Forest -Pine | 7 | 0.00% | Natural pine | Forest | LANDFIRE | |
| Urband | 466, 828 | 4.66% | NA | Urban | New model | |
| Total | 9, 992, 735 | ‒ | ‒ | ‒ | ‒ | |
a Non-forested vegetation types as well as forest types that are unlikely to be managed for biomass were excluded from SRTS. See text for more details.
b LANDFIRE indicates that the modified from a model developed for the same system by LANDFIRE (http://www.land fire.gov).
c In the Southern Piedmont Dry Oak Pine Forest model, the state classes corresponding to pine-dominated conditions were treated as natural pine forest. All others were mixed pine.
d Urban land in initial conditions did not include land that was classified developed but with low intensity or open space. |
2.2. Scenarios of future demand for forest biomass
North Carolina has the potential for substantial forest-based biomass demand for bioenergy. The state is the only one in the southeastern U.S. with a renewable energy portfolio st and ard and , until recent changes in state policy, had a biofuel target of 10% of liquid transportation fuels from locally produced biofuels [27]. Such demand could be met from forest biomass, or from agricultural crops such as switchgrass or sweet sorghum. In addition to biofuels, existing or announced wood pellet plants in NC could consume 3.45 million green tonnes (3.8 million green short tons) of forest biomass annually [28]. For this study we examined the impact of producing 3.63 million green tonnes (4.0 million green short tons) of wood-based bioenergy annually, which would meet up to 29% of the biofuels target (see Supplementary Material for biomass to ethanol conversion) or 100% of wood pellet demand .
We developed two scenarios that incorporated annual production of 3.63 million green tonnes of biomass for bioenergy but varied in the degree to which forest residues would be removed and compared those to a business-as-usual scenario in which no biomass was produced for bioenergy. Forest residues include small trees, tree tops, rough wood, rotten logs and snags that cannot be used in a conventional lumber mill or other processing facility. Because forest residues play important ecological roles, such as providing habitat for wildlife, promoting biodiversity, and as sources of soil nutrients, the degree to which they are harvested could have major impacts on forest ecology and wildlife habitat [11, 29, 30, 31]. Residues can be used to produce some forms of bioenergy such as biofuels, but only certain types of residues such as small trees can be used to produce wood pellets. As a result, the degree of harvest of residues is a major uncertainty in any future production of forest biomass, and may range from no residue use to over 50% of residues used. Therefore, to ensure we were within the potential range of residue use, our two biomass scenarios, respectively, assumed that either 20% or 40% of forest residues would be removed.
In our two biomass scenarios, production varied by region of the state (Figure 1). Because of the existing forestry infrastructure in the Coastal Plain, we assumed that region is likely to have the greatest capacity to increase production, and we assumed that 1.36 million green tonnes (1.5 million green short tons) would be produced annually in each of the two Coastal Plain regions. The Piedmont region has some infrastructure, and thus has the capacity to increase production a moderate amount, and we assumed 0.9 green tonnes (1.0 million green short tons) of annual biomass production there. We expect no increase in forest biomass production in the Mountains because little forest harvest is done in that region.
2.3. State-and -transition simulation modeland pathways (ST-Sim)
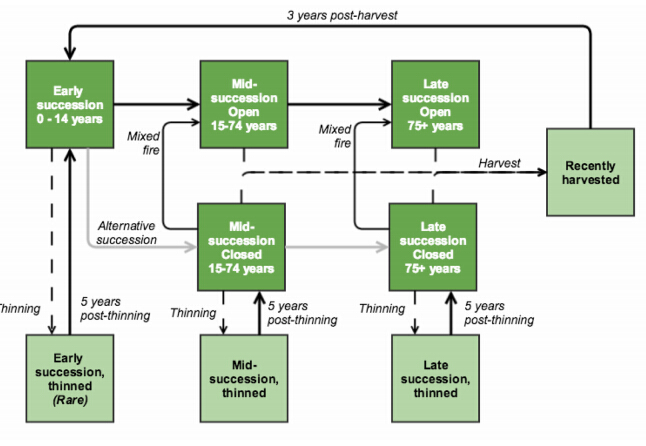
To develop state-and -transition pathways and run the STSM, we used ST-Sim software, version 2.3.0 [32]. ST-Sim is similar to, and builds upon, other STSMs, including VDDT and Path [15]. In ST-Sim, a pathway is developed for each vegetation or land-use type (see Figure 2 for an example), which defines discrete “state classes” and transitions among state classes. State classes are defined for each vegetation or land-use type based on characteristics such as successional stage and canopy cover. Transitions include ecological succession; disturbances such as wildfire; forest management, including thinning and harvest; and conversion from one land-use or vegetation type to another. Initial conditions define the starting point for the model, and the simulation proceeds from the initial landscape on an annual time step. At each time step, transitions among state classes occur in a semi-Markov framework, based on rules and probabilities set in the state-and -transition models. Limits to the total amount of forest management and land conversion in any given time step are set by time series called “transition targets” that come from SRTS outputs. Therefore, there are three main types of inputs to ST-Sim: (1) state-and -transition model pathways for each of the vegetation or land-use types in NC, (2) a table describing initial landscape conditions, including the areas of NC in each state class for all vegetation and land-use types, and (3) time series of annual areas to be thinned, harvested, or converted, from SRTS model output. We discuss (1) below, and discuss (2) and (3) in subsequent sections. ST-Sim can be run spatially or aspatially. Here we are running the model aspatially because we are focused on linking the SRTS and ST-Sim models, and examining differences among scenarios in terms of changes in areal extents of vegetation and land use types.
We developed state-and -transition model pathways for 49 vegetation and land-use types in NC (Table 1). For most vegetation types, the pathways we used were modified from those developed for the LANDFIRE project (available at http://www.land fire.gov) [33]. In those pathways, states are defined for each vegetation type in terms of their successional stage (early, mid-or late succession), and their canopy cover (open or closed canopy). Transitions among state classes include ecological succession, which is deterministic after a pre-defined number of time steps, and disturbance events, including wildfires, which are probabilistic. In most cases, one LANDFIRE model pathway represented a single ecological system, as defined by NatureServe [34], but in some cases for wetland vegetation, a LANDFIRE model pathway represented a group of ecological systems. The LANDFIRE models reflect successionaland disturbance dynamics in those systems that were likely present prior to European settlement. Each pathway is accompanied by written documentation describing the structural characteristics of each state class, including the canopy cover for each state class. A few other ecological systems occurred in NC but were not included here. These were systems that occurred in small patches, or were naturally barren or sparsely vegetated and were therefore not expected to contribute to landscape dynamics.
We modified the LANDFIRE model pathways in several important ways to reflect current conditions and forest biomass production scenarios. First, we reduced wildfire probabilities for every vegetation type by 93% to reflect contemporary fire suppression in the Southeast following our other recent work [35] by adding a multiplier of 0.07 for every wildfire transition in all pathways. For models of forested vegetation types, we added states and transitions to represent harvest and thinning (See Figure 2 for an example, and Supplementary Material for all model state classes and transitions). In those pathways, a thinning transition was added to every state class that had a closed canopy condition or represented early succession. We also added state classes that represented early, mid-, or late-succession “recently-thinned” conditions. St and s undergoing thinning in a given successional stage transitioned to the analogous “recently thinned” state class, in which canopy cover was reduced by 50% from pre-thinning conditions. St and s stayed in this state class for five years following thinning before transitioning back to the pre-thinned state class. In addition, a harvest transition was added to every state class, which could convert a st and to a “recently harvested” state class. Within two years of harvest, a st and was eligible to be converted to planted pine forest or row crop; otherwise, after three years, the st and transitioned back to the early succession state class of the same forest type it previously occupied. For every forest type, annual areas undergoing harvest and thinning were constrained with transiti on targets from the SRTS model, and while early succession state classes were eligible for harvest and thinning, these transitions rarely occurred during simulation due to age constraints from SRTS (see below). Finally, we added transitions to every state class in every modified LANDFIRE model pathway to represent conversion to urbanization (see below for probabilities).
In addition to modifying LANDFIRE model pathways, we created model pathways to reflect anthropogenic land uses that were not modeled by LANDFIRE, including planted pine, urban land , row crop, and pasture (see Supplementary Material for all model state classes and transitions). All of the new pathways for anthropogenic land uses consisted of a single state class, except planted pine. The planted pine model pathway consisted of two portions, a “managed” portion and a “non-stocked” portion. The planted portion represented st and s that had been planted and actively managed for forest products (either conventional uses such as timber, or biomass). The non-stocked portion represented areas that had been planted and managed for forest products in the past, or were in agriculture, but were naturally regenerating after harvest. In addition, conversion of agricultural lands to natural vegetation transitioned to the early succession state class of the non-stocked model. As mentioned above, the recently harvested state class in every forest vegetation type was eligible to be converted to row crop.
Finally, for all state classes in every vegetation and land-use model pathway, we added a transition to urbanization, with probabilities that varied by region according to a summary of recent urbanization projections [24] (0.0023 for state classes in the Southern Coastal Plain, 0.0012 for the Northern Coastal Plain, 0.0152 for the Piedmont, and 0.0079 for the Mountains).
2.4. Initial conditions
The initial condition file required for using the state-and -transition models in NC was a table of the areas of each land cover class, along with areas and ages (in years) by vegetation type and state class. To develop this table, we used recent land cover and other environmental spatial data. The Southeast GAP 2001 land cover map [26] was used to distinguish the 49 land cover and vegetation types. The vegetation types for which we did not develop state-and -transition model pathways were not included. The extent of urban lands was updated to reflect 2010 conditions based on recent data [24].Within each vegetation type, we further distinguished state classes based on canopy cover and successional stage. We used LANDFIRE 2008 succession class data (s-class) [36] to assign a successional stage and canopy cover (early mid, or late succession; open or closed canopy) for most vegetation types. However, inspection of the s-class data for the Southern Piedmont Dry Oak-Pine Forest vegetation type, which made up 20.6% of the initial mapped area of NC (Table 1), indicated that the open canopy con dition was overrepresented in the data for the mid-succession stage of that vegetation type. The majority of the mid-succession stage was classified as open canopy in the s-class data, while in reality most oak-pine forests in the Piedmont have a relatively closed canopy. Therefore, we used canopy cover data from the National land Cover Database [37] to distinguish open and closed canopy states for that vegetation type, according to the LANDFIRE model description [38]. For all vegetation types, we assigned ages to match the distribution of ages in forest types according to data from the USDA Forest Service Forest Inventory and Analysis (FIA) database [39].Here, we used data from the FIA survey for forest plots in NC that was closest to our initial year (2010).
To compile our initial conditions input into ST-Sim, for each of the four modeled regions of NC, we summarized the areas of vegetation types by successional stage, canopy cover, and age. We also summarized areas of each urban and agriculture land-use type. We assumed lands under protection for conservation would not be subject to management for biomass, so we used the U.S. Protected Areas Database [23] to exclude those lands. See Supplementary Material for ST-Sim initial conditions. For SRTS modeling, we further summarized the land uses, vegetation types and ages using a crosswalk with five general forest types, agriculture, and urban land (see text below, and Table 1). Non-forest vegetation such as shrubland , wetland , and grassland was not included in SRTS.
2.5. Timber supply modeling (SRTS)
In order to simulate forest management and land-use change under alternative scenarios of forest biomass production in ST-Sim, we required time series of areal amounts of forest types undergoing management (harvest or thinning) and land-use conversion. Determining the effects of biomass demand on forests requires demand assumptions for the full range of forest products, including traditional small (pulpwood) and large (sawlogs) roundwood. Except for logging residues, these products will compete with bioenergy. The resulting price effects can lead to “displacement” of existing uses or “leakage” of demand to other regions. Therefore, the effects of biomass production on land use and forest management (thinning and harvesting) will not be additive. To incorporate that non-additivity, or “displacement” of other forest products, as well as baseline production, we used SRTS, which has been used in assessments of forest resources in the South and beyond [21, 22]
The SRTS model operates on an annual time step and combines economic resource allocation with biological growth to link timber markets (price and harvest for a range of timber products) with forest dynamics. At each time step, the model simulates the impact of exogenous demand scenarios on the areas of general forest types in 5-year age classes that are harvested or thinned, along with the total areas of those forest types, and total areas of agriculturaland urban land . For each region (group of counties) modeled, the forest inventory is adjusted annually from the initial conditions by adding net growth and subtracting the estimated harvest. The interactions between forest and agricultural land is driven by land rents, which include net income from forest harvest [14, 40]. In SRTS, annual areas of each forest and land-use type are determined based on an index of timber prices from the endogenous market model combined with a response surface of agriculturaland forest land prices from a recent land-use model [41]updated with the most recent land use data [42]. In this study we used recent urbanization projections [24] to define transitions from rural to urban land . Rural land is allocated between agriculturaland forest land based on relative economic returns each year.
For SRTS modeling, we used the same initial conditions file described above, but aggregated vegetation types into general forest types, including one planted pine type and four natural forest types, and 5-year age classes. Because SRTS models forest change only, some vegetation types (such as marshes and beach vegetation) were excluded from SRTS modeling. In addition, some forest vegetation types were also excluded from SRTS because they are unlikely to undergo intensive management for biomass. Such is the case for maritime forest types, which exist in small patches on s and y soils, and have low productivity. This meant that harvest, thinning, and agriculturaland urban land-use conversion for these vegetation types were not included in SRTS or ST-Sim modeling. We believe this is reasonable because these vegetation types are not likely to be used for biomass. In addition, many of these types are protected from land conversion (e.g. beach dunes) or are wetland vegetation, which has a low probability of conversion in the urbanization model [24].
When running SRTS models, we assumed in all scenarios that empirical demand for all forest products except pine sawtimber would increase 0.5% per year over recent FIA plot data throughout the simulation period. Because the recent recession greatly affected housing starts, and pine sawtimber is used for house construction, we adjusted pine sawtimber during the initial years of the simulation to reflect recession recovery. Pine sawtimber demand was increased by 3% per year from 2011-2014, by 1% per year from 2015-2019, and by 0.5% per year thereafter. All else was held constant in the baseline scenario. For the two scenarios that included forest biomass, we wanted to simulate the effects of an increase in biomass in the relatively near future, but realized that demand would take some time to reach target levels. Therefore, we increased demand gradually in these scenarios starting in 2015 until it reached the target demand in 2019 (Figure 1). demand was then held constant until the end of the projection. In these scenarios for a given region, we assumed the forest types used for biomass and forest logging residues would be the same as the mix of forest trees harvested. Depending on the scenario, up to 20% or 40% of available logging residues were used for both hardwood and pine forest types. The result of SRTS for each region and modeled scenario included two types of annual time series projections: (1) the areas thinned and harvested for the five general forest types and by age class, and (2) the total areas in natural forest, planted pine forest, agriculture, and urban land areas over time. These were used as input to ST-Sim.
2.6. Linking SRTS output with ST-Sim and running state-and -transition simulations
Before input into ST-Sim, the two SRTS outputs for each scenario and region modeled were manipulated to produce annual time series transition targets for land-use conversion and forest management. For the first output, annual areas of thinning and harvest by forest type and age class, the time series were smoothed by averaging over a five-year moving window because SRTS output values showed a high level of interannual variation, which is likely unrealistic.
We converted the second SRTS output, total areas of forest and land-use type by year, into annual transition targets for conversion among land-use types, with the exception of conversion of all types to urbanization, which we had data for from a previous study [24]. To do so, for a given land-use or forest type, we calculated the difference between the total area in a given year and the area for the previous year. We then removed any conversion to urban in the SRTS output by assuming that loss of all land-use types to urban from one year to the next was proportional to the relative areas of those land-use types. Thus, for example, if twice as much forest existed as agriculture, forest loss contributed twice as much area to urbanization as agriculture contributed. We then used a similar approach to compare the remaining (non-urbanization) changes in forest types and agriculture. We thus calculated a set of time series of areas converted among agriculture, planted pine forest, and natural forest types. We also averaged these time series over a five-year moving window. The result was transition targets for conversion among natural forest, and agricultural land uses. Note that because SRTS output provides annual areas that remain in each land-use type each year, the resulting transition targets capture only the net changes among land-use types for a given region. In reality, the annual areas in each land-use type are the result of conversion to and from each type. For example, a net increase in planted pine forest may be the result of conversion from agriculture, but in reality some conversion of planted pine to agriculture may have also occurred. We do not capture these gross changes.
The transition targets were applied to transitions in ST-Sim based on the crosswalk between the ST-Sim and SRTS land-use and vegetation types (Table 1), and were constrained to state classes with the appropriate ages. For example, a transition target area for thinning in mixed pine hardwood forest, ages 16‒20, in the Piedmont was applied to all ST-Sim vegetation types in that region that corresponded to mixed pine hardwood forest. Further, within those ST-Sim vegetation types, the targets were applied to state classes that correspond to ages 16-20. If multiple state classes overlapped the age range (i.e., if in this case, early succession lasted until age 17, and mid-succession began at age 18), the transition target was applied to both state classes. This meant that a single SRTS transition target was often applied to multiple ST-Sim vegetation types or state classes. The ST-Sim software accommodates this by distributing transition targets among systems based on the proportion of each vegetation type and age class on the landscape in a given time step. For example, if a target is to be split between two ST-Sim state classes, and one has twice as much area as the other, the total area thinned is divided in a ratio of 2:1 to meet the transition target for the given year.
2.7. Simulating landscape dynamics
We simulated changes within and among vegetation and land-use types over time in all four regions of NC using ST-Sim under the three future scenarios from 2011‒2050. For simulation, ST-Sim requires a total simulation area and number of simulation cells. We set the total simulation area to equal the total area in the initial conditions in each region, and set the number of simulation cells to be such that the cell size was approximately 10 ha. In other words, the number of cells was set to total landscape size (in ha) /10 ha. For each scenario and region, we ran 50 Monte Carlo iterations of the ST-Sim model. We chose 50 iterations to ensure outputs reflected the range of possible outcomes due to the stochastic aspects of ST-Sim, while maintaining reasonable model run times.
To address our first objective regarding linking ST-Sim and SRTS, for land-use transitions, harvest, and thinning, we examined the correspondence between annual SRTS targets matched annual transition areas in ST-Sim output. To address our second objective, we compared dynamics of major land uses and general vegetation types between the two bioenergy scenarios, and compared each to the baseline scenario. We illustrate differences in vegetation dynamics among scenarios using two example vegetation types: the Atlantic Coastal Plain Upland Longleaf Pine Woodland and planted pine forest.
3. Results
We modeled landscape dynamics across 9, 992, 735 hectares (999, 274 km2), or 79% of the land area in NC. lands that were barren or sparsely vegetated, as well as public lands, were not included in our simulations. The comparison of transition targets derived from SRTS output for land-use change, harvest, and thinning to ST-Sim modeled transitions indicated relatively close agreement for most transition types and scenarios (Table2). The annual area undergoing each land-use change transition generally differed by 5% or less from transition targets on average. In many cases, the difference was less than 2%. Some harvest and thinning transitions showed slightly higher average differences, with three transitions in planted pine forest types averaging more than 8% difference from transition targets. However, most harvest and thinning transitions also differed by less than 2% from annual targets.
Table 2. Average area (ha) undergoing harvest, thinning, and land-use transitionsa in ST-Sim, and the average difference between ST-Sim output and targets developed from SRTS.
| Transition | Baseline | Biomass, 20% residues | Biomass, 40% residues |
| ST-Sim avg. area | Difference (% of avg.) | ST-Sim avg. area | Difference (% of total) | ST-Sim avg. area | Difference (% of total) |
| Harvest, planted pine | 20, 534 | 2, 744 (13.4%) | 20, 976 | 1001 (4.8%) | 19, 550 | 1, 668 (8.5%) |
| Harvest, natural pine | 16, 125 | 129 (0.8%) | 18, 674 | 126 (0.7%) | 20, 126 | 137 (0.7%) |
| Harvest, mixed pine hardwood | 17, 131 | 1, 126 (6.6%) | 23, 972 | 1298 (5.4%) | 19, 255 | 1, 178 (6.1%) |
| Harvest, upland hardwood | 16, 933 | 68 (0.4%) | 19, 026 | 66 (0.3%) | 17, 184 | 72 (0.4%) |
| Harvest, lowland hardwood | 9, 354 | 31 (0.3%) | 13, 903 | 50 (0.4%) | 12, 652 | 43 (0.3%) |
| Thinning, planted pine | 35, 654 | 3, 347 (9.4%) | 46, 630 | 717 (1.5%) | 41, 895 | 1, 795 (4.3%) |
| Thinning, natural pine | 15, 086 | 66 (0.4%) | 14, 332 | 67 (0.5%) | 15, 250 | 58 (0.4%) |
| Thinning, mixed pine hardwood | 31, 051 | 1, 750 (5.6%) | 30, 136 | 1762 (5.8%) | 29, 675 | 1, 741 (5.9%) |
| Thinning, upland hardwood | 10, 140 | 37 (0.4%) | 9, 504 | 35 (0.4%) | 11, 096 | 37 (0.3%) |
| Thinning, lowland hardwood | 6, 638 | 33 (0.5%) | 8, 140 | 37 (0.5%) | 7, 505 | 33 (0.4%) |
| Ag to natural forest | 7, 984 | 29 (0.4%) | 9, 232 | 31 (0.3%) | 8, 241 | 25 (0.3%) |
| Ag to planted pine | 2, 521 | 14 (0.6%) | 5, 568 | 25 (0.4%) | 2, 818 | 17 (0.6%) |
| Natural forest to ag | 1, 984 | 100 (5.0%) | 2, 550 | 108 (4.2%) | 1, 967 | 101 (5.1%) |
| Planted pine to ag | 2, 143 | 27 (1.3%) | 1, 980 | 23 (1.2%) | 2, 157 | 25 (1.1%) |
| Planted pine to natural forest | 398 | 7 (1.8%) | 219 | 7 (3.1%) | 345 | 5 (1.4%) |
| a Although natural forest to planted pine transitions were possible in SRTS and ST-Sim, they did not occur. |
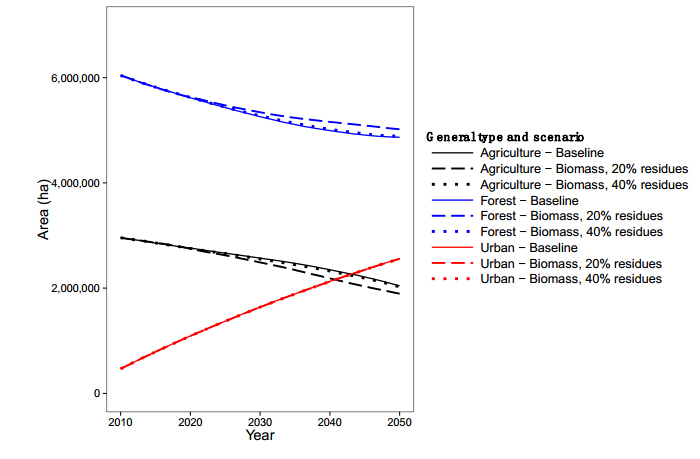
landscape dynamics, including areas of land-use and vegetation types on the landscape, as well as transitions due to thinning, harvest, and land-use change, showed some variation among the scenarios we simulated. In each case, dynamics were similar among scenarios up to the year 2015, when we added biomass production for bioenergy. In all scenarios over the simulation period across NC, the total areas of forest and agriculture decreased, while urban land increased (Figure 3). This result is not surprising, given the urbanization projections that were incorporated into these scenarios. However, there were important differences in these trends among scenarios. By the end of the simulation, the baseline scenario had the smallest area of forest and the largest area of agriculture remaining. Compared to the other two scenarios, the biomass scenario that incorporated 20% forest residue removal resulted in more forest and less agriculture on the landscape by the end of the period. The biomass scenario that incorporated 40% removal of forest residues resulted in an intermediate amount of agriculture and forest on the landscape compared with the other two scenarios, and the results were qualitatively similar to the baseline scenario. Because we simulated dynamics over time for over 200 state classes in all vegetation and land-use types, we are unable to show detailed results by state class over time for each, but we present the dynamics of change for two vegetation types below.
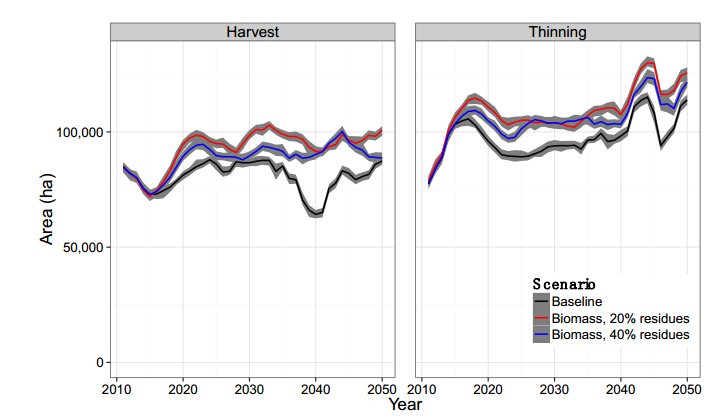
Overall, across the simulation period, the areas of forest thinned and harvested differed among scenarios (Figure 4). After the first few years of the simulation in which biomass production was gradually increased, there was a smaller area of forest harvested and thinned annually under the baseline scenario than under the two biomass scenarios. The biomass scenario that assumed only 20% of forest residues were removed resulted in the highest annual areas of thinning and harvest for most time steps. The scenario that assumed 40% residue removal resulted in areas of thinning and harvest that were intermediate between the other two scenarios for most time steps. There were some time steps in which either harvest or thinning amounts were highest for the scenario that incorporated 40% of residues, but there were no time steps in which both harvest and thinning were greater for the 40% residue scenario.
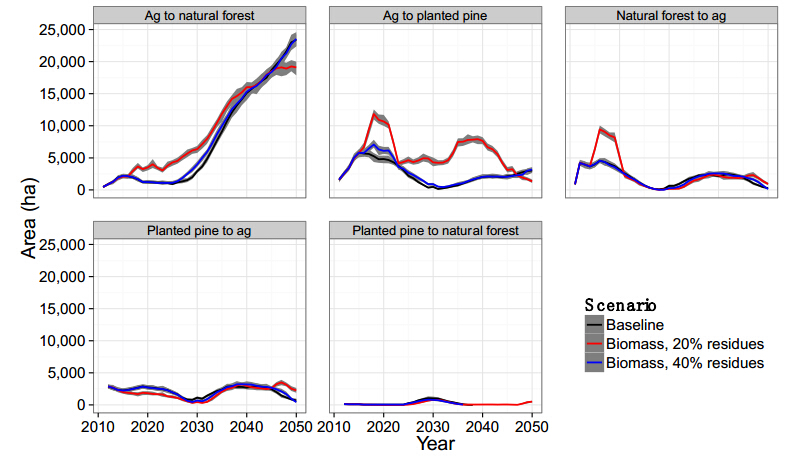
Trends in land-use change transitions across NC over time were similar for the baseline and 40% residue scenario, but differed slightly for the scenario that assumed 20% of residues (Figure 5). In particular, for most time steps in the simulation, the 20% residue scenario showed a larger area converted from agriculture to planted pine and natural forest than the other two scenarios. For a portion of the simulation period, that scenario also showed a higher area of natural forest converted to agriculture.
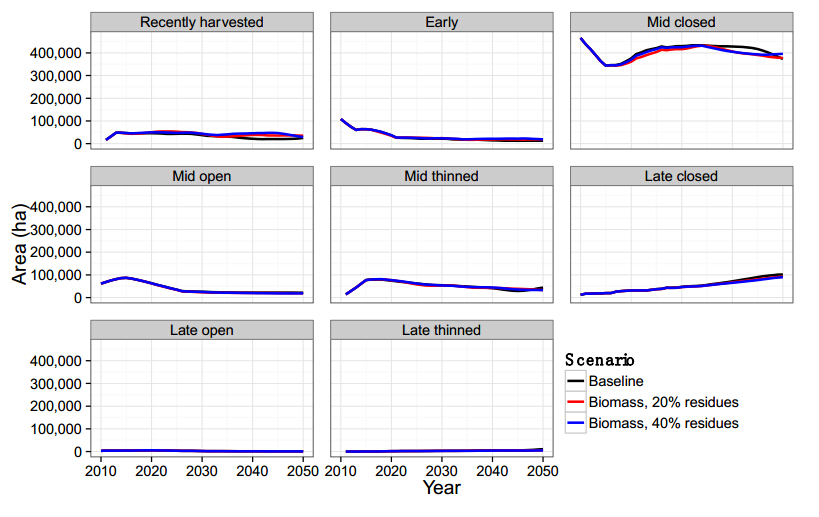
landscape dynamics results for the Atlantic Coastal Plain Upland Longleaf Pine Woodland were relatively similar among all scenarios (Figure 6). Areas in the early succession and mid-succession open canopy state classes decreased over time, while the late-succession closed canopy state class increased in area. Areas in the late-succession open and thinned state classes remained even over time, while the mid-succession thinned state class increased in area for the first five years, but then decreased. The only substantial differences among scenarios were in the recently harvested and mid-succession closed canopy states. The baseline scenario showed more area in mid-succession closed canopy and less in the recently harvested state compared with the other two scenarios in some years, due to the lower harvest rates for natural pine forest in that scenario (Table2).
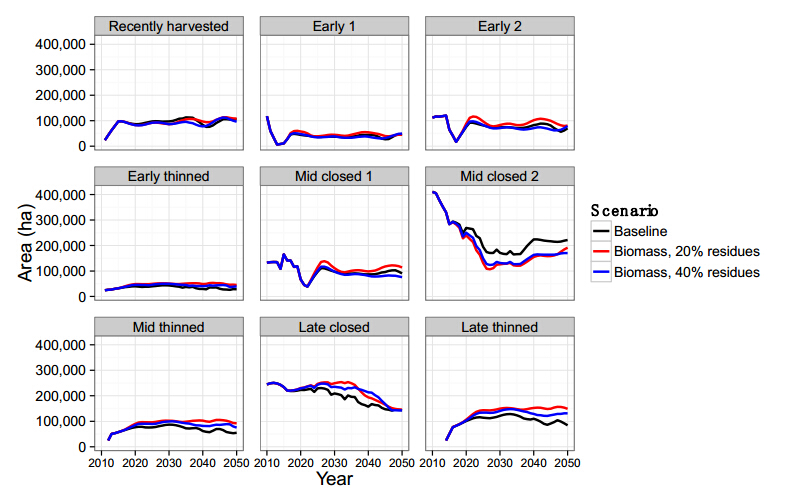
The dynamics of the state classes within the planted pine forest vegetation type over time show differences among scenarios (Figure 7). Compared to the baseline scenario, planted pine forests under the two biomass scenarios have less area in the two mid-succession closed canopy state classes, and a greater area in both late succession state classes. In addition, compared with the baseline scenario for most time steps in the simulation, the two biomass scenarios show a greater area of planted pine forest the mid-and late-succession recently thinned classes. The three scenarios show approximately the same areas in early succession state classes over time, but the biomass scenario that incorporates 20% residue removal has a slightly greater area than the other two scenarios.
4. Discussion
The future impacts and sustainability of bioenergy production on landscapes are uncertain, but depend on landscape dynamics [43]. To investigate the potential landscape impacts of bioenergy production, we simulated landscape dynamics under alternative forest biomass production scenarios in North Carolina. Results show that targets for land-use conversions as well as forest harvest and thinning under alternative scenarios produced by the economics based timber supply model SRTS can be used to inform landscape dynamics simulation in the state-and -transition simulation model (STSM) ST-Sim. The scenarios we modeled resulted in key differences in vegetation and land-use changes. While biomass scenarios led to more forest on the landscape, the scenarios also led to more recently harvested and thinned forest, and less closed canopy forest.
In most cases, areas undergoing forest and land-use transitions in the ST-Sim model output corresponded fairly well with transition targets set by SRTS. For all land-use change conversions, the ST-Sim model produced transition areas close to the SRTS target. In a few cases, for harvest and thinning, especially for planted pine forest, the ST-Sim transitions were different from the SRTS targets. Where these differences occurred, we believe they were likely due to differences between the two models in how they represent forest dynamics. For example, in SRTS, all land in each forest type is available to be thinned at any point in time, but in ST-Sim state-and -transition models, only the portion of forest in the closed canopy or early succession state classes was able to be thinned. Thus, compared with SRTS, the available forest area for thinning in any given year in ST-Sim could be lower, and target areas for thinning may not always be achievable. Because these differences were relatively minor in any given year, they would likely make little difference to overall forest dynamics and production of forest products and biomass. But, more tightly linking SRTS and ST-Sim could help ensure better agreement between the two models and facilitate ease of use. For example, dynamic coupling of the models so that they run simultaneously, so that for each time step, SRTS output serves as transition targets in ST-Sim, and areas in each forest vegetation type, state class, and land-use class from ST-Sim are aggregated and input back into SRTS for the following time step.
A comparison of general trends in land use among the three biomass scenarios show that while urban land area increased at the expense of forest and agricultural land in all scenarios, the amounts of agriculturaland forest land remaining by the end of the simulation period varied by scenario: the two biomass scenarios resulted in more forest and less agricultural land than the baseline scenario. The increased demand for forest products under the two biomass scenarios resulted in more conversion of forest to agriculture, and less conversion of agriculture to forest. This result is consistent with other studies that stress the importance of strong forest product markets for retaining forests on the landscape in the Southeast [13].
However, by enabling an examination of the trends within individual forest vegetation types, this study extends previous studies. Results indicate that increased harvest and thinning under the two biomass scenarios resulted in more intensively-managed forest on the landscape. Planted pine forest dynamics show more recently harvested and thinned forest, and less closed canopy forest on the landscape by the end of the simulation period under the biomass scenarios than under the baseline scenario. While differences were smaller for the Longleaf Pine Woodland , dynamics for that vegetation type also showed a slight increase in recently harvested forest at the expense of closed canopy forest. Therefore, while biomass scenarios may keep more forest on the landscape than a business-as-usual future, that forest may be more intensively managed.
This study also extends previous studies by examining landscape impacts of alternative residue removal scenarios. Differences between the two biomass scenarios show that assuming a higher rate of forest residue removal during harvest resulted in smaller areas of thinning, harvest, and some land-use changes than a lower residue removal rate. Therefore, it is clear that forest residues were able to meet some of the demand for biomass. In some cases, for some types of transitions such as conversion of agriculture to planted pine, the scenario with lower residue removal resulted in dynamics that were almost identical to the baseline scenario. This result suggests that an even higher rate of residue removal, such as 70‒80%, as recommended by some guidelines for liquid biofuels [29, 30], may not cause much, if any, difference in landscape dynamics compared with a baseline, non-bioenergy scenario.
A strength of this modeling effort linking SRTS and ST-Sim is the ability to incorporate temporal variation in annual areas of harvest and thinning. For example, toward the end of the simulation period, the area thinned under all scenarios decreased and then increased. Area harvested followed a similar, but opposite, trend for the same time period. These fluctuations reflect two aspects of the models. First, the SRTS and ST-Sim models both incorporate varying eligibility for harvest and thinning due to forest age. If a large area of forests is of a similar age and therefore becomes eligible for thinning or harvest all at once, fluctuations in harvest or thinning could be pronounced. In addition, harvest and thinning combine to meet the biomass targets in SRTS. So, when one of these management transitions decreases, an increase in the other is likely. By incorporating these temporal variations, we are able to go beyond recent modeling efforts that have assessed potential bioenergy impacts for the current landscape only [44].
While our scenarios provide insight into landscape-level changes due to forest biomass production, the local ecological effects of increased management intensity, including forest residue removal, under biomass scenarios may be positive or negative, depending on the ecological target, and should be explored further. For example, while removing forest residues lessens landscape effects, the practice may have negative local effects on amphibian species that nest in snags or down logs in some vegetation types [45], though effects may vary by species and vegetation type [46, 47]. In addition, forest harvest and thinning may have positive effects on some bird species that use early successional habitats or forests with reduced tree canopies but not on other species [47, 48, 49]. Furthermore, North Carolina contains several vegetation types with high diversity. Woodlands that make up the longleaf pine ecosystem have among the highest levels of plant richness per square meter of any ecosystem in the world [51] and the North American Coastal Plain, of which North Carolina’s Coastal Plain is a part, is rec ognized as a global biodiversity hotspot [25]. Therefore, any changes due to bioenergy production that result in forest conversion or more intense management have the potential to impact this biodiversity.
One caveat to our simulation results is that our models have not been fully validated by conducting historical simulations and testing outputs against observations. Full validation and model testing should be an important next step in the development of our modeling framework. However, our objective in this paper is to report on differences among biomass scenarios, which depend on scenarios of land conversion and management from SRTS. Importantly, SRTS is based on empirical observations from USDA Forest Service Forest Inventory and Analysis data. Therefore, we are confident in our conclusions about differences among the scenarios we simulated.
In addition to the further research already discussed, the STSMs presented here could be exp and ed to incorporate additional scenarios and realism. For example, the proximity of sites to an existing or planned facility that processes biomass into bioenergy may affect the likelihood of biomass harvest. Spatially explicit STSMs would allow the incorporation of mapped suitability surfaces for changes in production depending on geography or site characteristics. Furthermore, incorporating additional feedstocks for bioenergy, including so-called “purpose-grown crops” for biofuels, such as switchgrass and sweet sorghum, would allow investigation of the effects of a wider range of production scenarios.
5. Conclusion
Taken together, our results show the importance and utility of linking a forest economics model with an STSM to investigate landscape dynamics in response to alternative biomass production scenarios. The non-linear and variable trends of forest management and land-use conversions through time due to the interactions between successional dynamics, forest product markets, and demand for forest land would be difficult to determine without SRTS output. And the use of STSMs allowed us to investigate the dynamics of specific vegetation types and state classes, which other studies based on field data or static landscapes have not addressed.
Overall, landscape dynamics results show that compared with the baseline scenario, forest biomass production scenarios lead to more forest and , specifically, more intensively managed forest on the landscape by the end of the simulation. However, even a moderate harvest rate for forest residues dampens the effects of biomass production on landscape dynamics. These results suggest that on one h and , biomass production for bioenergy may have some landscape effects that could negatively impact species and ecosystems in the state. On the other h and , those impacts could be minimized by incorporating certain harvesting practices. Therefore, this research points to a future in which biomass has the potential to be produced sustainably, with minimal impacts to landscapes.
Acknowledgments
We thank L. Frid and C. Daniel of ApexRMS for assistance with development of state-and -transition models and simulation in ST-Sim. T. Earnhardt helped develop initial conditions, and R. Gonzalez assisted with biomass to biofuel conversion. We also thank A. Costanza for help with model processing. Funding for this work was provided by the USGS Gap Analysis Program and the Biofuels Center of North Carolina. Any use of trade, product, or firms names is for descriptive purposes only and does not imply endorsement by the U.S. Government.
Conflict of Interest
All authors declare no conflicts of interest in this paper.
Supplementary
1. Biomass to ethanol conversion steps.
2. Full list of deterministic transitions for all state-and -transition models.
3. Full list of probabilistic transitions for all state-and -transition models.
4. List of all initial conditions used as one input into ST-Sim.










 DownLoad:
DownLoad: