1. Introduction
A growing strategy for reducing stock risk is investment in the Chicago Board Options Exchange Volatility Index (VIX), also known as the "fear gauge." The VIX is a benchmark that tracks the volatility of options on the S & P 500 stock index. When investors are concerned about future market declines, they purchase more stock options which drives up the value of the VIX. When market fear is reduced, the VIX declines. The VIX ranges from below 10 in calm times to over 50 during the peak of the 2008 financial crisis.
The VIX itself is not an investable asset. Futures on the VIX began trading in March 2004, while VIX options first trade in February 2006. Depending on an investor's level of sophistication, the VIX can be incorporated into a portfolio in several ways. Retail and professional money managers can directly purchase options and futures on the VIX, or invest indirectly and more easily through exchange-traded products (ETPs) that are available since 2009.
A number of studies document the potential diversification benefits of adding the VIX to a portfolio of stocks. Given the recent creation of tradable VIX indexes and instruments, most studies focus on the portfolio benefits of the VIX during the 2008 global financial crisis (GFC). In this study, we add to the prior literature in three ways. First, in addition to the 2008 GFC, we include the 2011 downgrade of the U.S. government triple-A credit rating, and the 2016 U.K. vote to leave the E.U. (Brexit). Second, we test the VIX against a measure of extreme negative volatility in the equity markets (not necessarily a crisis period). Third, our methodology explores the time varying nature of the VIX utilizing GARCH dynamic conditional correlation analysis as suggested in the prior literature. This methodology is particularly useful in the analysis of time series (such as the VIX) that exhibit non-normal distributions.
This paper investigates the VIX as a hedge and safe haven asset against stock risk for a U.S. based investor. An effective hedge is defined as an asset that is consistently uncorrelated or negatively correlated to stock price movements. A safe haven is an asset that is uncorrelated or negatively correlated to stock price movements during times of market turmoil (Baur and Lucey, 2010). We find that the VIX provides a statistically strong hedge, and either a strong or weak safe haven against stock risk. The VIX is a consistently strong safe haven during all crisis periods tested. The mid-term VIX is superior to the short-term VIX as both a safe haven and its impact on historical portfolio performance.
2. Literature Review
The interest in identifying alternative investment assets is growing for two related reasons. First, rising correlations among country stock markets over time diminish the advantages of international portfolio diversification (Eun and Lee, 2010). Second, the contagion literature demonstrates excessive interdependence in stock markets during the 1987 U.S. stock market crisis, the 1994 Mexican Peso crisis, and the 1997 Asian Crisis (Forbes and Rigobon, 2002). In addition, global crashes are preceded by local and regional crashes as a domino effect (Markwat et al., 2009).
Brenner and Galai (1989) are the first to create a volatility measure, the "sigma index", based on underlying futures and options contracts in 1986. The study suggests that investors can hedge their stock positions by using such an index to reduce the risk of market volatility. The daily VIX index is created by Whaley (1993) and introduced in January 1993, followed by various reformulations thereafter (Whaley, 2009). The VIX index created by Whaley (1993) in 1993 is back-dated to 1986 by historical reconstruction.
There is some disagreement in the literature regarding the benefit of investing in the VIX that warrants further investigation. Daigler and Rossi (2006) conclude that adding a volatility asset to the S & P 500 stock portfolio outweighs the disadvantages. The study illustrates an improvement to the risk-return profile using simulated VIX data from 1992–2002 as exchange traded products are not yet available in the marketplace. Moran and Dash (2007) demonstrate the negative correlation between the VIX and stock returns. They find that a small allocation to VIX futures has potential to reduce stock risk and improve portfolio efficiency. The authors suggest that a longer dataset is needed to fully investigate this benefit. Importantly, they also note that a volatility series is not return generating, and has an expected long-term return of zero. The addition of transaction costs can further erode the benefit of investing in volatility series.
Szado (2009) indicates that the VIX correlation with stocks is both conditional and time-varying. Due to its dynamic nature, the VIX functions more as a diversifier than as a long hedge. However, the VIX is an effective hedge during the 2008 global financial crisis. As the VIX mean reverts and clusters, investment returns in a volatility index are minimized over longer periods.
Chen et al. (2011) shows that short-term VIX futures provide a benefit by expanding the efficient frontier. Warren (2012) observes that the VIX outperforms during periods of weakness in the equity markets, but generally underperforms over time. The study utilizes VIX futures, variance swaps, and forward variance swaps. Conversely, Deng et al. (2012) state that exchange traded products (ETPs) tied to VIX futures do not reduce the variance of equity portfolios, and that using ETPs significantly reduce the returns of equity and bond portfolios. Likewise, Goltz and Stoyanov (2013) also conclude that the VIX is not an effective hedge for passive investors.
Hill (2013) shows that both short-term and mid-term VIX futures products are candidates for tail risk hedging in portfolios, but short-term VIX futures are the most attractive for risk management. In contrast, Whaley (2013) notes the expansion of trading opportunities provided by exchange traded volatility products. The author recommends a limited number of ETPs, specifically those that provide interest accruals. As buy-and-hold investments, Whaley (2013) finds that short-term ETPs are very likely to lose money compared with mid-term ETPs. Alexander and Korovilas (2012) show that numerous ETNs do not behave like the underlying VIX futures. Some ETNs perform well only during the beginning stages of market turmoil, while others perform well during calm times. The authors suggest the creation of new ETNs that will provide attractive long-term investments and effective diversifiers.
As the timing of market volatility is generally unknown, an ongoing investment in a VIX position must potentially be maintained in order to provide an effective hedge. There are historically long periods of time when a VIX investment declines or did not change in value, which clearly diminishes the benefit of this investment as indicated by Whaley (2013). However, Campasano and Linn (2017) and others demonstrate successful trading strategies (e.g., straddles) of volatility products. Johnson (2017) finds that the second principle component of the VIX term structure (Slope) specifically shows the how traders in both VIX ETFs and S & P 500 options can achieve economic benefits.
Bahaji and Aberkane (2016) show that VIX futures improve passive portfolios, but may yield lower utility. Jung (2016) demonstrates with simulated data that VIX futures provide hedging characteristics with caveats. Alexander et al. (2016) conclude that ETPs are effective hedges during the 2008 global financial crisis, but underperform equity portfolios without ETP investment in the long-term. Bordonado et al. (2017) examine price discovery properties, trading profitability, and the hedging ability of ETPs. The authors find that a buy and hold investment in the VIX index does not benefit investors in the S & P 500. Further, ETPs are ineffective hedges, but are potentially profitable under conditions of contango; Sharpe ratios in these circumstances are significantly enhanced. Eraker and Wu (2017) confirm prior findings by Whaley (2013) that the average returns of long-term investment in both VIX futures and VIX ETNs offer negative returns. The authors develop an equilibrium model to explain the negative returns.
Our study differs from the prior literature in several ways. First, due to the recent development of investable VIX indexes (since 2006), a long-term dataset is critically important to produce results that are generalized; our time horizon expands into 2016, which provides over 10 years of useful data. The expanded data includes three significant events that test the VIX: the 2008 GFC, the 2011 downgrade of the U.S. government triple-A credit rating, and the 2016 U.K. vote to leave the E.U. (Brexit). Second, we test the VIX against a measure of extreme negative volatility in the equity markets (not necessarily a crisis period). To our knowledge, no other studies investigate volatility in this manner. Third, our methodology explores the dynamic and time varying nature of the VIX by utilizing GARCH dynamic conditional correlation. Szado (2009) and others recognize the importance of the time varying nature of the VIX, and we are the first to apply this methodology that is specifically suited to such an analysis.
3. Data and Methodology
3.1. Data description
A variety of exchange traded products including ETNs and ETFs are available for investment since 2009, and are generally growing in popularity since their creation. Investments in ETPs are subject to a number of risks and limitations. However, as a potential safe haven asset, the liquidity of instruments based on the VIX actually improves during market turmoil unlike some other traditional hedges (Bahaji and Aberkane, 2016).
For illustrative purposes, Table 1 reports descriptive statistics for the two largest ETNs and ETFs that compare with the short-term and mid-term VIX indexes used in this study as follows: (VXX) iPath S & P 500 VIX ST Futures ETN, (VXZ) iPath S & P 500 VIX Mid-Term Futures ETN, (VIXY) ProShares VIX Short-Term Futures ETF, (VIXM) ProShares VIX Mid-Term Futures ETF. The start date of 2009 and beyond is relatively short compared with the actual VIX short-term and mid-term futures indexes that begin trading in 2006. Net assets in the short-term ETPs are significantly larger than the mid-term ETPs. The short-term ETPs have more negative mean daily returns than their mid-term equivalents. The short-term ETPs have at least double the volatility of the mid-term ETPs as observed in the standard deviation.
Table 1. Descriptive statistics for Exchange Traded Notes & Funds (ends July 2016).
| Symbol |
Type |
Maturity |
Mean (%) |
Standard Dev. (%) |
Inception date |
Net assets (USD 2017) |
| VXX |
ETN |
ST |
-0.2570 |
3.8895 |
Jan 29,2009 |
962 M |
| VXZ |
ETN |
MT |
-0.1015 |
1.9428 |
Jan 29,2009 |
30 M |
| VIXY |
ETF |
ST |
-0.1987 |
4.0640 |
Jan 3,2011 |
149 M |
| VIXM |
ETF |
MT |
-0.1109 |
1.9883 |
Jan 3,2011 |
31 M |
Unlike investing directly in VIX futures indexes, ETPs are subject to unique weaknesses. While an ETF represents a basket of actual securities, an ETN is a bond issued by a financial institution. The institution promises to repay the bond based on an underlying index. As such, the credit quality of the issuing institution is an additional risk factor. While ETNs carry credit risk, institutions do promise to pay the exact value of the index that they represent. ETFs contain possible "tracking errors" of the index that they're trying to mimic, as they own individual securities (contracts) that may not represent the exact value of the index at all times.
Rollover is process of closing out a futures contract that is close to expiration and then purchasing a new contract with a later maturity date. The new contract may come at a higher or lower cost, but adds to the risk of managing the position. The pricing of futures contracts can be further complicated. Contango exists if the futures price is above the expected future spot rate. As convergence must occur, this implies that the futures price is expected to decline over time and is unfavorable to the investor. In contrast, normal backwardation is when the futures price is below the expected future spot, which indicates that it will rise over time (favorable to the investor).
There are two main proxies for most ETPs that are available to risk managers, investors, and volatility traders: the S & P500 VIX Short-Term Futures Index (STVIX) and the S & P500 VIX Mid-Term Futures Index (MTVIX). The STVIX maintains a constant one-month rolling position in first and second month VIX futures contracts. The MTVIX measures the volatility of the fourth, fifth, sixth, and seventh month VIX futures, and seeks to maintain a five-month constant maturity. Both indexes are rebalanced on a daily basis and are comprised of VIX spot movements, futures roll-yield costs, and collateral interest. While officially launched in January 2009, back-tested index data is available from December 2005.
Daily data for the total return series of the STVIX and MTVIX are collected from the DataStream database for the period January 2006 through July 2016. The total return of the S & P 500 composite index (SP500) represents investment in U.S. stocks. To achieve stationarity, all series are transformed into first-difference form. Table 2 contains descriptive statistics for the three series.
Table 2. Descriptive statistics for the daily returns in percentages, January 2006 – July 2016. Sharpe ratio is calculated at 10% for each VIX index.
| Index |
Observ. |
Mean |
Standard Deviation |
Minimum |
Maximum |
Sharpe Ratio |
| STVIX |
2662 |
-0.1365 |
4.1444 |
-18.8480 |
32.7081 |
5.9106 |
| MTVIX |
2662 |
-0.0326 |
2.0610 |
-9.1488 |
13.4130 |
8.9912 |
| SP500 |
2662 |
0.0376 |
1.2909 |
-9.0259 |
11.5811 |
9.9110 |
The daily mean return is negative for the STVIX (-0.1365%) with a standard deviation of 4.1444%. The mean return for the MTVIX (-0.0326%) is significantly less negative with a lower standard deviation (2.0610%). By contrast, the S & P500 mean (0.0376) is positive with a relatively lower standard deviation (1.2909%) than both VIX indexes. While the MTVIX has a negative mean return, the minimum (-9.1488%) and maximum (13.4130%) return values are comparable to those of the S & P500 (-9.0259% to 11.5811%). The STVIX has a wider variation in returns over time from -18.8480% to 32.7081% compared with the MTVIX. The Sharpe ratio for the unhedged SP500 is 9.9110%. Assuming an arbitrary 10% investment in the MTVIX, the Sharpe ratio is statistically similar to the SP500 at 8.9912%. However, the STVIX noticeably underperforms at 5.9106%. These findings are consistent with Whaley (2013) regarding the potential losses associated with short-term VIX investments, and with Bordonado et al. (2017) on the Sharpe ratio results.
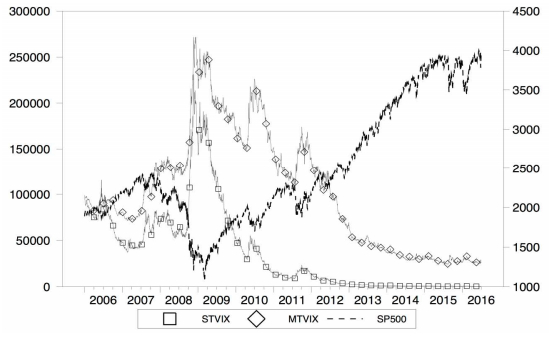
Figure 1 shows a time series graph of the STVIX, MTVIX, and the S & P500 in non-differenced form from January 2006 through July 2016. The levels demonstrate the negative relationship between the VIX indexes and stock prices, especially during the 2008 financial crisis period. This is consistent with prior studies, and suggests that the VIX is a potential hedge against stock risk. The MTVIX appears to be more responsive to changes in the S & P500 compared with the STVIX, which is potentially advantageous for hedging purposes.
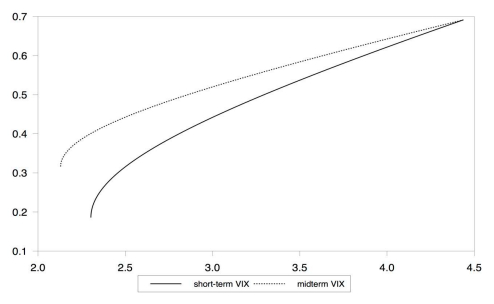
To show the potential risk reduction benefits of investing in volatility indexes, efficient portfolios are formed from January 2006 through July 2016. Using monthly total return data, Figure 2 contains efficient frontiers of the STVIX added to S & P500, and the MTVIX added to the S & P500. The portfolios are mean-variance efficient for a given level of expected return, and the model does not allow for short sales or risk-free investments. The portfolio weights are constrained to have nonnegative values. The upper right-hand corner of the graph at the convergence of the two lines represents a 100% investment in the S & P500. Adding investment in either VIX index appears to reduce portfolio risk with a relatively smaller reduction in portfolio return. The MTVIX clearly provides superior performance with a larger return-to-risk profile compared with the STVIX. Diminishing benefits will ultimately occur as investment in the VIX indexes are maximized as shown. As this procedure is performed on an ex post basis for illustrative purposes, we are not providing specific recommendations for asset allocations.
3.2. Methodology
Dynamic conditional correlation (DCC) is a technique developed by Engle (2002) to examine time-varying correlation. The procedure uses GARCH to generate time-varying estimates of the conditional co-movement between assets implemented as:
|
$
{{\text{r}}_{\text{t}}}\left| {{\text{I}}_{\text{t}-1}} \right.\tilde{\ }\text{N}\left( 0,{{\text{H}}_{\text{t}}} \right)
$
|
(1)
|
|
$
{{\text{H}}_{\text{t}}}={{\text{D}}_{\text{t}}}{{\text{R}}_{\text{t}}}{{\text{D}}_{\text{t}}}
$
|
(2)
|
where rt is the k x 1 demeaned vector of variables conditional on information It-1, and is assumed to be conditionally multivariate normal. Ht is the covariance matrix where Rt is the k x k time-varying correlation matrix, and Dt is the k x k diagonal matrix of conditional standardized residuals estimated from the univariate GARCH models.
The general form equation of the likelihood function of the estimator is given by:
|
$
\text{L}=-0.5\underset{\text{t}=1}{\overset{\text{T}}{\mathop \sum }}\,(\text{klog}\left( 2\text{ }\!\!\pi\!\!\text{ } \right)+2\text{log}\left( \left| {{\text{D}}_{\text{t}}} \right| \right)+\text{log}\left( \left| {{\text{R}}_{\text{t}}} \right| \right)+{{\overset{\acute{\ }}{\mathop{\text{ }\!\!\varepsilon\!\!\text{ }}}\,}_{\text{t}}}\text{R}_{\text{t}}^{-1}{{\text{ }\!\!\varepsilon\!\!\text{ }}_{\text{t}}})
$
|
(3)
|
There are two steps in this procedure. The volatility component Dt is maximized in the first step by replacing Rt with a k x k identity matrix. This results in reducing the log likelihood to the sums of the log likelihoods of the univariate GARCH equations. The first order univariate GARCH models are estimated for each VIX index and the S & P500 using the Glosten et al. (1993) model allowing for asymmetries:
|
$
{{\text{h}}_{\text{t}}}={{\text{c}}_{0}}+{{\text{a}}_{1}}\text{ }\!\!\varepsilon\!\!\text{ }_{\text{t}-1}^{2}+{{\text{b}}_{1}}{{\text{h}}_{\text{t}-1}}+{{\text{d}}_{1}}\text{ }\!\!\varepsilon\!\!\text{ }_{\text{t}-1}^{2}{{\text{I}}_{\text{t}-1}}
$
|
(4)
|
where ht is the conditional variance, d1 is the asymmetry term, and It-1=1 if εt < 0, otherwise I=0. The correlation component Rt is maximized in the second step:
|
$
{{\text{R}}_{\text{t}}}=\left( 1-\text{ }\!\!\alpha\!\!\text{ }-\text{ }\!\!\beta\!\!\text{ } \right)\overline{\text{R}}+\text{ }\!\!\alpha\!\!\text{ }{{\text{ }\!\!\varepsilon\!\!\text{ }}_{\text{t}-1}}{{\overset{\acute{\ }}{\mathop{\text{ }\!\!\varepsilon\!\!\text{ }}}\,}_{\text{t}-1}}+\text{ }\!\!\beta\!\!\text{ }{{\text{R}}_{\text{t}-1}}
$
|
(5)
|
where the values of the DCC parameters α and β are determined. If α and β are zero, then Rt reduces to R, which would indicate that the constant correlation model is appropriate.
Subsequent to the GARCH estimation, the time varying correlations Rt are extracted from model (5) into a separate time series for each VIX index. Rt are regressed on dummy variables representing market turmoil to test each VIX index as a hedge and safe haven asset against stock risk. The following hypotheses are formulated:
H1: The VIX does not provide a hedge against stock risk in the S & P500.
H2: The VIX is not a safe haven against extreme negative moves in the S & P500.
The hypotheses are assessed with models (6) and (7):
|
$
{{\text{R}}_{\text{t}}}={{\text{ }\!\!\gamma\!\!\text{ }}_{0}}+{{\text{ }\!\!\gamma\!\!\text{ }}_{1}}\text{D}\left( {{\text{r}}_{\text{stock}}}{{\text{q}}_{10}} \right)+{{\text{ }\!\!\gamma\!\!\text{ }}_{2}}\text{D}\left( {{\text{r}}_{\text{stock}}}{{\text{q}}_{5}} \right)+{{\text{ }\!\!\gamma\!\!\text{ }}_{3}}\text{D}\left( {{\text{r}}_{\text{stock}}}{{\text{q}}_{1}} \right)
$
|
(6)
|
where D represent dummy variables that capture extreme movements in the S & P500 at the 10%, 5%, and 1% quantiles. The VIX is a weak hedge if γ0 are insignificantly different than zero, a strong hedge if γ0 is significantly negative, or a diversifier if γ0 is significantly positive. The VIX is a weak safe haven if the γ1, γ2, or γ3 coefficients are insignificantly different from zero, or a strong safe haven if γ1, γ2, or γ3 are significantly negative. Significantly positive γ1, γ2, or γ3 coefficients indicate that the VIX is not a safe haven during the extreme stock volatility.
To examine the VIX as a hedge or safe haven against stock risk during a period of global economic or political crisis, a modified version of a dummy variable regression is empirically tested as:
|
$
{{\text{R}}_{\text{t}}}\text{=}{{\text{ }\!\!\gamma\!\!\text{ }}_{\text{0}}}\text{+}{{\text{ }\!\!\gamma\!\!\text{ }}_{\text{1}}}\text{D}\left( \text{GFC} \right)\text{+}{{\text{ }\!\!\gamma\!\!\text{ }}_{\text{2}}}\text{D}\left( \text{UScredit} \right)\text{+}{{\text{ }\!\!\gamma\!\!\text{ }}_{\text{3}}}\text{D}\left( \text{Brexit} \right)
$
|
(7)
|
where a dummy variable is set to one at the start of three periods of crisis: the global financial crisis (9/10/08), the downgrade of the U.S. government triple-A credit rating by Standard & Poor's (8/5/11), and the U.K. vote to exit the European Union (6/23/16). The VIX is a weak hedge if γ0 is insignificantly different than zero, a strong hedge if γ0 is significantly negative, or a diversifier if γ0 is significantly positive. The VIX is a weak safe haven in specific crisis periods if the γ1,
γ2, γ3 coefficients are insignificantly different than zero or a strong safe haven if they are significantly negative. Significantly positive γ1, γ2, γ3 coefficients indicate that the VIX is not a safe haven during the crisis period.
4. Results and Discussion
Descriptive statistics for the daily dynamic conditional correlations between the STVIX with the S & P500, and the MTVIX with the S & P500, are provided in Table 3.
Table 3. Descriptive statistics for the dynamic conditional correlations, January 2006 – July 2016.
| Index |
Observ. |
Mean |
Standard Deviation |
Minimum |
Maximum |
| STVIX |
2661 |
-0.8352 |
0.0446 |
-0.9582 |
-0.6561 |
| MTVIX |
2661 |
-0.7779 |
0.0608 |
-0.8987 |
-0.5026 |
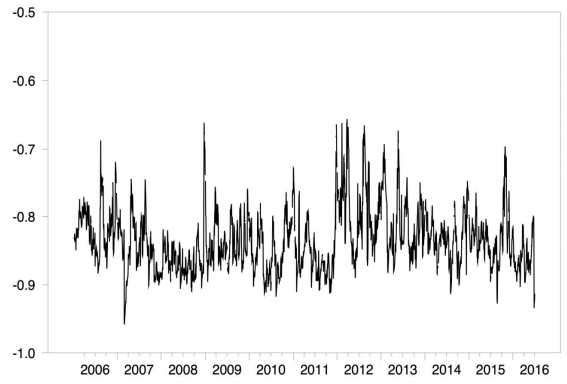
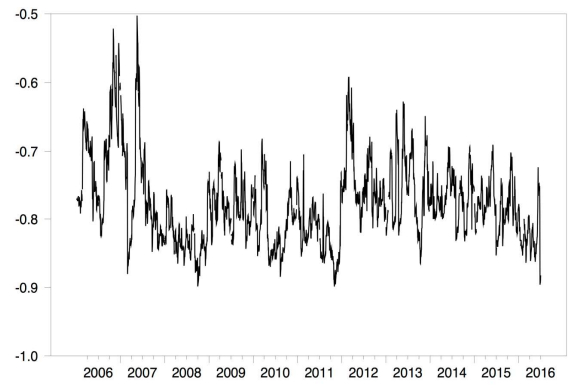
The mean correlation for the STVIX (-0.8352) and the MTVIX (-0.7779) are both highly negative indicating potentially beneficial hedging properties. The standard deviation for the STVIX (0.0446) shows lower volatility than the MTVIX (0.0608). Lower volatility suggests a lower level of responsiveness to changes in stocks. The dynamic correlations are graphically presented in Figure 3 for the STVIX and Figure 4 for the MTVIX. The graphs demonstrate wider variability of the MTVIX compared with the STVIX, and also illustrate the non-constant (i.e., dynamic) nature of the correlations over time.
Two models are estimated to test the VIX as a hedge and safe haven against stock risk. First, the time series of the DCC coefficients Rt between each VIX index and the S & P500 are regressed on dummy variables representing three quantiles of extreme negative stock market volatility. Second, the DCC coefficients Rt are regressed on dummy variables representing the 2008 global financial crisis, the 2011 downgrade of the U.S. government triple-A credit rating by Standard & Poor's, and the 2016 U.K. vote to leave the E.U. (Brexit).
Table 4 shows the estimates of regressions based on model (6). The DCC coefficients are regressed on a constant and three dummy variables representing levels of extreme negative stock volatility quantiles of 10%, 5%, and 1%. The "hedge" column represents the model constant γ0, which shows a negative relationship between stocks and the STVIX (-0.8334), and the MTVIX (-0.7749), with significance at the 1% level. A significant negative value indicates that both VIX indexes are strong hedges against stock risk, and leads to a rejection of the first hypothesis (H1).
Table 4. The VIX as a hedge and safe haven against stock risk during extreme stock volatility.
|
|
Stock Quantile |
| Index |
Hedge (γ0) |
10% (γ1) |
5% (γ2) |
1% (γ3) |
| STVIX |
-0.8334*** |
-0.0187*** |
0.0024 |
-0.0160* |
| MTVIX |
-0.7749*** |
-0.0207*** |
-0.0033 |
-0.0314*** |
Note: ***, **, * indicates significance at the 1%, 5%, and 10% levels, respectively.
Model: ${{R}_{t}}={{\gamma }_{0}}+{{\gamma }_{1}}D\left({{r}_{stock}}{{q}_{10}} \right)+{{\gamma }_{2}}D\left({{r}_{stock}}{{q}_{5}} \right)+{{\gamma }_{3}}D\left({{r}_{stock}}{{q}_{1}} \right)$ |
The stock quantile regression coefficients (γ1, γ2, γ3) represent the safe haven characteristics of the VIX and stocks. Significant negative coefficients indicate a strong safe haven in the 10% stock quantile in both STVIX (-0.0187) and the MTVIX (-0.0207). In the more extreme 5% quantile, neither VIX index is significantly different than zero. Insignificant coefficients indicate that both VIX indexes are a weak safe haven in this quantile. In the most extreme 1% stock quantile, both VIX indexes are strong safe havens, but the MTVIX (-0.0314) shows greater statistical significance than the STVIX (-0.0160). As both VIX indexes are either a strong or weak safe haven, the second hypothesis (H2) is rejected.
The final model tests the VIX as a hedge and safe haven during periods of financial and political crisis based on model (7), and the results are presented in Table 5. The model constant γ0 for the "hedge" column is statistically consistent with model (6). During the 2008 global financial crisis, significant negative coefficients indicate that the STVIX (-0.0495) and the MTVIX (-0.0982) are strong safe havens from stock risk. Likewise, during the 2011 downgrade of the U.S. government credit rating, significant negative γ2 coefficients are observed in both the STVIX (-0.0506) and the MTVIX (-0.0679). Lastly, during the Brexit vote period the STVIX (-0.0754) and the MTVIX (-0.0968) indexes are strong safe havens. In all cases, the coefficients of the MTVIX are more negative than the STVIX, which demonstrates potentially greater safe haven properties.
Table 5. The VIX as a hedge and safe haven against stock risk during financial and political crises.
|
|
Crisis Period |
| Index |
Hedge (γ0) |
GFC (γ1) |
UScredit (γ2) |
Brexit (γ3) |
| STVIX |
-0.8344*** |
-0.0495*** |
-0.0506*** |
-0.0754*** |
| MTVIX |
-0.7760*** |
-0.0982*** |
-0.0679*** |
-0.0968*** |
Note: ***, **, * indicates significance at the 1%, 5%, and 10% levels, respectively.
Model: ${{\text{R}}_{\text{t}}}\text{=}{{\text{ }\!\!\gamma\!\!\text{ }}_{\text{0}}}\text{+}{{\text{ }\!\!\gamma\!\!\text{ }}_{\text{1}}}\text{D}\left(GFC \right)\text{+}{{\text{ }\!\!\gamma\!\!\text{ }}_{\text{2}}}\text{D}\left(\text{UScredit} \right)\text{+}{{\text{ }\!\!\gamma\!\!\text{ }}_{\text{3}}}\text{D}\left(\text{Brexit} \right)$ |
5. Conclusion
This study investigates the hedging properties of the VIX index, a growing popular strategy for reducing stock risk. We add to the literature by evaluating the hedging and safe haven characteristics of investing in the short-term VIX futures index and the mid-term VIX futures index during times of extreme negative volatility in the stock market, and during times of financial and political crisis. Our investigation goes beyond the 2008 global financial crisis that is the subject of some recent studies, and we utilize GARCH dynamic conditional correlation (DCC) to examine the time varying relationship between the VIX futures indexes and stocks.
The major findings are as follows: first, negative mean DCC coefficients indicate that the VIX futures indexes are inversely related to stocks, supporting the diversification potential of investing in volatility indexes. Second, results of DCC coefficients regressed on dummy variables representing stock market volatility, and periods of financial and political crises, show that the VIX futures indexes are a strong hedge against stock risk. Third, during periods of extreme negative stock market volatility, the VIX futures indexes are a strong or weak safe haven against stock risk. Fourth, the VIX futures indexes are a strong safe haven against stock indexes during the 2008 global financial crisis, the 2011 downgrade of the U.S. government credit rating, and the 2016 U.K. Brexit vote.
The results support the potential role of adding VIX futures index investment to a portfolio of U.S. stocks. VIX futures investment provides a significant hedge and safe haven during times of turmoil in the stock market. As shown both in this study and some prior literature, a simple buy and hold investment is likely to produce negative returns over longer periods of time. In our sample, the short-term VIX futures index adversely affects the performance of historic portfolios, while the mid-term VIX futures index has a neutral impact. Prior studies using earlier data demonstrate beneficial portfolio effects. As such, without accurately timing market turmoil or excessive volatility, investors are advised to utilize more sophisticated trading strategies than passive buy and hold.
Conflict of Interest
All authors declare no conflict of interest.









 DownLoad:
DownLoad: