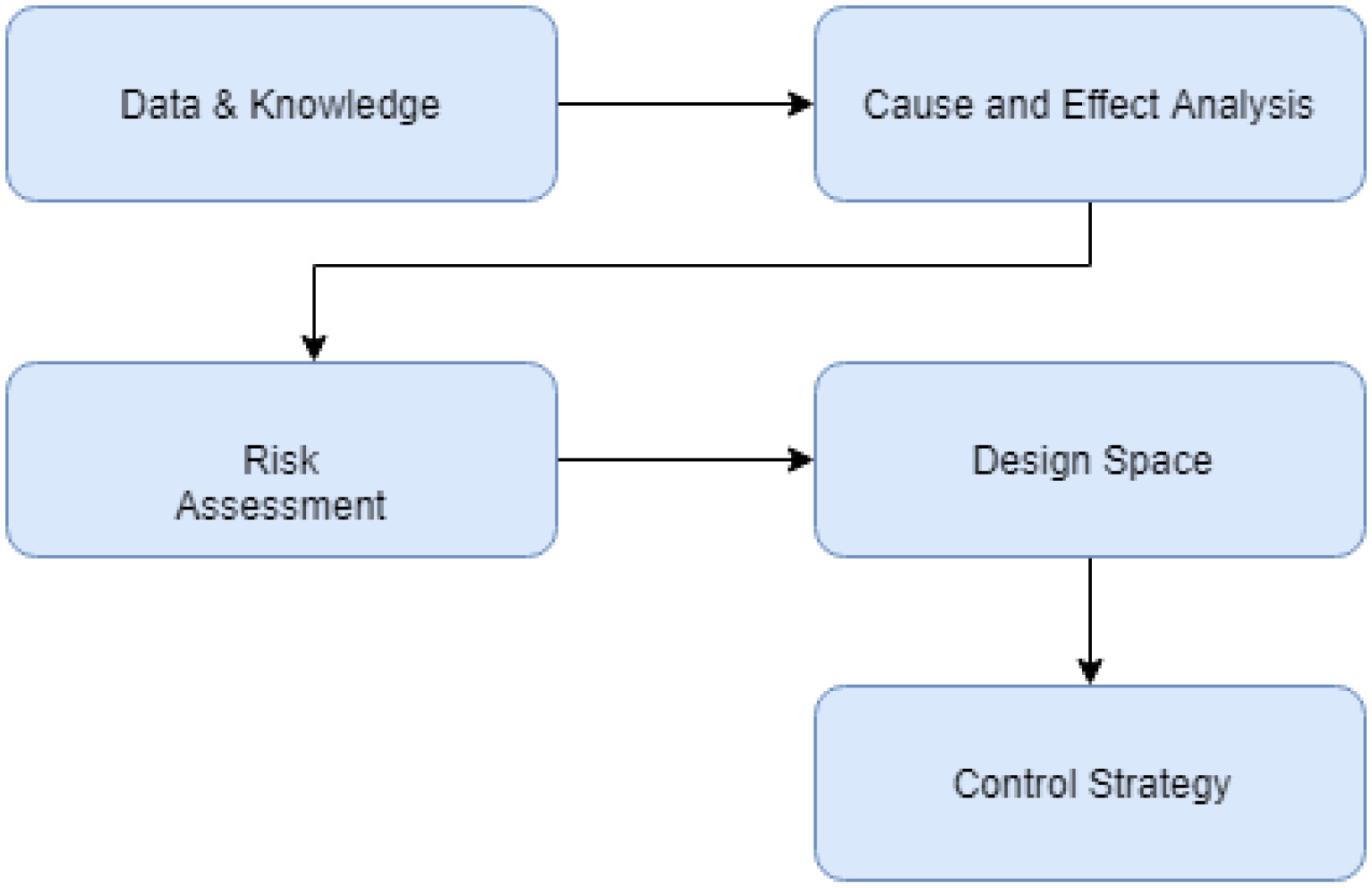
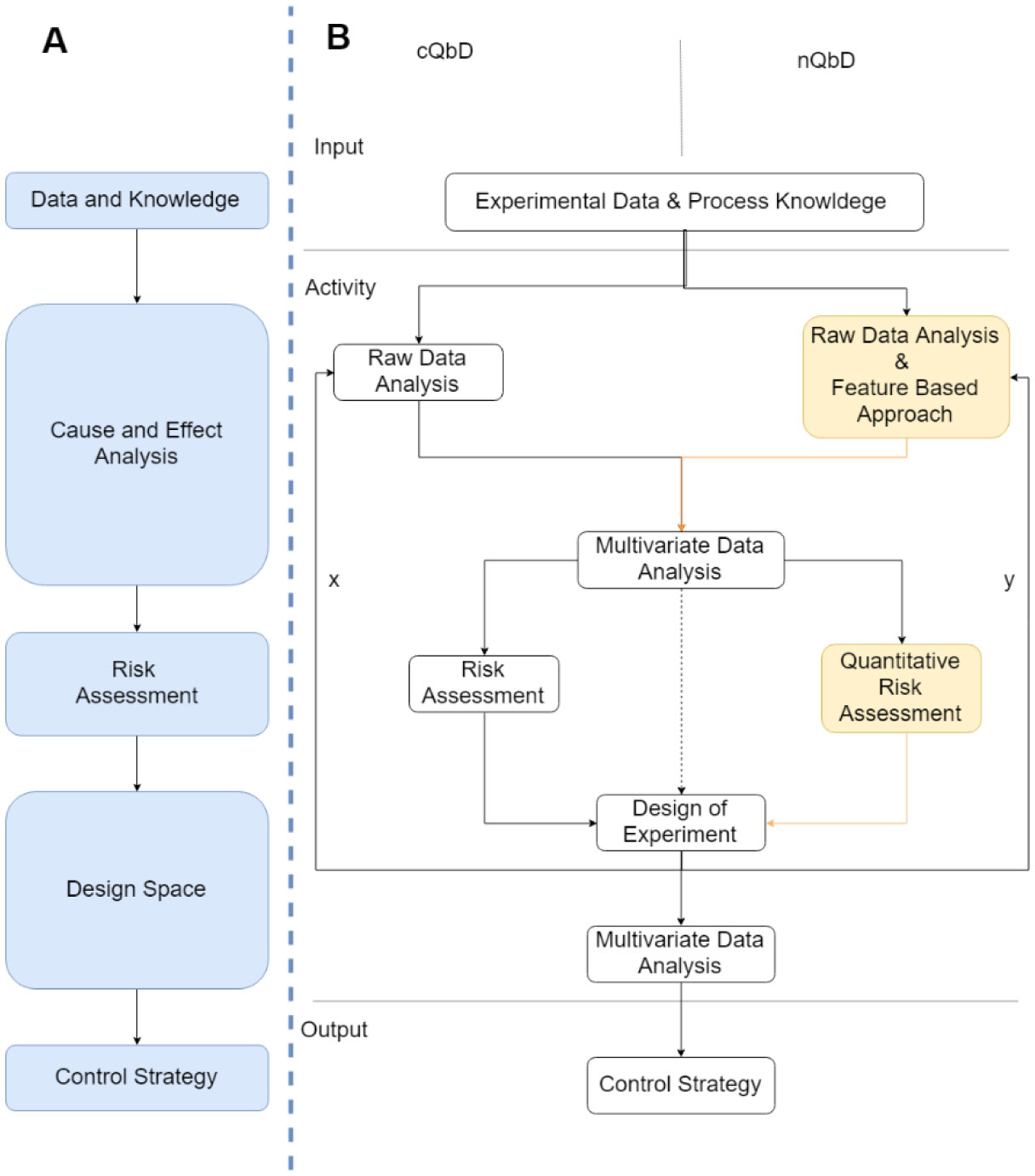
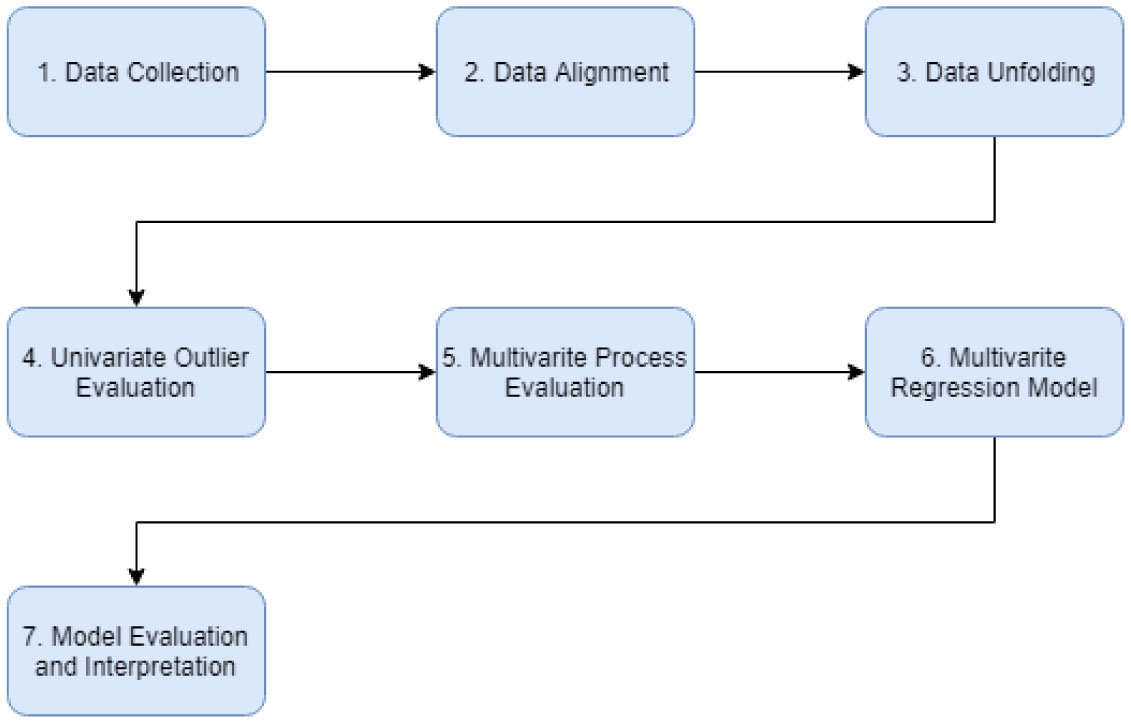
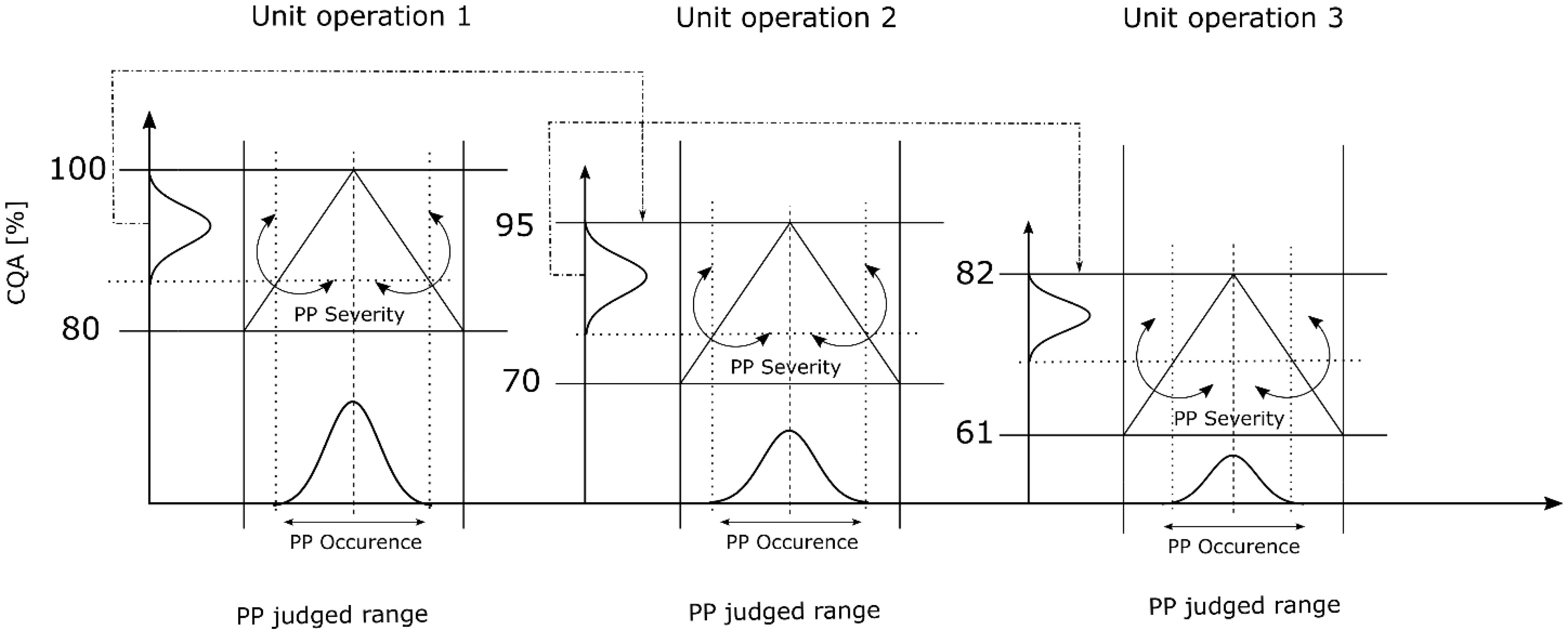
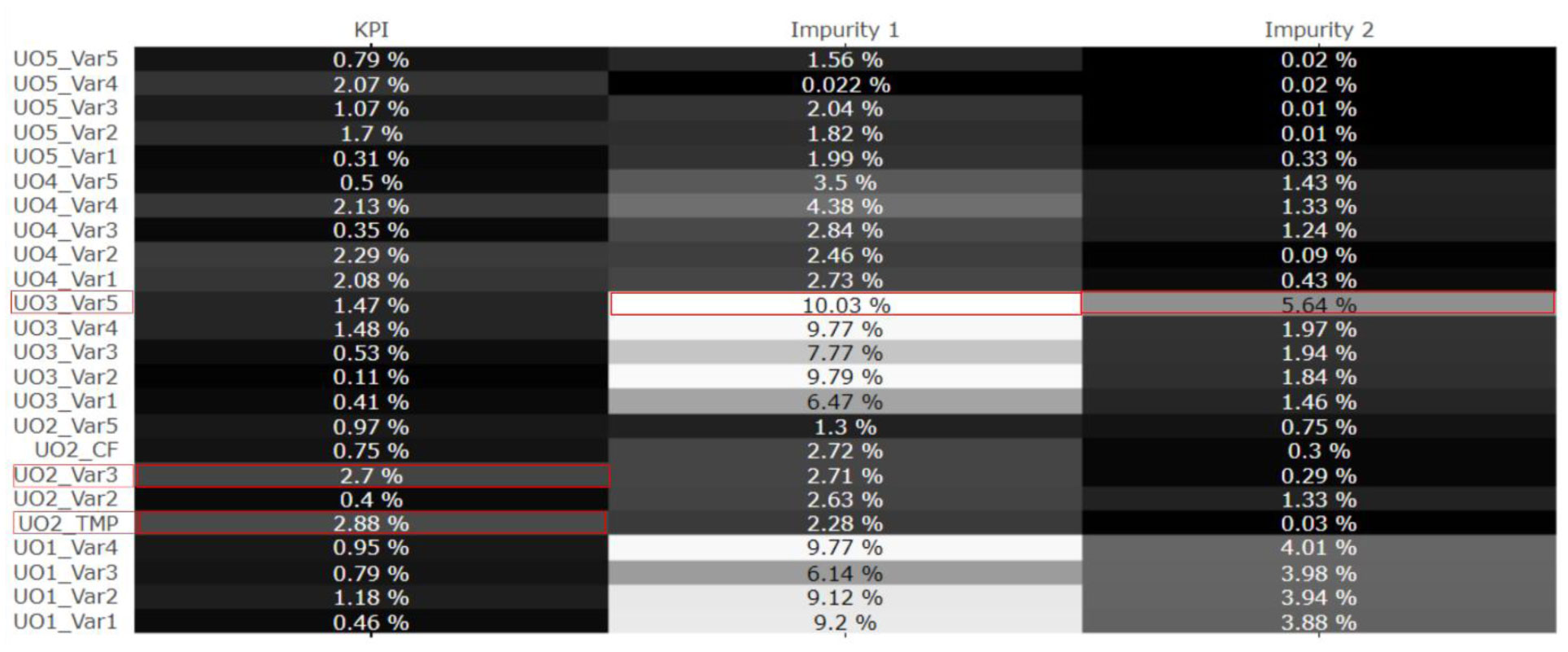
A Process characterization is a regulatory imperative for process validation within the biopharmaceutical industry. Several individual steps must be conducted to achieve the final control strategy. For that purpose, tools from the Quality by Design (QbD) toolbox are often considered. These tools require process knowledge to conduct the associated data analysis. They include cause and effect analysis, multivariate data analysis, risk assessment and design space evaluation. However, this approach is limited to the evaluation of single unit operations. This is risky as the interactions of the operations may render the control strategy invalid. Hence, a holistic process evaluation is required. Here, we present a novel workflow that shows how simple data analysis tools can be used to investigate the process holistically. This results in a significant reduction of the experimental effort and in the development of an integrated process control strategy. This novel QbD workflow is based on a novel combination of risk assessment and integrated process modeling. We demonstrate this workflow in a case study and show that the herein presented approach can be applied to any biopharmaceutical process. We demonstrate a workflow that can reduce the number of factors and increase the amount of responses within a Design of Experiments (DoE). Consequently, this result demonstrates that experimental costs and time can be reduced by investing more time in thoughtful data analysis.
1.
Introduction
Fractional differential equations frequently appear in the mathematical modelling of many physical and engineering problems. One can find the potential application of fractional-order operators in malaria and HIV/AIDS model [1], bioengineering [2], ecology [3], viscoelasticity [4], fractional dynamical systems [5,6] and so forth. Influenced by the practical applications of fractional calculus tools, many researchers turned to the further development of this branch of mathematical analysis. For the theoretical background of fractional derivatives and integrals, we refer the reader to the texts [7], while a detailed account of fractional differential equations can be found in [8,9,10]. In a recent monograph [11], the authors presented several results on initial and boundary value problems of Hadamard-type fractional differential equations and inclusions.
Fractional-order differential equations equipped with a variety of boundary conditions have been studied in the last few decades. The literature on the topic includes the existence and uniqueness results related to classical, periodic/anti-periodic, nonlocal, multi-point, and integral boundary conditions; for instance, see [12,13,14,15,16,17,18,19,20,21] and the references therein.
Recently, in [22], Ahmad et al. considered a boundary value problem involving sequential fractional derivatives given by
supplemented with nonlocal integro-multipoint boundary conditions:
where cDq,cDκ denote the Caputo fractional derivative of order q and κ respectively (for the definition of Caputo fractional derivative, see Definition 2.2), f is a given continuous function, ρp(p=1,2,3,4) are real constants and αi,δi(i=1,2,…,m−2),rj,γj(j=1,2,…,p−2), are positive real constants. Existence and uniqueness results for the problem (1.2) were proved by using the fixed point theorems due to Banach and Krasnoselskii.
In [23], Ahmad et al. studied the existence and uniqueness of solutions for a new class of boundary value problems for multi-term fractional differential equations supplemented with four-point boundary conditions
where CDχ is Caputo fractional derivatives of order χ∈{α,β,γ}, λ,ν,μ∈R, 1<α≤2, 1<β<α, 0≤γ<α−β<1, δ>0, Iδ is the Riemann-Liouville fractional integral of order δ, and f:[0,T]×R→R is a continuous function.
In [24], the authors studied the existence of solutions for a nonlinear Liouville-Caputo-type fractional differential equation on an arbitrary domain:
supplemented with non-conjugate Riemann-Stieltjes integro-multipoint boundary conditions of the form:
where cDqa denotes the Caputo fractional derivative of order q, a<η1<η2<⋯<ηn−2<b, f:[a,b]×R⟶R is a given continuous function, A is a function of bounded variation, and αi∈R, i=1,2,⋯,n−2.
In the present paper, we investigate the existence of solutions for an abstract nonlinear multi-term Caputo fractional differential equation with nonlinearity depending on the unknown function together with its lower-order Caputo fractional derivatives given by
supplemented with Riemann-Stieltjes integro-multipoint boundary conditions
where cDθa denotes the Caputo fractional differential operator of order θ with θ=q,r,p, a<η1<η2<⋯<ηn−2<b, f:[a,b]×R3⟶R is a given continuous function, A is a function of bounded variation, and μ(μ≠0),ξ,αi∈R, i=1,2,⋯,n−2.
The rest of the paper is arranged as follows. In section 2, we prove a basic result related to the linear variant of the problem (1.6)-(1.7), which plays a key role in the forthcoming analysis. We also recall some basic concepts of fractional calculus. The existence result is presented in Section 3, while the uniqueness result in Section 4. Examples illustrating the obtained results are also presented. The paper concludes with Section 5 with some interesting observations.
2.
Basic result
Before presenting an auxiliary lemma, we recall some basic definitions of fractional calculus [8].
Definition 2.1. The Riemann-Liouville fractional integral of order σ with lower limit a for function ϕ is defined as
provided the integral exists.
Definition 2.2. For (n-1)-times absolutely continuous function ϕ:(a,∞)⟶R, the Caputo derivative of fractional order σ is defined as
where [σ] denotes the integer part of the real number σ.
In passing we remark that we write cDσa and Iσa as cDσ and Iσ respectively when a=0.
Lemma 2.1. [8] For n−1<q<n, the general solution of the fractional differential equation cDqax(t)=0,t∈(a,b), is
where ci∈R,i=0,1,…,n−1. Furthermore,
Lemma 2.2. Let ψ∈C([a,b]). Then the unique solution of the linear multi-term fractional differential equation
subject to the boundary conditions (1.7) is given by
where
and it is assumed that γ1≠0.
Proof. Applying the integral operator Iqa on both sides of fractional differential equation (2.1) and using Lemma 2.1, we get
where ci∈R,i=0,1,2,3 are unknown arbitrary constants. Using the boundary conditions (1.7) in (2.10) and (2.11), we obtain c1=0 and
where Ai(i=1,2,3) are given by (2.8), (2.9) and
Eliminating c0 from (2.12) and (2.14), we get
Solving (2.13) and (2.16), we find that
where δi and σi(i=1,2,3) are defined by (2.5) and (2.6) respectively. Using (2.17) and (2.18) in (2.12), we get
where λi(i=1,2,3) are given by (2.4). Inserting the values of c0,c1,c2 and c3 in (2.10) together with notations (2.3), we obtain the solution (2.2). The converse of the lemma follows by direct computation.
Now we recall some preliminary concepts from functional analysis related to our work.
Definition 2.3. Let Ω be a bounded set in metric space (Y,d). The Kuratowski measure of noncompactness, α(Ω), is defined as
Definition 2.4. [25] Let J:D(J)⊆Y⟶Y be a bounded and continuous operator on Banach space Y. Then J is called a condensing map if α(J(A))<α(A) for all bounded sets A⊂D(J), where α denotes the Kuratowski measure of noncompactness.
Lemma 2.3. [26] The map F+G is a k-set contraction with 0≤k<1, and thus also condensing, if the following conditions hold:
(i) F,G:D⊆Y⟶Y are operators on the Banach space Y;
(ii) F is k-contractive, that is, for all x,y∈D and a fixed k∈[0,1), ‖Fx−Fy‖≤k‖x−y‖;
(iii) G is compact.
Lemma 2.4. (Sadovskii Theorem [27]) Let A be a convex, bounded and closed subset of a Banach space Y and J:A⟶A be a condensing map. Then J has a fixed point.
3.
Existence of solutions
For 0<p≤1, let A={x:x,cDpax(t),cDp+1ax(t)∈C([a,b],R)} denote the Banach space of all continuous functions from [a,b]⟶R endowed with the norm defined by
In view of Lemma 2.2, we transform the problem (1.6)-(1.7) into an equivalent fixed point problem as
where F:A⟶A is defined by
where ϕi(t),i=1,2,3 are defined by (2.3) and ˆf(x(t))=f(t,x(t),cDpax(t),cDp+1ax(t)).
From (3.3), we have
where
and
where
For the sake of computational convenience, we introduce
where ˉϕi=supt∈[a,b]|ϕi(t)|,ˉωi=supt∈[a,b]|ωi(t)|,ˉνi=supt∈[a,b]|νi(t)|,i=1,2,3,
In the following result, we prove the existence of solutions for the problem (1.6)-(1.7) by applying Lemma 2.4.
Theorem 3.1. Let f:[a,b]×R3⟶R be a continuous function. Assume that:
(O1) there exists a function ρ∈C([a,b],R+) such that
(O2) κ<1, where κ=3Δ and Δ is defined by (3.11).
Then problem (1.6)-(1.7) has at least one solution on [a,b].
Proof. Consider a closed bounded and convex ball Bτ={x∈A:‖x‖∗≤τ}⊆A, where τ is a fixed constant. Let us define F1,F2:Bτ⟶Bτ by
Observe that,
Now we show that F1 and F2 satisfy all the conditions of Lemma 2.4. The proof will be given in several steps.
Step 1. FBτ⊂Bτ.
Let us choose τ≥3‖ρ‖ˉΔ1−κ, where κ is defined in (O2) and ˉΔ is given by (3.12). For x∈Bτ, we have
Similarly, it can be shown that
Hence
Thus we get FBτ⊂Bτ.
Step 2. F1 is a κ-contractive.
For x,y∈Bτ and using the condition O2, we have
Similarly, we can obtain
Hence
which proves that F1 is κ-contractive.
Step 3. F2 is compact.
Continuity of f implies that the operator F2 is continuous. Also, F2 is uniformly bounded on Bτ as
which imply that ‖F2x‖∗≤3‖ρ‖ˉΔ.
Let t1,t2∈[a,b] with t1<t2 and x∈Bτ. We have
and
The right hand sides of the inequalities (3.13)-(3.15) tend to zero as t2−t1⟶0 independent of x. Thus, F2 is equicontinuous on Bτ. Therefore, by Arzelá-Ascoli theorem, F2 is a relatively compact on Bτ.
Step 4. F is condensing. Since F1 is continuous, κ-contractive and F2 is compact, therefore, by Lemma 2.3, the operator F:Bτ⟶Bτ, with F=F1+F2 is a condensing map on Bτ.
Hence, by Lemma 2.4, the operator F has a fixed point. Therefore, the problem (1.6)-(1.7) has at least one solution on [a,b].
Example 3.1. Consider the fractional boundary value problem.
where q=359,r=18,p=14, a=0,b=1, μ=45, ξ=9,α1=−1300, α2=−122, α3=1240, α4=239, η1=117, η2=217, η3=317, η4=417, and
Let us take A(s)=s22. Using the given data, we have that A1≃−0.493339, A2≃0.252328, A3≃0.200616, γ1≃−0.849088, γ2≃−0.372834, σ1≃−1.16204, σ2≃0.878198, σ3≃−2.35546, δ1≃1.74306, δ2≃−0.817295, δ3≃3.53319, λ1≃0.41898, λ2≃−0.060903, λ3≃−1.17773, ˉϕ1≃1.00000, ˉϕ2≃0.113338, ˉϕ3≃1.17773, ˉω1≃0.591136, ˉω2≃0.175009, ˉω3≃1.19823, ˉν1≃0.541872, ˉν2≃1.49758, ˉν3≃1.09837, Λ1≃0.031094, Λ2≃0.034096, Λ3≃0.134535, ˉΛ1≃0.000700, ˉΛ2≃0.002538, ˉΛ3≃0.012289.
Also, the conditions O1 and O2 are satisfied as we have,
and κ≈0.403605<1, where κ is defined in (O2). Hence, the conditions of Theorem (3.1) hold. Therefore, from conclusion of Theorem 3.1 the problem (3.16) has at least one solution on [0,1].
4.
Uniqueness of solutions
Next, we prove the uniqueness of solutions for the problem (1.6)-(1.7) via Banach fixed point theorem.
Theorem 4.1. Assume that f:[a,b]×R3⟶R is a continuous function such that,
Then the problem (1.6)-(1.7) has a unique solution on [a,b] if
where κ is defined in (O2) and ˉΔ is given by (3.12).
Proof. Setting supt∈[a,b]|f(t,0,0,0)|=N<∞, and selecting
we define Br∗={x∈A:‖x‖∗≤r∗}, and show that FBr∗⊂Br∗, where the operator F is defined by (3.3). For x∈Br∗, we use (4.1) to find that
where we used the norm given by (3.1).
Then, we have
Similarly, we have
Hence we have
Thus, Fx∈Br∗ for any x∈Br∗. Therefore, FBr∗⊂Br∗. Now, we show that F is a contraction. For x,y∈A and t∈[a,b], we obtain
In a similar mannar, we have
Consequently, we obtain ‖(Fx)−(Fy)‖∗≤(κ+3LˉΔ)‖x−y‖, which in view of (4.2) implies that the operator F is a contraction. Therefore, F has a unique fixed point, which corresponds to a unique solution of the problem (1.6)-(1.7) on [a,b]. This completes the proof.
Example 4.1. Consider the following fractional differential equation
t∈[0,1], supplemented with the boundary conditions of Example (3.1).
Obviously
Using the given data, we find that Δ≃0.134535 and ˉΔ≃0.012289, where Δ and ˉΔ are respectively given by (3.11) and (3.12). By the following inequality
we have L=112. Clearly (κ+3LˉΔ)≃0.406677<1. Therefore, the hypothesis of Theorem (4.1) is satisfied and consequently the problem (4.3) has a unique solution on [0,1].
Remark 4.1. Letting ξ=0 and μ=1 in the results of this paper, we obtain the ones for the fractional differential equation of the form:
supplemented with Riemann-Stieltjes integro-multipoint boundary conditions (1.7). In this case fixed point operator takes the form:
5.
Conclusions
We have proved the existence and uniqueness results for a multi-term Caputo fractional differential equation with nonlinearity depending upon the known function x together with its lower-order derivatives cDpax, cDp+1ax,0<p<1, complemented with Riemann-Stieltjes integro multipoint boundary conditions.
In Theorem 3.1, the existence of solutions for the given problem is established by means of Sadovskii fixed point theorem. The proof of this result is based on the idea of splitting the operator F into the sum of two operators F1 and F2 such that F1 is κ-contractive and F2 is compact. One can notice that the entire operator F is not required to be contractive. On the other hand, Theorem 4.1 deals with the existence of a unique solution of the given problem via Banach contraction mapping principle, in which the entire operator F is shown to be contractive. Thus, the linkage between contractive conditions imposed in Theorems 3.1 and 4.1 provides a precise estimate to pass onto a unique solution from the existence of a solution for the problem at hand.
As a special case, by letting ξ=0 and μ=1 in the results of this paper, we obtain the ones for the fractional differential equation of the form:
supplemented with Riemann-Stieltjes integro-multipoint boundary conditions (1.7). In this case, the fixed point operator (3.3) takes the following form:
In case we take αi=0 for all i=1,…,n−2, then our results correspond to the integral boundary conditions:
Acknowledgment
We thank the reviewers for their constructive remarks on our work.
Conflict of interest
All authors declare no conflicts of interest in this paper.













 DownLoad:
DownLoad: