Survey on security and privacy issues in cyber physical systems

1.   Introduction

Cyber-Physical system is a concept focusing on bridging physical and cyber worlds. Firstly, the term of CPS was proposed by National Scientific Foundation (NSF), where CPS are described as complex engineered systems devoted to integration of cyber and physical components to extend capabilities of recent embedded systems ^[1]. This definition states clearly that CPS is the next evolution stage of Embedded Systems. CPS while compared to embedded systems are not limited by just one device, it is more an ecosystem of devices operating in the physical environment and being controlled by computational elements. Another similarity to CPS concept is Internet of Things (IoT) which, from a conceptual point of view, can be considered as a subset of CPS encompassing the infrastructure connecting various physical and virtual entities called 'things' in order to provide advanced services ^[2].

In many areas of human activities, CPS has gained more and more attention, especially in the capacities where physical processes and physical equipment needed to be controlled, orchestrated and coordinated with humans, systems, or subsystems. The emerging trends like Industry 4.0 ^[3] or Industrial Internet ^[4] are the key indicators of CPS importance; transition to these concepts will involve increasing automation, autonomy and complete new understanding of production processes. Major incentive, which forces CPS development, is a need of convergence for physical processes and computational capabilities, where high degree of communication between components and abstraction of the processes occurring in the physical environment is needed. The scaling of the CPS systems, small and large scale respectively, is distinguished by number of involved components ^[5]. Small-scale CPS have just a little number of physical as well as cyber components and large-scale systems accordingly have hundreds or even thousands of components. Both of them can be geographically distributed, which may require convergence with global networks, such as Internet ^[6].

There were several efforts to develop a general model for CPS in order to give a clear idea of the main components of a CPS regardless of application domains. In ^[7], CPS is represented through three main layers: the first layer consists of sensors and actuators which observe changing physical environment; the second layer aims at communication and abstraction of the real world processes and the third deals with computational capabilities. Another work in ^[8] describes an approach for CPS design consisting of three layers, namely physical layer, platform layer, and computation/communication layer, where the last two layers are in fact cyber layers. To establish a comparison among the design concepts, there are common similarities such as the same number of design layers and similar functions performed by the layers. Thus, first layer in both concepts ^[7,8] is focused on physical components operating in physical environment, whereas the second layer is aimed at interconnection of the lower and higher levels, storage and service composition with particular attention being paid to abstraction mechanisms and the last one serves to high level functions such as computational algorithms, processing, etc. However there is some research work which purely focuses on architectures for specific application domains. As in ^[9], the four layer architecture for CPS in healthcare domain is represented.

Considering the complexity of modern CPS, issues of ensuring the security and safety of those systems are of high relevance. The potential threats can be related to a cyber, physical or both dimensions of CPS and thus require complex approach for identification and mitigation of security and safety vulnerabilities. In the current research the goal was to give an insight on vulnerabilities, attack types, mitigation schemes considering the CPS complexity in terms of scalability, distributiveness, components types and distinction between security and safety challenges. Special focus was made on Intrusion Detection Systems implementing the Machine Learning algorithms for threats detection and mitigation, with detailed literature research on algorithms and corresponding threats they were applied to, data sets and target objects which were investigated. Moreover, as the most of CPS can be described as open-loop systems, in other words, constantly collaborating with other systems, corresponding problems, issues and challenges are revealed and discussed.

The rest of the paper is organised as follows. Support technologies, timeline, Infrastructure and virtualisation concepts related to Cyber Physical Systems are presented in Section 2; whereas importance of security in the presence of existing threats is highlighted in Section 3. An account of threat mitigation techniques as well as threat modelling is presented in Section 4. Section 5 investigates safety aspects of cyber physical systems before open research issues are discussed in Section 6 and paper finally concluded in Section 7.

2.   CPS: all-encompassing

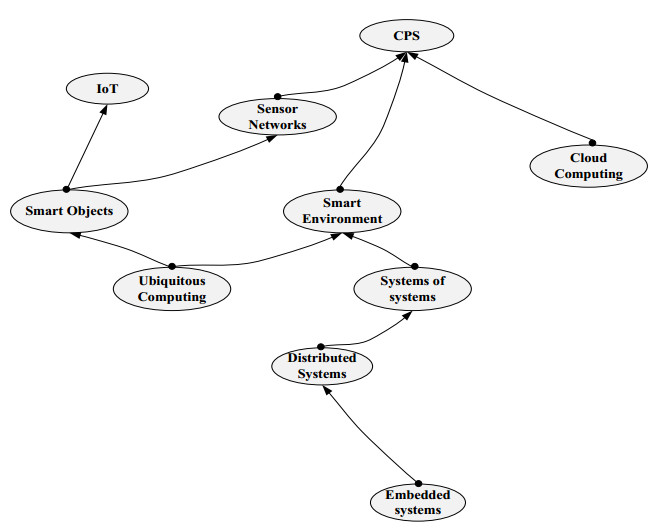
In this section the main technological developments are mapped as well as interrelations among CPS and other concepts are described to appreciate technological evolution chain which led to emergence of CPS. According to several sources, concepts such as Embedded Systems ^[5,10,11], IoT ^[5,10], Ubiquitous Computing ^[5,12], Smart Objects ^[5,13], Sensor Networks ^[5,14], Smart Environments ^[13,15] and Systems of Systems ^[15] plays an important role in CPS development and/or being an integral part of CPS.

2.1.   Support technologies

In terms of timeline, Embedded Systems are predecessors of all the mentioned concepts which appeared in the last century thereby starting the new era of microelectronics and responding on the critical issues, e.g. automatisation and remote control. Embedded systems have predefined functionality traversing across one or several functions, which cannot be easily changed (i.e. reprogrammed) by the end user. Importantly embedded systems were designed to control and manipulate the physical world processes ^[16]. Thus, initially embedded systems were narrow focused and compared to the IoT or CPS, were limited by just control functions of the physical processes without covering the cyber space.

With growing need to control and organize complex systems, the necessity for interactive embedded systems became clear and the notion of Networked Embedded Systems appeared. A notable work devoted to this topic was completed in the framework of RUNES project within a CORDIS framework. The scenario considered was a 'hybrid network composed of different joint subsystems' ^[17], in fact a system of systems. The most important factor pushing the appearance of CPS was transition from single systems to networked or connected systems of high complexity. Considering this trend, another important concept strongly influencing the modern CPS, namely Sensor Networks appeared in 80th. Typically Sensor Network consists of a set of sensors deployed in a certain area focussed on information gathering ^[18]. Appearance of Sensor Networks facilitated development of Smart Objects, which according to ^[19] are identified as items (sensors or actuators) consisting of microprocessor, communication facilities and power sources. However the sensor network is not considered as an independent unit, but just as a part of complex systems, as for instance fire monitoring system etc ^[20].

Huge influence on modern computing systems including CPS gave birth to concept of Ubiquitous Computing. Furthermore, the ideas of integration of computer systems with daily human activities making them 'invisible' for the end users were stated ^[21]. According to some researchers' opinion ^[22], ubiquitous computing overlaps with other concepts, for instance, ambient intelligence, IoT and pervasive computing. Another work in ^[23] states the main goal of IoT as provision of capabilities for the end users to extend current borders of everyday devices and development of personalized services by making use of connected ubiquitous devices. This represents the transition from Embedded Systems with predefined functionality to Ubiquitous Computing and IoT, where one of the main requirements is adoptability and agility. Further development of computing systems led to appearance of CPS and IoT. CPS is a step away from the paradigm where Operational Technologies are separated from Information technologies to prototype where physical and computational elements are highly integrated ^[14]. However, there is still no unified definition for IoT, some sources ^[24,25] describes IoT as a global infrastructure including communication technologies, standard protocols, etc., which provide services produced by 'things' to different high-level applications. While other sources ^[26,27] claim that IoT is a common term defining the sort of scenarios where the capabilities of smart devices/objects are boosted enabling global communication through internet and corresponding technologies. Thus, the idea of IoT can be considered as global term for representing the infrastructure for devices and systems to communicate or scenario where global connectivity is key requirement, while CPS finds itself in a first row of such a system, which can also be distributed and comprise global connectivity, but also be self-sufficient as a unit. Figure 1 demonstrates CPS support technologies.

Figure 1.  CPS support technologies.

DownLoad: Full-Size Img PowerPoint

2.2.   Infrastructure

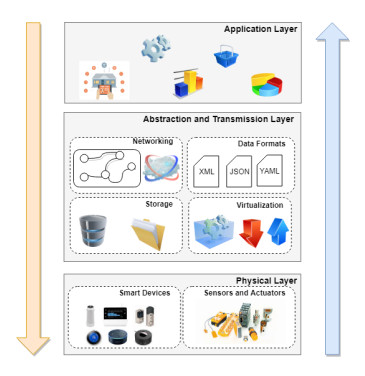
Infrastructure plays a crucial role in deployment of every system; the same applies to Cyber-Physical Systems (CPS). As the main components of CPS can be considered as sensors / actuators, controllers, communication networks ^[28]. However, some CPS solutions additionally employ gateways ^[29]. Importantly, CPS can be both open-loop or closed loop systems. By the analogy with Internet of Things (IoT), open-loop CPS can have access to the global networks, and in this case such paradigms as Cloud Computing, Big Data etc. can be added into the notion of CPS infrastructure. Cyber Physical systems can consist of large extent of heterogeneous devices, including sensors, actuators, etc. Accordingly, this also puts some restrictions on CPS, for instance, necessity of using energy safety protocols and communication technologies. This heterogeneity is one of the biggest challenges in CPS, since various types of devices should get support from a system. Considering modern challenges in big as well as small systems, among challenges such as seamless integrity etc, mobility is another of most important factors that influences the whole system. It means that migrating devices can cause several difficulties and needs to be taken into account in the normal functionality of the system. Figure 2 shows generalised CPS infrastructure.

Figure 2.  Generalised CPS infrastructure.

DownLoad: Full-Size Img PowerPoint

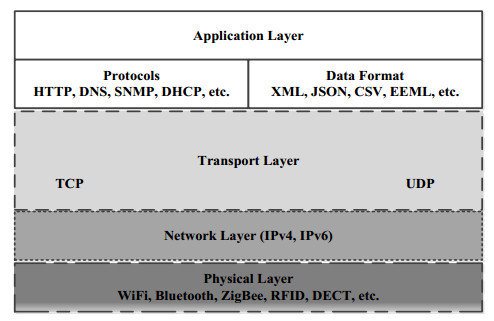
Infrastructure is a complex term which includes hardware as well as software components. Since CPS are complex engineering architectures encapsulating physical and cyber spaces, several attempts for structuring them have been made. Five level CPS architecture has been proposed in ^[30] with layers functionality described as: (ⅰ) Smart connection level, (ⅱ) Data-to-information conversion level, (ⅲ) Cyber level, (ⅳ) Cognition level, and (ⅴ) Configuration level. Crucial role by different architectural solutions plays the point of view on the system, for example in ^[31], CPS architecture is proposed from the service oriented point of view and consists of 4 levels as follows: (1) Perceive tier, (2) Data tier, (3) Service tier, and (4) Execution tier. Since CPSs are the part of ICT area, it is important to find interrelations between Open Systems Interconnection Model (OSI), architectures and models developed for CPS. An adapted OSI model for CPS involves Middleware and System Infrastructure model. However, if CPS needs to be integrated with global networks such as Internet, TCP/IP model can be the best contender, where two lowest layers, Physical and Data accordingly, are represented by just one level. Application, Transport and Network layers respectively form part of the other three layers. Figure 3 represents some technologies and protocols belonging to each of the layers.

Figure 3.  TCP/IP enabled CPS integration model.

DownLoad: Full-Size Img PowerPoint

2.3.   Virtualisation in CPS

The main task of virtualisation in the context of CPS is to hide or abstract technical details from the layers lying above and to allow flexible resource sharing, so that functionality or resources are provided as a service. Since CPS connect cyber and physical space and include the whole cycle from the signals to complex applications, some important types of virtualisation schemes are described below.

2.3.1.   Network virtualisation

Network Virtualisation is a complex term and can be divided into several subsections, (ⅰ) Network Interface Cards virtualisation (NICV), (ⅱ) Router virtualization, and (ⅲ) Link virtualisation ^[32]. NICV relies on giving shared access to the network interface, for example Virtual Machine, where the VM Monitor not only provides access of each VM to the common network interface, but also protects from accessing data of each other ^[33]. Router virtualisation concept allows deployment of several virtual networks on the same physical infrastructure, thus creating isolated partitions ^[34]. Several virtual routers can be created on one hardware platform, for example XEN platform mentioned in ^[35]. Link virtualisation contains main concepts of physical channel multiplexing, bandwidth virtualisation and data path virtualisation ^[36,37]. Bandwidth virtualisation aims at union of several bandwidths to create a virtual link whereas link virtualisation is data path virtualisation with manipulations performed on packets, for example tunnel based VPNs and tags based VLANs ^[38].

2.3.2.   Devices / Resource virtualisation

Devices / Resource virtualisation involve representation of physical resources without binding to their specific way of access ^[39]. In other words the main purpose of device virtualisation is to create a digital representation of device or object in cyber space considering all the necessary data which is able to access it and to represent its resources in the context of Service Oriented Architecture (SOA) ^[40]. These devices and objects can also have a variety of identification mechanisms like virtual personality or virtual identity ^[41]. Moreover, as CPS may not always possess the necessary capabilities to perform certain tasks, in this context resource virtualisation can be used as a flexible tool for collaboration, namely to share some tasks with nearby CPS with required resources ^[42,43].

2.3.3.   Applications virtualisation

Applications virtualisation is of particular importance aimed at representing software applications abstracted from the underlying hardware or software platform ^[44]. Data Distribution Service (DDS) protocol provides the virtual environment for publishing and subscribing applications ^[45]. In the context of requests and relationships relevant to an application, the concept has been employed in database virtualisation to address the challenges of repeatability, re-execution without approach towards the database ^[46]. There are also attempts to implement virtualisation for specific application domains, where focus is made on quality monitoring ^[47,48]. Virtualisation in B2B and manufacturing domain is employed by usage of cloud computing ^[49,50].

2.4.   Distributed systems

Many of the CPS can be considered as distributed systems, as they have dispersed components both on physical and computational level. A good example could be set of sensors deployed in a certain space connected to an agammaegator. Data collected from these sensors is stored in a distributed way and services built upon theses sensors, even deployed on the same infrastructure, operate in request/reply fashion. Distributed systems set a number of difficulties, such as synchronisation and collaboration; security is also a matter of concerns since in large scale system, messages are vulnerable on the way among nodes. Nevertheless, as modern CPS contains many components, which can be considered as independent units, thus issues of collaborative behavior are of the main importance. Distributed storage is a concept which is especially relevant for CPS producing huge amounts of data. Challenges arise such as local storage of the data which is harvested from the sensor nodes. Sensing nodes have some restriction in memory capacity etc, thus they need to clear memory and store the data in a centralized way. This can create a set of difficulties, for instance if connection is dropped and the data are extremely important for the functioning of the whole system. One of the storage implementations is Backend Device Management Generic Enabler provided by Fiware platform ^[51]. Another solution from the IoT perspective represented in ^[52] is based on collaborative distributed way of storing data, when data in the nodes memory are replicated and distributed to neighbor nodes with available memory capabilities, which are constantly updated according to a memory status in a given moment. Thus, distributed storage is relevant not only for large scale CPS, but also for small sensor networks with real-time restrictions or/and increased reliability.

Distributed or parallel processing is another relevant concept for the CPS. For CPS with real-time constraints or generating large amounts of data, it is important to process gathered data in a fastest way and create interdependencies among various events. In this context two emerging concepts of distributed IoT applications and Federated Learning need to be mentioned. Distributed IoT is an application where components are deployed near the data sources ^[53] and might be executed in different platforms ^[54]. This concept is very similar to the Federated Learning which assumes that data are processed in a distributed way on mobile devices providing a model which is being used to build a general exemplary encapsulating a set of measurements performed by the nodes ^[55,56]. In the context of CPS, Federated Learning can be applied for processing data locally thereby reducing the load on a central node.

3.   Security in cyber-physical systems

Since potential threats can affect both the cyber and physical environments, security provision in CPS is extremely important at all stages, namely design, deployment and operation ^[57,58,59]. Moreover, as CPS are used on many objects of critical infrastructure, issues for protecting them have become extremely relevant. Distributed nature is another concern to be considered while introducing the security and safety measures during the design of CPS design phase. One possible view point is when the complex CPS is represented as a peer-to-peer network with key nodes with computational capabilities serving as gateways or access nodes for local CPS segments ^[60]. In the proposed architecture security tasks are performed by a "control element" having the role of security administrator implementing the external or intermediate (among distributed components within CPS) security policy for the CPS. Besides the external security policy issues of internal security policy management and conflict resolution are to be considered, as in ^[61], where the system for critical infrastructure protection, namely hydroelectric dam, is represented. The work discusses analysis of unauthorized network usage and proposes corresponding countermeasures which include reconfiguration of devices as well as measures ensuring integrity of critical data storage. The objects and people are represented as assets and agents respectively in Socio-CPS (SCPS). Though the issues related to SCPS security are discussed in ^[62], however the work presented lacks in attack prediction. Modern cyber physical systems require components- or subsystems-centric security approach to evaluate the possible consequences for the whole system, even when one of the components is compromised ^[63]. Considerable amount of research works discusses the possibility of attacks on control systems in order to gain access to the physical part of CPS ^[64,65]. This fact can be clearly seen on example of SCADA systems, design principles of which were introduced before the era of global interconnected systems ^[66]. As a consequence, SCADA systems, even though based on web technologies, often have compatibility issues related to integration with modern corporate communication networks. Further consequences associated with convergence of SCADA systems with corporate and global networks are the variety of new security threats, such as non secure remote connections, knowledge availability etc ^[67], thus with regard to the previous point the access of third parties providing maintenance services need to be restricted in terms of privileges to perform changes within a system ^[68]. Centralised administration has been proposed to tackle the issue of insecurity in remote connections ^[69] as well as unauthorised privileges. For further chapters we partially adopted the Security Framework ^[70] aiming at giving an insight on the area of CPS Security. It comprises of three dimensions or three coordinate axis: security, systems and CPS components respectively. Important deliverables of this framework is division of CPS components on physical, cyber and hybrid having both cyber and physical parts and security dimension introducing the notions of attack, vulnerability, control and threat. However, the framework doesn't represent the threats mitigation schemes, approaches and methods, focusing only on threats themselves and pays less attention to safety mentioning this as a part of security.

3.1.   Types of existing attacks

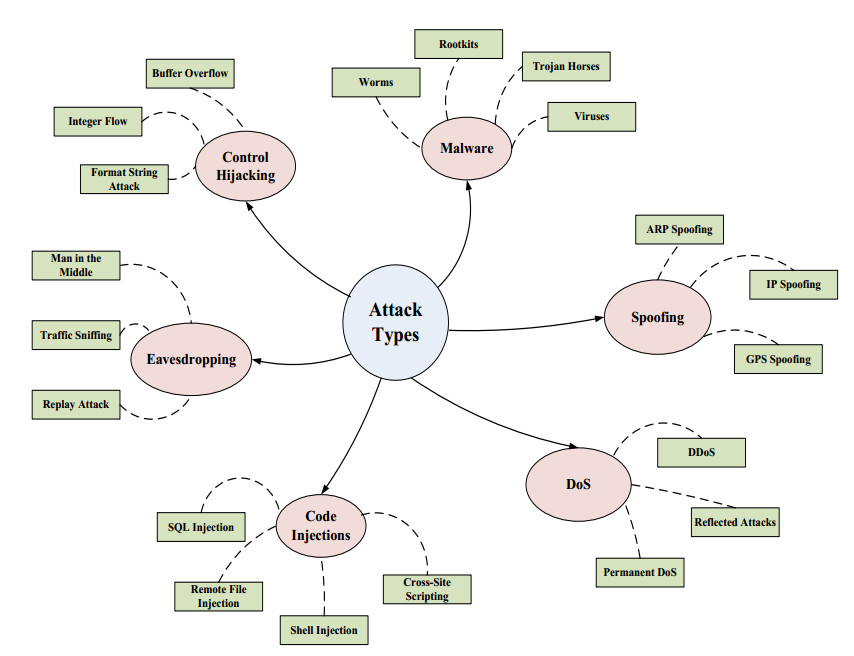
Figure 4 describes common attack types and their sub-types in Cyber Physical Systems. The intruder aims to take control of entire system by launching control hijacking attack, whereas code injection exploits system vulnerabilities by systematic injection of rogue piece of code to change the execution of the entire program. Malware attacks employ special software to hamper normal functioning of a system. Traffic sniffing or interception is practiced in case of eavesdropping attack, whereas the intruder impersonates itself in spoofing attack ^[71]. All attack types can be extended by Denial of service attacks (DoS) which is aimed at flooding the system in order to disable the actual services provided by the system ^[72].

Figure 4.  CPS security: common attack types/subtypes.

DownLoad: Full-Size Img PowerPoint

Based on the above mentioned attack types several attack subtypes can be highlighted as follows.

3.1.1.   DoS subtypes

Permanent DoS is a type of attack when intruder tries to exploit unpatched vulnerabilities in order to install modified firmware to damage a system ^[73]. Distributed DoS attack is based on a model when several nodes/systems are sending requests to a victim system trying to occupy the available resources (i.e. bandwidth, processor time, etc.), thus rendering the system unable to provide services. Intruder employs the broadcast address of ill-configured network and sends packet by replacing its own address with the victim node address in reflected attacks. Thus the victim node eventually is flooded with fake responses. Smurf attack (ICMP packets) and Fraggle attack (UDP packets) are some of the variations of reflected attacks.

3.1.2.   Spoofing subtypes

GPS spoofing is based on broadcasting of incorrect signals of higher strength than received from satellites in order to deceive the victim ^[74]. Intruder explores the IP addresses of the victim nodes and then sends ARP responses to node X and node Y, with IP address of corresponding node and its own MAC address in ARP spoofing. Thus all packets between X and Y will then pass through the intruder node. IP spoofing is another subtype of spoofing attack aimed at using another IP address to pass through security system. This type of attack can be used on the first stage of complex intrusion in conjunction with reflected attack.

3.1.3.   Code injection subtypes

SQL injection attack involves insertion of malicious SQL statement in the queries, thus leading towards failure of the input data. Cross site scripting exploits open scripting vulnerabilities and adds malicious code into web application leading towards execution. Remote file injection extends itself on the serve side of web applications where the file with malicious code is downloaded and is executed on the server. Shell injection attack is implemented through inclusion of malicious shell code into the code string for further interpretation by the shell ^[75].

3.1.4.   Eavesdropping subtypes

Man-in-the-Middle is an active type of attack and occurs when intruder intervenes between communicating entities trying to intercept the packets. Traffic sniffing is a passive type of eavesdropping aimed at traffic analysis using special device or program. Relay attacks are aimed at interception of authentication related information.

3.1.5.   Malware subtypes

Worm is a type of Malware software with ability of making copies of itself thus resulting into wastage of network bandwidth. Virus is also able to replicate itself as worm, but comparatively infects files and programs in the system. Trojan horse intrudes in the system under the guise of legitimate software, whereas Rootkit is a set of software; such as scripts, executable files, configuration files, etc; with ability to hide itself and other malicious software.

3.1.6.   Control hijacking subtypes

Buffer overflow is a phenomenon when a program is writing data outside of the given buffer, often it is the consequence of the wrong processing of input data. Integer overflow is an error occurred due to inability to represent the numeric value within given storage space, whereas Format string is an intrusion during which the input string is executed as a command.

Importantly, all attack types can be divided into either passive/active or invasive / non-invasive respectively ^[76]. Passive attacks, such as traffic sniffing, have the purpose to intercept the sensitive data without causing any destruction to the operation of the entire system. Whereas active attacks, like DoS/DDoS, code injections etc, are aimed at causing direct damage or to gain the control of the system or infrastructure ^[77]. These two paradigms are completely different, as for passive type of attacks it is desirable to be invisible to security tools to be able to continue dangerous activities as long as possible. The attacks, which are intended to remain invisible for a victim system, are often described in the literature as stealth attacks ^[78]. For active attacks, main purpose is to destroy or damage the system. Depending on the above mentioned attack groups, accordingly different protection strategies need to be implemented.

3.2.   Attack vectors

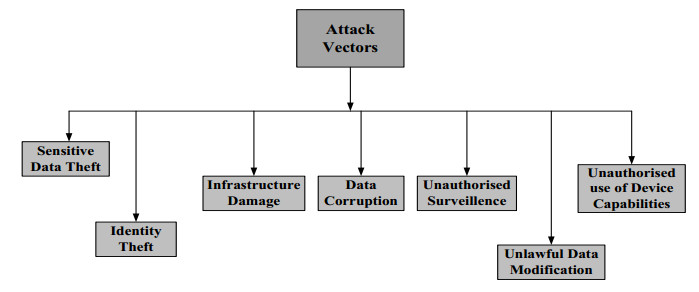
Threats eventually translate into attack vectors. Hardware based attack vectors for smart devices, namely device identity theft and cryptographic keys theft have been identified in ^[79,80,81]. Importantly, attack vectors can vary depending upon CPS application domain. Work presented in ^[82] considers medical implants related attacks with the purpose, either to steal the information, change the therapy, or render the device useless by exhaustion of its energy sources. In the energy management domain, for example smart homes, an intruder can manipulate energy consumption measurements resulting into energy theft ^[83]. Considerable research work has been done towards automatic identification of attack vectors, such as data disclosure and resources disruption etc ^[84]. Knowledge based attack vector presented in ^[85] assumes that the intruder may not possess the necessary knowledge about physical processes and ways to take control over the system. However, the attacker implements five steps of intrusion: access, discovery, control, damage and cleanup accordingly, to gain full control of the system in direct or indirect way and to hide any traces of any caused intrusion. Figure 5 presents the main attack vectors in Cyber Physical Systems.

Figure 5.  Attack vectors in cyber physical systems.

DownLoad: Full-Size Img PowerPoint

4.   Threat mitigation schemes

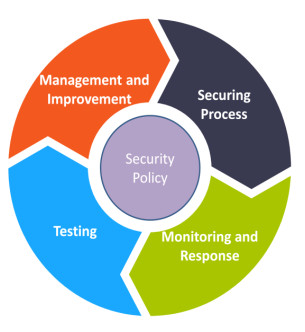
Classical approaches in security assurance are often concentrated on the whole system paying less attention to a subsystem/component security. It is very important to distinguish the system faults from intrusion or attack. In this context, vulnerabilities assessment approach for industrial systems in proposed in ^[86]. In this context, a multi-agent scheme for identification and detection of attacks on smart grids is presented in ^[87]. The process of attack and faults separation is supported by condition state monitor analysing collected logs and system information. The Issue of avalanche effect in complex systems was raised in ^[88], when affecting one element or a subsystem can have the consequences for the entire system. However, the general methodology (Figure 6) to secure network and services infrastructure was proposed by CISCO ^[89], contains the following elements: security policy, securing process, monitoring and response, testing, management, and improvement. Securing Process applies to procedures of conducting necessary measures according to a valid security policy. Monitoring and Response implies to a permanent knowledge extraction about the environment where the system is deployed. Testing phase involves constant checking of the system abilities to react on threats including time-to response parameters. Lastly Management and improvement stage is aimed at organizing and efficient use of security assets with further activities on identified security gaps.

Figure 6.  CISCO security methodology.

DownLoad: Full-Size Img PowerPoint

The key element of security methodology is Security Policy (SP) directly affecting other components. Well established security policy should define following aspects ^[90]:

● The set of measures to undertake in the case of particular threat

● Roles distribution

● Clear definition of what is the accepted behavior

● Resources classification based on their sensitivity

● Communication process organization

● Reporting and logging process organization

Securing process assumes establishment of all relevant security measures such as firewalls, authentication, authorization etc. Monitoring and response are focused on mechanisms for observing and detecting threats combining hardware, software and human practices. Testing serves to the purposes of constant control of configuration and state of the security system helping in detecting weak points. Managing and improving, as the new threats appear, security system needs to be kept up to date and management assumes keeping proper functioning of the system over time.

This work focuses on analysis of vulnerabilities occurring through the interaction of cyber and physical elements of a system using discrete approach. Some salient and diverse threat mitigation schemes for Cyber Physical Systems are proposed in the sections below.

4.1.   Intrusion detection systems

Intrusion detection system (IDS) is an important component of cyber security systems which is aimed to inform either operator or a cyber security enabled system to respond to an attack. The main functions of IDS in CPS consist of collecting data related to entity which has been compromised and subsequent analysis of gathered data ^[91]. National Institute of Standards and Technology proposes four main types of IDS, most of the modern IDS types belongs to one of these types ^[92]:

● Network-based – focusing on network traffic and corresponding threats considering network protocols, traffic, devices.

● Wireless – is similar to the first one; however wireless traffic, protocols are in the scope of those IDSs.

● Network behavior analysis – monitors network traffic flows identifying suspicious behavior patterns and policy violations.

● Host-based IDS are monitoring activities related to a certain host including traffic, application activities, operations on files and configuration activities. This type of IDs is often applied on critical infrastructure nodes.

In terms of the way of detecting the threat modern IDS can be subsequently divided into three subetaoups ^[93]:

● Anomaly-based assumes detection of the behavioral patterns which are different from the patterns of normal system's functioning;

● Signature-based requires a storage with a set of threats models being kept up-to-date, used to identify threats;

● Specification-based, in this mode specifications of the system as whole, as well as of components and interfaces are utilized for detection of suspicious activities.

However different way of IDSs classification was proposed in ^[91], where IDS are grouped based on audit material, namely: host or network and detection techniques: knowledge based or behavior-based. Furthermore, the same work provides the explanation if difference between usual IDSs and IDSs for Cyber-Physical systems.

Scheduling techniques have been proposed to address the issue of resource constraint of CPS where responsibilities sharing among CPS nodes are established to provide constant processing flow ^[94]. The approach presented in ^[95] employs guaranteed secure sensors to provide high probability that attack will be detected. Usage of so called trusted devices' compares data gathered from reference device with the data gathered by other devices deployed in the same environment. This idea has found its implementation in ^[96], where it is assumed that a set of sensors measures the same physical variable. The next step in this technique involves gathering the measurements and analyze using sensor algorithm considering the predefined sensor precisions. However, this idea is not very practical and may give in to passive as well as DoS type of attacks. Time based detection which assumes that there is a predetermined variable for worst case execution time (WCET), is another possible approach of intrusion detection in CPS ^[97]. If the execution time exceeds the predefined limits, then the system is assumed compromised.

4.2.   Machine learning, threshold and rule based schemes

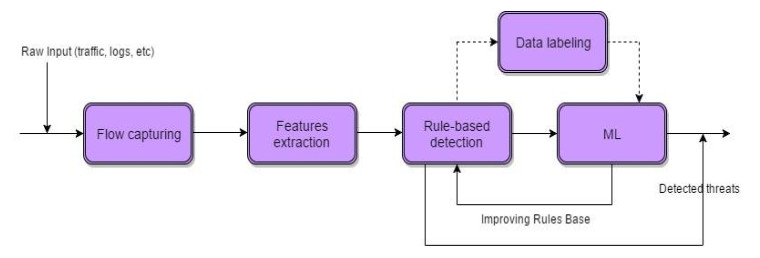
It is important to distinguish between simple rule-based mechanisms and machine learning algorithms (ML). Both can be represented at the same time in the same security architecture. Rule-based mechanisms are used as the first barrier on the way of threats identifying the critical threats which can cause significant destruction for the system and are based on rules from previously extracted knowledge. Security architecture combining ML algorithms and rule-based mechanisms consist of some basic phases: features extraction, features selection, rule-based detection and ML algorithms for threats detection and extraction of new rules (Figure 7). More advanced approach presumes addition of human supervision to the security architecture, supplied by extracted knowledge from the machine-learning module ^[98].

Figure 7.  Hybrid rule-based and ML approach.

DownLoad: Full-Size Img PowerPoint

The raw input can be represented by packets, log files which is captured and analyzed, for instance priority could be given to specific traffic types like P2P. The second step presumes definition of key features which are relevant for threat detection. On the third step, rule-based mechanisms are applied to the set of key features and potential dangerous entities are discarded. After malicious entities identified by rule-based detection module are discarded and the learning set for the ML module is formed, other entities, not identified as malicious, are checked by ML module. Furthermore, ML module can contain rule inference modules to produce new rules based on the new faced threats.

It is worth to mention that machine-learning algorithms can be divided into two general groups, namely supervised and unsupervised. Supervised learning or so called stimulus-reaction is based on a set of learning samples as input and desired outputs, then the mapping functions is produced to connect the input and the output values. In the case of unsupervised learning there is just an input value and the task of an algorithm is to describe the structure from unlabeled data. The most common problems of supervised learning are classification and regression, and of unsupervised clustering, and association. In the context of system security clear example of supervised, unsupervised and semi-supervised approaches could be a set of detected threats. Machine learning techniques for traffic classification using ML were raised and discussed in ^[99]. The first case when supervised approach can be applied is when the system has knowledgebase with characteristics of main dangers, thus the set of malicious events as an input can be classified into predefined classes: DoS, spoofing, malware, etc. The second case of unsupervised learning is when no predefined descriptions of faced threats are available, but the threats need to be grouped based on certain similarities. And semi-supervised learning is for example, when the input set contains some labeled data for instance some of detected events belong to DoS domain, but the rest of the cases are not identified or the attack type is known, but its modification/subtype is completely new for security system.

A Framework based on Machine learning, threshold based and rule based outlier detection to provide security in CPS for energy management systems (EMS) is proposed in ^[100]. Machine-learning approaches compensate for intrusion detection through deviation in system behaviour. Mostly these approaches require defining groups of devices or subsystems, where each subsystem may have its own behaviour pattern. Threshold-based-outlier approaches cater towards data analysis which may exceed the predefined limits. Rule-based detection analyses gathered sensor data on conformity with physical laws and remain within statistical limits. Even though threshold based and rule based approaches are not well suited to detect passive types of attack, but in conjunction with machine-learning, enable them to analyse the whole system behavior even when the data remains within set boarders. Deviations or anomaly based detection is employed to detect attacks on SCADA systems in ^[101].

Machine learning algorithms can be applied on different levels of system security, as for instance on network ^{[102,103,104]} or application ^[105,106]. Issues of Software Defined Networks security were raised in ^[107], where some important threats were identified and solution based on Hidden Markov Model was proposed. The classification problem of incoming packets on dangerous and normal was discussed in ^[103] and multilayer perceptron algorithm was applied. Another work ^[108] was devoted to applying ML for comparison of several network traffic features extractors in order to define efficiency of botnet packet detection with perspective of defining the weight of each feature.

Some important and widely used ML algorithms for insecurity assurance are as follows ^[109]: Random forest, Naïve Bayes, Bayesian Network, Logistic regression, Sequential minimal optimization, AdaBoost. The list can be completed with following ML algorithms used for detection of Web Spam: Support Vector Machine, Multilayer Perceptron Neural Network, Random Forest, K-nearest neighbor, Bagging, Dagging, Rotation Forest and Boosting algorithms. The above mentioned algorithms can be classified in two large groups (Table 1), namely single and meta algorithms ^[110]. Distinguishing characteristic of the Meta-algorithms is agammaegation of simple or so called 'weak' classifiers and creation of a 'strong classifier' combining them. For instance Boosting algorithm belongs to supervised learning algorithms combining single supervised algorithms such as Support Vector Machine or Naïve Bayes and is often applied for classification problem solving. More detailed research of ML methods and their application in security domain can be found in ^[111].

Table 1.  ML algorithms.

ML algorithms	Meta ML algorithms
Decision Tree	Bagging
Logistic Regression	Boosting
Naïve Bayes	Dagging (Weka)
KNN	Rotation Forest
Neural Networks	Random Forest
Support Vector Machine
Bayesian Network
Genetic Algorithms
Sequential Minimal Optimization

---

 | Show Table

DownLoad: CSV

Table 2 presents a detailed set of relevant work in the area of ML applied for security purposes. All above mentioned algorithms are organized based on several criteria such as data set, type of ML algorithm, threats types and objects of analysis.

Table 2.  Summary of ML algorithms, data sets, threats and investigated entities.

	Algorithms	Palenzuela et al., [103]	Leeds and Atkison, [149]	Suh-Lee et al., [150]	Morales-Ortega et al., [151]	Hu et al., [152]	Gouveia and Correia, [153]	DeLoach et al., [105]	Kamarudin et al., [154]	Chinchore et al., [102]	Livadas et al., [104]	Alshammari and Zincir-Heywood, [155]	Li and Guo, [156]	Wang et al., [157]	Baig et al., [158]	Farid et al., [159]	Stein et al., [160]	Raj Kumar and Selvakumar, [161]	Hu et al., [162]	Laskov et al., [163]	Yerima et al., 2015	Zhang et al., [164]	Syarif et al., [165]
Single ML Algorithms	Decision Tree						x			x	x	x				x	x				x		x
	Logistic Regression						x	x	x												x
	Naïve Bayes										x					x					x		x
	KNN												x
	Neural Networks	x	x				x
	Support Vector Machine			x		x														x
	Bayesian Network										x
	Genetic Algorithms																x
	Sequential Minimal Optimization
	Random Tree				x
	BIRCH																					x
Meta ML	Bagging																	x					x
	Boosting						x					x		x	x			x	x				x
	Random Forest																				x
Data Set	Andrototal.org		x
	SKAION 2006			x
	DREBIN				x
	DARPA					x			x
	UNB ISCX						x
	PlayDrone							x
	VirusShare							x
	Arbor Networks							x
	Infocom06									x
	Dartmouth's wireless campus network										x
	Univ2007 Dalhousie University											x
	Univ2010 Dalhousie University											x
	KDD99	x											x		x	x	x	x	x	x
	WEBSPAM-UK2006													x
	Conficker																	x
	UNINA																	x
	SSE Lab																	x
	CAIDA DDoS																	x
	McAfee's internal repository																				x
	Self acquired data set																					x
	NSL-KDD																						x
	IARPA Dataset			x
Threat	Probe						x						x			x	x		x	x			x
	DOS						x						x		x	x	x		x	x			x
	U2R						x		x				x		x	x	x		x	x			x
	R2L						x		x				x		x	x	x		x	x			x
	Spam													x
	DDoS																	x
	Flooding																	x
	Maleware				x																x
	Botnet traffic identification										x											x
	VoIP malicious traffic identification											x
	Sybil attack									x
	Malicious applications		x					x
	Buffer overflow					x
	Malicious data in messages			x
	Network intrusion	x
Object of analysis	benchmark labeled data															x	x	x	x	x			x
	Applications featured logs							x													x
	network traffic traces										x	x						x
	TCP dump files												x		x			x
	pcap files																	x
	Human-assigned labels (spam/nonspam)													x
	mobility traces									x
	BSM audit logs					x
	Binary vector				x
	Log files		x	x
	traffic/packets	x

---

 | Show Table

DownLoad: CSV

4.3.   Knowledge based schemes

With constant development and improvement of malwares and intrusion techniques, there is a need for continuous update of the database of protection systems. Development of approaches for collecting and integrating knowledge about new threats with limited expert involvement is very important. The knowledge based approaches analyse unlabelled data of the malwares; based on them classifies the type of malware by referring it to one of the established and well known clusters. Knowledge based structural health monitoring techniques are applied to malware detection in ^[112]. The presented work also states important requirements for attack detection in manufacturing where no or little interference with normal functioning of a system is being made.

4.4.   Threat mitigation and modelling

CPS modelling holds a crucial role and it involves requirements of heterogeneity, dynamism and complexity which must be adequately considered and met accordingly ^[113]. The CPS modelling can span from information transfer to processes modelling ^[114]. In this context, security approaches in terms of threat modelling, strategies planning and unified approach to treat security and safety issues together are discussed in ^[115]. However independent of the model types, some issues are applicable for all the models. The model should be determinate, able enough to help arrive at solution of the problem, provable and executable ^[116].

According to ^[117] there are five common modelling approaches which can be applied to a complex system: System dynamics, Bayesian networks, Coupled component models, Agent-based models and Knowledge-based models. System dynamics is an approach to analyze the whole system over certain periods of time, where all system components interact through the feedback loop; in this way change in behavior of one component can affect the other components and as a result the whole system. Bayesian network is aimed at defining the influence of one entity characteristics on another entity characteristics or one event on another. Whereas coupled component modelling approach is about using the models or model components from different disciplines in order to achieve an integrated solution ^[117,118]. In the agent based modeling, all entities of the system are represented through interacting agents with specific behavior considering their influence on the whole system. Finally, the knowledge-based modelling uses knowledge base and the logic tools to extract solution.

Several efforts have been made towards security modeling of the cyber physical systems. A model is presented in ^[119] with the focus to combine cyber and physical threats of a critical infrastructure. Attention is also paid towards identification of features which have to be protected according to the predefined trend of security policy. Complex approach of security modelling in CPS which involves merger of cyber threats with physical threats is discussed n ^[120]. The modelled scenario employs UML and Sequence diagrams with application in transportation domain, e.g. in railroad management. The same idea is discussed in ^[121] which represent an analysis of information flow from perspective of integration of physical and cyber space. Importantly, the combination of cyber and physical characteristics can protect as well as endanger the information flow. Research presented in ^[122] discusses several attack type models such as fuzzy, interruption, man-in-the middle, replay, overflow and down-sampling attack models. The presented models were tested in a scenario which involved electrical vehicle design in order to show and analyse the behaviour of a system. Research work has also focussed on vulnerability assessment modelling methods which involve attack vectors such as: falsifying sensor inputs, changing set points and sending harmful commands to different system components. The methodology often is based on the interacting agents approach aimed at detecting malicious agent actions and possible consequences for the system state. However, agent-based approach could be applied to members of CPS, as in ^[123] the problem of formation control under attack in multi-agent systems was stated. CPS components are represented through agents who are under DoS attack, considering two scenarios when one agent or all agents are under attack. Another work presents Ariadne tool for modelling security requirements with topology of operational environment ^[124]. This method assumes that movement of agents and assets is considered in terms of satisfaction of security requirements, possible violations and subsequent verification.

Table 3 summarizes mentioned threat mitigation techniques, in the context of adopted approach, purpose and type of attack as well as application domain.

Table 3.  Threat mitigation techniques comparative analysis.

Research Work	Attack Purpose	Type of Attack	Proposed Approach	Target	Application Domain
Zimmer et al., [97]	Sensors compromise	Active	Time-based detection	Node		General
Nur Abdullah and Tozal, [72]	Denial of service	Active	Route record of IP protocol, Probabilistic packet marking	Network		General
Al-Hammadi and Aickelin, [142]	Data stealing, Denial of Service	Active, Passive	Behaviour analysis	Network		General
Ivanov et al., [96]	Sensors compromise	Active	Data fusion from sensors	Node		Robotics
Skormin et al., [144]	Variety of attacks as well as system failure	Active, Passive	System behaviour analysis based on system call data	Node, Network		General (e.g Health monitoring)
Ntalampiras, [81]	Sensors compromise	Active	Characteristics fusion of diverse signals representation	Network		Smart Grid
Huda et al., [112]	Injection of junk code, Instructions re-organisation, code substitution	Active, Passive	Dynamic changes in malware attack patterns based on unlabelled data	Node		General
Petrovski et al., [143]	Variety of attacks	Active, Passive	System behaviour analysis	Node		Automotive
Rahman et al., [87]	Data replacement, information corruption, Instructions re-organisation	Active, Passive	Agent-based approach	Network, Node		Energy Management
Steger et al., [88]	Taking control over system	Active	Metric-based approach for parameters of components/subsystems	Node		Automotive
Udd et al., [101]	Data replacement, information corruption, Instructions re-organisation	Active, Passive	System anomalies analysis, timing analysis	Node, Network		SCADA Systems
Adhikari et al., [141]	Code injection, Sensors compromise	Active, Passive	Analysis of causal relationship among devices	Node, Network		Power Systems
Vincent et al., [57]	Taking control over system	Active	Behaviour analysis	Node		Manufacturing
Paridari et al., [100]	Denial of service	Active	Machine learning detection, limit-based detection, rules-based detection	Network		Energy Management

---

 | Show Table

DownLoad: CSV

5.   Safety in cyber-physical systems

Dynamical nature of the cyber-physical systems set important requirements for security systems and analysis. Work presented in ^[58] employs system Theoretic Process Analysis (STPA-sec) to monitor systems security and STPA for smart grid safety analysis. Most importantly, the presented work highlights that security and safety need to be considered jointly in order to identify the most complete set of cases which can lead to a system threat. In order to set clear line between two notions, security and safety, there is a need to highlight the differences. According to ^[125], safety and security has many features in common, but the main difference is in the nature of problems covered by the terms. In the case of security, threats might be unknown and system or analysts have to act under higher level of uncertainty. On the other hand, safety hazards scenarios can be easily formulated from the restricted set of threats and reports based on previously faced hazards. Bayesian Belief Networks were used in ^[126] in order to analyse safety in conjunction with security. Moreover, data obtained using the Bayesian Belief Networks approach were compared to data gathered through Functional Requirements approach with conclusion made that they can complement each other.

Due to distributed and multi layered nature of the CPS, where components or subsystems can be deployed on different geographical locations, safety issues of communication among entities have become extremely important. An approach for safety assurance in the presence of unreliable communication has been presented in ^[127]. The presented scheme is based on safety intervals for message arrival and considers system evolution in the case of unlimited delays. Dimensional view on CPS safety analysis, where domain model introduced is divided into abstraction levels, viewpoints and modes is presented in ^[128]. The highest abstraction level in this work describes physical processes and communication with physical environment which includes users. The cyber level is responsible for division of a CPS into subsystems and processes into sub-processes. The next level aims at division of subsystems into components and sub-processes into process steps. Subsequently, the last layer, i.e. component layer, sets the modules considering the purpose of components. Viewpoints defines the safety consideration point, in other words it allows to split the general problem of safety provision in CPS onto specific blocks related to structure, behavior, communication, deployment or physical aspects.

Safety critical cyber physical systems can suffer from sufficient financial loss due to incorrect usage or an intrusion, thus rendering the system not usable ^[129,130]. CPS deployed on critical infrastructure, for instance energy generation, medical CPS, industrial CPS is good example of safety critical systems. Safety-critical systems possess a number of requirements including: feedback loop from physical environment, distributed management and control, functioning under uncertainty, real-time etc ^[131]. Spatial and temporal characteristics are very important, thus requiring urgent decision making in emergency situation in case of safety-critical systems ^[116,132]. Failure prediction architecture for safety-critical CPS has been proposed in ^[133]. Distinctive features of the architecture involve online operation, no usage of components specific as well internal logic application related data. The presented approach requires only the network traffic analysis based on system behavior.

Importantly, safety verification in safety-critical CPS can help to reduce risks, costs and time-to-market ^{[134,135,136,137]}. The presented work attempts to create a framework for safety verification and validation which will allow collaborative approach through combined efforts of specialists from different system design domains including software, hardware, etc. This can provide extended view of all system levels in the context of safety assurance. Formal verification process for safety critical Cyber Physical systems with application in automotive domain was proposed in ^[138]. The approach was aimed at safety analysis of system models with respect to safety relevant attributes. Issues of functional safety were raised in ^[139] and accordingly approach for safety risks analysis was proposed. The work presented in ^[140,141] represents a survey on validation and verification approaches aimed at giving an overview of existing gaps and current trends, including safety and security issues in cyber physical systems. Importantly, the work highlights the fact that there still is a gap between formal modeling of computational processes and modeling of physical processes.

Collaborative approaches to ensure the safety of a system has gained much attention. In this context, the idea presented in ^{[142,143,144]} is based on safety messages shared by cooperative vehicle safety systems. The system under consideration sends two types of messages over certain period of time: which includes event driven messages of high priority, and regular vehicle tracking messages to communicate with other vehicles in the vicinity. Thus the vehicles create a network of collaborative entities which allows self-improvement as well as environment awareness. The concept of reactive controllers and control-based protocols is widely employed in context of CPS. Reactive controllers are the entities which check the consistency of the systems behavior to a predefined requirements and act in proactive manner by collaborating with corresponding physical environment. These requirements, called contracts' are represented through linear temporal and signal temporal logic. Collaborative efforts for improving the overall CPS safety are very important, as CPS cover a wide range of domains, including human-system interaction, physical components, cyber components, communication elements, etc. Thus it is very important to understand and consider the interrelations among these heterogeneous, distributed elements ^[145,146].

6.   Open research issues

This section is devoted to discussion of some important open research issues in the context of security provision of CPS.

Enabling Collaborative Mechanisms for CPS Protection: Collaborative mechanisms apply to a common strategy of threats mitigation, but also to information exchange about already faced threats. The report released by McAfee ^[147] states that fragmented security approach is not effective anymore against modern threats. Furthermore, idea of an open integrated ecosystem for coordination of security activities was coined. Thus, security systems even belonging to different stakeholders will benefit from the knowledge exchange about faced threats. In this way, as the new threats appear even faster than threats mitigation solutions to cope with the threats, this will allow to reduce response time and resources needed. Another possible solution is shared knowledgebase, which is being improved by several parties and increase efficiency of threats mitigation.

Safety Communication for Geographically distributed points: As some of the key nodes or subsystems of a system can be geographically distributed, it makes the process of safer communication a critical challenge. Furthermore, applications accessing the data acquired by, for example the sensor nodes might be compromised and thus the sensor network is attacked in a passive way and these types of threats are hard to be detected. One possible solution could be extracted from the idea of federated learning, where data is not transmitted to the central node for processing, but being processed locally. Thus there is no need to send the local data set to a central server, but just an update to a global model ^[55].

Protection of critical infrastructure: Good example of critical infrastructure are the smart grids, which, according to ^[148], some key challenges are (ⅰ) heterogeneity of technologies and protocols, (ⅱ) weaknesses in communication protocols, as some of them don't posses mechanisms for security ensuring, (ⅲ) limited capabilities of some physical devices, (ⅳ) diversity of security strategies varying from one application domain to another.

Protection of Cyber and Physical components: Integrity is one of the major requirements of CPS. Attention needs to be paid to security aspects of a sensor network as well as to superstructures and data integrity. Another important issue applies to the lack of general methodology in developing secure CPS, thus there are many proprietary solutions, which may be based on potentially vulnerable approaches.

Security and Mobility: Mobile devices are potential carriers of threats, as they are contacting a lot of external networks and services. With the spread of wearable smart mobile assistants and implants, critical challenge lies in improving security measures for these devices, as they may harm the human health and even life.

Pro-active Security Systems: Based on previous threats, Pro-active systems enforced by analytical tools can suggest the main attack vectors and threats types. For instance, the most faced threat by a system could be DDoS attack, which requires special measures for exactly this type of threats. Thus, support tools for testing of system weaknesses and identifying the security priorities could ease the process of security policy improvement.

Integration and Analytic Tools: There is a clear need for new security models combining machine learning, decision making algorithms and human-assisted analysis. Human-assisted analysis is still an important factor in identifying previously faced threats. Furthermore, as the most faced threats need counter measures to be performed in real-time and since data volumes are extremely high, new solutions for reduced response time are needed.

7.   Conclusion

Cyber-Physical Systems are complex systems based on convergence of physical or hardware and cyber or software components. CPS has large variety of application areas: among others are transport, healthcare, wearables, home automation etc. The number of deployed CPS steadily increase, which causes several challenges related to security and safety. Some important elements and challenges of CPS were identified and discussed in this paper. Among which were the issues related to infrastructure as a key element of CPS with focus on networking. The role of virtualisation and its main types: network, resources and application were presented. Furthermore, in regard to evolving nature of the modern CPS and growing number of mobile components mobility aspects were also raised. Importance of new complex approaches in the area of Security and Privacy for CPS considering the influence of single components and subsystems threats on the whole system is discussed. Some salient threats and countermeasures including complex Intrusion Detection Systems with utilization of Machine Learning Algorithms were reviewed and debated. In addition threats modeling, which is very important on design stage to develop security mechanisms as well as to evaluate possible damage to the systems under different circumstances, has also been in the scope of this work. Necessity of joint security and safety consideration in order to identify the most complete set of potential threats is also highlighted in the paper. The first part of the paper is covering large variety of topics, which are relevant to understand the security and safety risks, subsequently the second part aims at giving the comprehensive overview of threats, attack vectors and mitigation approaches. In our future work we plan to analyze different threats and mitigation models considering the application domains with respect to heterogeneous and distributed nature of CPS and based on this introduce an appropriate set of measures for detecting and mitigating the security and safety risks domain specific.

Conflict of interest

The authors declare that there is no conflict of interest.