On the impact of quantum biology and relativistic time dilation in autism

Marco Ruggiero; Stefania Pacini; Marco Ruggiero; Stefania Pacini

doi:10.3934/molsci.2018.1.90

AIMS Molecular Science

2018, Volume 5, Issue 1: 90-95. doi: 10.3934/molsci.2018.1.90

Previous Article Next Article

Editorial

On the impact of quantum biology and relativistic time dilation in autism

Marco Ruggiero ^,,
Stefania Pacini

Silver Spring Sagl, Via Raimondo Rossi 24, Arzo-Mendrisio 6864, Switzerland

Received: 04 December 2017 Accepted: 21 March 2018 Published: 23 March 2018

This Editorial elaborates on innovative concepts presented at the 2^nd European Conference of Biomedical Research and Treatments for autism held in Bari, Italy, in November 2017. We discuss the recent publication of a paper describing how relativistic time dilation at the DNA level can lead to novel approaches in disease prevention and cure, and we elaborate on the role of the human microbiota in restoring quantum entanglement at the DNA level. According to this hypothesis, microbial degradation of a glycosaminoglycan, chondroitin sulfate, leads to restauration of gene expression, induces general and sequence-specific relativistic time dilation, restores DNA quantum entanglement, and improves the ability of DNA to retain, process and transmit information both at the biochemical and the quantum levels. It can be argued that these processes played a role in the evolution of the human brain and consciousness. Fermented aliments that today would be defined as “probiotics” were the first processed foods eaten by early humans, and it is conceivable that the effects of the microbes in those aliments on the chondroitin sulfate, coming from cartilage of animals hunted or scavenged, may have led to the biochemical, relativistic and quantum effects responsible for human evolution. Finally, we discuss the implications in the field of autism where the theory of consciousness based on quantum biology presents exciting and innovative perspectives for prevention and cure.

Keywords:

autism,
consciousness,
DNA

Citation: Marco Ruggiero, Stefania Pacini. On the impact of quantum biology and relativistic time dilation in autism[J]. AIMS Molecular Science, 2018, 5(1): 90-95. doi: 10.3934/molsci.2018.1.90

Related Papers:

[1]	Dewang Li, Meilan Qiu, Jianming Jiang, Shuiping Yang . The application of an optimized fractional order accumulated grey model with variable parameters in the total energy consumption of Jiangsu Province and the consumption level of Chinese residents. Electronic Research Archive, 2022, 30(3): 798-812. doi: 10.3934/era.2022042
[2]	María Guadalupe Morales, Zuzana Došlá, Francisco J. Mendoza . Riemann-Liouville derivative over the space of integrable distributions. Electronic Research Archive, 2020, 28(2): 567-587. doi: 10.3934/era.2020030
[3]	Li Tian, Ziqiang Wang, Junying Cao . A high-order numerical scheme for right Caputo fractional differential equations with uniform accuracy. Electronic Research Archive, 2022, 30(10): 3825-3854. doi: 10.3934/era.2022195
[4]	Ping Zhou, Hossein Jafari, Roghayeh M. Ganji, Sonali M. Narsale . Numerical study for a class of time fractional diffusion equations using operational matrices based on Hosoya polynomial. Electronic Research Archive, 2023, 31(8): 4530-4548. doi: 10.3934/era.2023231
[5]	Jin Li, Yongling Cheng . Barycentric rational interpolation method for solving time-dependent fractional convection-diffusion equation. Electronic Research Archive, 2023, 31(7): 4034-4056. doi: 10.3934/era.2023205
[6]	Xinguang Zhang, Yongsheng Jiang, Lishuang Li, Yonghong Wu, Benchawan Wiwatanapataphee . Multiple positive solutions for a singular tempered fractional equation with lower order tempered fractional derivative. Electronic Research Archive, 2024, 32(3): 1998-2015. doi: 10.3934/era.2024091
[7]	Ziqing Yang, Ruiping Niu, Miaomiao Chen, Hongen Jia, Shengli Li . Adaptive fractional physical information neural network based on PQI scheme for solving time-fractional partial differential equations. Electronic Research Archive, 2024, 32(4): 2699-2727. doi: 10.3934/era.2024122
[8]	Mehmet Ali Özarslan, Ceren Ustaoğlu . Extended incomplete Riemann-Liouville fractional integral operators and related special functions. Electronic Research Archive, 2022, 30(5): 1723-1747. doi: 10.3934/era.2022087
[9]	Yihui Xu, Benoumran Telli, Mohammed Said Souid, Sina Etemad, Jiafa Xu, Shahram Rezapour . Stability on a boundary problem with RL-Fractional derivative in the sense of Atangana-Baleanu of variable-order. Electronic Research Archive, 2024, 32(1): 134-159. doi: 10.3934/era.2024007
[10]	Jin Li, Yongling Cheng . Barycentric rational interpolation method for solving fractional cable equation. Electronic Research Archive, 2023, 31(6): 3649-3665. doi: 10.3934/era.2023185

Abstract

1. Introduction

Distributed-order fractional calculus (DOFC) is a branch of fractional calculus important for the modeling of complex systems. It generalizes the constant fractional operators by integrating the fractional kernel of these operators over an extended range of orders. The fractional differential operator of distributed order, for orders not great than 2, is given by

$\begin{align} & D^{\alpha} = \int_l^u b\left({\alpha} \right)\, \frac{d^\alpha}{dt^\alpha}\, d\alpha, \quad 0 \leq l < u \leq 2, \; \; b\left({\alpha} \right) \geq 0 \end{align}$ $

where $ \frac{d^\alpha}{dt^\alpha} $ stands for a single-order fractional derivative and $ b\left({\alpha} \right) $ is a non-negative weight function or generalized function. DOFC takes into account the superposition of orders and is a useful tool for modeling decelerating anomalous diffusion, ultraslow diffusive processes and strong anomaly (see e.g., ^[1,2]). DOFC models systems whose behavior stems from the complex interplay and superposition of nonlocal and memory effects occurring over a multitude of scales ^[3]. Over the last two decades, a significant number of papers appeared focusing on mathematical aspects and real-world applications of fractional partial differential equations with distributed order, see e.g., ^{[2,4,5,6,7,8,9,10,11,12,13,14,15]} for mathematical aspects, ^[16,17] for applications, and the review paper ^[18] about the mathematics of DOFC, including analytical, numerical methods, and the extensive overview of the recent applications of DOFC to fields like transport processes, and control theory. Moreover, DOFC was applied also in the study of composite materials ^[19,20] and viscoelastic materials having spatially varying properties ^[21].

The classical telegraph equation was first derived by Lord Kelvin in the 19th century ^[22]. It is a hyperbolic partial differential equation of the form

$\begin{align} c_2\, \partial_{tt}^2 u\left({x, t} \right) + \, c_1\, \partial_{t} u\left({x, t} \right) - c_0^2\, \partial_{xx}^2 u\left({x, t} \right) + d\, u\left({x, t} \right) = q\left({x, t} \right), \quad x \in \mathbb{R}, \; \; t > 0. \end{align}$ $

This equation was proposed by Cattaneo in 1958 (see ^[23]) to overcome the problem of infinite propagation velocity in heat transmission. Over the years, this equation and its time-fractional versions appeared in the study of several phenomena such as transmission lines for all frequencies ^[24], random walks ^[25], solar particle transport ^[26], oceanic diffusion ^[27], wave propagation ^[28], damped small vibrations, anomalous diffusion and wave-like processes ^{[29,30,31,32]}, scalar part of the Maxwell equations.

The TFTE with time-fractional derivatives of orders $ \alpha_1 \in]0, 1] $ and $ \alpha_2 \in]1, 2] $ was studied from the analytical, numerical, and probabilistic points of view by several authors. In ^[33], Cascaval et al. discussed the well-posedness of some initial-boundary value problems for the TFTE as well as the asymptotic behaviour of their solutions. In ^[31], the authors studied the neutral case of the TFTE and obtained an explicit Fourier representation of the fundamental solution (FS) and made a probabilistic interpretation of the FS in terms of stable probability density functions. Particular attention was given to the case $ \alpha_1 = 1/2 $ and $ \alpha_2 = 1 $ due to its connection of the telegraph process with Brownian motion. Some of these results were generalized by Camargo et al. in ^[34] for general $ \alpha_1 $ and $ \alpha_2 $ and studied later by Boyadjiev and Luchko in ^[29]. In ^[35], the authors considered a generalized telegraph equation with time-fractional derivatives in the Hilfer and Hadamard senses and space-fractional derivatives are in the sense of Riesz-Feller. Górska et al., (see ^[36]) considered various types of generalized telegraph equations and determine the conditions under which solutions can be recognized as probability density distributions.

The works ^{[32,37,38,39,40,41]} are examples of works devoted to the study of the TFTE in the multidimensional case with $ n $ space variables, where in some cases the second derivative in space is replaced by the Euclidean Laplace operator. In ^[32] the authors solved the multi-dimensional TFTE with multi-term time-fractional derivatives and proved that its fundamental solution is the law of a stable isotropic multi-dimensional process time-changed. Ovidio et al., ^[41] constructed compositions of vector processes whose distribution is related to space-time fractional $ n $-dimensional telegraph equations. We refer also the works of Masoliver and his co-workers about the TFTE and its connections with random walks (see ^{[42,43,44,45]}), and the recent survey paper ^[30] where is presented a very complete review of the fractional telegraph process. In ^[38,40] were employed Fourier, Laplace and Mellin transform techniques to obtain the first and second FS. Moreover, the application of the Residue Theorem allows obtaining double series representation for the FS of the TFTE in higher dimensions. Connections of the TFTE with fractional Clifford analysis and Sturm-Liouville theory were presented in ^[39] and ^[37].

In our recent paper ^[46] we studied the time-fractional telegraph equation with generalized distributed order in $ \mathbb{R}^n \times \mathbb{R}^+ $ finding a representation of the fundamental solution in terms of convolutions involving Fox H-functions. In this work, we extend our analysis to time-fractional telegraph equations of distributed order with Hilfer (or composite) time-fractional derivatives. Hilfer's derivative $ _{t}D_{0^+}^{\gamma, \nu} $ was defined by Hilfer as a two-parameter family of fractional derivatives of order $ \gamma > 0 $ and type $ \nu \in [0, 1] $ given by

$\begin{align} &\left({_{t}D_{0^+}^{\gamma, \nu} f} \right)\left({t} \right) \, = \left({I_{0^+}^{\nu\left({m-\gamma} \right)} \frac{d}{dt} \left({I_{0^+}^{(1-\nu) (m-\gamma)}f} \right)} \right)\left({t} \right), \end{align}$ $

where $ I_{0^+}^\gamma $ denotes the left Riemann-Liouville fractional integral of order $ \gamma > 0 $ (see Eq (2.1) in Section 2). The Hilfer fractional derivative allows to interpolate smoothly between the Riemann-Liouville and the Caputo fractional derivatives (see ^[16,47,48]). These special cases are obtained when $ \nu = 0 $ and $ \nu = 1, $ respectively. The type-parameter produces more stationary states, provides an extra degree of freedom on the initial condition, and increases the flexibility for the description of complex data. It was first used by Hilfer to describe the dynamics in glass formers over an extremely large-frequency window ^[49]. During the last years fractional differential equations with composite derivatives were studied by several authors, see e.g., ^{[35,50,51,52,53,54,55,56]}. In these works the equations are considered in $ \mathbb{R} \times \mathbb{R}^+ $, i.e., one single space variable and one time variable. Here, we consider the telegraph equation of distributed order with Hilfer time-fractional derivatives in the higher dimensional case, i.e., $ \mathbb{R}^n \times \mathbb{R}^+. $

The paper is organized as follows. In Section 2 we recall some basic facts about fractional derivatives, integral transforms, and special functions, which are necessary for the development of this work. In Section 3 we formulate the problem of generalized distributed order telegraph equation for general density functions. Following the ideas presented in ^[46], we use a combination of Laplace, Fourier and Mellin transforms to obtain a representation of the solution of our equation via convolution integrals involving Fox H-functions. The key points to obtain our main result are the use of the classical Titchmarsh's Theorem to invert the Laplace transform, and the use of the Mellin transform to invert the Fourier transform. Some particular cases of our equation are analyzed by considering specific choices of the parameters of the equation. In Section 4 we compute the expression of the fractional moments of arbitrary order of the first fundamental solution in the Laplace domain. For the particular case of single-order derivatives, we invert the Laplace transform of the second-order moment obtaining an expression in terms of the three-parameter Mittag-Leffler function. For numerical purposes, we study the corresponding asymptotic behavior of the second-order moment in the time domain for the long and short time limit, by using the Tauberian Theorem. In the final part of the paper, we present and analyze some plots of the second-order moment for this particular case. As it will be shown the graphical representations support the analytical conclusions obtained via the Tauberian Theorem.

2. Preliminaries

Let $ a, b \in \mathbb{R} $ with $ a < b $ and $ \alpha > 0 $. The left Riemann-Liouville fractional integral $ I_{a^+}^\gamma $ of order $ \gamma > 0 $ is given by (see ^[57])

$\begin{align} &\left({I_{a^+}^\gamma f} \right)\left({x} \right) \, = \frac{1}{\Gamma\left({\gamma} \right)} \int_a^x \frac{f\left({w} \right)}{\left({x-w} \right)^{1-\gamma}} \; dw, \qquad x > a. \end{align}$ $

The left Hilfer (or composite) fractional derivative $ _{t}D_{0^+}^{\gamma, \nu} $ of order $ \gamma > 0 $ and type $ 0 \leq \nu \leq 1 $ is given by (see ^[16,47,48])

(2.1)

where $ m = [\gamma]+1 $ and $ [\gamma] $ means the integer part of $ \gamma $. We observe that in the case when $ \nu = 0 $ we recover the left Riemann-Liouville fractional derivative and in the case when $ \nu = 1 $ we have the left Caputo fractional derivative. The previous definitions of fractional integrals and derivatives can be naturally extended to $ \mathbb{R}^n $ considering partial fractional integrals and derivatives (see Chapter 5 in ^[58]).

In this work, some integral transforms are used, namely, the Laplace, the Fourier and the Mellin transforms. The Laplace transform of a real-valued function $ f\left({t} \right) $ is defined by (see ^[57])

$\begin{align} & \mathcal{L}\left\{{f\left({t} \right)}\right\}\left({ \mathbf{s}}\right) \, = \widetilde{f}\left({ \mathbf{s}} \right) \, = \int_{0}^{+\infty} e^{- \mathbf{s} t} \, f\left({t} \right) \, dt, \quad \mathrm{Re}\left({ \mathbf{s}} \right) \in \mathbb{C} \end{align}$ $

and when it is applied to Eq (2.1) leads to (see ^[50])

$\begin{align} & \mathcal{L}\left\{{_{t}D_{0^+}^{\gamma, \nu} f\left({t} \right)}\right\}\left({ \mathbf{s}}\right) \, = \mathbf{s}^\gamma \, \widetilde{f}\left({ \mathbf{s}} \right) -\sum\limits_{j = 0}^{m-1} \mathbf{s}^{m-j-\nu\left({m-\gamma} \right)-1} \left[{\frac{d^j}{dt^j} \left({{}_{t}I_{0^+}^{\left({1-\nu} \right)\left({m-\gamma} \right)}f} \right)} \right]\left({0^+} \right), \end{align}$ $

(2.2)

where the initial-value terms $ \left[{\frac{d^k}{dt^k} \left({{}_{t}I_{0^+}^{\left({1-\nu} \right)\left({m-\gamma} \right)}f} \right)} \right]\left({0^+} \right) $ are evaluated in the limit $ t \to 0^+ $. Concerning the inverse Laplace transform of functions involving a branch point, we have the following theorem from Titchmarsh (see ^[59]).

Theorem 2.1. Let $ \widetilde{f}\left({ \mathbf{s}} \right) $ be an analytic function which has a branch cut on the real negative semiaxis, which has the following properties

$\begin{align} & \widetilde{f}\left({ \mathbf{s}} \right) \, = O\left({1} \right), \quad \left|{ \mathbf{s}}\right| \to +\infty, \qquad \qquad \widetilde{f}\left({ \mathbf{s}} \right) = O\left({\frac{1}{\left|{ \mathbf{s}}\right|}} \right), \quad \left|{ \mathbf{s}}\right| \to 0, \end{align}$ $

for any sector $ \left|{\arg\left({ \mathbf{s}} \right)}\right| < \pi-\eta $, where $ 0 < \eta < \pi $. Then the inverse Laplace transform of $ \widetilde{f}\left({ \mathbf{s}} \right) $ is given by

$\begin{align} f\left({t} \right) \, = \mathcal{L}^{-1}\left\{{\widetilde{f}\left({ \mathbf{s}} \right)}\right\}\left({t}\right) \, = - \frac{1}{\pi} \, \int_{0}^{+\infty} e^{-rt} \, \mathrm{Im}\left({\widetilde{f}\left({r e^{i\pi}} \right)} \right) \, dr, \end{align}$ $

where $ \mathrm{Im}\left({\cdot} \right) $ denotes the imaginary part.

The convolution of two integrable functions $ f $ and $ g $ with support in $ [0, +\infty) $ is defined by

$\begin{align} \left({f \ast_{{t}} g} \right)\left({t} \right) \, = \int_{0}^{t} f\left({t-w} \right) \, g\left({w} \right) \, dw, \qquad t \in \mathbb{R}^+ \end{align}$ $

(2.3)

and the Convolution Theorem for the Laplace transform is given by

$\begin{align} \mathcal{L}\left\{{\left({f \ast_{{t}} g} \right)\left({t} \right)}\right\}\left({ \mathbf{s}}\right) \, = \mathcal{L}\left\{{f}\right\}\left({ \mathbf{s}}\right) \, \mathcal{L}\left\{{g}\right\}\left({ \mathbf{s}}\right). \end{align}$ $

(2.4)

The $ n $-dimensional Fourier transform of a real-valued integrable function $ f $ in $ \mathbb{R}^n $ is defined by (see ^[57])

$\begin{align} & \mathcal{F}\left\{{f\left({x} \right)}\right\}\left({\kappa}\right) \, = \widehat{f}\left({\kappa} \right) \, = \int_{ \mathbb{R}^n} e^{i\kappa \cdot x} \, f\left({x} \right) \, dx, \qquad \kappa \in \mathbb{R}^n, \end{align}$ $

while the corresponding inverse Fourier transform is given formally by

$\begin{align} & f\left({x} \right) \, = \mathcal{F}^{-1}\left\{{\widehat{f}\left({\kappa} \right)}\right\}\left({x}\right) \, = \frac{1}{\left({2\pi} \right)^n} \int_{ \mathbb{R}^n} e^{-ix \cdot \kappa} \, \widehat{f}\left({\kappa} \right) \, d\kappa, \qquad x \in \mathbb{R}^n. \end{align}$ $

(2.5)

The convolution operator of two functions in $ \mathbb{R}^n $ is defined by the integral

$\begin{align} \left({f \ast_{{x}} g} \right)\left({x} \right) \, = \int_{ \mathbb{R}^n} f\left({x-z} \right) \, g\left({z} \right) \, dz, \qquad x \in \mathbb{R}^n \end{align}$ $

(2.6)

and the Convolution Theorem for the Fourier transform is given by

$\begin{align} \mathcal{F}\left\{{\left({f \ast_{{x}} g} \right)\left({x} \right)}\right\}\left({\kappa}\right) \, = \mathcal{F}\left\{{f}\right\}\left({\kappa}\right) \, \mathcal{F}\left\{{g}\right\}\left({\kappa}\right). \end{align}$ $

(2.7)

For the $ n $-dimensional Laplace operator $ \Delta_x = \sum_{i = 1}^{n} \frac{\partial^2}{\partial x_i^2} $ we have (see formula (1.3.32) in ^[57])

$\begin{align} \mathcal{F}\left\{{\Delta_x f\left({x} \right)}\right\}\left({\kappa}\right) \, = -|\kappa|^2 \, \mathcal{F}\left\{{f\left({x} \right)}\right\}\left({\kappa}\right). \end{align}$ $

(2.8)

Another integral transform that we use in this work is the Mellin transform. For $ f $ locally integrable on $]0, +\infty[$ it is defined by (see ^[57])

$\begin{align} & \mathcal{M}\left\{{f\left({w} \right)}\right\}\left({s}\right) \, = f^\ast\left({s} \right) \, = \int_{0}^{+\infty} w^{s -1} \, f\left({w} \right) \, dw, \qquad s \in \mathbb{C}, \end{align}$ $

(2.9)

and the inverse Mellin transform is given by

$\begin{align} & f\left({w} \right) \, = \mathcal{M}^{-1}\left\{{f^\ast\left({s} \right)}\right\}\left({w}\right) \, = \frac{1}{2\pi i} \, \int_{\gamma-i\infty}^{\gamma+i\infty} w^{-s} \, f\left({s} \right) \, ds, \qquad w > 0, \quad \gamma = \mathrm{Re}\left({s} \right). \end{align}$ $

(2.10)

The condition for the existence of Eq (2.9) is that $ -p < \gamma < -q $ (called the fundamental strip), where $ p $, $ q $ are the order of $ f $ at the origin and $ \infty $, respectively. The integration in Eq (2.10) is performed along the imaginary axis and the result does not depend on the choice of $ \gamma $ inside the fundamental strip. For more information about this transform and its properties, see e.g., ^[57]. The Mellin convolution between two functions is defined by

$\begin{align} &\left({f \ast_{\mathcal{M}} g} \right)\left({x} \right) \, = \int_{0}^{+\infty} f\left({\frac{x}{u}} \right) \; g\left({u} \right) \; \frac{du}{u}, \end{align}$ $

(2.11)

and satisfies the Mellin Convolution Theorem (see formula (1.4.40) in ^[57])

$\begin{align} & \mathcal{M}\left\{{f \ast_{\mathcal{M}} g}\right\}\left({s}\right) = \mathcal{M}\left\{{f}\right\}\left({s}\right) \; \mathcal{M}\left\{{g}\right\}\left({s}\right). \end{align}$ $

The following relation holds (see (1.4.30) in ^[57])

$\begin{align} & \mathcal{M}\left\{{f\left({\frac{1}{x}} \right)}\right\}\left({s}\right) \, = \mathcal{M}\left\{{f}\right\}\left({-s}\right). \end{align}$ $

(2.12)

The solution of the time-fractional telegraph equation of distributed order obtained in this work involves the Fox H-function $ H_{p, q}^{m, n} $, which is defined, via a Mellin-Barnes type integral, by (see ^[60])

$\begin{eqnarray} \!\!\!\!\! H_{{p, q}}^{{m, n}} \left[\begin{array}{c|c} \begin{array}{c} \!\!\! {z} \!\! \end{array} & \begin{array}{c} \!\! {\left({a_1, \; \alpha_1} \right), \ldots, \left({a_p, \; \alpha_p} \right)} \!\!\! \\[0.5 cm] \!\! {\left({b_1, \; \beta_1} \right), \ldots, \left({b_q, \; \beta_q} \right)} \!\!\! \end{array} \end{array}\right] \, = \frac{1}{2\pi i} \int_{\mathcal{C}} \frac{ \prod\nolimits_{j = 1}^{m} \Gamma\left({b_j+\beta_j s} \right) \; \prod\nolimits_{i = 1}^{n} \Gamma\left({1-a_i-\alpha_i s} \right)}{ \prod\nolimits_{i = n+1}^{p} \Gamma\left({a_i+\alpha_i s} \right) \; \prod\nolimits_{j = m+1}^{q} \Gamma\left({1-b_j-\beta_j s} \right)} \; z^{-s} \; ds, \end{eqnarray}$ $

(2.13)

where $ a_i, b_j \in \mathbb{C}, $ and $ \alpha_i, \beta_j \in \mathbb{R}^+, $ for $ i = 1, \ldots, p $ and $ j = 1, \ldots, q $ and $ \mathcal{C} $ is a suitable contour in the complex plane separating the poles of the two factors in the numerator (see ^[60]). The expression of the second-order moment in Section 4.1 is presented in terms of the three parameter Mittag-Leffler function $ E_{{\beta_1}, {\beta_2}}^{{\beta_3}}(z) $ (see ^[61]), which is defined, in terms of power series, by

$\begin{align} & E_{{\alpha}, {\beta}}^{{\gamma}}(z) = \sum\limits_{k = 0}^\infty \frac{\left({\gamma} \right)_k z^k}{k! \, \Gamma\left({\alpha k +\beta} \right)}, \quad z \in \mathbb{C}, \; \; \alpha, \beta, \gamma \in \mathbb{R}, \; \; \alpha > 0, \end{align}$ $

(2.14)

where $ \left({\gamma} \right)_k $ is the Pochhammer symbol.

Throughout the paper, we assume that all the involved functions are Laplace and Fourier transformable.

3. Generalized time-fractional telegraph equation of distributed order

In this work we consider the following generalized time-fractional telegraph equation of distributed order

$\begin{align} & \int_{0}^{1} \int_{1}^{2} b_2\left({\beta, \nu} \right) \, {}_{{t}}\partial_{{0^+}}^{{\beta}, {\nu}} u\left({x, t} \right) \, d\beta \, d\nu\ +a \, \int_{0}^{1} \int_{0}^{1} b_1\left({\alpha, \mu} \right) \, {}_{{t}}\partial_{{0^+}}^{{\alpha}, {\mu}} u\left({x, t} \right) \, d\alpha \, d\mu \\[0.2cm] & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad -c^2 \, \Delta_x u\left({x, t} \right) +d^2 \, u\left({x, t} \right) \, = q\left({x, t} \right), \end{align}$ $

(3.1)

for given weight functions $ b_2\left({\beta, \nu} \right) > 0 $ and $ b_1\left({\alpha, \mu} \right) > 0 $, satisfying

$\begin{equation} \int_{0}^{1}\int_{1}^{2} b_2\left({\beta, \nu} \right) \, d\beta \, d\nu = C_2, \qquad \int_{0}^{1}\int_{0}^{1} b_1\left({\alpha, \mu} \right) \, d\alpha \, d\mu = C_1, \end{equation}$ $

(3.2)

and subject to the following initial and boundary conditions

$\begin{align} & \left({{}_{{t}}I_{{0^+}}^{{\left({1-\mu} \right)\left({1-\alpha} \right)}}u} \right)\left({x, 0^+} \right) = f\left({x} \right), \qquad \left({{}_{{t}}I_{{0^+}}^{{\left({1-\nu} \right)\left({2-\beta} \right)}}u} \right)\left({x, 0^+} \right) = g_1\left({x} \right) \end{align}$ $

(3.3)

$\begin{align} [0.2cm] & \left[{\frac{\partial}{\partial t}\left({{}_{{t}}I_{{0^+}}^{{\left({1-\nu} \right)\left({2-\beta} \right)}}u} \right)} \right]\left({x, 0^+} \right) = g_2\left({x} \right), \qquad \lim\limits_{|x|\to +\infty} u\left({x, t} \right) = 0, \end{align}$ $

(3.4)

where $ \left({x, \, t} \right) \in \mathbb{R}^n \times \mathbb{R}^+ $, $ \Delta_x $ is the classical Laplace operator in $ \mathbb{R}^n $, the partial time-fractional derivatives of order $ \beta \in \, ]1, 2] $ and $ \alpha \in \, ]0, 1] $, and types $ \mu, \nu \in [0, 1] $ are in the Hilfer sense and given by Eq (2.1), $ a \in \mathbb{R}_0^+ $, $ c \in \mathbb{R} \setminus\{0\} $, $ d \in \mathbb{R} $, and $ C_1, C_2 \in \mathbb{R}^+ $. The positive constants $ C_1 $ and $ C_2 $ can be taken as 1 if we assume the normalization condition for the integrals Eq (3.2). Moreover, $ q $ belongs to $ L_1\left({ \mathbb{R}^n \times I} \right) $, and $ f, g_1, g_2 \in L_1\left({ \mathbb{R}^n} \right) $. We look for solutions $ u\left({x, t} \right) $ of our problem in the space $ C^2\left({ \mathbb{R}^n} \right) \times C^2\left({0, +\infty} \right) $ with possible exception at $ x = 0 $.

3.1. Solution in the Fourier-Laplace domain

In order to analytically determine the solution of Eqs (3.1) and (3.2) in the space-time domain we start applying the Fourier and Laplace transforms to Eq (3.1) and solve the equation in the Fourier-Laplace domain. After that, there are two alternative strategies related to the order in carrying out the inversions of the Fourier and Laplace transforms are performed (see ^[2]):

$ \rm(S1) $ invert the Fourier transform, yielding $ \widetilde{u}\left({x, s} \right) $, and then invert the Laplace transform of the result.

$ \rm(S2) $ invert the Laplace transform, yielding $ \widehat{u}\left({\kappa, t} \right) $, and then invert the Fourier transform of the result.

In this work, we consider the strategy (S2) where the inversion of the Laplace transform is performed via the classical Titchmarsh's Theorem, and the inversion of the Fourier transform is performed via the Mellin transform.

we start by applying in Eq (3.1) the Laplace transform with respect to the variable $ t \in \mathbb{R}^+ $ and the $ n $-dimensional Fourier transform with respect to the variable $ x \in \mathbb{R}^n $. Taking into account relations Eq (2.2) and Eq (2.8), and the initial conditions in Eqs (3.3) and (3.4), we obtain

$\begin{align} & \widehat{\widetilde{u}}\left({\kappa, \mathbf{s}} \right) \, \int_{0}^{1} \int_{1}^{2} b_2\left({\beta, \nu} \right) \, \mathbf{s}^\beta \, d\beta \, d\nu -\widehat{g}_1\left({\kappa} \right) \, \int_{0}^{1}\int_{1}^{2} b_2\left({\beta, \nu} \right) \, \mathbf{s}^{1-\nu\left({2-\beta} \right)} \, d\beta \, d\nu \\[0.2cm] & \qquad -\widehat{g}_2\left({\kappa} \right) \, \int_{0}^{1}\int_{1}^{2} b_2\left({\beta, \nu} \right) \, \mathbf{s}^{-\nu\left({2-\beta} \right)} \, d\beta \, d\nu +a \, \widehat{\widetilde{u}}\left({\kappa, \mathbf{s}} \right) \int_{0}^{1}\int_{0}^{1} b_1\left({\alpha, \mu} \right) \, \mathbf{s}^{\alpha} \, d\alpha \, d\mu \\[0.2cm] & \qquad -a \, \widehat{f}\left({\kappa} \right) \int_{0}^{1} \int_{0}^{1} b_1\left({\alpha, \mu} \right) \, \mathbf{s}^{-\mu\left({1-\alpha} \right)} \, d\alpha \, d\mu +c^2 \, \left|{\kappa}\right|^2 \, \widehat{\widetilde{u}}\left({\kappa, \mathbf{s}} \right) +d^2 \, \widehat{\widetilde{u}}\left({\kappa, \mathbf{s}} \right) = \widehat{\widetilde{q}}\left({\kappa, \mathbf{s}} \right), \end{align}$ $

which is equivalent to

$\begin{align} \widehat{\widetilde{u}}\left({\kappa, \mathbf{s}} \right) & = \frac{\widehat{f}\left({\kappa} \right) \, B_1^\ast\left({ \mathbf{s}} \right)}{B_2\left({ \mathbf{s}} \right) +B_1\left({ \mathbf{s}} \right)+|\kappa|^2} +\frac{\widehat{g}_1\left({\kappa} \right) \, \left({B_2^\ast\left({ \mathbf{s}} \right)-\frac{d^2}{c^2}} \right)}{ \mathbf{s}^{-1} \, \left({B_2\left({ \mathbf{s}} \right) +B_1\left({ \mathbf{s}} \right)+|\kappa|^2} \right)} \\[0.2cm] & \qquad +\frac{\widehat{g}_2\left({\kappa} \right) \, \left({B_2^\ast\left({ \mathbf{s}} \right)-\frac{d^2}{c^2}} \right)}{B_2\left({ \mathbf{s}} \right) +B_1\left({ \mathbf{s}} \right)+|\kappa|^2} +\frac{\widehat{\widetilde{q}}\left({\kappa, \mathbf{s}} \right)}{c^2 \, \left({B_2\left({ \mathbf{s}} \right)+B_1\left({ \mathbf{s}} \right)+|\kappa|^2} \right)}, \end{align}$ $

(3.5)

where $ \widehat{f} $ and $ \widehat{g}_i $ are the Fourier transforms of the functions $ f $ and $ g_i $, respectively, and

$\begin{align} & B_2\left({ \mathbf{s}} \right) \, = \frac{1}{c^2} \, \left({\int_{0}^{1}\int_{1}^{2} b_2\left({\beta, \nu} \right) \, \mathbf{s}^\beta \, d\beta \, d\nu +d^2} \right), & B_1\left({ \mathbf{s}} \right) \, = \frac{a}{c^2} \, \int_{0}^{1}\int_{0}^{1} b_1\left({\alpha, \mu} \right) \, \mathbf{s}^\alpha \, d\alpha \, d\mu, \end{align}$ $

(3.6)

$\begin{align} & B_2^\ast\left({ \mathbf{s}} \right) \, = \frac{1}{c^2} \, \left({\int_{0}^{1}\int_{1}^{2} b_2\left({\beta, \nu} \right) \, \mathbf{s}^{-\nu\left({2-\beta} \right)} \, d\beta \, d\nu +d^2} \right), & B_1^\ast\left({ \mathbf{s}} \right) \, = \frac{a}{c^2} \, \int_{0}^{1}\int_{0}^{1} b_1\left({\alpha, \mu} \right) \, \mathbf{s}^{-\mu\left({1-\alpha} \right)} \, d\alpha \, d\mu. \end{align}$ $

(3.7)

Remark 3.1. When $ \mu = \nu = 1 $, i.e., the telegraph equation has only Caputo fractional derivatives, we have the following relations between Eqs (3.6) and (3.7)

$\begin{align} B_1^\ast\left({ \mathbf{s}} \right) \, = \mathbf{s}^{-1} \, B_1\left({s} \right) \qquad \ { and } \ \qquad B_2^\ast\left({ \mathbf{s}} \right) -\frac{d^2}{c^2}\, = s^{-2} \left({B_2\left({ \mathbf{s}} \right)-\frac{d^2}{c^2}} \right). \end{align}$ $

The previous relations combined with the fact that Eqs (3.3) and (3.4) reduce to

$\begin{align} & u\left({x, 0} \right) = f\left({x} \right), \qquad u\left({x, 0} \right) = g_1\left({x} \right), \qquad \frac{\partial u}{\partial t}\left({x, 0} \right) = g_2\left({x} \right), \end{align}$ $

i.e., $ f = g_1 $ when $ \nu = \mu = 1 $, allow us to reduce the expression (3.5) to the correspondent one obtained in ^[46].

3.2. Solution in the space-time domain

In this section we perform the inversion of the Laplace and Fourier transforms in order to obtain our solution in the space-time domain. Let us consider the following auxiliary functions in the Laplace domain

$\begin{align} & \widehat{\widetilde{u}}_1\left({\kappa, \mathbf{s}} \right) \, = \frac{B_1^\ast\left({ \mathbf{s}} \right)}{ B_2\left({ \mathbf{s}} \right) +B_1\left({ \mathbf{s}} \right) +|\kappa|^2}, \end{align}$ $

(3.8)

$\begin{align} [0.2cm] & \widehat{\widetilde{u}}_2\left({\kappa, \mathbf{s}} \right) \, = \frac{B_2^\ast\left({ \mathbf{s}} \right)}{ \mathbf{s}^p \, \left({B_2\left({ \mathbf{s}} \right) +B_1\left({ \mathbf{s}} \right) +|\kappa|^2} \right)}, \end{align}$ $

(3.9)

$\begin{align} [0.2cm] & \widehat{\widetilde{u}}_3\left({\kappa, \mathbf{s}} \right) \, = \frac{1}{ \mathbf{s}^p \, \left({B_2\left({ \mathbf{s}} \right) +B_1\left({ \mathbf{s}} \right) +|\kappa|^2} \right)}, \end{align}$ $

(3.10)

with $ p = 0 $ or $ p = -1. $ To further proceed we make the following additional assumption:

$\begin{align} & \mbox{(H1): The functions } \widehat{\widetilde{u}}_j\left({\kappa, re^{i\pi}} \right), j = 1, 2, 3 \mbox{ are in the conditions of Theorem 2.1}. \end{align}$ $

(3.11)

Assumption (H1) holds for the particular cases we consider later on. Applying Theorem 2.1, we have

$\begin{align} & \widehat{u}_j\left({\kappa, t} \right) \, = -\frac{1}{\pi} \, \int_{0}^{+\infty} e^{-rt} \, \mathrm{Im}\left({ \widehat{\widetilde{u}}_j\left({\kappa, r e^{i\pi}} \right)} \right) \, dr, \quad j = 1, 2, 3. \end{align}$ $

(3.12)

To evaluate the imaginary parts of the functions $ \widehat{\widetilde{u}}_j\left({\kappa, re^{i\pi}} \right) $, $ j = 1, 2, 3 $, along the ray $ \mathbf{s} = re^{i\pi} $, with $ r > 0 $, we consider the following polar decompositions

$\begin{align} & B_l\left({re^{i\pi}} \right) \, = \rho_l \left({\cos\left({\gamma_l\pi} \right) +i \, \sin\left({\gamma_l \pi} \right)} \right) \, \Longrightarrow \begin{cases} \rho_l \, = \left|{B_l\left({re^{i\pi}} \right)}\right| \\[0.2cm] \gamma_l \, = \dfrac{1}{\pi} \, \arg\left({B_l\left({re^{i\pi}} \right)} \right)\end{cases}, \quad l = 1, 2 \end{align}$ $

(3.13)

$\begin{align} [0.2cm] & B_l^\ast\left({re^{i\pi}} \right) \, = \rho_l^\ast \left({\cos\left({\gamma_l^\ast \pi} \right) +i \, \sin\left({\gamma_l^\ast \pi} \right)} \right) \, \Longrightarrow \begin{cases} \rho_l^\ast \, = \left|{B_l^\ast\left({re^{i\pi}} \right)}\right| \\[0.2cm] \gamma_l^\ast \, = \dfrac{1}{\pi} \, \arg\left({B_l^\ast\left({re^{i\pi}} \right)} \right)\end{cases}, \quad l = 1, 2. \end{align}$ $

(3.14)

After straightforward calculations, we obtain the following expressions

$\begin{align} & \mathrm{Im} \left\{{\widehat{\widetilde{u}}_1 \left({\kappa, re^{i\pi}} \right)}\right\} \, = K_1\left({\left|{\kappa}\right|, r} \right) \, = \frac{\rho_1^\ast \left[{\left({A +\left|{\kappa}\right|^2} \right) \sin\left({\gamma_1^\ast \pi} \right) -B \, \cos\left({\gamma_1^\ast \pi} \right)} \right]}{ \, \left[{\left({A +\left|{\kappa}\right|^2} \right)^2 +B^2} \right]}, \end{align}$ $

(3.15)

$\begin{align} [0.2cm] & \mathrm{Im} \left\{{\widehat{\widetilde{u}}_2\left({\kappa, re^{i\pi}} \right)}\right\} \, = K_2\left({p, \left|{\kappa}\right|, r} \right) \, = \frac{\rho_2^\ast \left[{\left({A +\left|{\kappa}\right|^2} \right) \sin\left({\gamma_2^\ast \pi} \right) -B \, \cos\left({\gamma_2^\ast \pi} \right)} \right]}{\left({-r} \right)^p \, \left[{\left({A +\left|{\kappa}\right|^2} \right)^2 +B^2} \right]}, \end{align}$ $

(3.16)

$\begin{align} [0.2cm] & \mathrm{Im} \left\{{\widehat{\widetilde{u}}_3\left({\kappa, re^{i\pi}} \right)}\right\} \, = K_3\left({p, \left|{\kappa}\right|, r} \right) \, = \frac{-B}{\left({-r} \right)^p \, \left[{\left({A +\left|{\kappa}\right|^2} \right)^2 +B^2} \right]}, \end{align}$ $

(3.17)

where

$\begin{align} & A = \rho_2 \cos\left({\gamma_2\pi} \right) +\rho_1 \cos\left({\gamma_1\pi} \right) \qquad \text{ and } \qquad B = \rho_2 \sin\left({\gamma_2 \pi} \right) +\rho_1 \sin\left({\gamma_1 \pi} \right). \end{align}$ $

(3.18)

Remark 3.2. Taking into account Remark 3.1, when $ \mu = \nu = 1 $ we have, by straightforward calculations, the following relations

$\begin{align} \begin{cases} \rho_2^\ast \, = r^{-2} \, \rho_2 \\[0.2cm] \gamma_2^\ast \, = \gamma_2 \end{cases} \qquad \ and \ \qquad \begin{cases} \rho_1^\ast \, = r^{-1} \, \rho_1 \\[0.2cm] \gamma_1^\ast \, = 1+\gamma_1 \end{cases}. \end{align}$ $

Applying the inverse Laplace transform to Eq (3.5) and taking into account Eqs (3.12), (3.15), (3.16) and (3.17), we obtain

$\begin{align} \widehat{u}\left({\kappa, t} \right) & = -\frac{\widehat{f}\left({\kappa} \right)}{\pi} \, \int_{0}^{+\infty} e^{-rt} \, K_1\left({\left|{\kappa}\right|, r} \right) \, dr \\[0.2cm] & \quad -\frac{\widehat{g}_1\left({\kappa} \right)}{\pi} \, \int_{0}^{+\infty} e^{-rt} \, \left[{K_2\left({-1, \left|{\kappa}\right|, r} \right) -\frac{d^2}{c^2} \, K_3\left({-1, \left|{\kappa}\right|, r} \right)} \right] \, dr \\[0.2cm] & \quad -\frac{\widehat{g}_2\left({\kappa} \right)}{\pi} \, \int_{0}^{+\infty} e^{-rt} \, \left[{K_2\left({0, \left|{\kappa}\right|, r} \right) -\frac{d^2}{c^2} \, K_3\left({0, \left|{\kappa}\right|, r} \right)} \right] \, dr \\[0.2cm] & \quad -\frac{\widehat{q}\left({\kappa, t} \right)}{\pi c^2} \ast_{{t}} \int_{0}^{+\infty} e^{-rt} \, K_3\left({0, \left|{\kappa}\right|, r} \right) \, dr , \end{align}$ $

(3.19)

where $ \ast_{{t}} $ is given by Eq (2.3) and in the last term me made use of Eq (2.4). For the inversion of the Fourier transform, taking into account Eqs (2.5) and (2.7), we obtain

$\begin{align} u\left({x, t} \right) & = - f\left({x} \right) \ast_{{x}} \mathcal{F}^{-1}\left\{{\frac{1}{\pi} \, \int_{0}^{+\infty} e^{-rt} \, K_1\left({\left|{\kappa}\right|, r} \right) \, dr}\right\}\left({x, t}\right) \\[0.2cm] & \quad -g_1\left({x} \right) \ast_{{x}} \mathcal{F}^{-1}\left\{{\frac{1}{\pi} \, \int_{0}^{+\infty} e^{-rt} \, \left[{K_2\left({-1, \left|{\kappa}\right|, r} \right) -\frac{d^2}{c^2} \, K_3\left({-1, \left|{\kappa}\right|, r} \right)} \right] \, dr}\right\}\left({x, t}\right) \\[0.2cm] & \quad -g_2\left({x} \right) \ast_{{x}} \mathcal{F}^{-1}\left\{{\frac{1}{\pi} \, \int_{0}^{+\infty} e^{-rt} \, \left[{K_2\left({0, \left|{\kappa}\right|, r} \right) -\frac{d^2}{c^2} \, K_3\left({0, \left|{\kappa}\right|, r} \right)} \right] \, dr}\right\}\left({x, t}\right) \\[0.2cm] & \quad -q\left({x, t} \right) \ast_{{t}} \ast_{{x}} \, \mathcal{F}^{-1}\left\{{\frac{1}{\pi c^2} \, \int_{0}^{+\infty} e^{-rt} \, K_3\left({0, \left|{\kappa}\right|, r} \right) \, dr}\right\}\left({x}\right). \end{align}$ $

(3.20)

Using the following formula presented in ^[58] for the inverse Fourier transform of $ L_1 $-functions

$\begin{align} & \frac{1}{\left({2\pi} \right)^n} \int_{ \mathbb{R}^n} e^{-ix \cdot \kappa} \, \varphi\left({\left|{\kappa}\right|} \right) \, d\kappa \, = \frac{\left|{x}\right|^{1-\frac{n}{2}}}{\left({2\pi} \right)^{\frac{n}{2}}} \int_{0}^{+\infty} \varphi\left({w} \right) \, w^{\frac{n}{2}} \, J_{{\frac{n}{2}-1}}\left({\left|{x}\right|w}\right) \, dw, \end{align}$ $

(3.21)

and since we are dealing with radial functions in $ \kappa $, Eq (3.20) can be rewritten as

$\begin{align} & u\left({x, t} \right) \\[0.2cm] & = -\frac{1}{\pi} \, f\left({x} \right) \ast_{{x}} \left[{\frac{\left|{x}\right|^{1-\frac{n}{2}}}{\left({2\pi} \right)^{\frac{n}{2}}} \, \int_{0}^{+\infty} \, \int_{0}^{+\infty} e^{-rt} \, K_1\left({w, r} \right) \, dr \, w^{\frac{n}{2}} \, J_{{\frac{n}{2}-1}}\left({\left|{x}\right|w}\right) \, dw} \right] \\[0.2cm] & \quad-\frac{1}{\pi} \, g_1\left({x} \right) \ast_{{x}} \left[{\frac{\left|{x}\right|^{1-\frac{n}{2}}}{\left({2\pi} \right)^{\frac{n}{2}}} \, \int_{0}^{+\infty} \, \int_{0}^{+\infty} e^{-rt} \, \left[{K_2\left({-1, w, r} \right) -\frac{d^2}{c^2} \, K_3\left({-1, w, r} \right)} \right] \, dr \, w^{\frac{n}{2}} \, J_{{\frac{n}{2}-1}}\left({\left|{x}\right|w}\right) \, dw} \right] \\[0.2cm] & \quad-\frac{1}{\pi} \, g_2\left({x} \right) \ast_{{x}} \left[{\frac{\left|{x}\right|^{1-\frac{n}{2}}}{\left({2\pi} \right)^{\frac{n}{2}}} \, \int_{0}^{+\infty} \, \int_{0}^{+\infty} e^{-rt} \, \left[{K_2\left({0, w, r} \right) -\frac{d^2}{c^2} \, K_3\left({0, w, r} \right)} \right] \, dr \, w^{\frac{n}{2}} \, J_{{\frac{n}{2}-1}}\left({\left|{x}\right|w}\right) \, dw} \right] \\[0.2cm] & \quad-\frac{1}{\pi c^2} \, q\left({x, t} \right) \ast_{{t}} \ast_{{x}} \, \left[{\frac{\left|{x}\right|^{1-\frac{n}{2}}}{\left({2\pi} \right)^{\frac{n}{2}}} \, \int_{0}^{+\infty} \, \int_{0}^{+\infty} e^{-rt} \, K_3\left({0, w, r} \right) \, dr \, w^{\frac{n}{2}} \, J_{{\frac{n}{2}-1}}\left({\left|{x}\right|w}\right) \, dw} \right] \\[0.2cm] & = -\frac{1}{\pi} \, f\left({x} \right) \ast_{{x}} \Biggl[\int_{0}^{+\infty} e^{-rt} \, \underbrace{\frac{\left|{x}\right|^{1-\frac{n}{2}}}{\left({2\pi} \right)^{\frac{n}{2}}} \, \int_{0}^{+\infty} K_1\left({w, r} \right) \, w^{\frac{n}{2}} \, J_{{\frac{n}{2}-1}}\left({\left|{x}\right|w}\right) \, dw}_{\mathbf{I_1}} \, dr\Biggr] \\[0.2cm] & \quad -\frac{1}{\pi} \, g_1\left({x} \right) \ast_{{x}} \Biggl[\int_{0}^{+\infty} e^{-rt} \, \underbrace{\frac{\left|{x}\right|^{1-\frac{n}{2}}}{\left({2\pi} \right)^{\frac{n}{2}}} \, \int_{0}^{+\infty} \, \left[{K_2\left({-1, w, r} \right) -\frac{d^2}{c^2} \, K_3\left({-1, w, r} \right)} \right] \, w^{\frac{n}{2}} \, J_{{\frac{n}{2}-1}}\left({\left|{x}\right|w}\right) \, dw}_{\mathbf{I_2}} \, dr\Biggr] \\[0.2cm] & \quad -\frac{1}{\pi} \, g_2\left({x} \right) \ast_{{x}} \Biggl[\int_{0}^{+\infty} e^{-rt} \, \underbrace{\frac{\left|{x}\right|^{1-\frac{n}{2}}}{\left({2\pi} \right)^{\frac{n}{2}}} \, \int_{0}^{+\infty} \, \left[{K_2\left({0, w, r} \right) -\frac{d^2}{c^2} \, K_3\left({0, w, r} \right)} \right] \, w^{\frac{n}{2}} \, J_{{\frac{n}{2}-1}}\left({\left|{x}\right|w}\right) \, dw}_{\mathbf{I_3}} \, dr\Biggr] \\[0.2cm] & \quad -\frac{1}{\pi c^2} \, q\left({x, t} \right) \ast_{{t}} \ast_{{x}} \, \Biggl[\int_{0}^{+\infty} e^{-rt} \, \underbrace{\frac{\left|{x}\right|^{1-\frac{n}{2}}}{\left({2\pi} \right)^{\frac{n}{2}}} \, \int_{0}^{+\infty} \, K_3\left({0, w, r} \right) \, w^{\frac{n}{2}} \, J_{{\frac{n}{2}-1}}\left({\left|{x}\right|w}\right) \, dw}_{\mathbf{I_4}} \, dr\Biggr]. \end{align}$ $

(3.22)

To compute explicitly $ \mathbf{I_1} $, $ \mathbf{I_2} $, $ \mathbf{I_3} $, and $ \mathbf{I_4} $ in Eq (3.22) we are going to use the Mellin transform. First, we rewrite these integrals as a Mellin convolution Eq (2.11). In fact, considering the following auxiliary functions

$\begin{align} & g_1\left({w} \right) \, = K_1\left({w, r} \right), \qquad \qquad \qquad \qquad \qquad g_2\left({w} \right) \, = K_2\left({-1, w, r} \right) -\frac{d^2}{c^2} \, K_3\left({-1, w, r} \right), \\[0.2cm] & g_3\left({w} \right) \, = K_2\left({0, w, r} \right) -\frac{d^2}{c^2} \, K_3\left({0, w, r} \right), \qquad g_4\left({w} \right) \, = K_3\left({0, w, r} \right), \\[0.2cm] & f\left({w} \right) \, = \frac{1}{\left({2\pi} \right)^{\frac{n}{2}} \, \left|{x}\right|^n \, w^{\frac{n}{2}+1}} \, J_{{\frac{n}{2}-1}}\left({\frac{1}{w}}\right), \end{align}$ $

we have for $ i = 1, 2, 3, 4 $

$\begin{align} \mathbf{I_i} & = \left({g_i \ast_{\mathcal{M}} f} \right)\left({\frac{1}{\left|{x}\right|}} \right) \\[0.2cm] & = \int_{0}^{+\infty} g_i\left({w} \right) \, f\left({\frac{1}{\left|{x}\right|w}} \right) \, \frac{dw}{w} \\[0.2cm] & = \int_{0}^{+\infty} g_i\left({w} \right) \, \frac{w^{\frac{n}{2}+1} \left|{x}\right|^{\frac{n}{2}+1}}{\left({2\pi} \right)^{\frac{n}{2}} \left|{x}\right|^{n}} \, J_{{\frac{n}{2}-1}}\left({\left|{x}\right|w}\right) \, \frac{dw}{w} \\[0.2cm] & = \frac{\left|{x}\right|^{1-\frac{n}{2}}}{\left({2\pi} \right)^{\frac{n}{2}}} \, \int_{0}^{+\infty} g_i\left({w} \right) \, w^{\frac{n}{2}} \, J_{{\frac{n}{2}-1}}\left({\left|{x}\right|w}\right) \, dw. \end{align}$ $

(3.23)

From the relations Eqs (2.12) and (2.11), we have for $ i = 1, 2, 3, 4 $

$\begin{align} & \mathcal{M}\left\{{\mathbf{I_i}}\right\}\left({s}\right) \, = \mathcal{M}\left\{{\left({g_i \ast_{\mathcal{M}} f} \right)\left({\frac{1}{\left|{x}\right|}} \right)}\right\}\left({s}\right) \, = \mathcal{M}\left\{{g_i}\right\}\left({-s}\right) \, \mathcal{M}\left\{{f}\right\}\left({-s}\right) \end{align}$ $

which is equivalent to

$\begin{align} & \mathcal{M}\left\{{\mathbf{I_i}}\right\}\left({-s}\right) \, = \mathcal{M}\left\{{g_i}\right\}\left({s}\right) \, \mathcal{M}\left\{{f}\right\}\left({s}\right), \quad i = 1, 2, 3, 4. \end{align}$ $

(3.24)

Now, we compute the Mellin transforms that appear in (3.24). The Mellin transform of the function $ f $ was already calculated in ^[46] (see formula (43)):

$\begin{align} \mathcal{M}\left\{{f}\right\}\left({s}\right) \, = \frac{1}{\pi^{\frac{n-1}{2}} \, \left|{x}\right|^n \, 2^{n-1}} \, \frac{\Gamma\left({n-s} \right)}{\Gamma\left({\frac{n+1-s}{2}} \right) \, \Gamma\left({\frac{s}{2}} \right)}. \end{align}$ $

(3.25)

To compute the Mellin transform of the function $ g_1, $ we take into account Eqs (2.9), (3.15) and (3.18), obtaining

$\begin{align} \mathcal{M}\left\{{g_1}\right\}\left({s}\right) & = \int_{0}^{+\infty} w^{s-1} \, K_1\left({w, r} \right) \, dw \\[0.2cm] & = \int_{0}^{+\infty} w^{s-1} \, \frac{\rho_1^\ast \left[{\left({A +w^2} \right) \sin\left({\gamma_1^\ast \pi} \right) -B \, \cos\left({\gamma_1^\ast \pi} \right)} \right]}{ \left({A +w^2} \right)^2 +B^2} \, dw \\[0.2cm] & = \rho_1^\ast \, \sin\left({\gamma_1^\ast \pi} \right) \, \int_{0}^{+\infty} \frac{w^{s+1}}{\left({A +w^2} \right)^2 +B^2} \, dw \\[0.2cm] & \quad +\rho_1^\ast \left[{A \, \sin\left({\gamma_1^\ast \pi} \right) -B \, \cos\left({\gamma_1^\ast \pi} \right)} \right] \, \int_{0}^{+\infty} \frac{w^{s-1}}{\left({A +w^2} \right)^2 +B^2} \, dw. \end{align}$ $

(3.26)

Considering the change of variables $ w^2 = z $ in Eq (3.26) we obtain

$\begin{align} \mathcal{M}\left\{{g_1}\right\}\left({s}\right) & = \rho_1^\ast \, \sin\left({\gamma_1^\ast \pi} \right) \, \underbrace{\int_{0}^{+\infty} \frac{z^{\frac{s}{2}}}{z^2+2Az+A^2+B^2} \, dz}_{\mathbf{I_5}} \\[0.2cm] & \quad +\rho_1^\ast \left[{A \, \sin\left({\gamma_1^\ast \pi} \right) -B \, \cos\left({\gamma_1^\ast \pi} \right)} \right] \, \underbrace{\int_{0}^{+\infty} \frac{z^{\frac{s}{2}-1}}{z^2+2Az+A^2+B^2} \, dz}_{\mathbf{I_6}}. \end{align}$ $

(3.27)

Integrals $ \mathbf{I_5} $ and $ \mathbf{I_6} $ were already calculated in ^[46] (see formulas (49) and (50)). Therefore, we have that

$\begin{align} \mathbf{I_5} \, = -\frac{\pi}{\sin\left({\psi} \right)} \, \frac{\Gamma\left({1+\frac{s}{2}} \right) \, \Gamma\left({1-\left({1+\frac{s}{2}} \right)} \right)}{\Gamma\left({\frac{s\psi}{2\pi}} \right) \, \Gamma\left({1-\frac{s\psi}{2\pi}} \right)} \, \left({A^2+B^2} \right)^{\frac{s}{4}-\frac{1}{2}} \end{align}$ $

(3.28)

and

$\begin{align} \mathbf{I_6} \, = -\frac{\pi}{\sin\left({\psi} \right)} \, \frac{\Gamma\left({\frac{s}{2}} \right) \, \Gamma\left({1-\frac{s}{2}} \right)}{\Gamma\left({\frac{\psi}{\pi}\left({\frac{s}{2}-1} \right)} \right) \, \Gamma\left({1-\frac{\psi}{\pi}\left({\frac{s}{2}-1} \right)} \right)} \, \left({A^2+B^2} \right)^{\frac{s}{4}-1}, \end{align}$ $

(3.29)

where

$\begin{align} \psi = \arccos\left({\frac{A}{\sqrt{A^2+B^2}}} \right). \end{align}$ $

(3.30)

Hence, from Eqs (3.28) and (3.29) we conclude that Eq (3.27) takes the form

$\begin{align} \mathcal{M}\left\{{g_1}\right\}\left({s}\right) & = \frac{-\pi\rho_1^\ast \, \sin\left({\gamma_1^\ast \pi} \right)}{2\sin\left({\psi} \right)} \, \frac{\Gamma\left({1+\frac{s}{2}} \right) \, \Gamma\left({1-\left({1+\frac{s}{2}} \right)} \right)}{\Gamma\left({\frac{s\psi}{2\pi}} \right) \, \Gamma\left({1-\frac{s\psi}{2\pi}} \right)} \, \left({A^2+B^2} \right)^{\frac{s}{4}-\frac{1}{2}} \\[0.2cm] & \; -\frac{\pi\rho_1^\ast \left[{A \, \sin\left({\gamma_1^\ast \pi} \right) -B \, \cos\left({\gamma_1^\ast \pi} \right)} \right]}{2\sin\left({\psi} \right)} \, \frac{\Gamma\left({\frac{s}{2}} \right) \, \Gamma\left({1-\frac{s}{2}} \right)}{\Gamma\left({\frac{\psi}{\pi}\left({\frac{s}{2}-1} \right)} \right) \, \Gamma\left({1-\frac{\psi}{\pi}\left({\frac{s}{2}-1} \right)} \right)} \, \left({A^2+B^2} \right)^{\frac{s}{4}-1}. \end{align}$ $

(3.31)

Now, we calculate the Mellin transform of $ g_2 $. Taking into account Eqs (2.9), (3.16)–(3.18) and (3.30) we get

$\begin{align} & \mathcal{M}\left\{{g_2}\right\}\left({s}\right) \\[0.2cm] & = \int_{0}^{+\infty} w^{s-1} \, K_2\left({-1, w, r} \right) \, dw -\frac{d^2}{c^2} \int_{0}^{+\infty} w^{s-1} \, K_3\left({-1, w, r} \right) \, dw \\[0.2cm] & = \int_{0}^{+\infty} w^{s-1} \, \frac{\rho_2^\ast \left[{\left({A +w^2} \right) \sin\left({\gamma_2^\ast \pi} \right) -B \, \cos\left({\gamma_2^\ast \pi} \right)} \right]}{\left({-r} \right)^{-1} \, \left[{\left({A +w^2} \right)^2 +B^2} \right]} \, dw -\frac{d^2}{c^2} \, \int_{0}^{+\infty} w^{s-1} \, \frac{-B}{\left({-r} \right)^{-1} \, \left[{\left({A +w^2} \right)^2 +B^2} \right]} \, dw \end{align}$ $

(3.32)

$\begin{align} [0.2cm] & = -r \rho_2^\ast \sin\left({\gamma_2^\ast \pi} \right) \, \int_{0}^{+\infty} \frac{w^{s+1}}{\left({A +w^2} \right)^2 +B^2} \, dw -r\rho_2^\ast \left[{A\sin\left({\gamma_2^\ast \pi} \right)-B\cos\left({\gamma_2^\ast \pi} \right)} \right] \, \int_{0}^{+\infty} \frac{w^{s-1}}{\left({A +w^2} \right)^2 +B^2} \, dw \\[0.2cm] & \quad -\frac{rd^2B}{c^2} \, \int_{0}^{+\infty} \frac{w^{s-1}}{\left({A +w^2} \right)^2 +B^2} \, dw \\[0.2cm] & = -r\rho_2^\ast \sin\left({\gamma_2^\ast \pi} \right) \, \int_{0}^{+\infty} \frac{w^{s+1}}{\left({A +w^2} \right)^2 +B^2} \, dw \\[0.2cm] & \quad -\frac{r\rho_2^\ast \, c^2 \left[{A\sin\left({\gamma_2^\ast \pi} \right) -B\cos\left({\gamma_2^\ast \pi} \right)} \right] +rd^2 B}{c^2} \, \int_{0}^{+\infty} \frac{w^{s-1}}{\left({A +w^2} \right)^2 +B^2} \, dw. \end{align}$ $

(3.33)

Considering the change of variables $ w^2 = z $ in Eq (3.33), we obtain

$\begin{align} \mathcal{M}\left\{{g_2}\right\}\left({s}\right) & = -\frac{r\rho_2^\ast \sin\left({\gamma_2^\ast \pi} \right)}{2} \, \int_{0}^{+\infty} \frac{z^{\frac{s}{2}}}{z^2+2Az+A^2+B^2} \, dz \\[0.2cm] & \quad -\frac{r\rho_2^\ast \, c^2 \left[{A\sin\left({\gamma_2^\ast \pi} \right) -B\cos\left({\gamma_2^\ast \pi} \right)} \right] +rd^2 B}{2c^2} \, \int_{0}^{+\infty} \frac{z^{\frac{s}{2}-1}}{z^2+2Az+A^2+B^2} \, dz. \end{align}$ $

(3.34)

The two integrals in Eq (3.34) correspond to $ \mathbf{I_5} $ and $ \mathbf{I_6} $. Hence, from Eqs (3.28) and (3.29) we arrive to

$\begin{align} \mathcal{M}\left\{{g_2}\right\}\left({s}\right) & = \frac{\pi r \, \rho_2^\ast \sin\left({\gamma_2^\ast \pi} \right)}{2\sin\left({\psi} \right)} \, \frac{\Gamma\left({1+\frac{s}{2}} \right) \, \Gamma\left({1-\left({1+\frac{s}{2}} \right)} \right)}{\Gamma\left({\frac{s\psi}{2\pi}} \right) \, \Gamma\left({1-\frac{s\psi}{2\pi}} \right)} \, \left({A^2+B^2} \right)^{\frac{s}{4}-\frac{1}{2}} \\[0.2cm] & \quad +\frac{\pi r \left[{\rho_2^\ast \, c^2 \left[{A\sin\left({\gamma_2^\ast \pi} \right) -B\cos\left({\gamma_2^\ast \pi} \right)} \right] +d^2 B} \right]}{2c^2 \sin\left({\psi} \right)} \, \frac{\Gamma\left({\frac{s}{2}} \right) \, \Gamma\left({1-\frac{s}{2}} \right)}{\Gamma\left({\frac{\psi}{\pi}\left({\frac{s}{2}-1} \right)} \right) \, \Gamma\left({1-\frac{\psi}{\pi}\left({\frac{s}{2}-1} \right)} \right)} \, \left({A^2+B^2} \right)^{\frac{s}{4}-1}. \end{align}$ $

(3.35)

For the calculation of the Mellin transform of $ g_3 $ we use Eqs (2.9), (3.16)–(3.18) and (3.30) to get

$\begin{align} & \mathcal{M}\left\{{g_3}\right\}\left({s}\right) \\[0.2cm] & = \int_{0}^{+\infty} w^{s-1} \, K_2\left({0, w, r} \right) \, dw -\frac{d^2}{c^2} \int_{0}^{+\infty} w^{s-1} \, K_3\left({0, w, r} \right) \, dw \\[0.2cm] & = \int_{0}^{+\infty} w^{s-1} \, \frac{\rho_2^\ast \left[{\left({A +w^2} \right) \sin\left({\gamma_2^\ast \pi} \right) -B \, \cos\left({\gamma_2^\ast \pi} \right)} \right]}{\left({-r} \right)^0 \, \left[{\left({A +w^2} \right)^2 +B^2} \right]} \, dw -\frac{d^2}{c^2} \, \int_{0}^{+\infty} w^{s-1} \, \frac{-B}{\left({-r} \right)^0 \, \left[{\left({A +w^2} \right)^2 +B^2} \right]} \, dw. \end{align}$ $

(3.36)

Expression Eq (3.36) is very similar to Eq (3.32) with a difference in the power of $ -r $. However, this exponent does not affect any of the performed calculations in obtaining Eq (3.35). Then we get

$\begin{align} \mathcal{M}\left\{{g_3}\right\}\left({s}\right) & = \frac{-\pi \, \rho_2^\ast \sin\left({\gamma_2^\ast \pi} \right)}{2\sin\left({\psi} \right)} \, \frac{\Gamma\left({1+\frac{s}{2}} \right) \, \Gamma\left({1-\left({1+\frac{s}{2}} \right)} \right)}{\Gamma\left({\frac{s\psi}{2\pi}} \right) \, \Gamma\left({1-\frac{s\psi}{2\pi}} \right)} \, \left({A^2+B^2} \right)^{\frac{s}{4}-\frac{1}{2}} \end{align}$ $

$\begin{align} & -\frac{\pi \left[{\rho_2^\ast \, c^2 \left[{A\sin\left({\gamma_2^\ast \pi} \right) -B\cos\left({\gamma_2^\ast \pi} \right)} \right] +d^2 B} \right]}{2c^2 \sin\left({\psi} \right)} \, \frac{\Gamma\left({\frac{s}{2}} \right) \, \Gamma\left({1-\frac{s}{2}} \right)}{\Gamma\left({\frac{\psi}{\pi}\left({\frac{s}{2}-1} \right)} \right) \, \Gamma\left({1-\frac{\psi}{\pi}\left({\frac{s}{2}-1} \right)} \right)} \, \left({A^2+B^2} \right)^{\frac{s}{4}-1}. \end{align}$ $

(3.37)

Finally, we calculate the Mellin transform of $ g_4 $. Taking into account Eqs (2.9), (3.17), (3.18) and (3.30) we get

$\begin{align} & \mathcal{M}\left\{{g_4}\right\}\left({s}\right) \, = \int_{0}^{+\infty} w^{s-1} \, K_3\left({0, w, r} \right) \, dw \, = -B \, \int_{0}^{+\infty} \frac{w^{s-1}}{\left({A +w^2} \right)^2 +B^2} \, dw. \end{align}$ $

(3.38)

Considering the change of variables $ w^2 = z $ in Eq (3.38), we obtain

$\begin{align} & \mathcal{M}\left\{{g_4}\right\}\left({s}\right) \, = -\frac{B}{2} \, \int_{0}^{+\infty} \frac{z^{\frac{s}{2}-1}}{z^2+2Az+A^2+B^2} \, dz. \end{align}$ $

(3.39)

The integral in Eq (3.39) corresponds to the integral $ \mathbf{I_6} $. Hence, from Eq (3.29) we arrive to

$\begin{align} & \mathcal{M}\left\{{g_4}\right\}\left({s}\right) \, = \frac{B\pi}{2 \sin\left({\psi} \right)} \, \frac{\Gamma\left({\frac{s}{2}} \right) \, \Gamma\left({1-\frac{s}{2}} \right)}{\Gamma\left({\frac{\psi}{\pi}\left({\frac{s}{2}-1} \right)} \right) \, \Gamma\left({1-\frac{\psi}{\pi}\left({\frac{s}{2}-1} \right)} \right)} \, \left({A^2+B^2} \right)^{\frac{s}{4}-1}. \end{align}$ $

(3.40)

Now, using the inverse Mellin transform Eq (2.10) applied to (3.24), we obtain the representation of the integrals $ \mathbf{I_1} $, $ \mathbf{I_2} $, $ \mathbf{I_3}, $ and $ \mathbf{I_4} $ in terms of Mellin-Barnes integrals and, consequently, as Fox H-functions. For the integral $ \mathbf{I_1} $, taking into account Eqs (2.10), (3.18), (3.31) and (3.25), we obtain

$\begin{align} \mathbf{I_1} & = \frac{-\rho_1^\ast \, \sin\left({\gamma_1^\ast \pi} \right) \left({A^2+B^2} \right)^{-\frac{1}{2}}}{\pi^{\frac{n-3}{2}} \left({2\left|{x}\right|} \right)^n \, \sin\left({\psi} \right)} \, \frac{1}{2\pi i} \, \int_{\gamma-i\infty}^{\gamma+i\infty} \frac{\Gamma\left({1+\frac{s}{2}} \right) \, \Gamma\left({n-s} \right) \, \Gamma\left({-\frac{s}{2}} \right)}{\Gamma\left({\frac{s}{2}} \right) \, \Gamma\left({\frac{\psi s}{2\pi}} \right) \, \Gamma\left({\frac{n+1}{2}-\frac{s}{2}} \right) \, \Gamma\left({1-\frac{\psi s}{2\pi}} \right)} \, \left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right)^{-s} \, ds \\[0.2cm] & \quad -\frac{\rho_1^\ast \left[{A \, \sin\left({\gamma_1^\ast \pi} \right) -B \, \cos\left({\gamma_1^\ast \pi} \right)} \right] \left({A^2+B^2} \right)^{-1}}{\pi^{\frac{n-3}{2}} \left({2\left|{x}\right|} \right)^n \, \sin\left({\psi} \right)} \\[0.2cm] & \qquad \qquad \qquad \qquad \qquad \times \frac{1}{2\pi i} \, \int_{\gamma-i\infty}^{\gamma+i\infty} \frac{\Gamma\left({n-s} \right) \, \Gamma\left({1-\frac{s}{2}} \right)}{\Gamma\left({-\frac{\psi}{\pi}+\frac{\psi s}{2\pi}} \right) \, \Gamma\left({\frac{n+1}{2}-\frac{s}{2}} \right) \, \Gamma\left({1+\frac{\psi}{\pi}-\frac{\psi s}{2\pi}} \right)} \, \left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right)^{-s} \, ds \end{align}$ $

which is equivalent, by Eq (2.13), to the following expression in terms of Fox H-functions

$\begin{align} & \; -\frac{\rho_1^\ast \left[{A \, \sin\left({\gamma_1^\ast \pi} \right) -B \, \cos\left({\gamma_1^\ast \pi} \right)} \right] \left({A^2+B^2} \right)^{-1}}{\pi^{\frac{n-3}{2}} \left({2\left|{x}\right|} \right)^n \, \sin\left({\psi} \right)} \, H_{{3, 2}}^{{0, 2}} \left[\begin{array}{c|c} \begin{array}{c} \!\!\! {\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \!\! \end{array} & \begin{array}{c} \!\! {\left({1-n, \, 1} \right), \, \left({0, \, \frac{1}{2}} \right), \, \left({-\frac{\psi}{\pi}, \, \frac{\psi}{2\pi}} \right)} \!\!\! \\[0.5 cm] \!\! {\left({\frac{1-n}{2}, \, \frac{1}{2}} \right), \, \left({-\frac{\psi}{\pi}, \, \frac{\psi}{2\pi}} \right)} \!\!\! \end{array} \end{array}\right]. \end{align}$ $

(3.41)

For the integral $ \mathbf{I_2} $, taking into account Eqs(2.10), (3.18), (3.35) and (3.25), we obtain

$\begin{align} \mathbf{I_2} & = \frac{r\rho_2^\ast \, \sin\left({\gamma_2^\ast \pi} \right) \left({A^2+B^2} \right)^{-\frac{1}{2}}}{\pi^{\frac{n-3}{2}} \left({2\left|{x}\right|} \right)^n \, \sin\left({\psi} \right)} \, \frac{1}{2\pi i} \, \int_{\gamma-i\infty}^{\gamma+i\infty} \frac{\Gamma\left({1+\frac{s}{2}} \right) \, \Gamma\left({n-s} \right) \, \Gamma\left({-\frac{s}{2}} \right)}{\Gamma\left({\frac{s}{2}} \right) \, \Gamma\left({\frac{\psi s}{2\pi}} \right) \, \Gamma\left({\frac{n+1}{2}-\frac{s}{2}} \right) \, \Gamma\left({1-\frac{\psi s}{2\pi}} \right)} \, \left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right)^{-s} \, ds \\[0.2cm] & \qquad+\frac{r\left[{\rho_2^\ast \, c^2\left({A \, \sin\left({\gamma_2^\ast \pi} \right) -B \, \cos\left({\gamma_2^\ast \pi} \right)} \right)+Bd^2} \right] \left({A^2+B^2} \right)^{-1}}{c^2 \, \pi^{\frac{n-3}{2}} \left({2\left|{x}\right|} \right)^n \, \sin\left({\psi} \right)} \\[0.2cm] & \qquad \qquad \times \frac{1}{2\pi i} \, \int_{\gamma-i\infty}^{\gamma+i\infty} \frac{\Gamma\left({n-s} \right) \, \Gamma\left({1-\frac{s}{2}} \right)}{\Gamma\left({-\frac{\psi}{\pi}+\frac{\psi s}{2\pi}} \right) \, \Gamma\left({\frac{n+1}{2}-\frac{s}{2}} \right) \, \Gamma\left({1+\frac{\psi}{\pi}-\frac{\psi s}{2\pi}} \right)} \, \left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right)^{-s} \, ds \end{align}$ $

which is equivalent, by Eq (2.13), to the following expression in terms of Fox H-functions

$\begin{align} \mathbf{I_2} & = \frac{r\rho_2^\ast \, \sin\left({\gamma_2^\ast \pi} \right) \left({A^2+B^2} \right)^{-\frac{1}{2}}}{\pi^{\frac{n-3}{2}} \left({2\left|{x}\right|} \right)^n \, \sin\left({\psi} \right)} \, H_{{4, 3}}^{{1, 2}} \left[\begin{array}{c|c} \begin{array}{c} \!\!\! {\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \!\! \end{array} & \begin{array}{c} \!\! {\left({1-n, \, 1} \right), \, \left({1, \, \frac{1}{2}} \right), \, \left({0, \, \frac{1}{2}} \right), \, \left({0, \, \frac{\psi}{2\pi}} \right)} \!\!\! \\[0.5 cm] \!\! {\left({1, \, \frac{1}{2}} \right), \, \left({\frac{1-n}{2}, \, \frac{1}{2}} \right), \, \left({0, \, \frac{\psi}{2\pi}} \right)} \!\!\! \end{array} \end{array}\right] \\[0.2cm] & \qquad +\frac{r\left[{\rho_2^\ast \, c^2\left({A \, \sin\left({\gamma_2^\ast \pi} \right) -B \, \cos\left({\gamma_2^\ast \pi} \right)} \right)+Bd^2} \right] \left({A^2+B^2} \right)^{-1}}{c^2 \, \pi^{\frac{n-3}{2}} \left({2\left|{x}\right|} \right)^n \, \sin\left({\psi} \right)} \\[0.2cm] & \qquad \qquad \times H_{{3, 2}}^{{0, 2}} \left[\begin{array}{c|c} \begin{array}{c} \!\!\! {\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \!\! \end{array} & \begin{array}{c} \!\! {\left({1-n, \, 1} \right), \, \left({0, \, \frac{1}{2}} \right), \, \left({-\frac{\psi}{\pi}, \, \frac{\psi}{2\pi}} \right)} \!\!\! \\[0.5 cm] \!\! {\left({\frac{1-n}{2}, \, \frac{1}{2}} \right), \, \left({-\frac{\psi}{\pi}, \, \frac{\psi}{2\pi}} \right)} \!\!\! \end{array} \end{array}\right]. \end{align}$ $

(3.42)

Due to the similarities between $ g_2 $ and $ g_3 $ (and consequently between $ \mathbf{I_2} $ and $ \mathbf{I_3} $) we have that

$\begin{align} \mathbf{I_3} & = \frac{-\rho_2^\ast \, \sin\left({\gamma_2^\ast \pi} \right) \left({A^2+B^2} \right)^{-\frac{1}{2}}}{\pi^{\frac{n-3}{2}} \left({2\left|{x}\right|} \right)^n \, \sin\left({\psi} \right)} \, H_{{4, 3}}^{{1, 2}} \left[\begin{array}{c|c} \begin{array}{c} \!\!\! {\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \!\! \end{array} & \begin{array}{c} \!\! {\left({1-n, \, 1} \right), \, \left({1, \, \frac{1}{2}} \right), \, \left({0, \, \frac{1}{2}} \right), \, \left({0, \, \frac{\psi}{2\pi}} \right)} \!\!\! \\[0.5 cm] \!\! {\left({1, \, \frac{1}{2}} \right), \, \left({\frac{1-n}{2}, \, \frac{1}{2}} \right), \, \left({0, \, \frac{\psi}{2\pi}} \right)} \!\!\! \end{array} \end{array}\right] \\[0.2cm] & \qquad -\frac{\left[{\rho_2^\ast \, c^2\left({A \, \sin\left({\gamma_2^\ast \pi} \right) -B \, \cos\left({\gamma_2^\ast \pi} \right)} \right)+Bd^2} \right] \left({A^2+B^2} \right)^{-1}}{c^2 \, \pi^{\frac{n-3}{2}} \left({2\left|{x}\right|} \right)^n \, \sin\left({\psi} \right)} \\[0.2cm] & \qquad \qquad \times H_{{3, 2}}^{{0, 2}} \left[\begin{array}{c|c} \begin{array}{c} \!\!\! {\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \!\! \end{array} & \begin{array}{c} \!\! {\left({1-n, \, 1} \right), \, \left({0, \, \frac{1}{2}} \right), \, \left({-\frac{\psi}{\pi}, \, \frac{\psi}{2\pi}} \right)} \!\!\! \\[0.5 cm] \!\! {\left({\frac{1-n}{2}, \, \frac{1}{2}} \right), \, \left({-\frac{\psi}{\pi}, \, \frac{\psi}{2\pi}} \right)} \!\!\! \end{array} \end{array}\right]. \end{align}$ $

(3.43)

Finally, for the integral $ \mathbf{I_4} $, taking into account Eqs (2.10), (3.18), (3.40) and (3.25), we obtain

$\begin{align} \mathbf{I_4} & = \frac{B \left({A^2+B^2} \right)^{-1}}{\pi^{\frac{n-3}{2}} \left({2\left|{x}\right|} \right)^n \, \sin\left({\psi} \right)} \, \frac{1}{2\pi i} \, \int_{\gamma-i\infty}^{\gamma+i\infty} \frac{\Gamma\left({n-s} \right) \, \Gamma\left({1-\frac{s}{2}} \right)}{\Gamma\left({-\frac{\psi}{\pi}+\frac{\psi s}{2\pi}} \right) \, \Gamma\left({\frac{n+1}{2}-\frac{s}{2}} \right) \, \Gamma\left({1+\frac{\psi}{\pi}-\frac{\psi s}{2\pi}} \right)} \, \left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right)^{-s} \, ds \end{align}$ $

which is equivalent, by (2.13), to the following expression in terms of Fox H-functions

$\begin{align} \mathbf{I_4} & = \frac{B \left({A^2+B^2} \right)^{-1}}{\pi^{\frac{n-3}{2}} \left({2\left|{x}\right|} \right)^n \, \sin\left({\psi} \right)} \, H_{{3, 2}}^{{0, 2}} \left[\begin{array}{c|c} \begin{array}{c} \!\!\! {\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \!\! \end{array} & \begin{array}{c} \!\! {\left({1-n, \, 1} \right), \, \left({0, \, \frac{1}{2}} \right), \, \left({-\frac{\psi}{\pi}, \, \frac{\psi}{2\pi}} \right)} \!\!\! \\[0.5 cm] \!\! {\left({\frac{1-n}{2}, \, \frac{1}{2}} \right), \, \left({-\frac{\psi}{\pi}, \, \frac{\psi}{2\pi}} \right)} \!\!\! \end{array} \end{array}\right]. \end{align}$ $

(3.44)

From Eqs (3.41)–(3.44) we conclude that the representation (3.22) of the solution $ u\left({x, t} \right) $ of Eqs (3.1) and (3.2) corresponds to the sum of convolution integrals involving Fox H-functions.

In the next subsection we summarize our calculations in the main result of the paper.

3.3. Main result and corollary

Taking into account Eqs (3.22) and (3.41)–(3.44) we obtain our main result.

Theorem 3.3. The solution of the time-fractional telegraph equation of distributed order Eq (3.1) subject to the conditions Eqs (3.3) and (3.2) and the additional assumption Eq (3.11) is given, in terms of convolution integrals, by

$\begin{align} u\left({x, t} \right) & = \int_{ \mathbb{R}^n} f\left({z} \right) \, G_1\left({x-z, \, t} \right) \, dz +\int_{ \mathbb{R}^n} g_1\left({z} \right) \, G_2\left({x-z, \, t} \right) \, dz \\[0.2cm] & \quad +\int_{ \mathbb{R}^n} g_2\left({z} \right) \, G_3\left({x-z, \, t} \right) \, dz +\int_{ \mathbb{R}^n} \, \int_{0}^{t} q\left({z, \, w} \right) \, G_4\left({x-z, \, t-w} \right) \, dw \, dz, \end{align}$ $

(3.45)

where the functions $ G_1 $, $ G_2 $, $ G_3 $ and $ G_4 $ are given by

$\begin{align} G_1\left({x, t} \right) & = \frac{1}{\pi^{\frac{n-1}{2}} \left({2\left|{x}\right|} \right)^n} \, \int_{0}^{+\infty} \frac{\rho_1^\ast \left({A^2+B^2} \right)^{-\frac{1}{2}} \, e^{-rt}}{\sin\left({\psi} \right)} \\[0.2cm] & \times \left[{\sin\left({\gamma_1^\ast \pi} \right) \, \mathcal{H}\left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right) +\left[{A \, \sin\left({\gamma_1^\ast \pi} \right) -B \, \cos\left({\gamma_1^\ast \pi} \right)} \right] \left({A^2+B^2} \right)^{-\frac{1}{2}} \, \mathcal{H}^\ast \left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right)} \right] \, dr, \\[0.2cm] G_2\left({x, t} \right) & = \frac{-1}{\pi^{\frac{n-1}{2}} \left({2\left|{x}\right|} \right)^n} \, \int_{0}^{+\infty} \frac{r\left({A^2+B^2} \right)^{-\frac{1}{2}} \, e^{-rt}}{\sin\left({\psi} \right)} \left[\rho_2^\ast \sin\left({\gamma_2^\ast \pi} \right) \, \mathcal{H}\left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right) \right. \\[0.2cm] & \qquad \left.+\frac{1}{c^2} \left[{\rho_2^\ast \, c^2 \left({A \, \sin\left({\gamma_2^\ast \pi} \right) -B \, \cos\left({\gamma_2^\ast \pi} \right)} \right) +Bd^2} \right] \left({A^2+B^2} \right)^{-\frac{1}{2}} \, \mathcal{H}^\ast \left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right)\right] \, dr, \\[0.2cm] G_3\left({x, t} \right) & = \frac{1}{\pi^{\frac{n-1}{2}} \left({2\left|{x}\right|} \right)^n} \, \int_{0}^{+\infty} \frac{\left({A^2+B^2} \right)^{-\frac{1}{2}} \, e^{-rt}}{\sin\left({\psi} \right)} \left[\rho_2^\ast \sin\left({\gamma_2^\ast \pi} \right) \, \mathcal{H}\left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right) \right. \\[0.2cm] & \qquad \left.+\frac{1}{c^2} \left[{\rho_2^\ast \, c^2 \left({A \, \sin\left({\gamma_2^\ast \pi} \right) -B \, \cos\left({\gamma_2^\ast \pi} \right)} \right) +Bd^2} \right] \left({A^2+B^2} \right)^{-\frac{1}{2}} \, \mathcal{H}^\ast \left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right)\right] \, dr, \\[0.2cm] G_4\left({x, t} \right) & = \frac{-1}{c^2 \, \pi^{\frac{n-1}{2}} \left({2\left|{x}\right|} \right)^n} \, \int_{0}^{+\infty} \frac{B \left({A^2+B^2} \right)^{-1} \, e^{-rt}}{\sin\left({\psi} \right)} \, \mathcal{H}^\ast \left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right)\, dr, \end{align}$ $

where $ \rho_1^\ast, $ $ \gamma_1^\ast $, $ \rho_2^\ast, $ and $ \gamma_2^\ast $, $ A $ and $ B $, and $ \psi $ are given, respectively, by Eq (3.14), (3.18) and (3.30). Moreover, the functions $ \mathcal{H} $ and $ \mathcal{H}^\ast $ are expressed in terms of the following Fox H-functions

$\begin{align} & \mathcal{H}\left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right) \, = H_{{4, 3}}^{{1, 2}} \left[\begin{array}{c|c} \begin{array}{c} \!\!\! {\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \!\! \end{array} & \begin{array}{c} \!\! {\left({1-n, \, 1} \right), \, \left({1, \, \frac{1}{2}} \right), \, \left({0, \, \frac{1}{2}} \right), \, \left({0, \, \frac{\psi}{2\pi}} \right)} \!\!\! \\[0.5 cm] \!\! {\left({1, \, \frac{1}{2}} \right), \, \left({\frac{1-n}{2}, \, \frac{1}{2}} \right), \, \left({0, \, \frac{\psi}{2\pi}} \right)} \!\!\! \end{array} \end{array}\right], \\[0.2cm] & \mathcal{H}^\ast \left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right) \, = H_{{3, 2}}^{{0, 2}} \left[\begin{array}{c|c} \begin{array}{c} \!\!\! {\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \!\! \end{array} & \begin{array}{c} \!\! {\left({1-n, \, 1} \right), \, \left({0, \, \frac{1}{2}} \right), \, \left({-\frac{\psi}{\pi}, \, \frac{\psi}{2\pi}} \right)} \!\!\! \\[0.5 cm] \!\! {\left({\frac{1-n}{2}, \, \frac{1}{2}} \right), \, \left({-\frac{\psi}{\pi}, \, \frac{\psi}{2\pi}} \right)} \!\!\! \end{array} \end{array}\right]. \end{align}$ $

Remark 3.4. If we consider

$\begin{align} & f\left({x} \right) \, = \delta\left({x} \right) \, = \prod\limits_{i = 1}^{n} \delta\left({x_i} \right), \qquad \; g\left({x} \right) \, = q\left({x, t} \right) = 0, \qquad \; a\, = c \, = 1, \qquad \; d = \sqrt{\lambda} \end{align}$ $

with $ \lambda \in \mathbb{R}^+ $ in Eqs (3.1) and (3.2), then the solution $ u\left({x, t} \right) $ given by Eq (3.45) corresponds to the eigenfunctions of the generalized time-fractional telegraph equation of distributed order in $ \mathbb{R}^n \times \mathbb{R}^+ $. Moreover, if additionally $ b_2\left({\beta, \nu} \right) = 0 $ (resp. $ b_1\left({\alpha, \mu} \right) = 0 $) we obtain the representation of the generalized eigenfunctions of the time-fractional diffusion (resp. wave) equation of distributed order in $ \mathbb{R}^n \times \mathbb{R}^+ $.

Putting $ a = 0 $ in Theorem 3.3, we have the following simplifications

$\begin{align} B_1\left({s} \right) \, = B_1^\ast\left({s} \right) \, = 0, \qquad A = \rho \cos\left({\gamma\pi} \right), \qquad B = \rho \sin\left({\gamma\pi} \right), \qquad A^2+B^2 = \rho^2, \qquad \psi = \gamma\pi, \end{align}$ $

which give the following result.

Corollary 3.5. The solution of the generalized time-fractional wave equation of distributed order in $ \mathbb{R}^n \times \mathbb{R}^+ $

$\begin{align} & \int_{0}^{1}\int_{1}^{2} b_2\left({\beta, \nu} \right) \, {}_{{t}}\partial_{{0^+}}^{{\beta}, {\nu}} u\left({x, t} \right) \, d\beta \, d\nu -c^2 \, \Delta_x u\left({x, t} \right) +d^2 \, u\left({x, t} \right) \, = q\left({x, t} \right) \end{align}$ $

for a given density function $ b_2\left({\beta, \nu} \right) $, subject to the following initial and boundary conditions

$\begin{align} & \left({{}_{{t}}I_{{0^+}}^{{\left({1-\nu} \right)\left({2-\beta} \right)}}u} \right)\left({x, 0^+} \right) = g_1\left({x} \right), \qquad \left[{\frac{\partial}{\partial t}\left({{}_{{t}}I_{{0^+}}^{{\left({1-\nu} \right)\left({2-\beta} \right)}}u} \right)} \right]\left({x, 0^+} \right) = g_2\left({x} \right), \qquad \lim\limits_{|x|\to +\infty} u\left({x, t} \right) = 0, \end{align}$ $

is given, in terms of convolution integrals, by

$\begin{align} u\left({x, t} \right) \! = \!\!\!\int_{ \mathbb{R}^n} g_1\left({z} \right) \, G_2\left({x-z, \, t} \right) \, dz +\!\!\!\int_{ \mathbb{R}^n} g_2\left({z} \right) \, G_3\left({x-z, \, t} \right) \, dz +\!\!\!\int_{ \mathbb{R}^n} \int_{0}^{t} q\left({z, \, w} \right) \, G_4\left({x-z, \, t-w} \right) \, dw \, dz, \end{align}$ $

where the functions $ G_2 $, $ G_3 $, and $ G_4 $ are given by

$\begin{align} G_2\left({x, t} \right) & = \frac{-1}{\pi^{\frac{n-1}{2}} \left({2\left|{x}\right|} \right)^n} \, \int_{0}^{+\infty} \frac{r e^{-rt}}{\rho \sin\left({\gamma\pi} \right)} \left[{\rho^\ast \sin\left({\gamma^\ast \pi} \right) \mathcal{H}\left({\frac{1}{\left|{x}\right| \, \sqrt{\rho}}} \right) +\frac{d^2}{c^2} \, \sin\left({\gamma\pi} \right) \, \mathcal{H}^\ast \left({\frac{1}{\left|{x}\right| \, \sqrt{\rho}}} \right)} \right] \, dr, \\[0.2cm] G_3\left({x, t} \right) & = \frac{1}{\pi^{\frac{n-1}{2}} \left({2\left|{x}\right|} \right)^n} \, \int_{0}^{+\infty} \frac{e^{-rt}}{\rho \sin\left({\gamma \pi} \right)} \left[{\rho^\ast \sin\left({\gamma^\ast \pi} \right) \mathcal{H}\left({\frac{1}{\left|{x}\right| \, \sqrt{\rho}}} \right) +\frac{d^2}{c^2} \, \sin\left({\gamma\pi} \right) \, \mathcal{H}^\ast \left({\frac{1}{\left|{x}\right| \, \sqrt{\rho}}} \right)} \right] \, dr, \\[0.2cm] G_4\left({x, t} \right) & = \frac{-1}{c^2 \, \pi^{\frac{n-1}{2}} \left({2\left|{x}\right|} \right)^n} \, \int_{0}^{+\infty} \frac{e^{-rt}}{\rho} \, \mathcal{H}^\ast \left({\frac{1}{\left|{x}\right| \, \sqrt{\rho}}} \right)\, dr \end{align}$ $

with $ \rho $ and $ \gamma $, $ \rho^\ast $ and $ \gamma^\ast $ given by Eqs (3.13) and (3.14), respectively, and the functions $ \mathcal{H} $ and $ \mathcal{H}^\ast $ are expressed in terms of the following Fox H-functions

$\begin{align} & \mathcal{H}\left({\frac{1}{\left|{x}\right| \, \sqrt{\rho}}} \right) \, = H_{{3, 2}}^{{0, 2}} \left[\begin{array}{c|c} \begin{array}{c} \!\!\! {\frac{1}{\left|{x}\right| \, \sqrt{\rho}}} \!\! \end{array} & \begin{array}{c} \!\! {\left({1-n, \, 1} \right), \, \left({1, \, \frac{1}{2}} \right), \, \left({0, \, \frac{\gamma}{2}} \right)} \!\!\! \\[0.5 cm] \!\! {\left({\frac{1-n}{2}, \, \frac{1}{2}} \right), \, \left({0, \, \frac{\gamma}{2}} \right)} \!\!\! \end{array} \end{array}\right], \\[0.2cm] & \mathcal{H}^\ast \left({\frac{1}{\left|{x}\right| \, \sqrt{\rho}}} \right) \, = H_{{3, 2}}^{{0, 2}} \left[\begin{array}{c|c} \begin{array}{c} \!\!\! {\frac{1}{\left|{x}\right| \, \sqrt{\rho}}} \!\! \end{array} & \begin{array}{c} \!\! {\left({1-n, \, 1} \right), \, \left({0, \, \frac{1}{2}} \right), \, \left({-\gamma, \, \frac{\gamma}{2}} \right)} \!\!\! \\[0.5 cm] \!\! {\left({\frac{1-n}{2}, \, \frac{1}{2}} \right), \, \left({-\gamma, \, \frac{\gamma}{2}} \right)} \!\!\! \end{array} \end{array}\right]. \end{align}$ $

Remark 3.6. If we consider $ \nu = \mu = 1 $ in Theorem 3.3 (i.e., the telegraph equation has only Caputo fractional derivatives) we obtain the main result in ^[46]. For that we need to take into account Remarks 3.1 and 3.2 and to combine the first two integrals in Eq (3.45) into a unique integral. Hence, the solution $ u\left({x, t} \right) $ is given by

$\begin{align} u\left({x, t} \right) & = \int_{ \mathbb{R}^n} f\left({z} \right) \left({G_1\left({x-z, \, t} \right) +G_2\left({x-z, \, t} \right)} \right) \, dz \\[0.2cm] & \quad +\int_{ \mathbb{R}^n} g_2\left({z} \right) \, G_3\left({x-z, \, t} \right) \, dz +\int_{ \mathbb{R}^n} \, \int_{0}^{t} q\left({z, \, w} \right) \, G_4\left({x-z, \, t-w} \right) \, dw \, dz, \end{align}$ $

(3.46)

where for $ \nu = \mu = 1 $

$\begin{align} &G_1\left({x, \, t} \right) +G_2\left({x, \, t} \right) \\[0.2cm] & = \frac{-1}{\pi^{\frac{n-1}{2}} \left({2\left|{x}\right|} \right)^n} \, \int_{0}^{+\infty} \frac{\left({A^2+B^2} \right)^{-\frac{1}{2}} \, e^{-rt}}{r \, \sin\left({\psi} \right)} \left\{\left[{\rho_1 \, \sin\left({\gamma_1 \pi} \right) +\rho_2 \, \sin\left({\gamma_2 \pi} \right)} \right] \, \mathcal{H}\left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right) \right. \\[0.2cm] & \; \left.+\left[{A \, \rho_1 \, \sin\left({\gamma_1 \pi} \right) -B \, \rho_1 \, \cos\left({\gamma_1 \pi} \right) +A \, \rho_2 \, \sin\left({\gamma_2\pi} \right) -B \, \rho_2 \, \cos\left({\gamma_2\pi} \right)} \right] \left({A^2+B^2} \right)^{-\frac{1}{2}} \, \mathcal{H}^\ast \left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right)\right. \\[0.2cm] & \qquad \left.+\frac{d^2 B}{c^2}\left({A^2+B^2} \right)^{-\frac{1}{2}} \, \mathcal{H}^\ast \left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right)\right\} \, dr. \end{align}$ $

(3.47)

By Eq (3.18) we have that

$\begin{align} & A \, \rho_1 \, \sin\left({\gamma_1 \pi} \right) -B \, \rho_1 \, \cos\left({\gamma_1 \pi} \right) +A \, \rho_2 \, \sin\left({\gamma_2\pi} \right) -B \, \rho_2 \, \cos\left({\gamma_2\pi} \right) \\[0.2cm] & \qquad = A \left[{\rho_1 \, \sin\left({\gamma_1 \pi} \right) +\, \rho_2 \, \sin\left({\gamma_2\pi} \right)} \right] -B\left[{\rho_1 \, \cos\left({\gamma_1 \pi} \right) +\rho_2 \, \cos\left({\gamma_2\pi} \right)} \right] \\[0.2cm] & \qquad = AB -BA \, = 0, \end{align}$ $

and, hence, Eq (3.47) simplifies to

which corresponds to the function $ G_1 $ presented in the main result of ^[46]. Moreover, in Eq (3.46)

$\begin{align} G_3\left({x, t} \right) & = \frac{1}{\pi^{\frac{n-1}{2}} \left({2\left|{x}\right|} \right)^n} \, \int_{0}^{+\infty} \frac{\left({A^2+B^2} \right)^{-\frac{1}{2}} \, e^{-rt}}{r^2 \, \sin\left({\psi} \right)} \left[\rho_2 \sin\left({\gamma_2 \pi} \right) \, \mathcal{H}\left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right) \right. \\[0.2cm] & \qquad \left.+\frac{1}{c^2} \left[{\rho_2 \, c^2 \left({A \, \sin\left({\gamma_2 \pi} \right) -B \, \cos\left({\gamma_2 \pi} \right)} \right) +Bd^2} \right] \left({A^2+B^2} \right)^{-\frac{1}{2}} \, \mathcal{H}^\ast \left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right)\right] \, dr, \\[0.2cm] G_4\left({x, t} \right) & = \frac{1}{c^2 \, \pi^{\frac{n-1}{2}} \left({2\left|{x}\right|} \right)^n} \, \int_{0}^{+\infty} \frac{B \left({A^2+B^2} \right)^{-1} \, e^{-rt}}{\sin\left({\psi} \right)} \, \mathcal{H}^\ast \left({\frac{\left({A^2+B^2} \right)^{-\frac{1}{4}}}{\left|{x}\right|}} \right)\, dr \end{align}$ $

which correspond, respectively, to the functions $ G_2 $ and $ G_3 $ that appear in the main result of ^[46]. Therefore, we can claim that there is consistency in our results.

Remark 3.7. The telegraph equations studied in ^[38,40] are particular cases of the equation studied in this paper, for the choices $ \nu = \mu = 1, $ $ b_2\left({\beta, \nu} \right) = \delta\left({\beta-\beta_1} \right), $ $ b_1\left({\alpha, \mu} \right) = \delta\left({\alpha-\alpha_1} \right) $, with $ 1 < \beta_1 \leq 2 $ and $ 0 < \alpha_1 \leq 1 $ $ d = 0, $ and $ q\left({x, t} \right) = 0. $

The numerical implementation of Eq (3.45) is possible, however, depends substantially on the study of the asymptotic behaviour of $ G_1 $, $ G_2, $ $ G_3 $ and $ G_4 $ through the study of the asymptotic behaviour of the associated Fox H-functions. We would like to remark also that Eq (3.45) is a very general solution, but for particular cases of the dimension, of the fractional parameters, and/or of the density functions, it is possible to get simpler expressions.

4. Fractional moments

In this section we obtain the expression for some fractional moments of the first fundamental solution $ \mathbf{G_1} $ of the time-fractional telegraph equation of distributed order Eq (3.1) with $ d \, = q\left({x, t} \right) \, = 0, $ and subject to the initial and boundary conditions

$\begin{align} & f\left({x} \right) = g_1\left({x} \right) = \delta\left({x} \right) = \prod\limits_{j = 1}^{n}\delta\left({x_j} \right) \qquad \text{ and } \qquad g_2\left({x} \right) = 0 . \end{align}$ $

(4.1)

Then $ \mathbf{G_1} $ is given by $ \mathbf{G_1}\left({x, t} \right) = G_1\left({x, t} \right)+G_2\left({x, t} \right) $, where $ G_1 $ and $ G_2 $ are given in Theorem 3.3.

It is well known that the Mellin transform (2.9) can be interpreted as the fractional moment of order $ s-1 $ of the function $ f $ (see ^[62]). Therefore, we can calculate the fractional moments $ \mathbf{M}_{{n; , \gamma}}^{{\alpha, \mu; \beta, \nu}} $ of arbitrary order $ \gamma > 0 $ of $ \mathbf{\widetilde{G}_1} $, where $ \mathbf{\widetilde{G}_1} $ denotes the Laplace transform of $ \mathbf{G_1} $. Denoting by $ \mathbf{s} $ the variable in the Laplace domain and by $ r $ the radial quantity $ \left|{x}\right| $, we have, from the definition of the Mellin transform, that

$\begin{align} \widetilde{\mathbf{M}}_{{n;, \gamma}}^{{\alpha, \mu; \beta, \nu}}\left({ \mathbf{s}} \right) \, = \int_{0}^{+\infty} r^\gamma \; \mathbf{\widetilde{G}_1}\left({r, \mathbf{s}} \right) \, dr \, = \int_{0}^{+\infty} r^{\gamma-n+1-1} \, r^n \mathbf{\widetilde{G}_1}\left({r, \mathbf{s}} \right) \, dr \, = \mathcal{M}\left\{{r^n \, \mathbf{\widetilde{G}_1}\left({r, \mathbf{s}} \right)}\right\}\left({\gamma-n+1}\right). \end{align}$ $

(4.2)

From Eq (3.5), we have that

$\begin{align} \mathbf{G_1}\left({r, t} \right) & = \mathcal{L}^{-1}\left\{{\mathcal{F}^{-1}\left\{{\widehat{\widetilde{u}}_1\left({\kappa, \mathbf{s}} \right) +\widehat{\widetilde{u}}_2\left({\kappa, \mathbf{s}} \right)\Big|_{p = -1} -\frac{d^2}{c^2} \, \widehat{\widetilde{u}}_3\left({\kappa, \mathbf{s}} \right)\Big|_{p = -1}}\right\}\left({r, \mathbf{s}}\right)}\right\}\left({r, t}\right) \end{align}$ $

which is equivalent to

$\begin{align} \mathbf{\widetilde{G}_1}\left({r, \mathbf{s}} \right) \, = \mathcal{L}\left\{{ \mathbf{G_1} \left({r, t} \right)}\right\}\left({r, \mathbf{s}}\right) \, = \mathcal{F}^{-1}\left\{{\widehat{\widetilde{u}}_1\left({\kappa, \mathbf{s}} \right) +\widehat{\widetilde{u}}_2\left({\kappa, \mathbf{s}} \right)\Big|_{p = -1} -\frac{d^2}{c^2} \, \widehat{\widetilde{u}}_3\left({\kappa, \mathbf{s}} \right)\Big|_{p = -1}}\right\}\left({r, \mathbf{s}}\right). \end{align}$ $

To calculate the inverse Fourier transform we are going to use the Mellin transform, similarly as it was done in Section 3. Taking into account Eq (3.21), we have that

$\begin{align} & \mathcal{F}^{-1}\left\{{\widehat{\widetilde{u}}_1\left({\kappa, \mathbf{s}} \right) +\widehat{\widetilde{u}}_2\left({\kappa, \mathbf{s}} \right)\Big|_{p = -1} -\frac{d^2}{c^2} \, \widehat{\widetilde{u}}_3\left({\kappa, \mathbf{s}} \right)\Big|_{p = -1}}\right\}\left({r, \mathbf{s}}\right) \\[0.2cm] & \quad = \frac{r^{1-\frac{n}{2}}}{\left({2\pi} \right)^{\frac{n}{2}}} \, \int_{0}^{+\infty} \left[{\widehat{\widetilde{u}}_1\left({\kappa, \mathbf{s}} \right) +\widehat{\widetilde{u}}_2\left({\kappa, \mathbf{s}} \right)\Big|_{p = -1} -\frac{d^2}{c^2} \, \widehat{\widetilde{u}}_3\left({\kappa, \mathbf{s}} \right)\Big|_{p = -1}} \right] \, w^{\frac{n}{2}} \, J_{{\frac{n}{2}-1}}\left({\left|{x}\right| \, w}\right) \, dw \\[0.2cm] & \quad = \left({g_5 \ast_{\mathcal{M}} f} \right)\left({\frac{1}{r}} \right), \end{align}$ $

(4.3)

where $ \ast_{\mathcal{M}} $ denotes the Mellin convolution given by Eq (2.11) at the point $ \frac{1}{r} $ with

$\begin{align} & g_5\left({w} \right) \, = \widehat{\widetilde{u}}_1\left({\kappa, \mathbf{s}} \right) +\widehat{\widetilde{u}}_2\left({\kappa, \mathbf{s}} \right)\Big|_{p = -1} -\frac{d^2}{c^2} \, \widehat{\widetilde{u}}_3\left({\kappa, \mathbf{s}} \right)\Big|_{p = -1} \end{align}$ $

and

$\begin{align} & f\left({w} \right) \, = \frac{1}{\left({2\pi} \right)^{\frac{n}{2}} \, \left|{x}\right|^n \, w^{\frac{n}{2}+1}} \, J_{{\frac{n}{2}-1}}\left({\frac{1}{w}}\right). \end{align}$ $

Denoting by $ \mathbf{I_7} $ the integral in Eq (4.3), we have, by relations Eqs (2.12) and (2.11), that

$\begin{align} & \mathcal{M}\left\{{\mathbf{I_7}}\right\}\left({s}\right) \, = \mathcal{M}\left\{{\left({g_5 \ast_{\mathcal{M}} f} \right)\left({\frac{1}{r}} \right)}\right\}\left({s}\right) \, = \mathcal{M}\left\{{g_5}\right\}\left({-s}\right) \, \mathcal{M}\left\{{f}\right\}\left({-s}\right) \end{align}$ $

which is equivalent to

$\begin{align} & \mathcal{M}\left\{{\mathbf{I_7}}\right\}\left({-s}\right) \, = \mathcal{M}\left\{{g_5}\right\}\left({s}\right) \, \mathcal{M}\left\{{f}\right\}\left({s}\right). \end{align}$ $

(4.4)

From Eq (3.25) we have that

(4.5)

Now, we calculate the Mellin transform of the function $ g_5 $. Taking into account Eqs (2.9) and (3.8) with $ p = 0 $, Eqs (3.9) and (3.10) with $ p = -1 $, we get

$\begin{align} \mathcal{M}\left\{{g_5}\right\}\left({s}\right) & = \int_{0}^{+\infty} w^{s-1} \left[{\widehat{\widetilde{u}}_1\left({\kappa, \mathbf{s}} \right) +\widehat{\widetilde{u}}_2\left({\kappa, \mathbf{s}} \right)\Big|_{p = -1} -\frac{d^2}{c^2} \, \widehat{\widetilde{u}}_3\left({\kappa, \mathbf{s}} \right)\Big|_{p = -1}} \right] \, dw \\[0.2cm] & = \left[{B_1^\ast\left({ \mathbf{s}} \right) +\frac{ \mathbf{s}}{c^2} \left[{c^2 \, B_2^\ast\left({ \mathbf{s}} \right) -d^2} \right]} \right] \, \int_{0}^{+\infty} \frac{w^{s-1}}{B_2\left({ \mathbf{s}} \right) +B_1\left({ \mathbf{s}} \right) +w^2} \, dw. \end{align}$ $

The integral in the previous expression was already calculated in ^[46] (see formula (84)). Therefore, we have that

$\begin{align} \mathcal{M}\left\{{g_5}\right\}\left({s}\right) & = \left[{B_1^\ast\left({ \mathbf{s}} \right) +\frac{ \mathbf{s}}{c^2} \left[{c^2 \, B_2^\ast\left({ \mathbf{s}} \right) -d^2} \right]} \right] \, \pi \, \frac{\Gamma\left({1-s} \right) \, \Gamma\left({s} \right)}{\Gamma\left({\frac{1+s}{2}} \right) \, \Gamma\left({\frac{1-s}{2}} \right)} \, \left({B_2\left({ \mathbf{s}} \right) +B_1\left({ \mathbf{s}} \right)} \right)^{\frac{s}{2}-1}. \end{align}$ $

(4.6)

From Eqs (4.5), (4.6), (4.4) and (4.2) we conclude that

$\begin{align} & \mathcal{M}\left\{{r^n \, \mathcal{F}^{-1}\left\{{\widehat{\widetilde{u}}_1\left({\kappa, \mathbf{s}} \right) +\widehat{\widetilde{u}}_2\left({\kappa, \mathbf{s}} \right)\Big|_{p = -1} -\frac{d^2}{c^2} \, \widehat{\widetilde{u}}_3\left({\kappa, \mathbf{s}} \right)\Big|_{p = -1}}\right\}\left({r, \mathbf{s}}\right)}\right\}\left({\gamma-n+1, \mathbf{s}}\right) \\[0.2cm] & \quad = \left[{B_1^\ast\left({ \mathbf{s}} \right) +\frac{ \mathbf{s}}{c^2} \left[{c^2 \, B_2^\ast\left({ \mathbf{s}} \right) -d^2} \right]} \right] \, \frac{\left({B_2\left({ \mathbf{s}} \right) +B_1\left({ \mathbf{s}} \right)} \right)^{-\frac{s}{2}-1}}{\pi^{\frac{n-3}{2}} 2^{n-1}} \, \frac{\Gamma\left({n+s} \right) \, \Gamma\left({1+s} \right) \, \Gamma\left({-s} \right)}{\Gamma\left({\frac{n+1+s}{2}} \right) \, \Gamma\left({-\frac{s}{2}} \right) \, \Gamma\left({\frac{1-s}{2}} \right) \, \Gamma\left({\frac{1+s}{2}} \right)} \Bigg|_{s = \gamma-n+1}. \end{align}$ $

(4.7)

By the duplication formula of the Gamma function $ \Gamma\left({2z} \right) \, = \frac{2^{2z-1}}{\sqrt{\pi}} \, \Gamma\left({z} \right) \, \Gamma\left({z+\frac{1}{2}} \right) $, we have the following equalities for the Gamma functions that appear in (4.7)

$\begin{align} & \frac{\Gamma\left({n+s} \right)}{\Gamma\left({\frac{1}{2}+\frac{n+s}{2}} \right)} \, = \frac{2^{n+s-1}}{\sqrt{\pi}} \, \Gamma\left({\frac{n+s}{2}} \right), \end{align}$ $

(4.8)

$\begin{align} [0.2cm] & \frac{\Gamma\left({1+s} \right)}{\Gamma\left({\frac{1+s}{2}} \right)} \, = \frac{2^s}{\sqrt{\pi}} \, \Gamma\left({1+\frac{s}{2}} \right), \end{align}$ $

(4.9)

$\begin{align} [0.2cm] & \frac{\Gamma\left({-s} \right)}{\Gamma\left({\frac{1}{2}-\frac{s}{2}} \right)} \, = \frac{2^{-s-1}}{\sqrt{\pi}} \, \Gamma\left({-\frac{s}{2}} \right). \end{align}$ $

(4.10)

Taking into account Eqs (4.8)–(4.10), expression Eq (4.7) simplifies to

$\begin{align} & \mathcal{M}\left\{{r^n \, \mathcal{F}^{-1}\left\{{\widehat{\widetilde{u}}_1\left({\kappa, \mathbf{s}} \right) +\widehat{\widetilde{u}}_2\left({\kappa, \mathbf{s}} \right)\Big|_{p = -1} -\frac{d^2}{c^2} \, \widehat{\widetilde{u}}_3\left({\kappa, \mathbf{s}} \right)\Big|_{p = -1}}\right\}\left({r, \mathbf{s}}\right)}\right\}\left({\gamma-n+1, \mathbf{s}}\right) \\[0.2cm] & \quad = \left[{B_1^\ast\left({ \mathbf{s}} \right) +\frac{ \mathbf{s}}{c^2} \left[{B_2^\ast\left({ \mathbf{s}} \right) -d^2} \right]} \right] \, \frac{\left({B_2\left({ \mathbf{s}} \right) +B_1\left({ \mathbf{s}} \right)} \right)^{-\frac{s}{2}-1}}{\pi^{\frac{n}{2}}} \, 2^{s-1} \, \Gamma\left({\frac{n+s}{2}} \right) \, \Gamma\left({1+\frac{s}{2}} \right) \Bigg|_{s = \gamma-n+1} \end{align}$ $

and, consequently, the fractional moments of arbitrary order $ \gamma $ in the Laplace domain are given by

$\begin{align} \widetilde{\mathbf{M}}_{{n;\gamma}}^{{\alpha, \mu;\beta, \nu}}\left({ \mathbf{s}} \right) = \left[{B_1^\ast\left({ \mathbf{s}} \right) +\frac{ \mathbf{s}}{c^2} \left[{c^2 \, B_2^\ast\left({ \mathbf{s}} \right) -d^2} \right]} \right] \, \frac{\left({B_2\left({ \mathbf{s}} \right) +B_1\left({ \mathbf{s}} \right)} \right)^{\frac{-\gamma+n-3}{2}}}{\pi^{\frac{n}{2}}} \, 2^{\gamma-n} \, \Gamma\left({\frac{\gamma+1}{2}} \right) \, \Gamma\left({\frac{3+\gamma-n}{2}} \right). \end{align}$ $

(4.11)

If we restrict (4.11) to the time-fractional telegraph equation of distributed order with Caputo fractional derivatives, i.e., if we consider $ \mu = \nu = 1 $ (which implies that $ B_1^\ast\left({ \mathbf{s}} \right) = \mathbf{s}^{-1} B_1\left({ \mathbf{s}} \right) $ and $ B_2^\ast\left({ \mathbf{s}} \right) -\frac{d^2}{c^2} = \mathbf{s}^{-2}\left[{B_2\left({ \mathbf{s}} \right)-\frac{d^2}{c^2}} \right] $ by Remark 3.1), then (4.11) becomes equal to

$\begin{align} \widetilde{\mathbf{M}}_{{n;\gamma}}^{{\alpha, 1;\beta, 1}}\left({ \mathbf{s}} \right) \, = \frac{c^2 \, B_1\left({ \mathbf{s}} \right) +c^2 \, B_2\left({ \mathbf{s}} \right) -d^2}{\pi^{\frac{n}{2}} \, c^2 \, \mathbf{s}} \, \left({B_2\left({ \mathbf{s}} \right) +B_1\left({ \mathbf{s}} \right)} \right)^{\frac{-\gamma+n-3}{2}} \, 2^{\gamma-n} \, \Gamma\left({\frac{\gamma+1}{2}} \right) \, \Gamma\left({\frac{3+\gamma-n}{2}} \right), \end{align}$ $

which coincides with the correspondent expression deduced in ^[46]. Let us now analyse expression Eq (4.11) for some special cases:

● When $ \gamma = n-2k-3 $, with $ n > 2k+3 $ and $ k \in \mathbb{N}_0 $, the correspondent moments in the Laplace domain become infinite.

● When $ \gamma = 1 $ (mean value), we have

$\begin{align} \widetilde{\mathbf{M}}_{{n;1}}^{{\alpha, \mu;\beta, \nu}}\left({ \mathbf{s}} \right) \, = \left[{B_1^\ast\left({ \mathbf{s}} \right) +\frac{ \mathbf{s}}{c^2} \left[{c^2 \, B_2^\ast\left({ \mathbf{s}} \right) -d^2} \right]} \right] \, \frac{\left({B_2\left({ \mathbf{s}} \right) +B_1\left({ \mathbf{s}} \right)} \right)^{\frac{n}{2}-2}}{\pi^{\frac{n}{2}}} \, 2^{1-n} \, \Gamma\left({2-\frac{n}{2}} \right), \end{align}$ $

(4.12)

which becomes infinite when $ n = 4+2k $, with $ k \in \mathbb{N}_0 $.

● When $ \gamma = 2 $ (variance), we have

$\begin{align} \widetilde{\mathbf{M}}_{{n;2}}^{{\alpha, \mu;\beta, \nu}}\left({ \mathbf{s}} \right) = \left[{B_1^\ast\left({ \mathbf{s}} \right) +\frac{ \mathbf{s}}{c^2} \left[{c^2 \, B_2^\ast\left({ \mathbf{s}} \right) -d^2} \right]} \right] \, \frac{\left({B_2\left({ \mathbf{s}} \right) +B_1\left({ \mathbf{s}} \right)} \right)^{\frac{n-5}{2}}}{\pi^{\frac{n+1}{2}}} \, 2^{3-n} \, \Gamma\left({\frac{5-n}{2}} \right), \end{align}$ $

(4.13)

which becomes infinite when $ n = 5+2k, $ with $ k \in \mathbb{N}_0 $.

4.1. Tauberian analysis for the second-order moment (variance)

When the fundamental solution is a positive function, it is possible to classify the diffusion process by analysing the correspondent second-order moment, also called the mean squared displacement of a particle. This is obtained by comparison with the variance in the normal diffusion process. In this subsection we consider the particular case of double-order distributed fractional derivatives, and we analyze the second-order moment for short and long-time. We separate our analysis between the diffusion and the wave cases. The following Laplace inversion formulas will be needed in the sequel:

● Formula (2.1.1.1) in ^[63]

$\begin{align} & \mathcal{L}^{-1}\left\{{\frac{1}{ \mathbf{s}^\nu}}\right\}\left({t}\right) \, = \frac{t^{\nu-1}}{\Gamma\left({\nu} \right)}, \qquad \nu > 0. \end{align}$ $

(4.14)

● Formula (5.1.26) in ^[61]

$\begin{align} \mathcal{L}^{-1}\left\{{\frac{s^{\alpha\gamma-\beta}}{\left({s^\alpha-\lambda} \right)^\gamma}}\right\}\left({t}\right) \, = t^{\beta-1} \, E_{\alpha, \beta}^\gamma \left({\lambda t^\alpha} \right), \qquad \mathrm{Re}\left({\alpha} \right), \mathrm{Re}\left({\beta} \right) > 0, \; \; \lambda \in \mathbb{C}, \end{align}$ $

(4.15)

where $ E_{\alpha, \beta}^\gamma $ is the three parameter Mittag-Leffler function given by (2.14).

4.1.1. Two composite time-fractional derivatives in the diffusion case

Here we consider $ b_2\left({\beta, \nu} \right) \, = 0 $, which implies that $ B_2\left({ \mathbf{s}} \right) = B_2^\ast\left({ \mathbf{s}} \right) \, = 0 $. In this case, the second-order moment in the Laplace domain becomes

$\begin{align} \widetilde{\mathbf{M}}_{{n;2}}^{{\alpha, \mu;-, -}}\left({ \mathbf{s}} \right) = \widetilde{\mathbf{M}}_{{n;2}}^{{\alpha, \mu}}\left({ \mathbf{s}} \right) = \frac{2^{1-n} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}}} \, B_1^\ast\left({ \mathbf{s}} \right) \, \left({B_1\left({ \mathbf{s}} \right)} \right)^{\frac{n-5}{2}}, \quad n \neq 5+2k, \; k \in \mathbb{N}_0. \end{align}$ $

(4.16)

Further, we assume

$\begin{align} & b_1\left({\alpha, \mu} \right) \, = k_1 \, \delta\left({\alpha-\alpha_1} \right) \, \delta\left({\mu-\mu_1} \right) +k_2 \, \delta\left({\alpha-\alpha_2} \right) \, \delta\left({\mu-\mu_2} \right) \end{align}$ $

(4.17)

with $ 0 < \alpha_1 < \alpha_2 \leq 1 $, $ 0 \leq \mu_1, \mu_2 \leq 1, $ $ \mu_2 < \mu_1 \frac{1-\alpha_1}{1-\alpha_2} $, $ k_1, k_2 > 0 $, and $ k_1+k_2 = 1 $. For this $ b_1\left({\alpha, \mu} \right) $ we get

$\begin{align} & B_1\left({ \mathbf{s}} \right) \, = \frac{a k_1}{c^2} \, \mathbf{s}^{\alpha_1} +\frac{a k_2}{c^2} \, \mathbf{s}^{\alpha_2} \qquad \mbox{and} \qquad B_1^\ast\left({ \mathbf{s}} \right) \, = \frac{a k_1}{c^2} \, \mathbf{s}^{-\mu_1\left({1-\alpha_1} \right)} +\frac{a k_2}{c^2} \, \mathbf{s}^{-\mu_2\left({1-\alpha_2} \right)}. \end{align}$ $

(4.18)

Considering Eq (4.18) in Eq (4.16) we get

(4.19)

To invert the Laplace transform of $ \widetilde{\mathbf{M}}_{{n; 2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}} $ we first rearrange the expression Eq (4.19):

$\begin{align} \widetilde{\mathbf{M}}_{{n;2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({ \mathbf{s}} \right) & = \frac{2^{1-n} \, \left({a \, k_2} \right)^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, \frac{k_1}{k_2} \, \frac{ \mathbf{s}^{\frac{\left({\alpha_2-\alpha_1} \right)\left({5-n} \right)}{2} +\frac{\alpha_2\left({n-5} \right)}{2}-\mu_1\left({1-\alpha_1} \right)}}{\left({s^{\alpha_2-\alpha_1} -\left({-\frac{k_1}{k_2}} \right)} \right)^{\frac{5-n}{2}}} \\[0.2cm] & +\frac{2^{1-n} \, \left({a \, k_2} \right)^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, \frac{ \mathbf{s}^{\frac{\left({\alpha_2-\alpha_1} \right)\left({5-n} \right)}{2} +\frac{\alpha_2\left({n-5} \right)}{2}-\mu_2\left({1-\alpha_2} \right)}}{\left({s^{\alpha_2-\alpha_1} -\left({-\frac{k_1}{k_2}} \right)} \right)^{\frac{5-n}{2}}}. \end{align}$ $

(4.20)

Taking into account Eq (4.15) with

$\begin{align} & \alpha = \alpha_2-\alpha_1, \qquad \qquad \gamma = \frac{5-n}{2}, \qquad \qquad \lambda = -\frac{k_1}{k_2}, \\[0.2cm] & \beta = \frac{\alpha_2 \left({5-n} \right)}{2} +\mu_1\left({1-\alpha_1} \right) \; \; \text{(1st term)}, \qquad \beta = \frac{\alpha_2 \left({5-n} \right)}{2} +\mu_2\left({1-\alpha_2} \right) \; \; \text{(2nd term)}, \end{align}$ $

we get from Eq (4.20) that

$\begin{align} \mathbf{M}_{{n;2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right) & = \frac{2^{1-n} \, \left({a \, k_2} \right)^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, \frac{k_1}{k_2} \, t^{\frac{\alpha_2 \left({5-n} \right)}{2} +\mu_1\left({1-\alpha_1} \right)-1} \, E_{\alpha_2-\alpha_1, \, \frac{\alpha_2 \left({5-n} \right)}{2} +\mu_1\left({1-\alpha_1} \right)}^{\frac{5-n}{2}} \left({-\frac{k_1}{k_2} \, t^{\alpha_2-\alpha_1}} \right) \\[0.2cm] & \qquad +\frac{2^{1-n} \, \left({a \, k_2} \right)^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, t^{\frac{\alpha_2 \left({5-n} \right)}{2} +\mu_2\left({1-\alpha_2} \right)-1} \, E_{\alpha_2-\alpha_1, \, \frac{\alpha_2 \left({5-n} \right)}{2} +\mu_2\left({1-\alpha_2} \right)}^{\frac{5-n}{2}} \left({-\frac{k_1}{k_2} \, t^{\alpha_2-\alpha_1}} \right). \end{align}$ $

(4.21)

Remark 4.1. For $ n = 1, $ the expression Eq (4.21) reduces to the expression (28) in ^[51] with suitable identification of the parameters, which indicates consistency in our results.

The graphical representation of $ \mathbf{M}_{{n; 2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}} $ as a function of $ t $ using Eq (4.21) is not an easy procedure due to the presence of the three parameter Mittag-Leffler function $ E_{\alpha, \beta}^\gamma $. The numerical implementation of this special function is possible for some range of the parameter $ \alpha $ (see ^[64]), which do not include all the cases studied in this work. Therefore, we will make an asymptotic analysis of (4.19) using the Tauberian analysis. Since $ \mathbf{s}^{-\mu_2\left({1-\alpha_2} \right)+\mu_1\left({1-\alpha_1} \right)} \to 0 $ and $ \mathbf{s}^{\alpha_2-\alpha_1} \to 0 $ as $ \mathbf{s} \to 0 $ then, we get the following asymptotic behaviour of $ \widetilde{\mathbf{M}}_{{n; 2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({s} \right) $ as $ \mathbf{s} \to 0: $

$\begin{align} \widetilde{\mathbf{M}}_{{n;2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({ \mathbf{s}} \right) & = \frac{2^{1-n} \, a^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \left({k_1 \, \mathbf{s}^{-\mu_1\left({1-\alpha_1} \right)} +k_2 \, \mathbf{s}^{-\mu_2\left({1-\alpha_2} \right)}} \right) \left({k_1 \, \mathbf{s}^{\alpha_1} +k_2 \, \mathbf{s}^{\alpha_2}} \right)^{\frac{n-5}{2}} \\[0.2cm] & \sim \frac{2^{1-n} \, \left({a\, k_1} \right)^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, \mathbf{s}^{-\mu_1\left({1-\alpha_1} \right) +\frac{\alpha_1\left({n-5} \right)}{2}}. \end{align}$ $

(4.22)

Concerning the symbol $ \sim $ in the previous and subsequent expressions, we say that $ f $ and $ g $ are asymptotically equivalent as $ w \to \infty $ (resp. as $ w \to 0 $), i.e., $ f \sim g $, if and only if $ \lim_{w \to \infty} \frac{f\left({w} \right)}{g\left({w} \right)} = 1 $ (resp. $ \lim_{w \to 0} \frac{f\left({w} \right)}{g\left({w} \right)} = 1 $).

Using (4.14) to invert the Laplace transform in (4.22), we obtain the asymptotic behavior of $ \mathbf{M}_{{n; 2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}} $ for $ t \to +\infty, $ with $ 0 \leq \mu_1 \leq 1 $ and $ n $ and $ \alpha_1 $ according to the following cases:

$\begin{align} \mathbf{M}_{{n;2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right) \, \sim \begin{cases} \frac{2^{1-n} \, \left({a\, k_1} \right)^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, \frac{t^{\mu_1 +\frac{\alpha_1\left({5-n-2\mu_1} \right)}{2}-1}}{\Gamma\left({\mu_1 +\frac{\alpha_1\left({5-n-2\mu_1} \right)}{2}} \right)}, & \alpha_1 < \alpha_2, \; \; n = 1, 2, 3, 4 \\[0.6cm] \frac{2^{1-n} \, \left({a\, k_1} \right)^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, \frac{t^{\mu_1 +\frac{\alpha_1\left({5-n-2\mu_1} \right)}{2}-1}}{\Gamma\left({\mu_1 +\frac{\alpha_1\left({5-n-2\mu_1} \right)}{2}} \right)}, & \alpha_1 < \dfrac{2\mu_1}{2\mu_1+n-5} \wedge \alpha_1 < \alpha_2, \; n = 6, 8, \ldots \end{cases}. \end{align}$ $

(4.23)

To classify the type of diffusion process we need to compare $ \mathbf{M}_{{n; 2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}} $ with the moment of the normal diffusion process which is given by

$\begin{equation} \mathbf{M}_{{n;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}} = \frac{2^{1-n}(ak_1)^{\frac{n-3}{2}}}{\pi^{\frac{n-1}{2}} c^{n-3}}\, t^{\frac{3-n}{2}}. \end{equation}$ $

(4.24)

According with the dimension $ n $ we have the following cases:

● $ n = 1, 2, 3 $: $ \mathbf{M}_{{n; 2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right)/\mathbf{M}_{{n; 2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right) \to 0 $, as $ t \to +\infty, $ for all $ 0 \leq \mu_1 < 1, $ and all admissible $ \alpha_1 $ and $ n, $ which corresponds to a subdiffusion process in the long time. In the limit case, $ \mu_1 = 1 $ (Caputo case), for $ n = 1, 2 $ we still have a subdiffusion process while for $ n = 3 $ holds $ \mathbf{M}_{{3;2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right)/\mathbf{M}_{{3;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right) \to k > 0 $, as $ t \to +\infty, $ thus the process coincides with the normal diffusion in the long time;

● $ n = 4 $: The classification of the type of diffusion depends on the type $ \mu_1. $

▶ For $ 0\leq \mu_1 < 1/2 $ holds $ \mathbf{M}_{{4;2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right)/\mathbf{M}_{{4;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right) \to 0 $, as $ t \to +\infty, $ thus corresponding to a subdiffusion process in the long time;

▶ For $ \mu_1 = 1/2 $ holds $ \mathbf{M}_{{4;2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right)/\mathbf{M}_{{4;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right) \to k > 0 $, as $ t \to +\infty, $ thus the process coincides with the normal diffusion in the long time;

▶ For $ 1/2 < \mu_1 \leq 1 $ holds $ \mathbf{M}_{{4;2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right)/\mathbf{M}_{{4;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right) \to +\infty $, as $ t \to +\infty, $ thus corresponding to a superdiffusion process in the long time.

● $ n = 6+2k $: The moment $ \mathbf{M}_{{n; 2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right) $ is positive when $ n = 8+4k $ and negative when $ n = 6+4k, $ $ k \in \mathbb{Z}^+ $. This is due to the change of sign of the gamma function in the numerator. In the second case, a probabilistic interpretation is no longer possible.

Finally, we note a different behaviour of the monotonicity of the second-order moment along the dimensions, depending on the values assumed by the several parameters in the expression. When $ n = 1, 2, 3, 4 $, if we assume that $ c > 0 $, then the following conclusions about $ \mathbf{M}_{{n; 2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}} $ for large values of $ t $ can be drawn:

● $ n = 1 $: $ \mathbf{M}_{{n; 2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}} $ is an increasing function when $ \frac{1-\mu_1}{2-\mu_1} < \alpha_1 \leq 1 $, is constant when $ \alpha_1 = \frac{1-\mu_1}{2-\mu_1} $, and is a decreasing function when $ 0 < \alpha_1 < \frac{1-\mu_1}{2-\mu_1} \leq 0.5 $, with $ 0 \leq \mu_1 \leq 1 $.

● $ n = 2 $: $ \mathbf{M}_{{n; 2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}} $ is an increasing function when $ \frac{2-2\mu_1}{3-2\mu_1} < \alpha_1 \leq 1 $, is constant when $ \alpha_1 = \frac{2-2\mu_1}{3-2\mu_1} $, and is a decreasing function when $ 0 < \alpha_1 < \frac{2-2\mu_1}{3-2\mu_1} \leq \frac{2}{3} $, with $ 0 \leq \mu_1 \leq 1 $.

● $ n = 3 $: $ \mathbf{M}_{{n; 2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}} $ is a decreasing function when $ 0 < \alpha_1 < 1 $ and $ 0 \leq \mu_1 < 1, $ and is constant when $ \alpha_1 = 1 $ or $ 0 \leq \alpha_1 \leq 1 $ and $ \mu_1 = 1 $.

● $ n = 4 $: $ \mathbf{M}_{{n; 2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}} $ is a decreasing function for all $ 0 < \alpha_1 \leq 1 $ and $ 0 \leq \mu_1 < 1 $, and is constant when $ \alpha_1 = 0 $ and $ \mu_1 = 1 $.

Now, we study the asymptotic behaviour of $ \mathbf{M}_{{n; 2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}} $ for small values of $ t. $ From Eq (4.19) we have the following asymptotic behaviour when $ \mathbf{s} \to +\infty $:

$\begin{align} \widetilde{\mathbf{M}}_{{n;2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({ \mathbf{s}} \right) & = \frac{2^{1-n} \, a^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \left({k_1 \, \mathbf{s}^{-\mu_1\left({1-\alpha_1} \right)} +k_2 \, \mathbf{s}^{-\mu_2\left({1-\alpha_2} \right)}} \right) \left({k_2 \, \mathbf{s}^{\alpha_1} +k_2 \, \mathbf{s}^{\alpha_2}} \right)^{\frac{n-5}{2}} \\[0.2cm] & \sim \frac{2^{1-n} \, \left({a\, k_2} \right)^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, \mathbf{s}^{-\mu_2\left({1-\alpha_2} \right) +\frac{\alpha_2\left({n-5} \right)}{2}}. \end{align}$ $

(4.25)

Using Eq (4.14) to invert the Laplace transform in Eq (4.25), we obtain the asymptotic behavior of $ \mathbf{M}_{{n; 2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}} $ for $ t \to 0^+ $, with $ 0 \leq \mu_2 \leq 1 $ and $ n $ and $ \alpha_2 $ according to the following cases:

$\begin{align} \mathbf{M}_{{n;2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right) \, \sim \begin{cases} \frac{2^{1-n} \, \left({a\, k_2} \right)^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, \frac{t^{\mu_2 +\frac{\alpha_2\left({5-n-2\mu_2} \right)}{2}-1}}{\Gamma\left({\mu_2 +\frac{\alpha_2\left({5-n-2\mu_2} \right)}{2}} \right)}, & \alpha_2 > \alpha_1, \; \; n = 1, 2, 3, 4 \\[0.6cm] \frac{2^{1-n} \, \left({a\, k_2} \right)^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, \frac{t^{\mu_2 +\frac{\alpha_2\left({5-n-2\mu_2} \right)}{2}-1}}{\Gamma\left({\mu_2 +\frac{\alpha_2\left({5-n-2\mu_2} \right)}{2}} \right)}, & \alpha_2 < \dfrac{2\mu_2}{2\mu_2+n-5} \wedge \alpha_2 > \alpha_1, \; n = 6, 8, \ldots \end{cases}. \end{align}$ $

(4.26)

Comparing $ \mathbf{M}_{{n; 2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}} $ with $ \mathbf{M}_{{n; 2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}} $ when $ t \to 0^+ $, we have the following conclusions:

● $ n = 1, 2, 3 $: $ \mathbf{M}_{{n; 2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right)/\mathbf{M}_{{n; 2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right) \to +\infty $, as $ t \to 0^+ $, for all $ 0 \leq \mu_1 < 1, $ and all admissible $ \alpha_1 $ and $ n, $ which corresponds to a superdiffusion process in the short time. In the limit case, $ \mu_1 = 1 $ (Caputo case), for $ n = 1, 2 $ we still have a superdiffusion process while for $ n = 3 $ holds $ \mathbf{M}_{{3;2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right)/\mathbf{M}_{{3;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right) \to k > 0 $, as $ t \to +\infty, $ thus the process coincides with the normal diffusion in the short time;

● $ n = 4 $: The classification of the type of diffusion depends on the parameter $ \mu_1. $

▶ For $ 0\leq \mu_1 < 1/2 $ holds $ \mathbf{M}_{{4;2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right)/\mathbf{M}_{{4;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right) \to +\infty $, as $ t \to 0^+ $, thus corresponding to a superdiffusion process in the short time;

▶ For $ \mu_1 = 1/2 $ holds $ \mathbf{M}_{{4;2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right)/\mathbf{M}_{{4;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right) \to k > 0 $, as $ t \to 0^+ $, thus the process coincides with the normal diffusion in the short time;

▶ For $ 1/2 < \mu_1 \leq 1 $ holds $ \mathbf{M}_{{4;2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right)/\mathbf{M}_{{4;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right) \to 0 $, as $ t \to 0^+ $, thus corresponding to a subdiffusion process in the short time.

● $ n = 6+2k $: As happen in the long time case the moment is not always positive, and hence also here it is not possible to perform a probabilistic interpretation for all the values of $ n $.

4.1.2. Two composite time-fractional derivatives in the wave case

Here we consider $ b_1\left({\alpha, \mu} \right) \, = 0 $. Hence, $ B_1\left({ \mathbf{s}} \right) = \, B_1^\ast\left({ \mathbf{s}} \right) \, = 0 $ and the second-order moment in the Laplace domain becomes

$\begin{align} \mathbf{M}_{{n;2}}^{{-, -;\beta, \nu}}\left({ \mathbf{s}} \right) = \mathbf{M}_{{n;2}}^{{\beta, \nu}}\left({ \mathbf{s}} \right) = \frac{2^{1-n} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}}} \, \mathbf{s} \, B_2^\ast\left({ \mathbf{s}} \right) \, \left({B_2\left({ \mathbf{s}} \right)} \right)^{\frac{n-5}{2}}, \quad n \neq 5+2k, \, k \in \mathbb{N}_0. \end{align}$ $

(4.27)

Let us now assume that

$\begin{align} & b_2\left({\beta, \nu} \right) \, = k_1 \, \delta\left({\beta-\beta_1} \right) \, \delta\left({\nu-\nu_1} \right) +k_2 \, \delta\left({\beta-\beta_2} \right) \, \delta\left({\nu-\nu_2} \right) \end{align}$ $

with $ 1 < \beta_1 < \beta_2 \leq 2 $, $ 0 \leq \nu_1, \nu_2 \leq 1 $, $ \nu_2 < \nu_1 \frac{2-\beta_1}{2-\beta_2} $, $ k_1, k_2 > 0 $, and $ k_1+k_2 = 1 $. For this $ b_2\left({\beta, \nu} \right) $ we get

$\begin{align} & B_2\left({ \mathbf{s}} \right) \, = \frac{k_1}{c^2} \, \mathbf{s}^{\beta_1} +\frac{k_2}{c^2} \, \mathbf{s}^{\beta_2} \qquad \mbox{and} \qquad B_2^\ast\left({ \mathbf{s}} \right) \, = \frac{k_1}{c^2} \, \mathbf{s}^{-\nu_1\left({2-\beta_1} \right)} +\frac{k_2}{c^2} \, \mathbf{s}^{-\nu_2\left({2-\beta_2} \right)}. \end{align}$ $

(4.28)

Considering Eq (4.28) in Eq (4.27) we get

$\begin{align} &\widetilde{\mathbf{M}}_{{n;2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}}\left({ \mathbf{s}} \right) = \frac{2^{1-n} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, \mathbf{s} \left({k_1 \, \mathbf{s}^{-\nu_1\left({2-\beta_1} \right)} +k_2 \, \mathbf{s}^{-\nu_2\left({2-\beta_2} \right)}} \right) \left({k_1 \, \mathbf{s}^{\beta_1} +k_2 \, \mathbf{s}^{\beta_2}} \right)^{\frac{n-5}{2}}. \end{align}$ $

(4.29)

Inverting the Laplace transform of $ \widetilde{\mathbf{M}}_{{n; 2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}}\left({s} \right) $ following the same steps of the deduction of Eq (4.21) we get

$\begin{align} \mathbf{M}_{{n;2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}}\left({t} \right) & = \frac{2^{1-n} \, k_2^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, \frac{k_1}{k_2} \, t^{\frac{\beta_2 \left({5-n} \right)}{2} +\nu_1\left({2-\beta_1} \right)-2} \, E_{\beta_2-\beta_1, \, \frac{\beta_2 \left({5-n} \right)}{2} +\nu_1\left({2-\beta_1} \right)-1}^{\frac{5-n}{2}} \left({-\frac{k_1}{k_2} \, t^{\beta_2-\beta_1}} \right) \\[0.2cm] & \qquad +\frac{2^{1-n} \, k_2^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, t^{\frac{\beta_2 \left({5-n} \right)}{2} +\nu_2\left({2-\beta_2} \right)-2} \, E_{\beta_2-\beta_1, \, \frac{\beta_2 \left({5-n} \right)}{2} +\nu_2\left({2-\beta_2} \right)-1}^{\frac{5-n}{2}} \left({-\frac{k_1}{k_2} \, t^{\beta_2-\beta_1}} \right). \end{align}$ $

(4.30)

First, we study the asymptotic behaviour of $ \mathbf{M}_{{n; 2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}} $ for large values of $ t. $ From Eq (4.19) we have the following asymptotic behaviour when $ \mathbf{s} \to 0: $

$\begin{align} \widetilde{\mathbf{M}}_{{n;2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}}\left({ \mathbf{s}} \right) & = \frac{2^{1-n} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \mathbf{s} \left({k_1 \, \mathbf{s}^{-\nu_1\left({2-\beta_1} \right)} +k_2 \, \mathbf{s}^{-\nu_2\left({2-\beta_2} \right)}} \right) \left({k_1 \, \mathbf{s}^{\beta_1} +k_2 \, \mathbf{s}^{\beta_2}} \right)^{\frac{n-5}{2}} \\[0.2cm] & \sim \frac{2^{1-n} \, k_1^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, \mathbf{s}^{1-\nu_1\left({2-\beta_1} \right) +\frac{\beta_1\left({n-5} \right)}{2}}. \end{align}$ $

(4.31)

Using Eq (4.14) to invert the Laplace transform in Eq (4.31), we obtain the asymptotic behavior of $ \mathbf{M}_{{n; 2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}} $ for $ t \to + \infty, $ with $ \beta_1, $ $ \nu_1, $ and $ n $ according to the following cases:

$\begin{align} \mathbf{M}_{{n;2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}}\left({t} \right) \, \sim \begin{cases} \frac{2^{1-n} \, k_1^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, \frac{t^{2\nu_1 +\frac{\beta_1\left({5-n-2\nu_1} \right)}{2}-2}}{\Gamma\left({2\nu_1+\frac{\beta_1\left({5-n-2\nu_1} \right)}{2}-1} \right)}, & \beta_1 < \beta_2 , \; 0 \leq \nu_1 \leq 1, \; n = 1, 2, 3 \\[0.6cm] \frac{2^{1-n} \, k_1^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, \frac{t^{2\nu_1 +\frac{\beta_1\left({5-n-2\nu_1} \right)}{2}-2}}{\Gamma\left({2\nu_1 +\frac{\beta_1\left({5-n-2\nu_1} \right)}{2}-1} \right)}, & \beta_1 < \beta_2 , \; \frac{1}{2} < \nu_1 \leq 1, \; n = 4 \end{cases}. \end{align}$ $

(4.32)

To classify the type of diffusion-wave process we need to compare $ \mathbf{M}_{{n; 2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}} $ with the normal diffusion process. The situation here depends on the dimension and we have the following cases:

● $ n = 1 $: $ \mathbf{M}_{{1;2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}}\left({t} \right)/ \mathbf{M}_{{1;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}(t) \to +\infty $, as $ t \to +\infty, $ for $ 1 < \frac{3-2\nu_1}{2-\nu_1} < \beta_1 < 2 $ and $ 0\leq \nu_1\leq 1, $ which corresponds to a superdiffusion process in the long time and $ \mathbf{M}_{{1;2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}}\left({t} \right)/ \mathbf{M}_{{1;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}} \to 0 $, as $ t \to +\infty, $ for $ 1 < \beta_1 < \frac{3-2\nu_1}{2-\nu_1} < 2 $ and $ 0\leq \nu_1\leq 1, $ which corresponds to a subdiffusion process in the long time. In the special case $ \beta_1 = \frac{3-2\nu_1}{2-\nu_1} $ the process coincides with the normal diffusion in the long time.

● $ n = 2 $: $ \mathbf{M}_{{n; 2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}}\left({t} \right)/ \mathbf{M}_{{2;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}(t) \to +\infty $, as $ t \to +\infty, $ for $ 1 < \frac{5-4\nu_1}{3-2\nu_1} < \beta_1 < 2 $ and $ 0\leq \nu_1\leq 1, $ which corresponds to a superdiffusion process in the long time and $ \mathbf{M}_{{n; 2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}}\left({t} \right)/ \mathbf{M}_{{2;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}(t) \to 0 $, as $ t \to +\infty, $ for $ 1 < \beta_1 < \frac{5-4\nu_1}{3-2\nu_1} < 2 $ and $ 0\leq \nu_1\leq 1, $ which corresponds to a subdiffusion process in the long time. In the special case $ \beta_1 = \frac{5-4\nu_1}{3-2\nu_1} $ the process coincides with the normal diffusion in the long time.

● $ n = 3 $ $ \mathbf{M}_{{3;2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}}\left({t} \right)/ \mathbf{M}_{{3;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}(t) \to 0 $, as $ t \to +\infty, $ for all $ 1 < \beta_1\leq 2 $ and $ 0 \leq \nu_1 < 1 $, thus corresponding to a subdiffusion process. For $ \nu_1 = 1 $ the process coincides with the normal diffusion case.

● $ n = 4 $: $ \mathbf{M}_{{4;2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}}\left({t} \right)/ \mathbf{M}_{{4;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}(t) \to 0 $, as $ t \to +\infty, $ for all $ 1 < \beta_1\leq 2 $ and $ 1/2 < \nu_1 \leq 1 $, thus corresponding to a subdiffusion process.

Finally, we study the asymptotic behaviour of $ \mathbf{M}_{{n; 2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}} $ for small values of $ t $ knowing the asymptotic behaviour of Eq (4.29) when $ \mathbf{s} \to +\infty. $ From (4.29), as $ \mathbf{s} \to +\infty, $ we have

$\begin{align} \widetilde{\mathbf{M}}_{{n;2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}}\left({ \mathbf{s}} \right) & = \frac{2^{1-n} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, \mathbf{s} \left({k_2 \, \mathbf{s}^{-\nu_1\left({2-\beta_1} \right)} +k_2 \, \mathbf{s}^{-\nu_2\left({2-\beta_2} \right)}} \right) \left({k_1 \, \mathbf{s}^{\beta_1} +k_2 \, \mathbf{s}^{\beta_2}} \right)^{\frac{n-5}{2}} \\[0.2cm] & \sim \frac{2^{1-n} \, k_1^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, \mathbf{s}^{1-\nu_2\left({2-\beta_2} \right) +\frac{\beta_2\left({n-5} \right)}{2}}. \end{align}$ $

(4.33)

Using Eq (4.14) to invert the Laplace transform in Eq (4.33), we obtain the asymptotic behavior of $ \mathbf{M}_{{n; 2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}} $ for $ t \to 0^+ $, with $ \beta_2, $ $ \nu_2, $ and $ n $ according to the following cases:

$\begin{align} \mathbf{M}_{{n;2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}}\left({t} \right) \, \sim \begin{cases} \frac{2^{1-n} \, k_2^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, \frac{t^{2\nu_2 +\frac{\beta_2\left({5-n-2\nu_2} \right)}{2}-2}}{\Gamma\left({2\nu_2+\frac{\beta_2\left({5-n-2\nu_2} \right)}{2}-1} \right)}, & \beta_2 > \beta_1, \; 0 \leq \nu_2 \leq 1, \; n = 1, 2, 3 \\[0.6cm] \frac{2^{1-n} \, k_2^{\frac{n-3}{2}} \, \Gamma\left({\frac{5-n}{2}} \right)}{\pi^{\frac{n-1}{2}} \, c^{n-3}} \, \frac{t^{2\nu_2 +\frac{\beta_2\left({5-n-2\nu_2} \right)}{2}-2}}{\Gamma\left({2\nu_2 +\frac{\beta_2\left({5-n-2\nu_2} \right)}{2}-1} \right)}, & \beta_2 > \beta_1 , \; \frac{1}{2} < \nu_2 \leq 1, \; n = 4 \end{cases}. \end{align}$ $

(4.34)

The analysis of Eq (4.34) is similar to the one performed for Eq (4.32). Regarding the classification of the diffusion-wave process the following conclusions can be taken:

● $ n = 1 $: $ \mathbf{M}_{{1;2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}}\left({t} \right)/ \mathbf{M}_{{1;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}(t) \to 0 $, as $ t \to 0^+ $, for $ 1 < \frac{3-2\nu_1}{2-\nu_1} < \beta_2 < 2 $ and $ 0\leq \nu_2 \leq 1 $, while $ \mathbf{M}_{{n; 2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}}\left({t} \right)/ \mathbf{M}_{{1;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}(t) \to +\infty $, as $ t \to 0^+ $, for $ 1 < \beta_2 < \frac{3-2\nu_1}{2-\nu_1} < 2 $ and $ 0\leq \nu_2 \leq 1. $ Hence, in the short time, the process is subdiffusive in the first case and is superdiffusive in the second case. In the special case $ \beta_1 = \frac{3-2\nu_1}{2-\nu_1} $ the process coincides with the normal diffusion in the short time.

● $ n = 2 $: $ \mathbf{M}_{{2;2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}}\left({t} \right)/ \mathbf{M}_{{2;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}(t) \to 0 $, as $ t \to 0^+ $, for $ 1 < \frac{5-4\nu_1}{3-2\nu_1} < \beta_2 < 2 $ and $ 0\leq \nu_2 \leq 1, $ which corresponds to a subdiffusion process in the short time, and $ \mathbf{M}_{{2;2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}}\left({t} \right)/ \mathbf{M}_{{2;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}(t) \to +\infty $, as $ t \to 0^+ $, for $ 1 < \beta_2 < \frac{5-4\nu_1}{3-2\nu_1} < 2 $ and $ 0\leq \nu_2 \leq 1, $ thus corresponding to a superdiffusion process in the short time. In the special case $ \beta_1 = \frac{5-4\nu_1}{3-2\nu_1} $ the process coincides with the normal diffusion in the short time.

● $ n = 3 $: $ \mathbf{M}_{{3;2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}}\left({t} \right)/ \mathbf{M}_{{3;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}(t) \to +\infty $, as $ t \to 0^+ $, for all $ 1 < \beta_2\leq 2 $ and $ 0 \leq \nu_2 < 1 $, thus corresponding to a superdiffusion process. For $ \nu_2 = 1 $ the process coincides with the normal diffusion case.

● $ n = 4 $: $ \mathbf{M}_{{4;2}}^{{\left({\beta_1, \beta_2} \right), \left({\nu_1, \nu_2} \right)}}\left({t} \right)/ \mathbf{M}_{{4;2}}^{{\left({1, 1} \right), \left({\mu_1, \mu_2} \right)}}(t) \to + \infty $, as $ t \to 0^+ $, for all $ 1 < \beta_2\leq 2 $ and $ 1/2 < \nu_2 \leq 1 $, thus corresponding to a superdiffusion process in the short time.

Remark 4.2. If we consider the Caputo case in Sections 4.1.1 and 4.1.2, our analysis of the diffusion-wave process for the double-order case improve the results presented in ^[46]. Moreover, considering single order derivatives and the one-dimensional case, it was proved in ^[65] that the fundamental solution corresponds to a probability density function only when the fractional derivatives are in the Caputo sense.

4.1.3. Graphical representations of the second-order moment for the long time

In this section we present and analyse the plots of the asymptotic behaviour of $ \mathbf{M}_{{n; 2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right) $, when $ t \to +\infty $, for some of the cases studied previously separating the diffusion and the wave cases. The plots were generated using Mathematica software and the commands available in it.

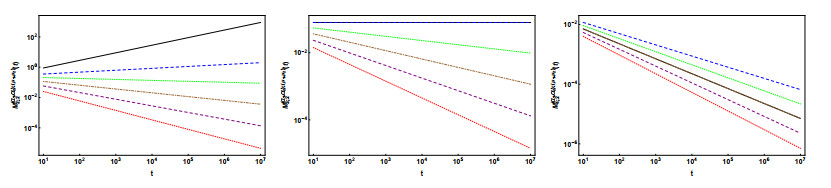
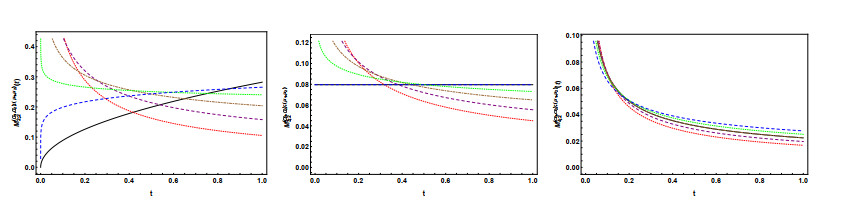
The diffusion case: In the following figures, we show the graphical representation of Eq (4.23) for $ n = 1, 2, 3, 4 $, $ \alpha_1 = 0.25, 0.50, 0.75 $, and different values $ \mu_1, $ using a logarithmic scale in the axes when needed.

Looking at the plots we see that the classification of the diffusion process in each dimension agrees with the analysis of Eq (4.23) performed previously. The plots show an interpolation between the extreme cases $ \mu_1 = 0 $ and $ \mu_1 = 1, $ which correspond to the Riemann-Liouville (RL) and Caputo cases, respectively. The extreme cases have different behaviour, e.g., the slope of the variance is different and in the dimension, $ n = 3 $ the variance is constant in the Caputo case. In contrast, in the RL case, the variance decreases for large values of $ t. $ Moreover, for $ \alpha_1 = 0.25 $ we can observe a different behaviour of the diffusion in dimensions $ n = 1 $ and $ n = 2: $ in the RL case the variance decreases for large values of $ t $ while in the Caputo case the variance increases.

Figure 1. Plots of the asymptotic behaviour of $ \mathbf{M}_{{1;2}}^{{\left({\alpha_1,\alpha_2} \right),\left({\mu_1,\mu_2} \right)}}\left({t} \right) $ when $ t \to +\infty $ for $ \alpha_1=0.25, 0.50, 0.75 $ (from left).

DownLoad: Full-Size Img PowerPoint

Figure 2. Plots of the asymptotic behaviour of $ \mathbf{M}_{{n;2}}^{{\left({\alpha_1,\alpha_2} \right),\left({\mu_1,\mu_2} \right)}}\left({t} \right) $ when $ t \to +\infty $ for $ n=2 $ and $ \alpha _1=0.25 $, $ n=3 $ and $ \alpha_1=0.50 $, $ n=4 $ and $ \alpha_1=0.75 $ (from left).

DownLoad: Full-Size Img PowerPoint

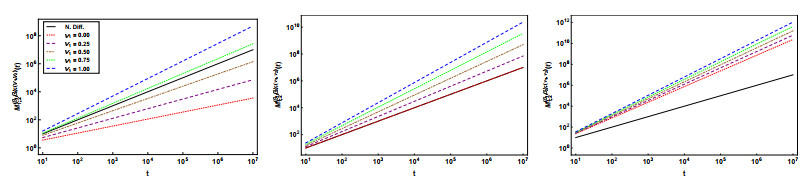
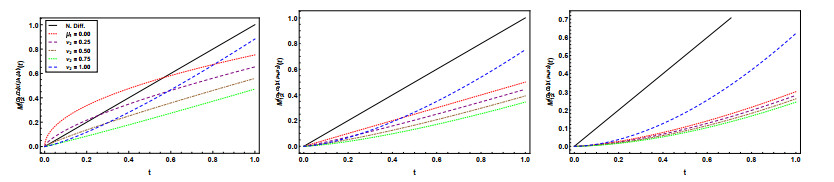
The wave case: In the following figures, we show the graphical representation of Eq (4.32) for $ n = 1, 2, 3, 4 $, $ \beta_1 = 1.25, 1.50, 1.75 $ and different values $ \nu_1 $.

For each dimension and different values of the fractional parameters, the process classification agrees with the analysis of Eq (4.32). The range of the plots increases with the increase of $ \beta_1 $ and $ \nu_1 $. Again it is interesting to observe the different behaviour of the variance for the extreme cases $ \nu_1 = 0 $ (RL case) and $ \nu_1 = 1 $ (Caputo case) for the dimension $ n = 3. $ Also the slope of the variance is different in the other dimensions.

Figure 3. Plots of the asymptotic behaviour of $ \mathbf{M}_{{1;2}}^{{\left({\beta_1,\beta_2} \right),\left({\nu_1,\nu_2} \right)}}\left({t} \right) $ when $ t \to +\infty $ for $ \beta_1=1.25, 1.50, 1.75 $ (from left).

DownLoad: Full-Size Img PowerPoint

Figure 4. Plots of the asymptotic behaviour of $ \mathbf{M}_{{n;2}}^{{\left({\beta_1,\beta_2} \right),\left({\nu_1,\nu_2} \right)}}\left({t} \right) $ when $ t \to +\infty $ for $ n=2 $ and $ \beta_1=1.25 $, $ n=3 $ and $ \beta_1=1.50 $, $ n=4 $ and $ \beta_1=1.75 $ (from left).

DownLoad: Full-Size Img PowerPoint

4.1.4. Graphical representations of the second-order moment for the short time

In this section we present and analyse the graphical representation of the asymptotic behaviour of $ \mathbf{M}_{{n; 2}}^{{\left({\alpha_1, \alpha_2} \right), \left({\mu_1, \mu_2} \right)}}\left({t} \right) $, when $ t \to 0^+ $, for some of the cases studied previously separating the diffusion and the wave cases. The plots were generated using Mathematica software and the commands available in it.

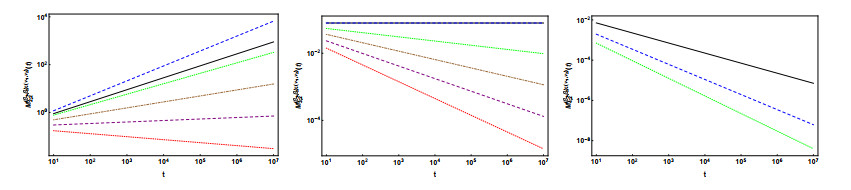
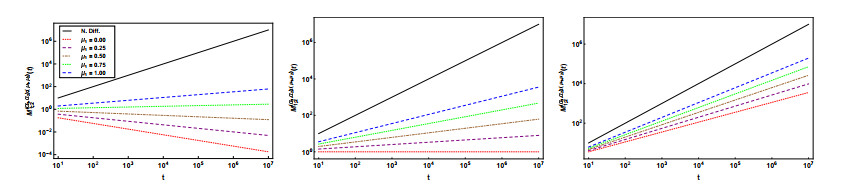
The diffusion case: In the following figures, we show the graphical representation of (4.26) for $ n = 1, 2, 3, 4 $, $ \alpha_2 = 0.25, 0.50, 0.75 $, and different values $ \mu_2. $

Looking at the plots we see that the range of the plots decreases with the increase of $ \alpha_2 $ and $ \mu_2 $. The type of process is in accordance with the conclusion made in the analysis of Eq (4.26). Again, we can observe a different behaviour of the variance for small values of $ t $ in the extreme cases $ \nu_2 = 0 $ and $ \nu_2 = 1, $ corresponding to the RL and Caputo cases, respectively. For $ \alpha_1 = 0.25 $ and the dimensions $ n = 1 $ and $ n = 2 $ the variance decreases in the RL case and increases in the Caputo case, for small values of $ t. $ In the case $ \nu_2 = 1 $ the plots coincide with the correspondent ones obtained in ^[46].

Figure 5. Plots of the asymptotic behaviour of $ \mathbf{M}_{{1;2}}^{{\left({\alpha_1,\alpha_2} \right),\left({\mu_1,\mu_2} \right)}}\left({t} \right) $ when $ t \to 0^+ $ for $ \alpha_2=0.25, 0.50, 0.75 $ (from left).

DownLoad: Full-Size Img PowerPoint

Figure 6. Plots of the asymptotic behaviour of $ \mathbf{M}_{{n;2}}^{{\left({\alpha_1,\alpha_2} \right),\left({\mu_1,\mu_2} \right)}}\left({t} \right) $ when $ t \to 0^+ $ for $ n=2 $ and $ \alpha_2=0.25 $, $ n=3 $ and $ \alpha_2=0.50 $, $ n=4 $ and $ \alpha_2=0.75 $ (from left).

DownLoad: Full-Size Img PowerPoint

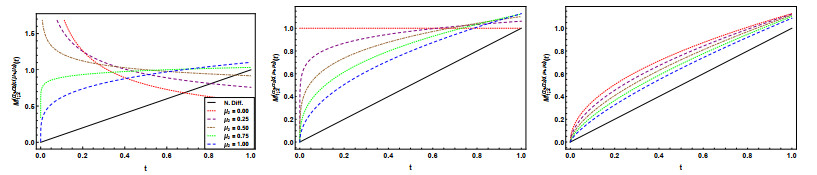
The wave case: In the following figures, we have the graphical representation of Eq (4.34) for $ n = 1, 2, 3, 4 $, $ \beta_2 = 1.25, 1.50, 1.75 $, and different values $ \nu_2 $ and $ n. $

Looking at the plots we see that the conclusions are similar to those already exposed. The behaviour of the functions is in accordance with the conclusions made in the analysis of (4.34). When $ \nu_2 = 1 $ the plots coincide with those presented in ^[46].

Figure 7. Plots of the asymptotic behaviour of $ \mathbf{M}_{{1;2}}^{{\left({\alpha_1,\alpha_2} \right),\left({\mu_1,\mu_2} \right)}}\left({t} \right) $ when $ t \to 0^+ $ for $ \beta_2=1.25, 1.50, 1.75 $ (from left).

DownLoad: Full-Size Img PowerPoint

Figure 8. Plots of the asymptotic behaviour of $ \mathbf{M}_{{n;2}}^{{\left({\alpha_1,\alpha_2} \right),\left({\mu_1,\mu_2} \right)}}\left({t} \right) $ when $ t \to 0^+ $ for $ n=2 $ and $ \beta_2=1.25 $, $ n=3 $ and $ \beta_2=0.50 $, $ n=4 $ and $ \beta_2=0.75 $ (from left).

DownLoad: Full-Size Img PowerPoint

5. Conclusions

The results presented here generalize those obtained in ^[46] by the introduction of the Hilfer derivative, that allows a smooth interpolation between the Riemann-Liouvile and the Caputo fractional derivatives. The solution of the Cauchy problem associated with the telegraph equation was expressed as convolutions with functions that are expressed by Laplace integrals involving Fox H-functions. For particular cases of the equation the solution can be simplified and we showed that we can recover known results presented in the literature, which reveals consistency of our results. The classification of the diffusion-wave process depends, not only on the spatial dimension, but also on the order and type of the derivatives. This is very different from previous works on the literature since in most cases the telegraph equation is studied only for Caputo or Riemann-Liouville fractional derivatives. It would be interesting to consider other types of density functions in addition to those considered in this article, but the calculations would become cumbersome.

Acknowledgments

The work of the authors was supported by Portuguese funds through CIDMA–Center for Research and Development in Mathematics and Applications, and FCT–Fundação para a Ciência e a Tecnologia, within projects UIDB/04106/2020 and UIDP/04106/2020.

N. Vieira was also supported by FCT via the 2018 FCT program of Stimulus of Scientific Employment - Individual Support (Ref: CEECIND/01131/2018).

The authors thank the anonymous reviewers for the careful reading of the manuscript, their suggestions, and additional references that have improved the article.

Conflict of interest

The authors declare there is no conflicts of interest.

References

[1]	Ruggiero M (2017) Alzheimer DNA vaccine and relativistic time dilation. J Neurol Stroke 7: 1–2.
[2]	Ruggiero M (2017) A Novel method to enhance immune responses Induced by HIV DNA vaccination. BAOJ HIV 3: 1–5.
[3]	Ruggiero M (2017) The Human Microbiota and the Immune System; Reflections on Immortality. Madridge J Immunol 1: 18–22.
[4]	Ruggiero M (2017) Is Rerum^Ò the new Coley's vaccine? Am J Immunol 13: 91–98. doi: 10.3844/ajisp.2017.91.98
[5]	Barthe L, Woodley JM, Przybylski C, et al. (2004) In vitro Intestinal Degradation and Absorption of Chondroitin Sulfate, a Glycosaminoglycan Drug. Arzneim-Forsch 54: 286–292.
[6]	Liu F, Zhang N, Li Z, et al. (2017) Chondroitin sulfate disaccharides modified the structure and function of the murine gut microbiome under healthy and stressed conditions. Sci Rep 7: 6783. doi: 10.1038/s41598-017-05860-6
[7]	Pacini S, Ruggiero M (2017) Description of a Novel Probiotic Concept: Implications for the Modulation of the Immune System. Am J Immunol 13: 107–113. doi: 10.3844/ajisp.2017.107.113
[8]	Vannucchi S, Pasquali F, Porciatti F, et al. (1988) Binding, internalization and degradation of heparin and heparin fragments by cultured endothelial cells. Thromb Res 49: 373–383. doi: 10.1016/0049-3848(88)90240-X
[9]	Longstaff C, Hogwood J, Gray E, et al. (2016) Neutralisation of the anti-coagulant effects of heparin by histones in blood plasma and purified systems. Thromb Haemostasis 115: 591–599. doi: 10.1160/th15-03-0214
[10]	Jeon KJ, Katsuraya K, Kaneko Y, et al. (1998) Studies on ionic interactions between a glycosaminoglycan chondroitin-6-sulfate and lysine-containing polypeptides by NMR spectroscopy. Polym J 30: 106–112. doi: 10.1295/polymj.30.106
[11]	Yang SS, Zhang R, Wang G, et al. (2017) The development prospection of HDAC inhibitors as a potential therapeutic direction in Alzheimer's disease. Transl Neurodegener 10: 19.
[12]	Chan PS, Caron JP, Rosa GJM, et al. (2005) Glucosamine and chondroitin sulfate regulate gene expression and synthesis of nitric oxide and prostaglandin E(2) in articular cartilage explants. Osteoarthritis Cartilage 13: 387–394. doi: 10.1016/j.joca.2005.01.003
[13]	Wang CT, Lin YT, Chiang BL, et al. (2006) High molecular weight hyaluronic acid down-regulates the gene expression of osteoarthritis-associated cytokines and enzymes in fibroblast-like synoviocytes from patients with early osteoarthritis. Osteoarthritis Cartilage 14: 1237–1247. doi: 10.1016/j.joca.2006.05.009
[14]	Hameroff SR, Craddock TJ, Tuszynski JA (2014) Quantum effects in the understanding of consciousness. J Syst Integr Neurosci 13: 229–252. doi: 10.1142/S0219635214400093
[15]	Karafyllidis IG (2017) Quantum transport in the FMO photosynthetic light-harvesting complex. J Biol Phys 43: 239–245. doi: 10.1007/s10867-017-9449-4
[16]	Pauls JA, Zhang Y, Berman GP, et al. (2012) Quantum coherence and entanglement in the avian compass. Phys Rev E Stat Nonlinear Soft Matter Phys 87: 062704.
[17]	Rieper E, Anders J, Vedral V (2011) Quantum entanglement between the electron clouds of nucleic acids in DNA. Physics.
[18]	Ruggiero M, Aterini S (2015) Electromagnetic fields. Encycl Cancer 15: 206–210.
[19]	Hameroff S, Penrose R (2014) Consciousness in the universe: A review of the "Orch OR" theory. Phys Life Rev 11: 39–78. doi: 10.1016/j.plrev.2013.08.002
[20]	Ruggiero M, Fiore MG, Magherini S, et al. (2013) Transcranial sonography in the diagnosis, follow-up and treatment of Myalgic Encephalomyelitis/Chronic Fatigue Syndrome. J IiME 7: 23–28.
[21]	Hameroff S, Trakas M, Duffield C, et al. (2013) Transcranial ultrasound (TUS) effects on mental states: A pilot study. Brain Stimul 6: 409–415. doi: 10.1016/j.brs.2012.05.002
[22]	Challacombe JF, Snow DM, Letourneau PC (1996) Actin filament bundles are required for microtubule reorientation during growth cone turning to avoid an inhibitory guidance cue. J Cell Sci 109: 2031–2040.
[23]	Wloga D, Joachimiak E, Fabczak H (2017) Tubulin Post-Translational Modifications and Microtubule Dynamics. Int J Mol Sci 18: E2207. doi: 10.3390/ijms18102207

This article has been cited by:

1.	Ravshan Ashurov, Rajapboy Saparbayev, Time-dependent identification problem for a fractional Telegraph equation with the Caputo derivative, 2024, 27, 1311-0454, 652, 10.1007/s13540-024-00240-0
2.	Mohammad Hossein Derakhshan, Stability analysis of difference-Legendre spectral method for two-dimensional Riesz space distributed-order diffusion-wave model, 2023, 144, 08981221, 150, 10.1016/j.camwa.2023.05.035

Reader Comments

Your name:*

Email:*
© 2018 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Molecular Science

1.1

Metrics

Article views(7930) PDF downloads(1231) Cited by(0)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

AIMS Molecular Science

On the impact of quantum biology and relativistic time dilation in autism

Related Papers:

Abstract

1. Introduction

2. Preliminaries

3. Generalized time-fractional telegraph equation of distributed order

3.1. Solution in the Fourier-Laplace domain

3.2. Solution in the space-time domain

3.3. Main result and corollary

4. Fractional moments

4.1. Tauberian analysis for the second-order moment (variance)

4.1.1. Two composite time-fractional derivatives in the diffusion case

4.1.2. Two composite time-fractional derivatives in the wave case

4.1.3. Graphical representations of the second-order moment for the long time

4.1.4. Graphical representations of the second-order moment for the short time

5. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Other Articles By Authors

Catalog

AIMS Molecular Science

On the impact of quantum biology and relativistic time dilation in autism

Related Papers:

Abstract

1. Introduction

2. Preliminaries

3. Generalized time-fractional telegraph equation of distributed order

3.1. Solution in the Fourier-Laplace domain

3.2. Solution in the space-time domain

3.3. Main result and corollary

4. Fractional moments

4.1. Tauberian analysis for the second-order moment (variance)

4.1.1. Two composite time-fractional derivatives in the diffusion case

4.1.2. Two composite time-fractional derivatives in the wave case

4.1.3. Graphical representations of the second-order moment for the long time

4.1.4. Graphical representations of the second-order moment for the short time

5. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog