1. Introduction
The theory of microarrays methodology was first introduced and demonstrated by Chang TW in 1983, for antibody microarrays in a scientific publicationand registered a series of patents [1].In 1990s, Microarrays were developed as a consequence of the efforts to speed up the process of drug discovery [2]. Traditional drug discovery was shaped for developing a number of candidate drugs and trying them one by one against diseases of interest. The long and limited method of trial and error based centered drug discovery could not be very effective for some perticular diseases. A group of researchers at affymax established a photolithography system to achieve this in a fashion similar to the synthesis of VLSI (Very Large Scale Integration) chips in the semiconductor industry [3]. The first version developed by the sister company Affymetrix came to be known as the Gene chip [4,5,6]. The "gene chip" industry started to grow significantly after the 1995 with the publication of Science Paper by the Ron Davis and Pat Brown labs at Stanford University. Simultaneously researchers at the Pat Brown's lab of Stanford University developed a different type of microarray [7]. With the establishment of companies such as Affymetrix, Agilent, Applied Microarrays, Arrayit, Illumina, and others. The technology of DNA microarrays has become the most sophisticated and the most widely used, while the use of protein, peptide and carbohydrate microarrays is expanding [8].
In the past few years, multivariate statistics for microarray data analysis has been the subject of thousands of research publications in Statistics, Bioinformatics, Machine learning, and Computational biology. Most of the traditional issues of multivariate statistics have been studied in the context of high-dimensional microarray data. The main types of data analysis needed for biomedical applications include [9,10]:
· Gene Selection: the procedure of feature selection, that finds the genes, strongly associated with a particular class.
· Classification: classifying diseases or predicting outcomes based on gene expression patterns, and perhaps even identifying the best treatment for given genetic signature [10].
· Clustering: finding new biological classes or refining existing ones [11].
Clustering can be used to find groups of similarly expressed genes in the aspiration of finding that both have a similar function [12]. On the other hand, another topic of interest is the classification of the microarray data for prediction of disease such as cancer using gene expression levels [13]. Classification of gene expression data samples involves dimension reduction and classifier design. Thus, in order to analyze gene expression profiles correctly, dimension reduction is an important process for the classification [14]. The goal of microarray data classification of cancer is to build an efficient and effective model that can differentiate the gene expressions of samples, i.e. classify tissue samples into different classes of the tumor. Nearest neighbor classification, Artificial Neural Network, Bayesian, Decision tree, Random forest methods and Support Vector Machine (SVM), are the most well-known approaches for classification. An overview of the methods mentioned above can be found in Lee et.al. [15].
Recently, many gene expression data classification and dimension reduction techniques have been introduced. You W et al. applied feature selection and feature extraction for dimension reduction of microarray by using Partial Least Squares (PLS) based information [16]. Xi M et al. used a binary quantum-behaved Particle Swarm Optimization and Support Vector Machine for feature selection and classification [17]. Wang et al. proposed a new tumor classification approach based on an ensemble of Probabilistic Neural Networks (PNN) and neighborhood rough set models based on gene selection [18]. Shen et al. proposed a modified particle swarm optimization that allows for the simultaneous selection of genes and samples [19]. Xie et al. developed a diagnosis model based on IFSFFS (Improved F-score and Sequential Forward Floating Search) with support vector machines (SVM) for diagnosis of erythema to squamous diseases [20]. Li et al. proposed an algorithm with a locally linear discriminant embedded in it, to map the microarray data to a low dimensional space, while Huang et al. recommended an upgraded decision forest method for the classification of microarray data that used a built-in feature selection method for fine-tuning [21,22].
In subsequent years, the use of gene expression profiles for cancer diagnoses has been the major focus in many microarray studies. Various gene selection methods and classification algorithms are proposed in the literature which are able to reduce the dimensionality by removing irrelevant, redundant and noisy genes for accurate classification of cancer [23].
2. Microarray Gene Expression Data Analysis Challenges
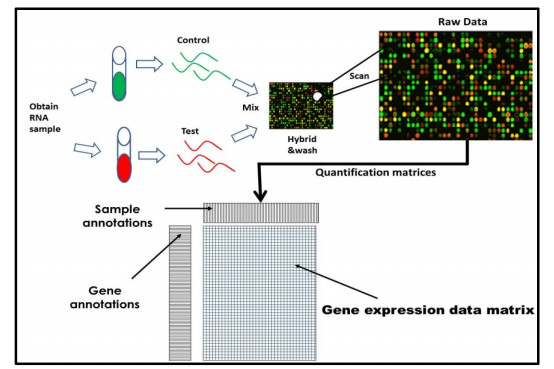
Microarray technology provided biologists with the ability to measure the expression levels of thousands of genes in a single experiment. The data from microarray consists of a small sample size and high dimensional data. A characteristic of gene expression microarray data is that the number of variables (genes) m far exceeds the number of samples n, commonly known as "curse of dimensionality" problem. Processing of microarray gene expression data is shown in Figure 1. To avoid the problem of the "curse of dimensionality", dimension reduction plays a crucial role in DNA microarray analysis. Microarray experiments provide huge amount of data to the scientific community, without appropriate methodologies and tools, significant information and knowledge hidden in these data may not be discovered. The vast amount of raw gene expression data leads to statistical and analytical challenges [24]. The challenge experienced by statisticians is the nature of the microarray data. The best statistical model will largely depend on the total number of possible gene combinations. Therefore, the impact of microarray technology on biology will depend heavily on data mining and statistical analysis. Conventional statistical methods give improper result due to high dimension of microarray data with limited number of patterns. Therefore, there is a need for methods capable of handling and exploring large data sets. The field of data mining and machine learning provides a wealth of methodologies and tools for analyzing large data sets. A sophisticated data-mining and analytical tool is required to correlate all of the data obtained from the arrays and which can help to group them in a meaningful way [25].
Data mining with machine learning is a process to discover meaningful, non-trivial, and potentially useful knowledge (patterns, relationships, trends, rules, anomalies, dependencies) from the large amount of data by using different types of automatic or semi-automatic techniques. Compared with classical statistical approaches, data mining is feasibly best seen as a process that incorporates a wider range of integrated methodologies and tools, including databases, machine learning, knowledge-based techniques, network technology, modeling, algorithms, and uncertainty handling [26].
Gene expression data of DNA microarray which represent the state of a cell at a molecular level, have a great prospective as a medical diagnosis tool [27]. Typical microarray data mining analysis include discriminant analysis, regression, clustering, association and deviation detection. Several machine learning techniques such as, Support Vector Machines (SVM) [28], k-Nearest Neighbours (kNN) [29], Artificial Neural Networks (ANN) [30], Na ve Bayes (NB) [31], Genetic Algorithms, Bayesian Network, Decision Trees, Rough Sets, Emerging Patterns, Self-Organizing Maps, have been used by different research for different analysis of microarray gene expression data [32,33]. In classification, available training data sets are generally of a fairly small sample size compared to a large number of genes involved. Theoretically, increasing the size of the genes is expected to provide more discriminating power but in practice, large genes significantly slow down the learning process. As well as cause the classifier to over fit the training data and compromise model simplification. Dimension reduction can be used to successfully extract those genes that directly influence the classification. In this paper, we focus our discussion on popular machine learning techniques for dimension reduction and identification of potentially relevant genes for molecular classification of cancer.
3. Different Dimension Reduction Techniques
For microarray data classification, the main difficulty with most of the machine learning technique is to get trained with a large number of genes. A lot of candidate features (genes) are usually provided to a learning algorithm, for constructing a complete characterization of the classification task. In the past ten years, due to the applications of machine learning or pattern recognition, the domain of features have expanded from tens to hundreds of variables or features used in those applications. Several machine learning techniques are developed to address the problem of reducing irrelevant and redundant features which are a burden for different challenging tasks [34]. The next section is about feature selection methods (filters, wrappers, and embedded techniques) applied on microarray cancer data. Then we will discuss feature extraction methods, special case of feature selection method for microarray cancer data and the final section is about combination of different feature selection method as a hybrid search approach to improve classification accuracy and algorithmic complexity.
3.1. Feature selection
In machine learning, feature selection also known as variable selection, attribute selection or variable subset selection. Feature selection is the process of selecting a subset of relevant and redundant features from a dataset in order to improve the performance of the classification algorithms in terms of accuracy and time to build the model [35]. The process of feature selection is classified into three categories.
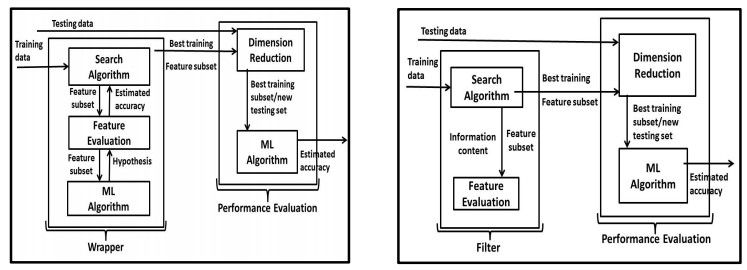
3.1.1. Filter
Filter methods use variable ranking methods as the standard criteria for variable selection by ordering. Statistical ranking methods are used for their simplicity and good success is reported for practical applications. A different suitable ranking criterion of statistics is used to score the variables and select a threshold value in order to remove the variables below it. One definition that can be mentioned, which will be useful for a feature is that "A feature can be regarded as irrelevant if it is conditionally independent of the class labels" [36]. If a feature is to be relevant it can be independent of the input data but cannot be independent of the class labels i.e. the feature that has no influence on the class labels can be discarded [37]. The filter methods grouped in ranking and space search methods according to the strategy utilized to select features [38]. Filter ranking methods select features regardless of the classification model that are based on univariate and multivariate feature ranking techniques. The process of feature selection that follow the filter methods is depicted in Figure 2 [39]. This Figure shows that it selects features, which are similar to ones already picked. This provides a good balance between independence and discrimination. Since the data distribution is unknown, various statistical techniques can be used to evaluate different subsets of features with a chosen classifier. Some of the popular technique found in literature that can be used for feature ranking, with their advantage and disadvantage are listed in Table 1 [40].
Table 1. Advantages and disadvantages of filters methods.
| Model search |
Advantages |
Disadvantages |
Examples |
| Filter |
Univariate |
Fast, Scalable
Independent of the classifier |
Ignores feature dependencies
Some features which as a group have strong discriminatory power but are weak as individual features will be ignored
Features are considered independently |
χ2
Euclidean distance
t-test
Information gain
Gain ratio |
| Multivariate |
The models feature dependencies
Independent of the classifier
Better computational complexity han wrapper methods |
Slower than univariate techniques
Less scalable than univariate techniques
Ignores interaction with the classifier
Redundant features may be included |
Correlation-based feature selection (CFS)
Markov blanket filter (MBF)
Fast correlation-based feature selection (FCBF) |
Different researchers used a different framework of filter methods in their works for the gene selection of microarray data. Lin and Chien, used statistical clustering, based on linear relationship and Coefficient correlation for Breast cancer cDNA micro-array data [41]. Sun et al. utilized local learning based feature selection method for which key idea is to decompose an arbitrarily complex nonlinear problem into a set of locally linear ones through local learning, and then learn feature relevance globally within the large margin framework [42]. Zhu et al. used model-based entropy for feature selection [43]. Some of the researchers used signal-to-noise ratio approach in a leukemia dataset with k-fold and Holdout validation method [44]. Wei et al. developed two recursive feature elimination methods, i.e. Feature score based recursive feature elimination (FS-RFE) and Subset level score based re-cursive feature elimination (SL-RFE) [45]. Liu et al. proposed a novel method to discover differentially expressed genes based on the Robust Principal Component Analysis (RPCA) for the Colon dataset [46]. A prediction scheme was attempted by Maulik and Chakraborty, that combines fuzzy preference based rough set (FPRS) method for feature (gene) selection with semi supervised SVMs [47]. Chinnaswamy A and Srinivasan, advanced a hybrid feature selection approach that combines the correlation coefficient with particle swarm optimization [48]. Recently, a multiphase cooperative game theoretic feature selection approach has been proposed for microarray data classification by Mortazavi et al. in 2016. The average classification accuracy on eleven microarray data sets in this work shows that the proposed method improves both average accuracy and average stability [49].
The benefits of variable ranking is computationally easy and avoids over fitting and is proven to work well for certain datasets. Filter methods do not rely on learning algorithms which are biased and is equivalent to changing data to fit the learning algorithm. One of the drawbacks of ranking methods is that the selected subset might not be optimal because in that a redundant subset might be obtained. Finding a suitable learning algorithm can also become hard since there is no underlying learning algorithm for feature selection [50]. Also, there is no ideal method for choosing the dimension of the feature space [40].
3.1.2. Wrapper methods
Unlike filter methods which use feature relevant criteria, the wrapper methods depend on the performance of classifiers for obtaining a feature subset. Wrapper approach selects the feature subset by using the induction algorithm as a black box (i.e. no knowledge of the algorithm is needed, just the interface is required). The accuracy of the induced classifiers is estimated using accuracy estimation techniques. The main problem of wrapper approach is state space search and different search engines for different method [40]. The different number of search technique can be used to find the best subset of features that maximizes the classification performance, e.g. Branch and Bound method, Genetic Algorithm (GA), Particle Swarm Optimization (PSO). The goal of the search is to find the state with the maximum evaluation, using a trial and error method to guide it. This heuristic approach has a nice property that it forces the accurate estimation to execute cross-validation more times on small datasets than on large datasets [51]. Sequential selection algorithms and Evolutionary search algorithms are two main types of Wrapper methods. The advantage and disadvantage of both the methods are shown in Table 2 with example.
Table 2. Advantages and disadvantages of wrapper methods.
| Model search |
Advantages |
Disadvantages |
Examples |
| Wrapper |
Sequential selection algorithms |
Simple Interacts with the classifier
Small overfitting risk
Less computationally
Prone to local optima
Consider the dependence among features |
Risk of over fitting
More prone than randomized
Algorithms for getting stuck in a local optimum (greedy search)
Classifier dependent methods
The solution is not optimal |
Sequential forward selection (SFS)
Sequential backward elimination (SBE)
Plus q take away r
Beam search |
| Evolutionary selection algorithms |
Less prone to local optima
Interacts with the classifier
Models feature dependencies
Higher performance accuracy than filter |
Computationally intensive
Discriminative power
Lower shorter training times
Classifier dependent selection
Higher risk of over-fitting than deterministic algorithms |
Simulated annealing
Randomized hill climbing
Genetic algorithms
Ant Colony Optimization
Rough set methods
Particle Swarm Optimization
Artificial Bee Colony (ABC) |
a) Sequential selection algorithms
The sequential selection algorithm finds the minimum (or maximum) features by iterating the process. The Sequential Feature Selection (SFS) algorithm starts with an empty set and adds one feature for the first step that increases the performance of the objective function. From the second step onwards the remaining features are added individually to the current subset and the performance of new subset is calculated. By this process the best feature subset can be found that gives the maximum accuracy of the classifier [40]. The process is repeated until the required numbers of features are added. The Sequential Floating Forward Selection (SFFS) algorithm is more flexible than the naive Sequential Floating Selection (SFS) because it introduces an additional backtracking step.
Both the methods SFS and SFFS suffer from generating nested subsets since the forward inclusion is always unconditional which means that two highly correlated features might be included if it gave the highest accuracy in the SFS estimation. A modified Adaptive Sequential Forward Floating Selection (ASFFS) method was developed to avoid the nesting effect [52]. ASFFS method attempted to obtain a less redundant subset than the SFFS algorithm. Theoretically, the ASFFS should produce a better subset of features than the SFFS but this is dependent on the objective function and the properties of the data.
b) Evolutionary selection algorithms
An evolutionary selection algorithm is a method that might not always find the best solution but definitely finds a good solution in reasonable time by sacrificing totality to increase efficiency. The objective of an evolutionary is to produce a solution in a reasonable time frame that is good enough for solving the problem at hand. The Evolutionary search algorithms evaluate different subsets to optimize the performance of the objective function. Different feature subsets are produced either by searching around in a search space or by generating solutions to the optimization problem. Evolutionary algorithms are based on the ideas of biological evolution, such as reproduction, mutation, and recombination, for searching the solution of an optimization problem. The main loop of evolutionary algorithms includes the following steps:
1. Initialize and estimate the initial population.
2. Implement competitive selection.
3. Apply different evolutionary operators to generate new solutions.
4. Estimate solutions in the population.
5. Repeat from the second steps, until some convergence criteria is fulfilled [53].
Some examples of Evolutionary algorithms are Simulated annealing algorithm, Tabu search, Swarm intelligence. The most successful among evolutionary algorithms are Genetic Algorithms (GAs). They have been investigated by John Holland in 1975, and demonstrate essential effectiveness [40]. Wrapper and filter feature selection procedure are depicted in Figure 2.
In 2009 Maugis et al. performed variable selection for cluster analysis with Gaussian mixture models. Here in this study, the model does not need any prior assumptions about the link between the selected and discarded variables [54]. Ai-Jun and Xin-Yuan proposed a Bayesian stochastic feature selection approach for gene selection based on regression coefficients using simulation based Markov chain Monte Carlo methods for Leukemia Colon dataset [55]. Ji et al. presented a novel method named Partial Least Squares (PLS) based gene-selection method [56]. This method is suitable for multicategory classification of microarray data. Sharma et al. proposed the algorithm that first divides genes into a relatively small subset of size h, selects informative smaller subsets of genes (of size r < h) from a subset and merge the chosen genes with another gene subset (of size r) to update the gene subset and repeat this process until all subsets are merged into one informative subset. The effectiveness of the proposed algorithm was shown by analyzing three distinct gene expression data sets and show the relevance of the selected genes in terms of their biological functions [57]. Cadenas et al. proposed an approach, which was based on a Fuzzy Random Forest and it integrates filter and wrapper methods into a sequential search procedure that improved classification accuracy with the selected features [58]. This new method of feature selection can handle both crisp and low quality data. The performance of the filter versus wrapper gene selection technique was evaluated by Srivastava et al. in 2014 by supervised classifiers over three well known public domain datasets with Ovarian Cancer, Lymphomas & Leukemia [59]. In the study, Relief F method was used as a filter based gene selection, and Random gene subset selection algorithm was used as a wrapper based gene selection. Recently, Kar et al. developed a computationally efficient but accurate gene identification technique "A particle swarm optimization based gene identification technique" [60]. In this technique at the onset, the t-test method has been utilized to reduce the dimension of the dataset and then the proposed particle swarm optimization based approach has been employed to find useful genes.
Wrappers tend to perform better, in selecting features because they take the model hypothesis into account by training and testing in the feature space. The main disadvantage of Wrapper methods was the number of iterations required to obtain the best feature subset. For every subset evaluation, the predictor creates a new model, i.e. the predictor was trained for every subset and tested to obtain the classifier accuracy. If the number of samples were large, most of the algorithm execution time was spent in training the predictor. Another drawback of using the classifier performance as the objective function was that the classifiers were prone to overfitting. Overfitting occurs if the classifier model, well learned the data and provides poor generalization capability. The classifier can introduce bias and increases the classification error. Using classification accuracy in feature subset selection, can result in a bad feature subset with high accuracy, but poor generalization power [51].
In the next section, we will discuss embedded methods which try to compensate for the drawbacks in the Filter and Wrapper methods.
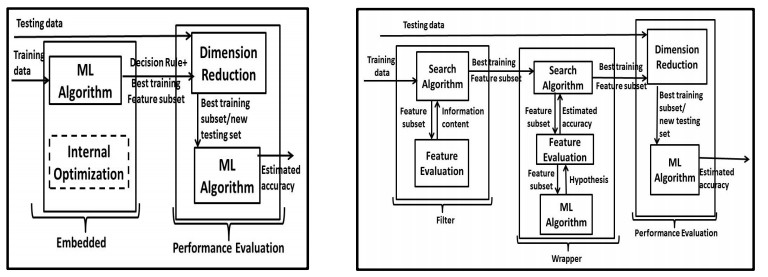
3.1.3. Embedded methods
Embedded methods are different from filter and wrapper in the sense that they still allow interactions with the learning algorithm for feature selection but the computational time is smaller than wrapper methods. An embedded method reduces the computation time taken up for reclassifying different selected subsets in wrapper methods. The main approach of embedded method is to incorporate the feature selection as part of the training process. Embedded methods attempt to compensate, for the disadvantages in the filter and wrapper methods. It considers not only relations between one input features and the output feature, but also searches locally for features that allow better local discrimination [39]. It uses the independent criteria to decide the optimal subsets for a known group. After that, the learning algorithm is used to select the final optimal subset among the optimal subsets of different groups [61]. This embedded method can be roughly categorized into three, namely pruning method, built-in mechanism and regularization models. In the pruning based method, initially all the features are taken into the training process for building the classification model and the features which have less correlation coefficient value are removed recursively using the support vector machine (SVM). In the built-in mechanism-based feature selection method, a part of the training phase of the C4.5 and ID3 supervised learning algorithms are used to select the features. In the regularization method, fitting errors are minimized using the objective functions and the features with near zero regression coefficients are eliminated [40].
Numerous feature selection techniques have been proposed and found wide applications in genomics and proteomics. Niijima and Okuno proposed an unsupervised feature selection method, called LLDA based Recursive Feature Elimination (LLDA-RFE) and applied to several data sets of cancer microarrays. It performs much better than Fisher score for some of the data sets, despite the fact that LLDA-RFE is fully unsupervised [62]. Cai et al. proposed a new L2, 1-norm SVM, to naturally select features for multi-class without bothering further heuristic strategy [63]. Maldonado et al. introduce an embedded method that simultaneously selects relevant features during classifier construction by penalizing each feature's use in the dual formulation of support vector machines (SVM). This approach called kernel-penalized SVM (KP-SVM). It optimizes the shape of an anisotropic RBF Kernel eliminating features that have low relevance for the classifier [64]. Xiang et al. present a framework of discriminative least squares regression (LSR) for multiclass classification and feature selection [65]. Some of the researcher (Liang et al.) integrate multiple data sources and describe the Multi-Source k-Nearest Neighbor (MS-k NN) algorithm for function prediction, which finds k-nearest neighbors of a query protein based on different types of similarity measures and predicts its function by weighted averaging of its neighbors' functions [66]. Cao et al. proposed a novel fast feature selection method based on multiple Support Vector Data Description (SVDD) and applies it to multi-class microarray data [67]. Recursive feature elimination (RFE) scheme with multiple SVDD was introduced to iteratively remove irrelevant features, so the proposed method was called multiple MSVDD-RFE [68]. Recently Miron Bartosz Kursa investigated an idea of incorporating all relevant selections within the training process by producing importance for implicitly generated shadows, attributes irrelevant by design [69]. General properties of embedded algorithm are shown in Table 3.
Table 3. Advantages and disadvantages of embedded methods.
|
Model search
|
Advantages
|
Disadvantages
|
Examples
|
|
Embedded
|
Interacts with the classifier
The models feature dependencies better computational complexity than the wrapper
Higher performance, accuracy than filter
Less prone to over-fitting than wrapper
Preserving data characteristics for interpretability |
Classifier dependent selection
Consider the dependence among features |
Decision trees
Weighted naive Bayes
Feature selection using the weight vector of SVM
Random forests
Least absolute shrinkage and selection
operator (LASSO) |
Feature selection is very popular in the field of microarray data analysis, because of conceptual simplicity. However, it presents two major drawbacks. First, a large part of the information contained in the data set gets lost, since most genes are eliminated by the procedure. Secondly, interactions and correlations between variables are almost always ignored. A few sophisticated procedures try to overcome this problem by selecting optimal subsets with respect to a given criterion instead of filtering out the apparently uninteresting variables. However, these methods generally suffer from over fitting. The obtained variable subsets might be optimal for the learning data set but do not perform nicely on independent test data. Moreover, they are based on computationally intensive iterative algorithms and thus very difficult to implement and interpret.
3.2. Feature extraction
Feature extraction is an intelligent substitute to feature selection to reduce the size of high-dimensional data. In the literature, it is also called "Feature construction" or "projection onto a low dimensional subspace". Feature extraction method transforms the original feature in the lower dimensional space, in this way the problem is represented in a more discriminating (informative) space that makes the further analysis more efficient. There are two main types of feature extraction algorithms, linear and nonlinear. Linear methods are usually faster, more robust and more interpretable than non-linear methods. On the other hand, non-linear methods can sometimes discover for the complicated structures of data (e.g. embedment's) where linear methods fail to distinguish [70].
3.2.1. Linear feature extraction
Linear feature extraction assumes that the data are linearly separable in a lower-dimensional subspace. It transforms them on this subspace by using matrix factorization method. Given a dataset X:N.D, there exists a projection matrix U:D.K and a projection Z:N.K, where Z = X × U. Using UUT = I (orthogonal property of eigenvectors), we get X = Z × UT [71]. The most famous linear feature extraction method is principal component analysis (PCA). PCA uses the covariance matrix and its eigenvalues and eigenvectors, to find the "principal components" in the data that are uncorrelated eigenvectors, each demonstrating some proportion of variance in the data. PCA and its several versions have been applied to reduce the dimensionality of the cancer microarray data. These methods were highly effective in identifying important features of the data. PCA cannot easily capture nonlinear relationship that frequently exists in high dimensional data, especially in complex biological systems, this is the main drawback of PCA [72]. Classical multidimensional scaling (classical MDS) or Principal Coordinates Analysis that estimates the matrix of dissimilarities for any given matrix input are the similar linear approach for data extraction. It was used for high dimensional gene expression datasets because it is effective in combination with Vector Quantization or K-Means that assigns each observation to a class, from the total of K classes [73].
3.2.2. Nonlinear feature extraction
Nonlinear feature extraction works in different ways for dimensionality reduction. In general kernel functions can be considered to create the same effect without using any type of lifting function [71]. Kernel PCA is an important nonlinear method of feature extraction for classification. It has been widely used for biological data. Since, dimensionality reduction helps in the understanding of the results [72]. Nonlinear feature extraction using Manifolds is another similar approach for dimensional reduction. It has been built on the hypothesis that the data (genes of interest) lie on an embedded nonlinear manifold that has lower dimension than the raw data space and lies within it. Many methods exist working in the manifold space and applied to reduce the dimension of microarrays, such as Locally Linear Embedding (LLE) and Laplacian Eigenmaps [74]. Kernel PCA and extraction using manifold methods are widely used feature extraction method for dimension reduction of the microarray. Self-organizing maps (SOM) can also be used for reducing the dimension of gene expression data but it was never generally accepted for analysis. As, it needs just the accurate amount of data to implement well [70]. SOM can often be better separated using manifold LLE but kernel PCA is far faster than the other two. Kernel PCA has an important limitation in terms of space complexity since it stores all the dot products of the training set and therefore, the size of the matrix increases quadratically with the number of data points. Independent component analysis (ICA) is also widely used in microarrays [75]. Independent component analysis (ICA) is a Feature extraction technique, which was proposed by Hyvarinen to solve the typical problem of the non-Gaussian processes and has been applied successfully in different fields. The extraction process of ICA is very similar to the algorithm of PCA. PCA maps the data into another space with the help of principal component. In place of Principal component, the ICA algorithm finds the linear representation of non-Gaussian data so that the extracted components are statistically independent [76,77,78]. ICA finds the correlation among the data and decorrelates the data by maximizing or minimizing the contrast information. This is called "whitening". The whitened matrix is then rotated to minimize the Gaussianity of the projection and in effect retrieve statistically independent data. ICA can also be applied in combination with PCA and combination work better than individuals. This could simply be due to the decrease in computational load caused by the high dimension [78].Popular feature extraction techniques with their properties are shown in Table 4.
Table 4. Advantages and disadvantages of feature extraction methods.
|
Model search
|
Advantages
|
Disadvantages
|
Examples
|
|
Extraction
|
Higher discriminating power
Control over fitting problem |
Loss data interpretability
The transformation may be expensive |
PCA
Linear discriminant analysis
ICA |
Feature extraction control over fitting compared to feature selection when it is unsupervised. Extracted features have the higher discriminating power which gives good classification accuracy. But sometimes data interpretability is lost after transformation and the process of transformation may be costly for a different type of datasets [27].
3.3. Hybrid methods for dimension reduction
Recently, a hybrid search technique has been used for dimension reduction that was proposed by Huang et al. in 2007, that has the advantages of the both filter/extraction and the wrapper method [79]. A hybrid dimension reduction technique consists two stages, in the first step, a filter/extraction method are used to identify best relevant features of the data sets. In the second step, which constitutes a wrapper method, verifies the previously identified relevant feature subsets are verified by a method that gives higher classification accuracy rates [80,81]. It uses different evaluation criteria in different search stages, to improve the efficiency and classification accuracy with better computational performance [21]. In the hybrid search algorithm, the first subset of features is selected or extracted based on the filter/extraction method and after that the wrapper method is used to select the final feature set. Therefore the computational cost of the wrapper method becomes acceptable due to the use of reduced size features [71]. ICA and fuzzy algorithm [76], Information gain and a Memetic algorithm [82], Fishers core with a GA and PSO [83], mRAR with ABC algorithm [84] have recently used the hybrid method to solve the problem of dimensionality reduction of the microarray.Advantages of hybrid methods are listed in Table 5.
Table 5. Advantages and disadvantages of hybrid methods.
|
Model search
|
Advantages
|
Disadvantages
|
|
Hybrid
|
Higher performance, accuracy than filter
Better computational complexity than wrapper
More flexible and robust upon high dimensional data |
Classifier specific methods
Dependents of the combination of different feature selection method |
Minimal redundancy and maximum relevancy (mRMR) is the most popular feature selection method used as a component of the combination with different wrapper methods. For example, Hu et al. applied the search strategy of mRMR for constructing neighborhood mutual information (NMI) for improving the efficiency of mRMR gene selection and to evaluate the relevance between genes and related decision [85]. Akadi et al. propose a two-stage gene selection by combining mRMR as a filter and genetic algorithm (GA) as wrapper [86]. Shreem et al. used Relief F and mRMR as filter stage to minimize redundancy and GA with a classifier to choose the most discriminating genes [87]. Zibakhsh et.al. detected genes using information gain a novel memetic algorithm with a multi-view fitness function [82]. Alshamlan et al. used mRMR-ABC as a hybrid gene selection algorithm for cancer classification of microarray [84]. A hybrid meta-heuristic algorithm called Genetic Bee Colony (GBC) algorithm which combines the advantages of two naturally inspired algorithms: Genetic Algorithm (GA) and Artificial Bee Colony (ABC) is explained by Alshamlan et al. [88]. A complete balance between exploitation and exploration is needed for meta-heuristic population based algorithms. Few modifications are done in the basic ABC and GA algorithm to enhance their abilities. The experiments on various binary and multi class datasets of microarray showed that GBC as a hybrid algorithm selects few genes with high classification accuracy and also when compared with other algorithms like ABC, mRMR-ABC, mRMR-PSO, mRMR-GA, GBC gives better results [39]. A general framework of embedded algorithm and hybrid algorithm are shown in Figure 3.
Chuang et al. proposed to combine Tabu search (TS) and Binary Particle Swarm Optimization (BPSO) for feature selection [89]. BPSO acts as a local optimizer each time the TS have been run for a single generation. The K-nearest neighbor method with leave one out cross validation and support vector machine with one versus rest serve as evaluators of the TS and BPSO. Hybrid genetic algorithms (GA) and artificial neural networks (ANN) are not new in the machine learning culture. Tong and Mintram proposed this method [90]. Such hybrid systems have been shown to be very successful in classification and prediction problems. The widely used k top scoring pair (k-TSP) algorithm is a simple yet powerful parameter free classifier. It owes its success in many cancer microarray data sets to an effective feature selection algorithm that is based on the relative expression ordering of gene pairs. Shi et al. proposed this method in 2011 and is used to predict Cancer outcome [91]. The top scoring pairs generated by the k-TSP ranking algorithm can be used as a dimensionally reduced subspace for other machine learning classifiers. A feature selection method based on sensitivity analysis and the fuzzy Interactive Self Organizing Data Algorithm (ISODATA) is proposed by Liu et al. for selecting features from high dimensional gene expression data sets [92]. Hajiloo et al. introduces fuzzy support vector machine which is a learning algorithm based on the combination of fuzzy classifiers and kernel machines for microarray classification [93]. Chang et al. applied a hybrid of feature selection and machine learning methods in oral cancer prognosis based on the parameters of the correlation of clinicopathologic and genomic markers [94].
To address the drawbacks of each filtering method and wrapper method several hybrid algorithms have been proposed for a microarray data in the literature with suitable results. The Hybrid method gives the best performance for different machine learning classification algorithm than the filter methods and better computational complexity and least prone to overfitting than the wrapper methods. But the performance of hybrid methods are totally dependent on the choice of the classifier, and the combination of the different filter and the wrapper approach.
4. Conclusion
This paper has presented two different ways of reducing the dimensionality of high dimensional microarray data. The first is to select the best features from the original feature set this is called feature selection. On the other hand, feature extraction methods transform the original features into a lower dimensional space by using linear or a nonlinear combination of the original features. To analyze microarray data, dimensionality reduction methods is essential in order to get meaningful results. In this whole paper different aspects feature selection and extraction methods were described and compared. The advantage and disadvantage of these methods are streamlined to get the clear idea about, when to use which method, in order to save computational time and resources. In addition, we have also described a hybrid method that incorporates increasing the classifier accuracy and reducing the computational complexity of an existing method.
Acknowledgement
The author would like to acknowledge the support of the Director, Maulana Azad National Institute of Technology, Bhopal-462003 (M.P.), India, for providing basic facilities in the institute.
Conflict of Interest
All authors declare no conflict of interest.









 DownLoad:
DownLoad: